- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
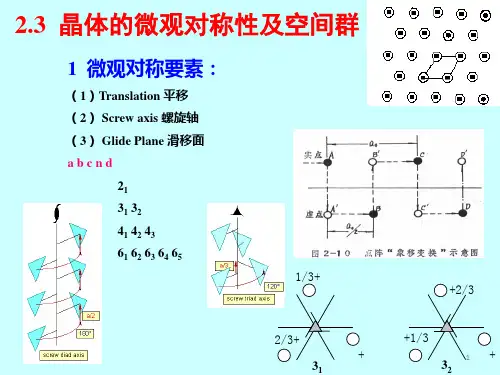
三维晶体的点对称操作通常总可以表示为绕某 一轴的旋转、对某中心的反演和它们的组合. 点对称操作对应的变换矩阵A的具体形式 (1)绕某一轴的旋转(rotation about an axis) 比如:绕x轴的旋转,设转角为θ,则有:
x x y y cos z sin z y sin z cos
x x y y z z
x 1 0 0 x y 0 1 0 y z 0 0 1 z
1 0 0 A 0 1 0 0 0 1
A 1
(3) 镜面反映(Reflection across a plane) 一个镜面反映对称操作(symmetry operation of mirror image)意味着将点阵对应于某一个面进 行反射,点阵保持不变.这表明一系列格点对应于 这个反射面的位臵是等价的,点阵具有镜面反射 对称性.如以xy面为镜面,则(x, y, z) →(x, y, -z)。 用矩阵形式表示,则有
旋转--反演对称轴并不都是独立的基本对称素。
1次旋转反演轴就等价于对称中心i
1 i
2次旋转反演轴就等价于垂直于该轴的对称镜面m
2m
3次旋转反演轴就等价于3次纯旋转轴加上对称中心, 记为 3 3i 3 3i
1i
1 1
2m
1
3 4
5 1
2
2
6
2
6=3+m 3 3 5 1 5 1 6 2 ' 6 4 4 2 A B C D
第三节
晶体的对称性和分类
本节主要内容:
一、晶体的宏观对称性和宏观对称操作
二、晶体的微观对称性和微观对称操作 三、群和晶体结构的分类
一、晶体的宏观对称性和宏观对称操作
物体的性质在不同方向或位臵上有规律地重 复出现的现象称为对称性 对称性的本质是指系统中的一些要素是等 价的,它可使复杂物理现象的描述变得简单、 明了。因为对称性越高的系统,需要独立表征 的系统要素就越少,因而描述起来就越简单, 且能大大简化某些计算工作量。 我们这里要讨论的主要是晶体(晶格或点 阵)的对称性(symmetry of lattice).
2 2 2 2 2 , , , , n 1,6,4,3,2 6 4 3 2
通常把晶体中轴次最高的转动轴称作主对称轴,简 称主轴 (但是立方晶系则以3次轴为主轴),其它为副轴. 晶体的对称操作除了旋转、中心反演和镜面反映3种基 本对称操作外,在某些晶体中还存在着等价于相继进行 两个基本对称操作(乘法)而得到的独立对称操作,称为 组合操作,从而出现新的对称元素 如果一个晶体先绕某轴旋转2π/n,再进行中心反演后, 晶体保持不变,称该轴为n次(或n度)旋转反演轴, 上述操作称为非纯旋转操作。 记为 。n 由于晶体周期性的限制,旋转反演轴也必须遵循晶体 的对称性定律 ,即: n 1, 2, 3, 4, 6
一、晶体的宏观对称性和宏观对称操作
1. 概念解释 晶体的宏观对称性就是晶体外形所包围的点 阵结构的对称性. 晶体的宏观对称性来源于点阵结构的对称性, 相应的宏观对称操作是一种非平移对称操作。 晶体结构可以用布拉维格子或布拉维点阵来描 述,这样以来,晶体变为无限大的空间点阵.从而,晶 体具有了平移对称性,借助于点阵平移矢量,晶格 能够完全复位.我们把考虑平移后的对称性称为 晶体的微观对称性.
0 x 1 y 0 cos z 0 sin x sin y z cos 0
所以,绕x轴旋转的变换矩阵为:
0 1 Ax 0 cos 0 sin sin cos 0
T / T / T T T r r r r ( Ar ) ( Ar ) r A Ar
得证.
/ / / / r ( x , y , z ) Ar ( x, y, z )
T / T / r r r r
以上证明显示,如果晶体在某正交变换下不变, 就称这个正交变换是晶体的一个点对称操作.
x a11 a12 r y A a21 a22 z a 31 a32
a13 a23 a33
x x a11 y y a21 z z a 31
例如立方对称有三条4次轴<100>,绕每个4次轴 旋转π/2、π、3π/2都是对称操作,这样对于三 条4次轴,共有9个对称操作;还有四条3次轴 <111>(空间对角线),绕每个3次轴旋转2π/3、 4π/3都是对称操作,这样对于四条3次轴,共有 8个对称操作;再就是六条2次轴<110>(面对角 线),绕每个2次轴旋转π都是对称操作,这样 对于六条2次轴,共有6个对称操作;不动(旋 转2π)本身也是1个对称操作。所以纯旋转操作 加起来共24个,由于立方对称有对称中心,所 以纯旋转操作加上中心反演的组合操作,即非 纯旋转操作共24个,合起来48个。
6次旋转反演轴等价于3次纯旋转 轴加上垂直于该轴的对称镜面m, 记为 6 3 m
只有具有4次旋转反演轴的晶体,既 没有4次纯旋转轴,也没有对称中心 i,但包括一个与4次旋转反演轴重 合的2次轴.
D
C
A
G
G
H
B F
E H E F 所以旋转反演轴中只有 4 是独立的对称素
旋转反演对称操作中只有4度 旋转反演对称操作是独立的 还有一些其它的组合操作, 如旋转+镜面反映,但不再给 出新的对称元素。
由于把立方体相间的四个顶点连接起来就构 成了正四面体,所以,正四面体所有对称素和 对称操作包含于立方体中。由于正四面体没有 对称中心,立方对称的三条4次轴<100>和对称 中心退化为四次旋转反演轴【6个非纯转动(转 动π/2或3π/2)加上3个纯转动(转动π)】。同 理,四条3次轴<111>和对称中心退化为三次旋 转反演轴(等价于8个纯转动),六条2次轴 <110>和对称中心退化为二次旋转反演轴(6个 非纯转动),加上不动,共24个对称操作。它 保留了立方体的12个纯旋转操作和12个非纯旋 转操作。
A 1
当变换是纯转动时,矩阵的行列式等于+1;当 是空间反演或镜面反射时等于-1. 前一种对应物 体的实际运动,另一种不能靠物体的实际运动 来实现。 3. 宏观对称操作和宏观对称元素 绕固定轴的转动(rotation about an axis)、中 心反演(inversion through a point)和镜面反映 (Reflection across a plane)是晶体中的三种基本 的点对称操作。相应的对称元素有:对称轴、对 称中心、对称面。
晶体的对称性可以从晶体外形的规则性上反映 出来,如sc、bcc、fcc结构的立方晶体,绕晶胞的任 一基矢轴旋转π/2或π/2的整数倍的操作,都能使晶 体的外形保持不变,这就是晶体的对称性.
操作前后晶体保持自身重合的操作,称为对称 操作. 晶体借以进行对称操作的轴、平面或点.称为对 称元素(简称对称素). 这种对称性不仅表现在晶体的几何外形上,而且 反映在晶体的宏观物理性质中,称为晶体的宏观 对称性.
a12 a22 a32
a13 x a23 y a33 z
A为变换矩阵,由于点对称操作不改变两点间的 距离,所以易证A是一个正交矩阵.亦即满足
A A E
T
两点间的距离不变,即 用矩阵表示即
x 2 y 2 z 2 x2 y2 z2
写成矩阵形式,则有
x x a11 y y a21 z z a 31 a12 a22 a32 a13 x a23 y a33
x x y y z z
x 1 0 0 x y 0 1 0 y z 0 0 1 z
1 0 0 A 0 1 0 0 0 1
同理可得绕y轴和绕z轴的变换矩阵
cos Ay 0 sin 0 sin 1 0 0 cos
cos Az sin 0
sin cos 0
0 0 1
且矩阵行列式均为:
A 1
(2)中心反演(inversion through a point) 如果,晶体有对称中心,则中心反演也是对称操 作. 对原点的反演使得 (x, y, z) → (-x, -y, -z),即:
还有一套标记法,是固体物理中惯用的标记, 是熊夫利(Schoenflies)制订的,因此称为熊夫利 符号(Schoenflies notation). 熊夫利符号中Cn 表 示旋转轴;Sn 表示旋转反演轴;Ci 表示中心反 演;Cs 表示镜面反映。
晶体中8种独立的宏观对称元素(或对称操作) 用熊夫利符号标记则为C1,C2,C3,C4,C6 ,Ci, Cs,S4。 总之,晶体的所有点对称操作都可由这8种操 作或它们的组合来完成。
由于晶体的宏观对称操作不包含平移,所以宏 观对称操作时,晶体至少保持有一个点不动,相应 的对称操作又称为点对称操作. 2. 对称操作的变换矩阵
从数学角度来看,晶体的点对称操作实质上是对 晶体进行一定的几何变换,它使得晶体中的某一 / / / / 点 r ( x, y, z ) r ( x , y , z ) Ar ( x, y, z )
由于 ABAB 组成等腰梯形,
因此 m为整数
AB mAB ma,
B
a
A
a
亦即: 2a cos( ) a ma