晶体结构的对称性解读

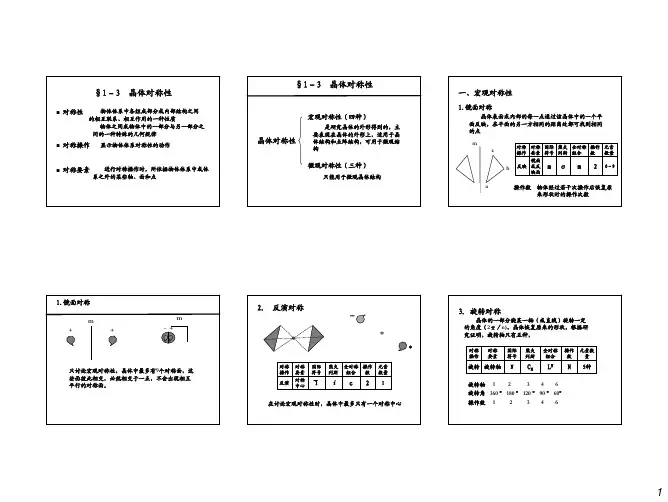
晶体对称性晶体对称性是晶体学研究的一个重要组成部分，它是晶体结构的关键，可以解释晶体的外观、性质以及界面问题。

其中，最常见的是空间群，它用数学表示法确定变换的形式。

接下来，让我们来更多地了解晶体对称性：一、空间群1. 什么是空间群：空间群是一种变换群，也是对称性理论的基础，可以描述物体在特定坐标系中的集合子空间上的空间操作。

举个例子，如果一个物体只可以在空间系中做180°旋转，那么它就只具有一种（即旋转）拓扑群。

2. 空间群划分：空间群可以根据对称性来划分，主要包括有限对称群、无限对称群和单调对称群三类。

其中，有限对称群表示法子群的形状、大小或空间构造不变；无限对称群指的是无限种变换，其轴心、空间点或空间构造不变；而单调的对称群是单一的元素组成的，在该空间群中任何对称性都不变。

二、对称性1. 什么是对称性：对称性是空间群的基础，一般来说，它表示物体在某种坐标下有特定形状和空间操作的属性，也可以用数学表示法来表达这种特征。

2. 对称性的类型：对称性的类型可以分为四大类，分别是正交对称性、立体对称性、平面对称性和点对称性。

其中，正交对称性主要涉及空间中的空间坐标变换，立体对称性是指物体在立体坐标系下的操作，而平面对称性是指物体在平面坐标系下的操作，而点对称性则是指物体在特定空间构造下的操作。

三、晶体对称性1. 晶体对称性是什么：晶体对称性是晶体学研究的一个重要组成部分，它涉及到晶体结构的外观、性质以及界面问题的解释。

2. 晶体对称性的应用：晶体对称性可以用来研究和设计多种材料，如金属、半导体、有机分子晶体、生物晶体等，它们是将材料化学性质同物理性质关联起来，从而更好地理解材料的特性。

此外，晶体对称性也可用于分类、指导结构分析以及材料的设计和合成等。

四、总结从上文可以看出，晶体对称性是一个非常重要的概念，它不仅仅可以用来描述物体的形状、大小和空间结构，而且可以应用于许多不同的领域，如材料的研究与设计等。

晶体学中的晶体对称性与晶体结构研究简介晶体学是自然科学中一门研究晶体结构和性质的学科。

晶体的对称性和结构是晶体学的重要内容。

晶体学的研究不仅有基础研究价值，还有着广泛的应用价值。

本文将从晶体对称性角度出发，探讨晶体结构研究的方法和应用。

晶体对称性晶体对称性是指晶体内部各部分具有相同的排列规律和几何形状。

在晶体学中，对称性是衡量晶体完美度的重要指标之一。

晶体对称性有两种：点对称性和空间对称性。

点对称性是指在晶体中存在一个点，经过该点进行旋转、镜像后，晶体的内部结构与原来完全相同。

空间对称性是指晶体在三维空间中存在对称操作，包括：旋转、镜像和反演。

常见的点对称性包括：• 二重轴对称性：具有一个旋转轴，使得晶体绕该轴旋转180°之后，晶体内部结构不变。

• 旋转对称性：具有一个旋转轴，使得晶体绕该轴旋转360/n，n为正整数，晶体内部结构不变。

• 镜像对称性：具有一个镜面，可以将晶体分为两个相等的部分，其中一部分镜像另一部分。

• 反演对称性：把晶体的每个点关于一个特定点反转，即点P 关于点O反演以后的点P'在O点所连的向量上，并且OP'=OP。

常见的空间对称性包括：• 立方晶系：八面体对称性，有三个互相垂直的二重对称轴和四个三重对称轴。

• 正六角柱晶系：具有六重对称轴和三个对面对称面。

• 单斜晶系：具有垂直于晶面的二重对称轴和平行于晶面的镜面对称性。

• 菱面体晶系：具有正四面体对称性和八面体对称性。

晶体结构研究晶体结构研究是晶体学的重要组成部分，其目的是通过测定晶体结构，揭示其性质和物理、化学等科学规律，从而为新材料开发和新制备方法提供依据。

测定晶体结构需要使用X射线衍射和电子衍射等技术。

现代技术使得晶体结构的测定更加快速、精确。

应用晶体学的应用范围很广，包括：• 材料科学：晶体学为材料科学领域提供了重要手段，例如材料的研究、优化和制备。

• 生物科技：晶体学技术为生物分子结构研究提供了关键信息，如解决蛋白质三维结构、探寻酶催化机理等。