当前位置：文档之家 › 1.2 晶格及其平移对称性

1.2 晶格及其平移对称性

  • 格式：ppt
  • 大小：11.03 MB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

晶体对称性

晶体对称性
6次反轴为3次轴加对称面
准 晶
晶体中只有1， 2，3，4，6 次旋转轴，没有 5次轴和大于6 次以上的轴，可 以直观的从只有正方形、长方形、正三角形、正六边形可以重复布满平面， 而 5 边形和 n (>6)边形不能布满平面空间来直观理解。因此固体中不可能存 在 5 次轴曾是大家的共识，然而1984年美国科学家Shechtman在急冷的铝 锰合金中发现了晶体学中禁戒的 20 面体具有的 5 次对称性，这是对传统晶 体观念的一次冲击。
晶体的宏观对称性的描述
原子的周期性排列形成晶格，不同的晶格表现出不同 的宏观对称性 概括晶体宏观对称性的方法是考察晶体在正交变换的 不变性 三维情况下，正交变换的表示:
x x ' a11 y y ' a 12 z z' a 13
−1 ������ = 0 0
0 0 −1 0 0 −1
0 0 −1
1 0 ������(������������) = 0 1 0 0 1 0 ������ = 0 1 0 0 0 0 1
像转操作(Rotary reflection):
������������������������ ������ ������ = ������������������������ 0
目前普遍的认识是：晶体的必要条件是其 构成原子的长程有序，而不是平移对称性， 具有 5 次对称性的准晶体(Quasicrystal) 就是属于原子有严格的位置有序，而无平 移对称性的晶体。它的图像可从二维 Penrose拼图中得到理解。实际是一种准 周期结构，是介于周期晶体和非晶玻璃之 间的一种新的物质形态—准晶态。
(3). 底心单斜
C2 , Cs , C2 h

12晶格及其平移对称性.

12晶格及其平移对称性.
School of Physics, Northwest University
Solid State Physics
1. 简单立方晶体结构（simple cubic structure; sc）
把晶格设想成原子球的规则堆积，在一个平面内的最简单的堆积便是正 方排列，如下图所示，任一个原子球与同一平面内的四个最近邻相切。如 果把这样的原子层叠起来，各层的球完全对应，就形成所谓的简立方结构。 用黑原点代表原子球就得到简立方的结构单元。
—— 体心立方晶格 结构的金属 Li、Na、K Rb、Cs、Fe
School of Physics, Northwest University
Solid State Physics
体心立方晶格结构金属 —— Iron
School of Physics, Northwest University
Solid State Physics
3、密堆积结构晶体
简立方和体心立方结构都不是原子球最紧密的堆积方式。 原子球如果要构成最紧密的排列，每一个原子球都必须与同平面 内相邻的6个原子球相切。原子球在一个平面内最紧密的排列方式， 称为密排面。把密排面叠起来可以形成原子最紧密堆积的晶格。
要形成密堆积，只要把一 层的球心对准另一层的球 隙即可。
一、 晶体结构及基元（crystal structure and basis）
（一）常见的晶体结构 晶体中原子的具体排列形式称为晶体结构。 不同晶体原子规则排列的具体形式如果是不同的，则它们具有不同的晶
体结构； 若晶体的原子排列形式相同，只是原子间的距离不同，则它们具有相同
的晶体结构。 下面是常见的几种晶体结构：
Solid State Physics
§1.2 晶格及其平移对称性（lattice and translation symmetry）

固体物理晶体结构12晶格基本类型

固体物理晶体结构12晶格基本类型

20
固体物理导论
第 1 章 晶体结构
1.2 晶格的基本类型
3. 正交
abc a b 90
c
ba a b
布拉维格子： 1. 简单正交 2. 底心正交 3. 体心正交 4. 面心正交
21
固体物理导论
第 1 章 晶体结构
1.2 晶格的基本类型
4. 四方
abc a b 90
6. 三角
abc
a b 120 , 90
布拉维格子：三角
c
b ab a
24
固体物理导论
7. 六角
第 1 章 晶体结构
1.2 晶格的基本类型
abc a b 90 , 120
布拉维格子：六角
c
b ab a
25
固体物理导论
第 1 章 晶体结构
B′
于纸面的轴旋转a角度为
aa
对称操作 C → C′
A
B
C
D
根据格点的等价性，绕通过C点垂直于纸面 的轴旋转-a角度也为对称操作 B → B′
BC // B′C′
B′C′ = m BC, m∈ Z
B′C′ = BC[1+2cos(p-a)]
2
固体物理导论
第 1 章 晶体结构
1.2 晶格的基本类型
m BC= BC[1+2cos(p-a)] cosa = (1-m)/2
11
固体物理导论
第 1 章 晶体结构
1.2 晶格的基本类型
7. 只包含旋转反演轴的点群，标记为Sn 群，但 S1=Ci， S2=Cs， S3=C3h，只有S4，S6群，共2个
8. 立方对称的48个对称操作称为立方点群，用 Oh标记；正四面体的24个对称操作，称为正四 面体群，用Td 标记。共2个

1-晶体结构及其对称性(研)

1-晶体结构及其对称性(研)
A 原子的右侧一定距 离处有一个碳原子而左 侧没有，但是B 原子则 相反。
二维蜂窝格子 (非布拉菲格子)
如果将A、B两个原子看作为一 个基元，则点阵结构就如前页所示 ，格子就是布拉菲格子了。
14种布拉菲格子:
1.简单三斜； 2.简单单斜， 3.底心单斜； 4.简单正交， 5.底心正交， 6.体心正交， 7.面心正交； 8.六角； 9.三角； 10.简单四方， 11.体心四方； 12.简单立方， 13.体心立方， 14.面心立方。
（3）金刚石结构（ diamond ）：
碳的同素异构体。 经琢磨后的金刚石又称钻石。 无色透明、有光泽、折光力极强，最硬的物质。
金刚石结构是复式晶格结构，基元中有两个碳原子A、B， 布拉菲格子是面心立方。
或可视为两个面心立方子晶格，沿体对角线平移1/4 体对角 线长度套构而成，如图所示．
金刚石晶体的配位数是4, 这4个碳原子构成一个 正四面体，碳-碳键角为109º28´。
例如，简立方晶格的几个晶面表示。
注意：晶向指数与晶面指数的表示差异。
晶向指数表示晶列取向，用中括号[…]表示； 晶面指数表示晶面方向，用圆括号(…)表示。
§1.3 倒格子
一、定义
晶体的布拉菲点阵由三个原胞基矢 、a1 、a2 来a描3 述．
定义三个新矢量：
b1
2
(,a2
其中： a1 轴[100]， a2 轴[010]， a3 轴[001]，
a1 轴 [1 00] 等，其中－1的负号放在1的上面。
二、晶面和晶面指数
任意三个不共线的格点，构成一个晶面．
与晶列性质类似，晶面也具有下面三个方面的性质： 任一晶面上都有无穷多个格点； 任一晶面都有无穷多个互相平行的晶面，构成一个晶面簇； 每一个晶面簇都将晶体中所有的格点包含无遗．

晶体的结构及其对称性

晶体的结构及其对称性
配位数：8
原子半径：
r
3
V
atom
4 3 a 3 4
3 a 4
V
bcc

a
3
Body centered cubic lattice
原子数： 堆积密度：
8
1 1 2 8
atom
f V
2
V

bcc
3 8
具有此结构的金属原子：碱金属Li、Na、K、Rb、Cs；难熔金 属W、Mo、Nb、Ta等。
的平移对称性。
• 基元按点阵排布得到晶体结构： <点阵>+<基元>=<晶体结构>
三、基矢和元胞 对于一个给定的点阵，总可以选择三个不共面的基本平移矢量������1 、������2 、������3
（称为点阵的基矢），使任意一个结点
3
������������ =������1 ������������ +������2 ������������ +������3 ������������ =
关于常见晶体结构的一些定义： • 配位数：每个原子周围的最近邻原子数 • 堆积密度：原子球的体积与其所占据的有效空间体积之比
（1）简单立方(sc)晶体结构
配位数：6
a
3
原子半径： r 2
V
atom
4 3
a 2
V
原子数： 堆积密度：
sc

a
3
Simple cubic lattice
• 面心立方(fcc)晶体结构
配位数：12
原子半径：
r
3
4 2 V fcc V atom 3 4 a 1 1 8 6 4 原子数： 8 2

第一章 晶体的对称性

第一章 晶体的对称性

第一章晶体的对称性§1-1 晶体内部结构的周期性---点阵与晶格大家都知道晶体内部原子(分子、离子和原子团等，以后称质点)的排列是规则的，具有一定的周期性，这是晶体的主要特点。

不同晶体中的质点在空间中的排列规律是不同的，有许多种排列方式。

因此，在对晶体进行研究时，为了归类方便，常将构成晶体的实际质点抽象成纯粹的几何点，并称之为阵点。

这样的阵点在空间中周期性规则排列并有相同的周围环境。

这种阵点的空间排列就称为空间点阵，或晶体点阵，也称布拉法格子，简称点阵或晶格，共有14种。

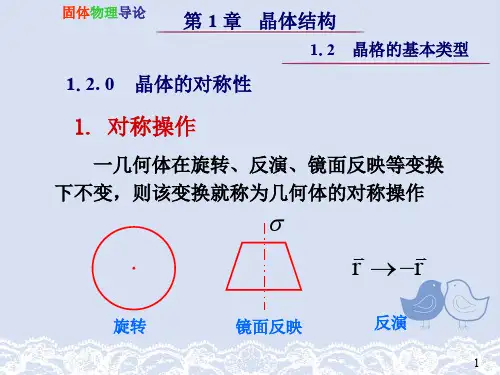
§1-2 晶体的宏观对称性---点对称操作晶体内部结构不仅具有周期性，还具有比较复杂的对称性。

实际上，晶体宏观性质和外形的对称性都是其内部结构对称性的反映，与其有着密切关系。

应该说，人们最初认识晶体，是从它们丰富多彩又有规则的外部形状开始的，后来才逐步认识到，晶体外形上的规则性及其宏观性质的对称性，是与其内部微观结构的对称性密切相关的。

在本节及以下几节中，通过对晶体的宏观对称性的描述，引进群的初步概念，给出晶体的32个点群，并依据晶体对称性特征，区分晶类和晶系。

1．晶体的宏观对称性。

晶体外形上（宏观上）的规律性，突出表现在晶面的对称排列上。

如：把立方体的岩盐晶体绕其中心轴每转900后，晶体自身就会重合，而把六面柱体的石英晶体绕其柱轴每转600后，晶体亦会自身重合。

这里提到的绕轴转动称旋转操作，是一种点对称操作。

通常把经过某种点对称操作后晶体自身重合的性质称为晶体的宏观对称性。

描述晶体宏观对称性的方法，就是列举使其自身重合的所有点对称操作。

为了明确对称性和对称操作的概念，先给出以下概念：●相等图形。

如花瓣。

●等同图形。

如左右手。

相等图形属于等同图形，但等同图形不一定是相等图形。

●对称图形。

由两个或两个以上的等同图形构成的并在空间有规律排列的图形称对称图形。

2．对称性。

对称图形中各等同部分在空间排列的特殊规律性称对称性。

晶体结构的对称性晶体结构的对称性

晶体结构的对称性晶体结构的对称性

v， w为整数
r = (ua + vb +wc) + (xa + yb +zc)
x, y, z是在晶胞之内指定一个位置的分数座标。 x, y, z用晶胞边长的分数表示，在0-1之间变化。晶胞原点的 分数坐标总是0，0，0。 用相同分数座标x、y和z指定
的所有位置都对称等价。（由于晶体的三维周期性，在分
(2)旋转轴(旋转轴) ：绕某轴反时针旋转 =360/n度， n称为 旋转轴的次数(或重数)，符号为n (Cn)。其变换矩阵为：
cos
sin 0
sin 0 cos 0 0 1
晶体结构的对称性-董成
旋转矩阵
x2 x1 cos
y1 sin
y2 y1 cos x1 sin sin 0 x1 x2 cos y sin cos 0 y 2 1 0 1 0 z2 z1 sin 0 cos sin cos 0 Rz, ( ) 0 1 0
晶体结构的对称性-董成
练习题
1.
证明：(1)倒反中心是一次反轴;(2)镜面是 二次反轴。 找出一个立方体具有的所有旋转轴。(6个2 次轴， 4个3次轴， 3个4次轴。)
2.
晶体结构的对称性-董成
非点式对称操作
非点式对称操作：是由点式操作与平移操作 复合后形成的新的对称操作，平移和旋转复 合形成能导出螺旋旋转，平移和反映复合能 导出滑移反映。
晶体结构的对称性-董成
晶体性质
晶体是原子(包括离子，原子团)在三维空间中 周期性排列形成的固体物质。晶体有以下的共同性 质： 1. 均匀性; 2. 各向异性; 3. 自范性; • 对称性; • 稳定性。

1.2晶格的基本类型

1.2晶格的基本类型

X ( x1, x2 , x3 ) X ( x1, x2 , x3 )
x2
O点和X点间距与O点和 X点间距相等。
x12 x22 x32 x1 2 x2 2 x3 2
X~ X A~X~ AX X~A~AX X~X
A~A I
I为单位矩阵，即：IΒιβλιοθήκη 1 0 00 1 0
100
或者说A为正交矩阵，其矩阵行列式A 1 。
如果考虑平移，还有两种情况，即螺旋轴和滑移反映面。
（5）n度螺旋轴：若绕轴旋转2/n角以后，再沿轴方向平 移l(T/n)，晶体能自身重合，则称此轴为n度螺旋轴。其中T是 轴方向的周期， l是小于n的整数。 n只能取1、2、3、4、6。
（6）滑移反映面：若经过某面 进行镜象操作后，再沿平行于该面 的某个方向平移T/n后，晶体能自 身重合，则称此面为滑移反映面。 T是平行方向的周期， n可取2或4。
C1，C2，C3，C4，C6 （用熊夫利符号表示）
(2)旋转反演对称操作： 1，2，3，4，6度旋转反演对称操作。 S1，S2，S3，S4，S6（用熊夫利符号表示）
(3)中心反映：i。
(4)镜象反映：m。
独立的对称操作有8种,即1，2，3，4，6，i，m， 4 。
或C1，C2，C3，C4，C6 ，Ci，Cs，S4。
x1 x2 x3
1 0 0
0
cos sin
0
sin cos
x1 x2 x3
A
1 0 0
0
cos sin
0
sin cos
A 1
晶体中允许有几度旋转对称轴呢?
设B1ABA1是晶体中某一晶 面上的一个晶列，AB为这一晶 列上相邻的两个格点。
B

1.2对称性和布拉维格子的分类

1.2对称性和布拉维格子的分类

见黄昆书30页
20面体的 对称性
目前普遍的认识是：晶体的必要条件是其构成原子的 长程有序，而不是平移对称性，具有 5 次对称性的 准晶体（Quasicrystal）就是属于原子有严格的位置 有序，而无平移对称性的晶体。它的图像可从二维 Penrose拼图中得 到理解。实际是一
种准周期结构，是 介于周期晶体和非 晶玻璃之间的一种 新的物质形态—— 准晶态 。
1.2
对称性和布拉维格子的分类
一. 对称性的概念 二. 晶体中允许的对称操作 三. 晶体宏观对称性的表述：点群 四. 七个晶系和14种晶体点阵 五. 晶体的微观对称性：空间群 六. 点群对称性和晶体的物理性质
除去晶体点阵外，晶体的结构还能够用什么样 的语言方便地描述?
一.对称性的概念：
一个物体（或图形）具有对称性，是指该物 体（或图形）是由两个或两个以上的部分组成， 经过一定的空间操作（线性变换），各部分调换 位置之后整个物体（或图形）保持不变的性质。 对称操作：维持整个物体不变而进行的操作称作对 称操作。即：操作前后物体任意两点间的距离保 持不变的操作。 点对称操作：在对称操作过程中至少有一点保持不动 的操作。有限大小的物体，只能有点对称操作。 对称元素：对称操作过程中保持不变的几何要素： 点，反演中心；线，旋转轴；面，反映面等。
其中 Aij 为正交矩阵 从解析几何知道，符合正交 变换的是：绕固定轴的转动 (Rotation about an axis) 绕 z 轴旋转θ 角
a11 s r Ai j a21 a 31 a12 a22 a32 a13 a23 a33
sin cos 0 0 0 1
通过仔细分析可知正四面体允许的对称操作只有 24个；正六角拄的对称操作也只有24个，它们都没有 立方体的对称性高。

固体物理课件第二章_晶体的结构

固体物理课件第二章_晶体的结构



Na+构成面心立方格子 Cl－也构成面心立方格子
(6) CsCl: 由两个简单立方子晶格彼此沿 立方体空间对角线位移1／2 的长度套构而成
(7) 闪锌矿结构
化合物半导体 —— 锑化铟、砷化镓、磷化铟 面心立方的嵌套
（8） 钙钛矿结构
钛酸钙（CaTiO3） 钛酸钡（BaTiO3） 锆酸铅（PbZrO3） 铌酸锂（LiNbO3） 钽酸锂（LiTaO3）等
面心立方格子:原点和12个近邻格点连线的垂 直平分面围成的正十二面体
体心立方格子:原点和8个近邻格点连线的垂直 平分面围成的正八面体，沿立方轴的6个次近 邻格点连线的垂直平分面割去八面体的六个角， 形成的14面体 —— 八个面是正六边形，六个面是正四边形
§1.2 晶列和晶面
思考： 金刚石为什么有固定的面？ 这些面和晶格结构有什么关系？
根据周期性：
f e
k k
ikx
fk e
k
ik ( x na )
f k eikx f k eik( x na)
k k
e
ik na
1
m 0,1,2,
k na k Rn 2m
2 k h Gh a
k=b的波传过一个晶格长度，相位改变2π
晶面：所有结点可以看成分布在一系列相互平 行等距的平面族上，每个平面族称为一个晶面 晶面用法向或晶面指数标志
例：同一个格子，两组不同的晶面族
晶面的性质： –晶格中一族的晶面不仅平行，并且等距 –一族晶面必包含了所有格点 –三个基矢末端的格点必分别落在该族的不 同晶面上（有理指数定理）
晶面（米勒）指数：晶面把基矢 a1 , a2 , a3 分别

固体物理 1.2_晶格的基本类型

固体物理 1.2_晶格的基本类型

所属点群
四方 三角 六角 立方
简单四方 体心四方
三角
六角
简单立方 体心立方 面心立方
a=b c
a= b ＝= 90º
a=b=c
a= b ＝ 90º
C4、S4、C4h、D4 C4V、D2d、D4h
C3、S6、D3 C3Ｖ、D3d
a=b c
C6、C3h、C6h、D6、
a= b ＝ 90º, =120º C6V、D3h、D6h
第 1 章 晶体结构
1.2 晶格的基本类型
立方体的对称操作
对称操作 对称操作数
不动
1
6个2度轴
6
总的对称操作数：
4个3度轴
8
24+24=48
3个4度轴
9
旋转反演
24
15
第 1 章 晶体结构
1.2 晶格的基本类型
正四面体的对称操作
对称操作 对称操作数
不动
1
3个2度轴
3
4个3度轴
8
总旋转操作数 1+3+8=12
第 1 章 晶体结构
1.2 晶格的基本类型
点阵（或晶体）中的对称元素：
（ａ）转动轴： 1、2、3、4、6
（ｂ）转动反演： 4
（ｃ）对称心：
ｉ
（ｄ）镜面：
ｍ
一种点阵可以同时存在若干种对称元素。对称操作的一种特 定的组合方式叫做点群。点群在“群论”中有严格的定义 ，点群代表的是点阵或晶体的对称性，也就是点阵或晶体 能进行什么样的对称操作。
第 1 章 晶体结构
1.2 晶格的基本类型
对称操作通常包括两大类： 平移对称操作
点对称操作
第 1 章 晶体结构

L2-晶体结构与对称性2PPT课件

L2-晶体结构与对称性2PPT课件
不同的元素。
许多重要的半导体化合物都是闪锌矿结构。
.
8
4、六角密积结构
其结构图见P343习题10的图。 由化学键的取向不同可知，体内原子与六方形 顶角的原子是不等价的。所以六角密积是有两个六 角布喇菲晶格套构而成。六角形底面的边长为a，晶 胞高度为c。
.
9
固体物理学原胞 120见0角下，图a。3 沿原垂胞直基密矢排a1面、的a方2 在向密。排基矢面表内达，式互见成 P342第五题。
晶体。
.
11
晶向:
同族晶列中的晶列相互平行，并且完全等同，所 以一族晶列的特点是晶列的取向。晶列的取向称 为晶向。
晶向的表示法
对应于一个简约格矢量
R l1 a 1 l2 a 2 l3 a 3
(
l1
、l 2
、l 3
为互质整数）
晶向记为 [ l1 ，l 2 ，l 3 ]。
[ l1 ，l 2 ，l 3 ] 称为晶列指数。
1、氯化钠结构 由两个面心立方格子套构而成。 具有氯化钠结构的化合物有： LiF、LiCl、NaF、CaO等。
.
3
2、氯化铯结构
由两个简单立方格子套构而成。
具有氯化铯结构的化合物有： CsBr、CsI、TlCl、TlI、TLBr等。
.
4
3、金刚石结构 金刚石由碳原子组成，其晶胞见P19图1-13。
h
于是 , (r Rl ) ( K h )eiK h r eiK h Rl
h
(r Rl ) (r )要求 eiK h Rl 1
常用密勒指数表示不同的晶面系。
.
16
密勒指数的确定
选一格点为原点，以原胞基矢a1、a2、a3 为轴线；
由于所有格点都在晶面系上，所以必然有一晶面通 过原点，其它晶面均匀切割各轴；

材料设计—5-晶格及其平移对称性

材料设计—5-晶格及其平移对称性

基元
无论是简单还是复式晶格，都可以找到一个最小 的、完全等价的结构单元，一个理想晶体，通过 这个单元在空间无限周期重复排列而得到。这个 单元称为基元，它可以含有一个或者多个原子。 任何两个基元中的原子排列完全相同。 比如NaCl结构中，虽然Na,Cl不等价，从Na平移到 Cl不能够实现晶体不变。但如果把Na, Cl两个原子 看做一个整体单元，那么这个单元通过平移就可 以保持晶体不变。
到二十世纪，Hilbert认为Kepler猜想十分重要从而把它收入到他 的二十世纪23个最重要的待解决的问题中。 直到二十世纪末，Michigan大学教授Thomas Hales花费了十年的 时间，终于通过计算机解决了这个问题。
实际上，晶体中原子的空间排列类似于小球 的堆积问题。区别在于原子有很多种类型， 而且原子之间的相互作用非常复杂，所以原 子排列也是十分复杂的。原子排列不一定遵 循密堆积形式，而是要保持所得的晶体结构 能量最低。
பைடு நூலகம்


fcc点阵
面心立方以顶点为原点，到其近邻的三个面 心为基矢。立方体的边长为a。
a a1 jk 2 a a2 ik 2 a a3 i j 2
a1
a2


a3
1 3 Ω a1 a 2 a 3 a 4


初基元胞的特点：
初基元胞基矢往往不垂直，由它所构成的初 级元胞往往不能直观反映出点阵的宏观对称 性。但它完全反映出点阵的平移对称性。
准晶：介于晶体和非晶之间，虽然原子分布完全 有序，但无周期性，仅仅具有长程取向序。可以 有晶体所不允许的旋转对称性。
平移周期性
一个结构平移之后能够完全复原：
固体中的原子都是摩尔量级的，那么如何来研究这么多的 原子呢？

1.2 晶体结构(对称性 倒空间)

1.2 晶体结构(对称性 倒空间)

School of Physics and Information Technology, SNNU
晶体对称操作
1. 旋转对称性(Rotational Symmetry) 和对称操作：晶格围绕一固定 轴(二维：通过格点而且垂直平面；三维：晶向(Direction))转动角 度或以后，晶格保持不变。 2. 有限的平移对称性(Translational symmetry)：有限制的平移对 称操作是指平移任意的分立的矢量(discretized vectors ) Rl=l1al+l2a2+l3a3。 3.反映( symmetry plane) 和对称操作：晶格对一晶面(Lattice Plane)反射(二维：对通过格点的线进行反射)，晶格不变。
13立方2
School of Physics and Information Technology, SNNU
正四面体的对称操作
—— 金刚石晶格（Fd3m） 四个原子位于正四面体的四个顶 角上，正四面体的对称操作包含
在立方体操作之中
1) 绕三个立方轴转动 —— 共有3个对称操作
Diamond
School of Physics and Information Technology, SNNU
School of Physics and Information Technology, SNNU
230 种空间群 space groups
空间群：由点群对称操作和平移对称操作组合而成；由 32 晶体 学点群与 14个Bravais 点阵组合而成； 空间群是一个单胞（包含单胞带心）的平移对称操作；反射、旋 转和旋转反演等点群对称性操作、以及螺旋轴和滑移面对称性操作 的组合。 晶体学中的空间群是三维周期性物体(晶体)变换成它自身的对称 操作(平移，点操作以及这两者的组合)的集合。一共有230种空间 群。 每种空间群唯一的对应一种晶体结构。自然界的晶体结构只能 有230种。 230 空间群符号 = Bravais点阵类型符号 + 点群对称元素

晶体的对称性与空间群

晶体的对称性与空间群

晶体的对称性与空间群3.1 晶格与非晶态物质不同，晶体中分子、离子或原子团在空间按照一定的规律排列而形成的固体物质。

也就是说，在晶体内部，分子、离子或原子团在三维空间以某种结构基元（structural motif）(即重复单位)的形式周期性的排列。

只要知道其中最简单的结构基元，以及他们在空间平移（translation）的向量长度与方向，就可以得到原子或者分子在晶体中的排部的情况。

结构基元可以是一个或者多个原子（离子），也可以是一个或者多个原子（离子），也可以是一个或者多个分子，每个结构基元的化学组成及原子的空间排列完全相同。

如果将结构基元抽象为一个点，晶体中分子或原子的排列就可以看成点阵（lattice）。

也就是说，晶体的结构=结构基元+点阵。

单晶体都属于三维点阵，为了直观，这里采用简化的二维点阵来说明。

图 3.1（a）显示[Cu2(ophen)2]分子[1]在晶胞中二维平面上的排列，其中每个结构基元一个[Cu2(ophen)2]分子，可以抽象为一个点阵点，从而形成一个点阵，如图3.1（b）所示。

显然，每个点阵点按在空间排列而成的平面，点阵的单位向量平移，就与另一个点阵点（即分子）完全重叠。

可以用三个互相不平行的单位向量a, b 和c描述点阵点在空间的平移，通过这个向量的操作，可以得到整个点阵。

点阵中任意点可以用向量r表示。

r=n1a+n2b+n3c(3.1)其中n1, n2和n3为整数。

点阵是抽象的数学概念，其原点可以任意选定。

需要指出的是，晶体学上的坐标系均采用右手定则，即食指代表x轴，中指代表y轴，大拇指代表z轴。

3.1.1晶胞参数晶体的空间点阵可以选择三个互相不平行的单位向量a，b和c，用它们可以画出一个六面体单位，称为点阵单位。

相应地，按照晶体结构的周期性所划分的六面体单位就叫晶胞（cell）.三个单位向量的长度a,b和c以及它们之间的夹角α，β，γ就叫晶胞参数（unit cell parameters）其中，α是b和c的夹角，β是a和c的夹角，γ是a和b的夹角（图3.2）。

高二物理竞赛课件：分立对称性 晶格平移

高二物理竞赛课件：分立对称性 晶格平移
取θ=ka，则
u k (x a) u k (x)
Bloch定理 x eikxuk (x),
u k (x a) u k (x)
可见晶格平移的本征态|θ>之波函数可写成平面波 与具有晶格周期性的函数之乘：
k (x) eikxuk (x), u k (x a) u k (x)
且 k a a , a，k空间范围称为（第一）
由于
,求和局限于相关态
注意：[V,Lz]=0, 电场不破坏轴对称,m仍是好量子数
取|R>~|S>+|A>，|L>~|S>-|A>,在π作用下|R>和 |L>对调. |R>和|L>不是π的本征态，也不是H的本 征态，但有相同能量期待值. |R>和|L>是非定态, 若t0=0处于|R>，则t时状态为
Bloch定理 有限高势垒时，|n>并不完全局域于格点n，而是
主要集中于格点n而随与n的距离而衰减。 以|n>为基构造|θ>，|θ>仍为本征值为e-iθ的本征态
由于 x (a) x a x ei ,
设 x eikxuk (x), x a e u ik(x-a) k (x a)
非紧束缚：能带概念相似，形状复杂些 多电子、多原子晶胞：不同能带可交叉
小结： 含时势、相互作用绘景 H=H0+V(t),
态矢方程(耦合微分方程组)
例：电场中的球对称原子
忽略自旋自由度，并设体系不简并（V不改变态的自 旋），则据微扰理论，能量变化为
无微扰态是宇称本征态，zkk=0, 无线性Stark效应（体 系无电偶极矩）。故微扰产生的是2阶Stark效应。
若 , , , 1,
则 x 0,除非 ，即奇宇称的x
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

c.p layers are oriented perpendicular to the body diagonal of the cube
School of Physics, Northwest University
Solid State Physics
4
金刚石结构（diamond
金刚石晶体由碳原子组成，其
School of Physics, Northwest University
Solid State Physics
下面是几种常见的实际晶体结构：
5、氯化钠型结构 (sodium chloride structure): 氯化钠晶格是由纳离子和 氯离子相间排列构成的。钠离 子（○）和氯离子（●）各自 构成一面心立方格子，彼此之 间沿立方边位移立方边的一半 穿套而成，也就是说，氯化钠 晶体是两种不同离子各自构成 的面心立方子晶格套构形成的。 除了NaCl之外，所有碱金属卤 化物晶体，如LiF、KCl、LiI等 都具有NaCl晶体结构。
hcp
A closed-packed structure is created by placing a layer of spheres B on top of identical close-packed layer of spheres A. There are two choices for a third layer. It can go in over A or over C. If it goes in over A the sequence is ABABAB. . . and the structure is hcp. If the third layer goes in over C the sequence is ABCABCABC. . . and the structure is fcc.
Solid State Physics
§1.2 晶格及其平移对称性（lattice and translation symmetry）
一、晶体结构及基元（crystal structure and basis） （一）常见的晶体结构（common crystal structures） （二）基元和晶体结构（basis and crystal structure） （三）简单格子和复式格子（simple and compound lattice ） 二、原胞和基矢（primitive cell and primitive translation vectors） （一）原胞和基矢 （二）晶胞或惯用原胞(unit cell and conventional unit cell) （三）Wigner-Seitz原胞 ( Wigner-Seitz primitive cell ) 三、常见晶体结构的原胞和晶胞 （primitive cell and unit cell of common crystal structures ） （一）简立方（simple cubic） （二）体心立方（body-centered cubic） （三）面心立方（face-centered cubic） 四、配位数和致密度 本节思路：首先给出常见的晶体结构，然后从晶格的周期性出发，介绍布拉菲 格子、原胞、晶胞、等概念。
体心立方晶格的堆积方式
体心立方晶格的典型单元
School of Physics, Northwest University
Solid State Physics
体心立方晶格
体心立方晶格结构 原子球排列形式
体心立方原子球排列方式表示 —— AB AB AB ……
School of Physics, Northwest University
School of Physics, st University
Solid State Physics
§1.2 晶格及其平移对称性（lattice and translation symmetry）
一、 晶体结构及基元（crystal structure and basis）
（一）常见的晶体结构 晶体中原子的具体排列形式称为晶体结构。 不同晶体原子规则排列的具体形式如果是不同的，则它们具有不同的晶 体结构；
School of Physics, Northwest University
Solid State Physics
Packing
Can pack with irregular shapes
School of Physics, Northwest University
Solid State Physics
体心立方晶格结构金属 —— Iron
School of Physics, Northwest University
Solid State Physics
3、密堆积结构晶体
简立方和体心立方结构都不是原子球最紧密的堆积方式。 原子球如果要构成最紧密的排列，每一个原子球都必须与同平 面内相邻的6个原子球相切。原子球在一个平面内最紧密的排列方 式，称为密排面。把密排面叠起来可以形成原子最紧密堆积的晶格。
金刚石晶格结构的典型单元
成。
School of Physics, Northwest University
Solid State Physics
金刚石晶格结构
—— 碳原子构成的一个面心立方原胞内还有四个原子 分别位于四个空间对角线的 1／4处
—— 一个碳原子和其它四个碳 原子构成一个正四面体
—— 金刚石结构的半导体晶体 Ge、Si等
Can stack close packed (c.p.) to give 3D structures？
School of Physics, Northwest University
Solid State Physics
最紧密的堆积可以形成两种不同最紧密的晶格排列——六角密排和立方密排。 在堆积时，如果第二层密排面上的原子球的球心对准前一层的球隙，第三层的 原子球心对准第二层的球隙并和第一层的原子球心一一对准，典型的结构单元 如图所示,这样的得到晶格，称为六角密排晶格（hexagonal close-packed； hcp）。
2、体心立方晶体结构（body-centered cubic struture；bcc）
如果把简立方堆积的原子球均匀地散开一些，在原子球的空隙内放一个全 同的原子球，使空隙内的原子球与最近邻的8个原子球相切，便构成了体心立方 结构。下图分别是体心立方的堆积方式和结构单元。 体心立方晶格结构的晶体，除了在立方体的顶角位置各有一个原子以外， 在体心位置还有一个原子，体对角线的长度等于两个原子球的直径。
Solid State Physics
体心立方晶格中，A层中原子球的距离等于 A－A层之间的 距离，A层原子球的间隙 —— —— 原子球的半径 —— 体心立方晶格 结构的金属 Li、Na、K Rb、Cs、Fe
School of Physics, Northwest University
Solid State Physics
六角密排（hexagonal close packing; ABAB…）
六角密排晶格的典型结构单元
School of Physics, Northwest University
Solid State Physics
原子球排列 —— AB AB AB ……
六角密排晶格结构晶体 Be、Mg、Zn、Cd 铍、 镁、 锌、 镉
School of Physics, Northwest University
Solid State Physics
ccp = fcc ?
Add construction lines - can see fcc unit cell
Build up ccp layers (ABC… packing)
立方密排 (cubic close packing； ABCABC…）
面心立方晶格的典型单元
School of Physics, Northwest University
Solid State Physics
面心立方晶格
B层原子球排列
C层原子球排列
School of Physics, Northwest University
原子球的正方排列 简单立方晶格的典型单元 School of Physics, Northwest University
Solid State Physics
用圆点表示原子的位置 —— 得到简单立方晶格结构
School of Physics, Northwest University
Solid State Physics
NaCl晶格结构的典型单元
School of Physics, Northwest University
Solid State Physics
氯化钠由Na+和Cl－结合而成 —— 一种典型的离子晶体
Na+构成面心立方格子；Cl－也构成面心立方格子
School of Physics, Northwest University
要形成密堆积，只要把一 层的球心对准另一层的球 隙即可。
密堆积 School of Physics, Northwest University
Solid State Physics
Close packed structures
Most efficient way of packing equal sized spheres. In 2D, have close packed layers Coordination number (CN) = 6. This is the maximum possible for 2D packing.
School of Physics, Northwest University