固态电子论-第三章习题参考解答
- 格式:pptx
- 大小:436.87 KB
- 文档页数:23



错误率比较低的题目1、 材料按电性能分为哪三类?电阻率范围是多少?导体:cm ⋅Ω<-410ρ;绝缘体:cm ⋅Ω>610ρ;半导体:cm ⋅Ω=-6410~10ρ 2、 如何控制材料的导电性能?对于金属和半导体材料哪种因素更重要,解释原因 控制材料的导电性能实际上就是控制材料中的载流子的数量和这些载流子的移动速率。
对于金属材料来说,载流子的移动速率特别重要.对于半导体材料来说,载流子的数量更为重要。
载流子的移动速率取决于原子之间的结合键、晶体点阵的完整性、微结构以及离子化合物中的扩散速率。
3、 禁带宽度的概念电子填满的价带与未被电子填充的空带(导带)间没有交叠,价带和导带间被禁带隔开,禁带宽度V C g E E E -=4、 反应材料导电性能好坏的2个参数电阻率ρ和电导率σ σρ/1=5、 杂质半导体中,多子数量和少子数量分别与什么因素有关在杂质半导体中多子的数量与掺杂浓度有关。
在杂质半导体中少子的数量与温度有关。
6、 本征激发的概念价电子在获得一定能量(温度升高或受光照)后,即可挣脱原子核的束缚,成为自由电子(带负电),同时共价键中留下一个空位,称为空穴(带正电)。
这一现象称为本征激发。
7、 为什么Si 是半导体基石?从能带结构来看碳、硅、锗导电性差距大的原因 锗比硅容易提纯,所以最初发明的半导体三极管是锗制成的。
但是,锗的禁带宽度(0.67eV )只有硅的禁带宽度(1.11eV )的大约一半,所以硅的电阻率比锗大,而且在较宽的禁带中能够更加有效地设置杂质能级,所以后来硅半导体逐渐取代了锗半导体。
硅取代锗的另一个主要原因是在硅的表面能够形成一层极薄的SiO2绝缘膜,从而能够制备MOS 型三极管。
虽然锗、硅和锡的能带结构与金刚石相似,但这些材料的禁带宽度Eg 较小。
实际上,锡的禁带宽度小得使它具有类似导体的导电性。
而禁带宽度Eg 稍大一点的锗和硅成了典型的半导体。
禁带宽度:C 金刚石(5.48eV )、Si (0.67eV )、Ge (0.08eV )8、 能带结构中,电子和空穴的运动方向9、 外加电压的作用下,P 型半导体和N 型半导体的主要电流,区分两种半导体的方法P 型半导体是空穴电流,n 型半导体是电子电流。



固体物理习题一、 固体电子论基础1. 已知金属铯的E F =1.55eV ,求每立方厘米的铯晶体中所含的平均电子数。
(提示:常温下F E 与0F E 相差不大,可以令0F F E E ≈)解:因为常温下费米能级E F 与绝对零度时的费米能级E F 0相差不大,可令E F ≈E F 0。
金属中的电子可近似地按自由电子气处理,在E ~E+dE 能量区间内的电子态数(计及自旋)为:()dE CE dE E hm VdZ 212132324==π其中:()2132324E hm VC π=, V 为金属的体积,m 为电子的质量。
由于电子遵循费米分布,于是在能量区间E ~E+dE 中的电子数为: dE E E Cf dZ E f dN )()(==式中)(E f 是费米分布函数。
由于在绝对零度时有:⎪⎩⎪⎨⎧><=)E (E 0)E (E 1)(0F 0FE f因此电子总数为:2332300)2(38)(32)(0F FE mE h VE C dEE C dE E E Cf N Fπ====⎰⎰∞单位体积内的电子数为: 233)2(38F mE hV Nn π==代入有关数据得到: )(108.7 )106.155.1101.92()1063.6(314.38321231228327----⨯≈⨯⨯⨯⨯⨯⨯⨯⨯⨯=cm n2. 证明:在T=0K 时,费米能级0F E 处的能态密度为:0023)(FF EN E N =,式中N为金属中的自由电子数。
证明:在K 空间中,在周期性边界条件下,以K K =为半径的球内,电子的数目为(记及自旋):3342K V n π⋅=因此:dK K V dn 28π⋅= (1) 已知自由电子的能量为:mK h E 222=,代入(1)式得:d E E hm Vd n 21323)2(4π= (2)因此电子按照能量分布的状态密度:21323)2(4)(E hm Vd E d nE N π==(3)当T=0K 时,全部电子处于费米球内。

第一章 金属自由电子气体模型习题及答案1. 你是如何理解绝对零度时和常温下电子的平均动能十分相近这一点的?[解答] 自由电子论只考虑电子的动能。
在绝对零度时,金属中的自由(价)电子,分布在费米能级及其以下的能级上,即分布在一个费米球内。
在常温下,费米球内部离费米面远的状态全被电子占据,这些电子从格波获取的能量不足以使其跃迁到费米面附近或以外的空状态上,能够发生能态跃迁的仅是费米面附近的少数电子,而绝大多数电子的能态不会改变。
也就是说,常温下电子的平均动能与绝对零度时的平均动能十分相近。
2. 晶体膨胀时,费米能级如何变化?[解答] 费米能级3/222)3(2πn mE o F= , 其中n 单位体积内的价电子数目。
晶体膨胀时,体积变大,电子数目不变,n 变小,费密能级降低。
3. 为什么温度升高,费米能反而降低?[解答] 当K T 0≠时,有一半量子态被电子所占据的能级即是费米能级。
除了晶体膨胀引起费米能级降低外,温度升高,费米面附近的电子从格波获取的能量就越大,跃迁到费米面以外的电子就越多,原来有一半量子态被电子所占据的能级上的电子就少于一半,有一半量子态被电子所占据的能级必定降低,也就是说,温度生高,费米能反而降低。
4. 为什么价电子的浓度越大,价电子的平均动能就越大?[解答] 由于绝对零度时和常温下电子的平均动能十分相近,我们讨论绝对零度时电子的平均动能与电子的浓度的关系。
价电子的浓度越大,价电子的平均动能就越大,这是金属中的价电子遵从费米—狄拉克统计分布的必然结果。
在绝对零度时,电子不可能都处于最低能级上,而是在费米球中均匀分布。
由式3/120)3(πn k F =可知,价电子的浓度越大费米球的半径就越大,高能量的电子就越多,价电子的平均动能就越大。
这一点从3/2220)3(2πn m E F=和3/222)3(10353πn mE E oF ==式看得更清楚。
电子的平均动能E 正比于费米能o F E ,而费米能又正比于电子浓度32l n。



福州大学至诚学院《固体电子学》试卷答案(一)一、单项选择(每题 2 分,共10 分)1.电子在晶体中的共有化运动指的是 C 。
A.电子在晶体中各处出现的几率相同B.电于在晶体原胞中各点出现的几率相同C. 电子在晶体各原胞对应点出现的几率相同D.电子在晶体各原胞对应点有相同位相2.离子晶体可能的最大配位数是 B 。
A.12 B.8 C.6 D.43.根据费米分布函数,电子占据(E F + kT)能级的几率 B 。
A.等于空穴占据(E F + kT)能级的几率 B. 等于空穴占据(E F-kT)能级的几率C.大于电子占据E F的几率D.大于空穴占据E F的几率4.下列说法中错误的是 A 。
A.特鲁德模型,即量子的自由电子气模型,是建立在金属电子气体假设基础上的。
B. 在特鲁德模型中,认为金属电子气体是玻色子,遵循玻尔兹曼统计规律。
C.在索末菲模型中,认为金属电子气体是费米子,遵循费米统计规律。
D. 特鲁德对金属结构的基本描述是金属原子由原子实和价电子两部分构成。
5.对于只含一种杂质的非简并n型半导体,费米能级E F随温度上升而 D 。
A.单调上升 B. 单调下降C.经过一极小值趋近E F D.经过一极大值趋近E F二、填空(每空 2 分,共20 分)1.氯化钠结构复式格子可以看作是由两个面心立方结构子晶格套构而成。
2.电子亲和能一般随着原子半径的减小而增大。
3.由正负离子相间排列的一维离子链的马德隆常数是2ln2 。
4.B原子在Si晶体中形成的是p型半导体,P原子在Si晶体中形成的是n型半导体。
5.原子电负性=0.18(电离能+ 电子亲和能),用它来作为一种元素的原子对外层电子吸引能力的衡量尺度。
6.两种不同金属接触后,费米能级高的金属带正电,对导电有贡献的是费米面附近位置的电子。
7.我们一般采用回旋共振实验来测量有效质量。
三、简答题(每题8分,共24分)1.从能带论的角度解释为什么导体,半导体和绝缘体的导电能力存在差别;半导体与导体,半导体与绝缘体的最大区别在哪里?答:满带和空带不导电,半满带才导电。
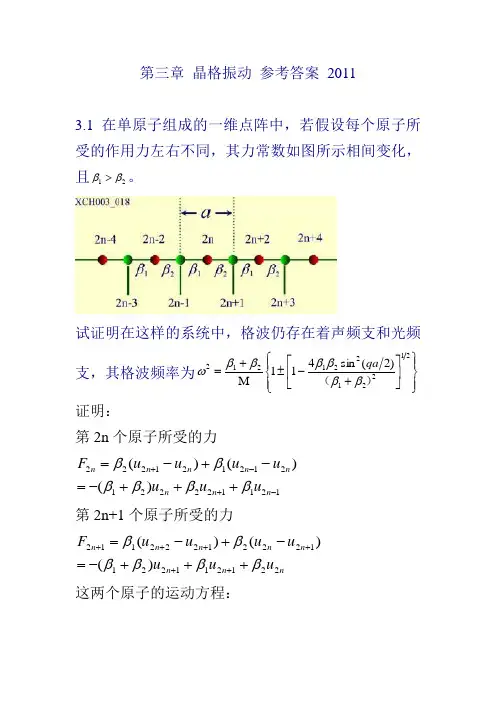
第三章 晶格振动 参考答案 20113.1 在单原子组成的一维点阵中,若假设每个原子所受的作用力左右不同,其力常数如图所示相间变化,且21ββ>。
试证明在这样的系统中,格波仍存在着声频支和光频支,其格波频率为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=21221221212)2(sin 411M )(ββββββωqa 证明:第2n 个原子所受的力121122221212121222)()()(-+-++++-=-+-=n n n n n n n n u u u u u u u F ββββββ第2n+1个原子所受的力nn n n n n n n u u u u u u u F 22121122112221222112)()()(ββββββ+++-=-+-=++++++这两个原子的运动方程:n n n n n n n n u u u um u u u um 221211221121211222212)()(ββββββββ+++-=+++-=+++-+方程的解⎥⎦⎤⎢⎣⎡+-+⎥⎦⎤⎢⎣⎡-==q a n t i n q a n t i n Beu Aeu 2)12(122)2(2ωω代入到运动方程,可以得到B A e e B m A B e e A m q a i q a i q ai q a i )()(21222122122212ββββωββββω+-⎪⎪⎭⎫ ⎝⎛+=-+-⎪⎪⎭⎫ ⎝⎛+=--- 经整理,有0)(0)(22122212221221=-+-⎪⎪⎭⎫ ⎝⎛+=⎪⎪⎭⎫ ⎝⎛+--+--B m A e e B e e A m q a i q a i q ai q a i ωββββββωββ 若A ,B 有非零解,系数行列式满足,.,22122212221221=-+++-+--ωββββββωββm eeeem q a i q ai q a i q a i根据上式,有⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡+-±+=21221221212)2(sin 411M )(ββββββωqa3.2具有两维正方点阵的某简单晶格,设原子质量为M ,晶格常量为a ,最近邻原子间相互作用的恢复力常数为β,假定原子垂直于点阵平面作横振动,试证明此二维系统的格波色散关系为)(a q a q y x cos cos 22M 2--=βω。
固体物理课后习题解答(黄昆版)第三章黄昆固体物理习题解答第三章晶格振动与晶体的热学性质3.1 已知⼀维单原⼦链,其中第j个格波,在第个格点引起的位移为,µ= anj j sin(ωj_j+ σj) ,σj为任意个相位因⼦,并已知在较⾼温度下每个格波的平均能量为,具体计算每个原⼦的平⽅平均位移。
解:任意⼀个原⼦的位移是所有格波引起的位移的叠加,即µn= ∑ µnj=∑ a j sin(ωj t naq j+σj)j j(1)µ2 n =∑µjnj∑µj*nj=µj2nj+ µ µnj*nj′j j′由于µ µnj?nj数⽬⾮常⼤的数量级,⽽且取正或取负⼏率相等,因此上式得第2 项与第⼀项µ相⽐是⼀⼩量,可以忽略不计。
所以2= ∑ µ 2njn j由于µnj是时间的周期性函数,其长时间平均等于⼀个周期内的时间平均值为µ 2 = 1 T∫0 2 ω+σ 1 2 j aj sin( t naqjj j)dt a=j(2)T0 2已知较⾼温度下的每个格波的能量为KT,µnj的动能时间平均值为1 L T ?1 ?dµ 2 ?ρw a2 T 1= ∫∫dx0?ρnj?= j j∫0 2 ω+ σ= ρ 2 2 T??dt L a sin( t naq)dt w Lanj T0 0 0 ? 2 ?dt??2T0 j j j j 4 j j其中L 是原⼦链的长度,ρ使质量密度,T0为周期。
1221所以Tnj= ρ w La j j=KT(3)4 2µKT因此将此式代⼊(2)式有nj2 = ρωL 2 jµ所以每个原⼦的平均位移为2== ∑ µ 2= ∑KT= KT∑1n njρωL2ρLω2j j j j j3.2 讨论N 个原胞的⼀维双原⼦链(相邻原⼦间距为a),其2N 格波解,当M=m 时与⼀维单原⼦链的结果⼀⼀对应.解答(初稿)作者季正华- 1 -黄昆固体物理习题解答解:如上图所⽰,质量为M 的原⼦位于2n-1,2n+1,2n+3 ……质量为m 的原⼦位于2n,2n+2,2n+4 ……⽜顿运动⽅程:..mµ2n= ?βµ(22n?µ2n+1 ?µ2n?1)..Mµ2n+1 = ?βµ(22n+1 ?µ2n+2 ?µ2n)体系为N 个原胞,则有2N 个独⽴的⽅程i na q⽅程解的形式:iµ2n=Ae[ωt?(2 ) ] µ2n+1=Be[ω?(2n+1)aq]na qµ=将µ2n=Ae[ωt?(2 ) ]2n+1 Be i[ωt?(2n+1) aq]代回到运动⽅程得到若A、B 有⾮零的解,系数⾏列式满⾜:两种不同的格波的⾊散关系:——第⼀布⾥渊区解答(初稿)作者季正华- 2 -第⼀布⾥渊区允许 q 的数⽬黄昆固体物理习题解答对应⼀个 q 有两⽀格波:⼀⽀声学波和⼀⽀光学波。
第四章 固体电子论 参考答案1. 导出二维自由电子气的能态密度。
解:二维情形,自由电子的能量是:22222()()22x y k E k k mm==+k2πLx xk n =,2πLy yk n =在/k =到d k k +区间:22222d 2d 2π(2π)2ππS Lm L Z kdk dE=⋅=⋅=k那么:2d ()d Z Sg E E=其中:22()πm g E =2. 若二维电子气的面密度为n s ,证明它的化学势为:2π()ln exp 1s B B n T k T m k T μ⎡⎤⎛⎫=-⎢⎥⎪⎝⎭⎣⎦解:由前一题已经求得能态密度:22()πm g E =电子气体的化学势μ由下式决定:()()222E-/E-/01d ()d πe1e1B B k Tk TL mE N g E LE μμ∞∞==++⎰⎰令()/B E k Txμ-≡,并注意到:2s Nn L =()12/1d πB xB s k Tk T mn exμ-∞-=+⎰()2/d π1B x B xxk Tk Tm e ee μ∞-=+⎰2/lnπ1BxB xk Tk T m ee μ∞-=+()/2ln 1πB k TB k T m eμ=+那么可以求出μ:2π()ln exp 1s B B n T k T m k T μ⎡⎤⎛⎫=-⎢⎥⎪⎝⎭⎣⎦证毕。
3. He 3是费米子,液体He 3在绝对零度附近的密度为0.081 g /cm 3。
计算它的费米能E F 和费米温度T F 。
解:He 3的数密度:N N M N n V M VMmρρ==⋅=⋅=其中m 是单个He 3粒子的质量。
()1123233π3πF k n m ρ⎛⎫== ⎪⎝⎭可得:2222322/33π(3)22F E n mm m ρπ⎛⎫== ⎪⎝⎭代入数据,可以算得: E F =6.8x 10-16erg = 4.3x 10-4eV .则:FF E T k ==4.97 K.4.已知银的密度为310.5/g cm ,当温度从绝对零度升到室温(300K )时,银金属中电子的费米能变化多少?解:银的原子量为108,密度为310.5/g cm ,如果1个银原子贡献一个自由电子,1摩尔物质包含有6.022x 1023个原子,则单位体积内银的自由电子数为2232310.55.910()108/6.02210n cmmρ-===⨯⨯在T=0K 时,费米能量为202/3328FhnEm π=()代如相关数据得2/3272227302812(6.6310)()3 5.910()29.110()8 3.148.8710() 5.54()Ferg s cmEg erg eV -----⎛⎫⨯⋅⨯⨯=⎪⨯⨯⨯⎝⎭≈⨯≈在≠T0K时,费米能量2020]12B F FFK TE E E π=[1-()所以,当温度从绝对零度升到室温(300K )时, 费米能变化为202012B F FFk TE E E π-=-()代如相关数据得4F FE E -⨯⨯-⨯≈⨯≈2-162-12-163.14(1.3810300)=-128.8710-1.610(erg)-10(eV )可见,温度改变时,费米能量的改变是微不足道的。
第三章 材料的性能 1.用固体能带理论说明什么是导体,半导体,绝缘体? 答:固体的导电性能由其能带结构决定。
对一价金属(如Na ),价带是未满带,故能导电。
对二价金属(如Mg ),价带是满带,但禁带宽度为零,价带与较高的空带相交叠,满带中的电子能占据空带,因而也能导电。
绝缘体和半导体的能带结构相似,价带为满带,价带与空带间存在禁带。
禁带宽度较小时(0.1—3eV )呈现半导体性质,禁带宽度较大(>5eV )则为绝缘体。
答案或者是: 满带:充满电子的能带 空带:部分充满或全空的能带 价带:价电子填充的能带 禁带:导带及满带之间的空隙 (其中,空带和价带是 导带) 导体:价带未满,或价带全满但禁带宽度为零,此时,电子能够很容易的实现价带与导带之间的跃迁。
半导体:价带全满,禁带宽度在0.1-3eV 之间,此时,电子可以通过吸收能量而实现跃迁。
绝缘体:价带全满,禁带宽度大于5eV ,此时,电子很难通过吸收能量而实现跃迁 2、 有一根长为5 m ,直径为3mm 的铝线,已知铝的弹性模量为70Gpa ,求在200N 的拉力作用下,此线的总长度。
= 5.002 m 3.试解释为何铝材不易生锈,而铁则较易生锈? 答:锈蚀机理不同,前者为化学腐蚀,后者为电化学腐蚀铝是一种较活泼的金属,但因为在空气中能很快生成致密的氧化铝薄膜,所以在空气中是非常稳定的。
铁与空气中的水蒸气,酸性气体接触,与自身的氧化物之间形成了腐蚀电池,遭到了电化学腐蚀,所以容易生锈。
4.为什么碱式滴定管不采用玻璃活塞?答:因为普通的无机玻璃主要含二氧化硅,二氧化硅是一种酸性的氧化物,在碱液中将会被溶解或侵蚀,其反应为:SiO2+2NaOH →Na2SiO3+H2O5.何种结构的材料具有高硬度?如何提高金属材料的硬度?答:由共价键结合的材料具有很高的硬度,这是因为共价键的强度较高。
无机非金属材料由离子键和共价键构成,这两种键的强度均较高,所以一般都有较高硬度,特别是当含有价态较高而半径较小的离子时,所形成的离子键强度较0/F A σ= (H E σε=00()/l l lε=-()/l l l ε=-高(因静电引力较大),故材料的硬度较高。