人教版五年级下从课本到奥数长方体和正方体1-1
- 格式:doc
- 大小:449.50 KB
- 文档页数:4



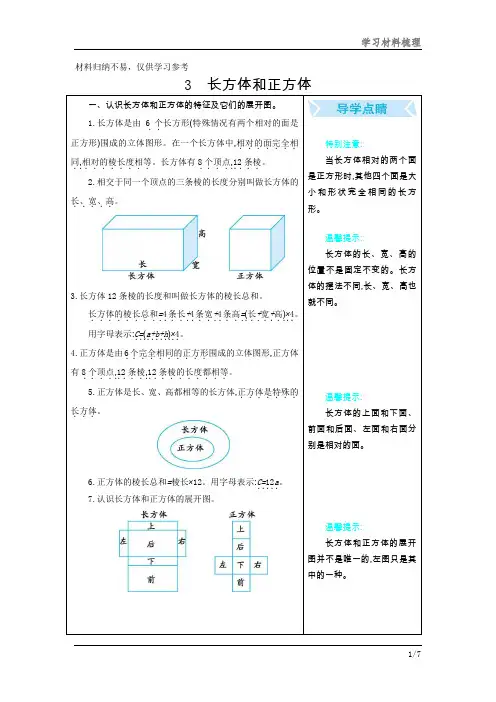
材料归纳不易,仅供学习参考3 长方体和正方体一、认识长方体和正方体的特征及它们的展开图。
1.长方体是由6.个.长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
在一个长方体中,相对的面完全相.......同.,.相对的棱长度相等........。
长方体有8.个顶点...,.12..条棱..。
2.相交于同一个顶点的三条棱的长度分别叫做长方体的长、宽、高.....。
3.长方体12条棱的长度和叫做长方体的棱长总和。
长方体的棱长总和........=.4.条长..+.4.条宽..+.4.条高..=.(.长.+.宽.+.高.).×.4.。
用字母表示:C=..(.a+b+h.....).×.4.。
4.正方体是由6.个完全相同的正方形.........围成的立体图形,正方体有8.个顶点...,.12..条棱..,.12..条棱的长度都相等........。
5.正方体是长、宽、高都相等的长方体,正方体是特殊的.......长方体...。
6.正方体的棱长总和=棱长×12。
用字母表示:C=..12..a.。
7.认识长方体和正方体的展开图。
特别注意:当长方体相对的两个面是正方形时,其他四个面是大小和形状完全相同的长方形。
温馨提示:长方体的长、宽、高的位置不是固定不变的。
长方体的摆法不同,长、宽、高也就不同。
温馨提示:长方体的上面和下面、前面和后面、左面和右面分别是相对的面。
温馨提示:长方体和正方体的展开图并不是唯一的,左图只是其中的一种。
无底又无盖长方体表面积=(长×高+宽×高)×2S=2(ah+bh)贴墙纸正方体的表面积=棱长×棱长×6 S=a×a×6用字母表示:S= 6a2生活实际:油箱、罐头盒等都是6个面游泳池、鱼缸等都只有5个面水管、烟囱等都只有4个面。
注意1:用刀分开物体时,每分一次增加两个面。
(表面积相应增加)注意2:长方体或正方体的长、宽、高同时扩大几倍,表面积会扩大倍数的平方倍。

⼈教版五年级下从课本到奥数长⽅体和正⽅体1-1电⼦教案长⽅体和正⽅体1.⼀个长⽅体棱长总和是60厘⽶,已知长是宽的1.5倍,宽是⾼的2倍,求这个长⽅体的长、宽、⾼.2.⼀个长⽅体棱长总和是96厘⽶,已知长是宽的1.5倍,宽是⾼的2倍,求这个长⽅体的长、宽、⾼.3.⼀个长⽅体棱长总和是103.2厘⽶,已知长是宽的1.2倍,宽是⾼的1.5倍,求这个长⽅体的长、宽、⾼.4.⼀个正⽅体的棱长总和是93.6厘⽶,它的棱长是多少?5.⼀个长25厘⽶、宽20厘⽶、⾼18厘⽶的长⽅体盒⼦,如果按如图所⽰的虚线⽤绳⼦捆起来,不计接头处绳⼦的长度,需要多长的绳⼦?(5)(6)(7)6.⼀个长2.2⽶、宽1.8⽶、⾼2⽶的长⽅体⽊箱,按如图所⽰的虚线⽤绳⼦捆起来,不计接头处绳⼦的长度,需要多长的绳⼦?7.⼀个棱长6分⽶的正⽅体物品,按如图所⽰的虚线⽤绳⼦捆起来,接头处是40厘⽶,那么⾄少需要多长的绳⼦?8.如图所⽰这是⼀个长6分⽶、宽4分⽶、⾼2分⽶的⽊箱,⽤三根铁丝捆起来,打结处⽤1分⽶铁丝.这三根铁丝总长⾄少是多少⽶?(8)9.⽤棱长1厘⽶的⼩正⽅体摆成稍⼤⼀些的正⽅体,⾄少需要多少个⼩正⽅体?10.⽤棱长1厘⽶的⼩正⽅体摆成棱长是3厘⽶的⼤正⽅体,需要多少个⼩正⽅体?7.⽤棱长1厘⽶的⼩正⽅体摆成⼀个⼤正⽅体,需要()个⼩正⽅体.A.4B.16C.50D.6412.⽤边长1厘⽶的⼩正⽅形摆成⼀个⼤正⽅形,需要()⼩正⽅形A.8B.27C.49D.7213.把⼀个长6厘⽶、宽4厘⽶、⾼5厘⽶的长⽅体⽊块表⾯全部涂成红⾊,然后切成棱长1厘⽶的⼩正⽅体⽊块.(1)切开后有多少个⼩正⽅体⽊块分别有三个⾯、两个⾯、⼀个⾯被涂成红⾊?(2)切开后有多少个⼩正⽅体⽊块没有染上红⾊(切⾯都是⽩⾊)?14.把⼀个长6厘⽶、宽3厘⽶、⾼5厘⽶的长⽅体⽊块表⾯全部涂成红⾊,然后切成棱长1厘⽶的⼩正⽅体⽊块.问:(1)切开后有多少个⼩正⽅体⽊块分别有三个⾯、两个⾯、⼀个⾯被涂成红⾊?(2)切开后有多少个⼩正⽅体⽊块没有染上⾊?15.⼀个表⾯涂满红⾊的⼩正⽅体,在它的每个⾯都等距离地切两⼑.三个⾯、两个⾯、⼀个⾯上涂红⾊的⼩正⽅体各有⼏个?16.把⼀个长6厘⽶、宽4厘⽶、⾼3厘⽶的长⽅体⽊块表⾯全部涂成红⾊,然后切成棱长1厘⽶的⼩正⽅体⽊块,这些⼩正⽅体恰好有两个⾯涂上红⾊的有多少个?17.⼀个长⽅体的长、宽、⾼分别是9厘⽶、8厘⽶、7厘⽶,把长、宽、⾼都扩⼤⾄原来的2倍,它的表⾯积扩⼤为原来的多少倍?18. ⼀个长⽅体的长、宽、⾼分别是10厘⽶、8厘⽶、6厘⽶,把长、宽、⾼都扩⼤⾄原来的3倍,它的表⾯积扩⼤为原来的多少倍?19. ⼀个长⽅体棱长总和是172厘⽶,已知长是宽的1.2倍,宽是⾼的1.5倍,求这个长⽅体的表⾯积.20.⼀个正⽅体的棱长总和84厘⽶,它的体积和表⾯积分别是多少?21.如图所⽰,这个⽴体图形由20个棱长为1厘⽶的⼩正⽅体⽊块堆积⽽成,求它的表⾯积.(21)(22)(23)22. 如图所⽰,这个⽴体图形由13个棱长为1厘⽶的⼩正⽅体⽊块堆积⽽成,求它的表⾯积.23.如图是⼀个⽤棱长1厘⽶的⼩正⽅体摆成的物体.(1)这个物体的表⾯积是多少?(2)要把这个物体补成⼀个⼤正⽅体,这个⼤正⽅体的表⾯积⾄少是多少?。



五年级奥数讲义第13讲--长方体和正方体(一)work Information Technology Company.2020YEAR第13讲长方体和正方体(一)一、知识要点在数学竞赛中,有许多有关长方体、正方体的问题。
解答稍复杂的立体图形问题要注意几点:1.必须以基本概念和方法为基础,同时把构成几何图形的诸多条件沟通起来;2.依赖已经积累的空间观念,观察经过割、补后物体的表面积或体积所发生的变化;3.求一些不规则的物体体积时,可以通过变形的方法来解决。
二、精讲精练【例题1】一个零件形状大小如下图:算一算,它的体积是多少立方厘米表面积是多少平方厘米(单位:厘米)【思路导航】(1)可以把零件沿虚线分成两部分来求它的体积,左边的长方体体积是10×4×2=80(立方厘米),右边的长方体的体积是10×(6-2)×2=80(立方厘米),整个零件的体积是80×2=160(立方厘米);(2)求这个零件的表面积,看起来比较复杂,其实,朝上的两个面的面积和正好与朝下的一个面的面积相等;朝右的两个面的面积和正好与朝左的一个面的面积相等。
因此,此零件的表面积就是(10×6+10×4+2×2)×2=232(平方厘米)。
想一想:你还能用别的方法来计算它的体积吗?练习1:1.一个长5厘米,宽1厘米,高3厘米的长方体,被切去一块后(如图),剩下部分的表面积和体积各是多少?2.把一根长2米的长方体木料锯成1米长的两段,表面积增加了2平方分米,求这根木料原来的体积。
3.有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如图),求切掉正方体后的表面积和体积各是多少?【例题2】有一个长方体形状的零件,中间挖去一个正方体的孔(如图),你能算出它的体积和表面积吗(单位:厘米)【思路导航】(1)先求出长方体的体积,8×5×6=240(立方厘米),由于挖去了一个孔,所以体积减少了2×2×2=8(立方厘米),这个零件的体积是240-8=232(立方厘米);(2)长方体完整的表面积是(8×5+8×6+6×5)×2=236(平方厘米),但由于挖去了一个孔,它的表面积减少了一个(2×2)平方厘米的面,同时又增加了凹进去的5个(2×2)平方厘米的面,因此,这个零件的表面积是236+2×2×4=252(平方厘米)。
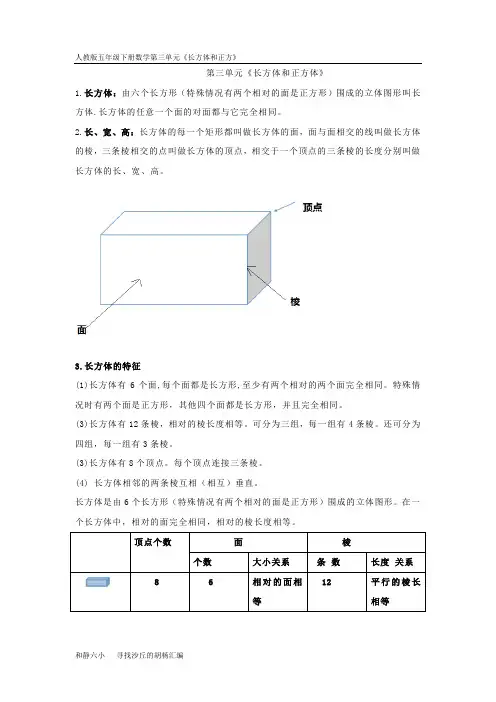
第三单元《长方体和正方体》1.长方体:由六个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫长方体.长方体的任意一个面的对面都与它完全相同。
2.长、宽、高:长方体的每一个矩形都叫做长方体的面,面与面相交的线叫做长方体的棱,三条棱相交的点叫做长方体的顶点,相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3.长方体的特征(1)长方体有6个面,每个面都是长方形,至少有两个相对的两个面完全相同。
特殊情况时有两个面是正方形,其他四个面都是长方形,并且完全相同。
(3)长方体有12条棱,相对的棱长度相等。
可分为三组,每一组有4条棱。
还可分为四组,每一组有3条棱。
(3)长方体有8个顶点。
每个顶点连接三条棱。
(4) 长方体相邻的两条棱互相(相互)垂直。
长方体是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
在一个长方体中,相对的面完全相同,相对的棱长度相等。
顶点个数面棱个数大小关系条数长度关系8 6 相对的面相等12 平行的棱长相等4.棱长总和公式:长方体棱长总和=4条长+4条宽+4条高=(长+高+宽)×4宽=棱长之和÷4-长-高长=棱长之和÷4-宽-高高=棱长之和÷4-宽-长二、正方体的认识:1. 正方体的认识:正方体是由6个完全相同的正方形围成的立体图形。
正方体有6个面,12条棱,8个顶点,每个面都是正方形,面积都相等。
每条棱的长度都相等。
正方体的长、宽、高都相等,统称棱长。
2.长方体和正方体的关系:正方体是一种特殊的长方体。
3.正方体棱长之和:棱长×12=棱长之和棱长之和÷12=棱长4.长方体的表面积(1)长方体和正方体6个面的总面积,叫做它的表面积。
(2)表面积计算公式①.因为长方体有“上”、“下”、“前”、“后”、“左”、“右”6个面,相对的2个面相等,所以先算上下两个面,再算前后两个面,最后算左右两个面。
②长方体的表面积=(长×宽+长×高+宽×高)×2用字母表示: S=(ab+ah+bh)×2长方体表面积=(长×宽+长×高+宽×高)×2设一个长方体的长、宽、高分别为a、b、c,则它的表面积S:S = 2ab + 2bc+ 2ca= 2 ( ab + bc + ca)长方体没盖的表面积=长×宽+长×高×2 +宽×高×2③特殊长方体的表面积(有两个面是正方形)正方形的两个面完全相同,其余四个面完全相同。


第三单元《长方体和正方体》1.长方体:由六个长方形(特殊情况有两个相对的面是正方形)围成的立体图形叫长方体.长方体的任意一个面的对面都与它完全相同。
2.长、宽、高:长方体的每一个矩形都叫做长方体的面,面与面相交的线叫做长方体的棱,三条棱相交的点叫做长方体的顶点,相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。
3.长方体的特征(1)长方体有6个面,每个面都是长方形,至少有两个相对的两个面完全相同。
特殊情况时有两个面是正方形,其他四个面都是长方形,并且完全相同。
(3)长方体有12条棱,相对的棱长度相等。
可分为三组,每一组有4条棱。
还可分为四组,每一组有3条棱。
(3)长方体有8个顶点。
每个顶点连接三条棱。
(4) 长方体相邻的两条棱互相(相互)垂直。
长方体是由6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形。
在一个长方体中,相对的面完全相同,相对的棱长度相等。
顶点个数面棱个数大小关系条数长度关系8 6 相对的面相等12 平行的棱长相等4.棱长总和公式:长方体棱长总和=4条长+4条宽+4条高=(长+高+宽)×4宽=棱长之和÷4-长-高长=棱长之和÷4-宽-高高=棱长之和÷4-宽-长二、正方体的认识:1. 正方体的认识:正方体是由6个完全相同的正方形围成的立体图形。
正方体有6个面,12条棱,8个顶点,每个面都是正方形,面积都相等。
每条棱的长度都相等。
正方体的长、宽、高都相等,统称棱长。
2.长方体和正方体的关系:正方体是一种特殊的长方体。
3.正方体棱长之和:棱长×12=棱长之和棱长之和÷12=棱长4.长方体的表面积(1)长方体和正方体6个面的总面积,叫做它的表面积。
(2)表面积计算公式①.因为长方体有“上”、“下”、“前”、“后”、“左”、“右”6个面,相对的2个面相等,所以先算上下两个面,再算前后两个面,最后算左右两个面。
②长方体的表面积=(长×宽+长×高+宽×高)×2用字母表示: S=(ab+ah+bh)×2长方体表面积=(长×宽+长×高+宽×高)×2设一个长方体的长、宽、高分别为a、b、c,则它的表面积S:S = 2ab + 2bc+ 2ca= 2 ( ab + bc + ca)长方体没盖的表面积=长×宽+长×高×2 +宽×高×2③特殊长方体的表面积(有两个面是正方形)正方形的两个面完全相同,其余四个面完全相同。
五年级年级下册数学:《正方体与长方体》知识点+练习时间:___________ 学生:________ 授课老师:_______课堂安排:新课一、长方体特点:(1)有6个面,8个顶点,12条棱,相对的面的面积相等,相对的棱的长度相等。
(2)一个长方体最多有6个面是长方形,最少有4个面是长方形,最多有2个面是正方形。
二、正方体特点:(1)正方体有12条棱,它们的长度都相等。
(2)正方体有6个面,每个面都是正方形,每个面的面积都相等。
(3)正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体。
相同点不同点面棱长方体都有6个面,12条棱,8个顶点。
6个面都是长方形。
(有可能有两个相对的面是正方形)。
相对的棱的长度都相等正方6个面都是正方形。
12条棱都相等。
体针对练习一【对应练习1】长、宽、高都相等的长方体叫________,它是特殊的________。
【对应练习2】用棱长为2cm的小正方体拼成一个大正方体,至少需要( )个这样的小正方体。
【对应练习3】正方体有()个面,每个面都(),都是()形,有()条棱,12条棱长度(),叫做正方体的棱长,有()个顶点,正方体是特殊的()。
【对应练习4】正方体是特殊的( ),是长、宽、高都( )的长方体。
三、长方体、正方体有关棱长计算公式:长方体的棱长总和=(长+宽+高)×4=长×4+宽×4+高×4L=(a+b+h)×4长=棱长总和÷4-宽-高a=L÷4-b-h宽=棱长总和÷4-长-高b=L÷4-a-h高=棱长总和÷4-长-宽h=L÷4-a-b正方体的棱长总和=棱长×12L=a×12正方体的棱长=棱长总和÷12a=L÷12针对练习二【典型题1】一个长方体的棱长总和是24厘米,从一个顶点出发的三条棱的和是( )厘米。
第13讲长方体和正方体(一)一、知识要点在数学竞赛中,有许多有关长方体、正方体的问题。
解答稍复杂的立体图形问题要注意几点:1.必须以基本概念和方法为基础,同时把构成几何图形的诸多条件沟通起来;2.依赖已经积累的空间观念,观察经过割、补后物体的表面积或体积所发生的变化;3.求一些不规则的物体体积时,可以通过变形的方法来解决。
二、精讲精练【例题1】一个零件形状大小如下图:算一算,它的体积是多少立方厘米?表面积是多少平方厘米?(单位:厘米)练习1:1.一个长5厘米,宽1厘米,高3厘米的长方体,被切去一块后(如下左图),剩下部分的表面积和体积各是多少?2.有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如上右图),求切掉正方体后的表面积和体积各是多少?【例题2】有一个长方体形状的零件,中间挖去一个正方体的孔(如图),你能算出它的体积和表面积吗?(单位:厘米)练习2:1.有一个形状如下图的零件,求它的体积和表面积。
(单位:厘米)。
第1题第2题第3题2.有一个棱长是4厘米的正方体,从它的一个顶点处挖去一个棱长是1厘米的正方体后,剩下物体的体积和表面积各是多少?3.如果把上题中挖下的小正方体粘在另一个面上(如图),那么得到的物体的体积和表面积各是多少?【例题3】一个正方体和一个长方体拼成了一个新的长方体,拼成的长方体的表面积比原来的长方体的表面积增加了50平方厘米。
原正方体的表面积是多少平方厘米?1.把两个完全一样的长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个长方体的表面积的和减少了46平方厘米,而长是原来长方体的2倍。
如果拼成的长方体的长是24厘米,那么它的体积是多少立方厘米?2.一根长80厘米,宽和高都是12厘米的长方体钢材,从钢材的一端锯下一个最大的正方体后,它的表面积减少了多少平方厘米?【例题4】把11块相同的长方体砖拼成一个大长方体。
已知每块砖的体积是288立方厘米,求大长方体的表面积。
长方体和正方体
1.一个长方体棱长总和是60厘米,已知长是宽
的1.5倍,宽是高的2倍,求这个长方体的长、宽、高.
2.一个长方体棱长总和是96厘米,已知长是宽
的1.5倍,宽是高的2倍,求这个长方体的长、宽、高.
3.一个长方体棱长总和是103.2厘米,已知长
是宽的1.2倍,宽是高的1.5倍,求这个长方体的长、宽、高.
4.一个正方体的棱长总和是93.6厘米,它的棱
长是多少?
5.一个长25厘米、宽20厘米、高18厘米的长
方体盒子,如果按如图所示的虚线用绳子捆起来,不计接头处绳子的长度,需要多长的绳子?
(5)(6)(7)
6.一个长2.2米、宽1.8米、高2米的长方体
木箱,按如图所示的虚线用绳子捆起来,不
计接头处绳子的长度,需要多长的绳子?
7.一个棱长6分米的正方体物品,按如图所示
的虚线用绳子捆起来,接头处是40厘米,那么
至少需要多长的绳子?
8.如图所示这是一个长6分米、宽4分米、高2
分米的木箱,用三根铁丝捆起来,打结处用1分
米铁丝.
这三根铁丝总长至少是多少米?
(8)
9.用棱长1厘米的小正方体摆成稍大一些的正方
体,至少需要多少个小正方体?
10.用棱长1厘米的小正方体摆成棱长是3厘米
的大正方体,需要多少个小正方体?
7.用棱长1厘米的小正方体摆成一个大正方体,
需要()个小正方体.
A.4
B.16
C.50
D.64
12.用边长1厘米的小正方形摆成一个大正方形,
需要()小正方形
A.8
B.27
C.49
D.72
13.把一个长6厘米、宽4厘米、高5厘米的长方体木块表面全部涂成红色,然后切成棱长1厘米的小正方体木块.
(1)切开后有多少个小正方体木块分别有三个面、两个面、一个面被涂成红色?
(2)切开后有多少个小正方体木块没有染上红色(切面都是白色)?
14.把一个长6厘米、宽3厘米、高5厘米的长方体木块表面全部涂成红色,然后切成棱长1厘米的小正方体木块.问:
(1)切开后有多少个小正方体木块分别有三个面、两个面、一个面被涂成红色?
(2)切开后有多少个小正方体木块没有染上色?
15.一个表面涂满红色的小正方体,在它的每个面都等距离地切两刀.三个面、两个面、一个面上涂红色的小正方体各有几个?
16.把一个长6厘米、宽4厘米、高3厘米的长方体木块表面全部涂成红色,然后切成棱长1厘米的小正方体木块,这些小正方体恰好有两个面涂上红色的有多少个?
17.一个长方体的长、宽、高分别是9厘米、8厘米、7厘米,把长、宽、高都扩大至原来的2倍,它的表面积扩大为原来的多少倍?
18. 一个长方体的长、宽、高分别是10厘米、8厘米、6厘米,把长、宽、高都扩大至原来的3倍,它的表面积扩大为原来的多少倍?
19. 一个长方体棱长总和是172厘米,已知长是宽的1.2倍,宽是高的1.5倍,求这个长方体的表面积.
20.一个正方体的棱长总和84厘米,它的体积和表面积分别是多少?
21.如图所示,这个立体图形由20个棱长为1厘米的小正方体木块堆积而成,求它的表面积
.
(21)(22)(23)
22. 如图所示,这个立体图形由13个棱长为1厘米的小正方体木块堆积而成,求它的表面积.
23.如图是一个用棱长1厘米的小正方体摆成的物体.(1)这个物体的表面积是多少?
(2)要把这个物体补成一个大正方体,这个大正方体的表面积至少是多少?
24.棱长为1厘米的正方体,如图所示叠放,当叠放到5层时,这个立体图形的表面积是多少?
(24)
25.把一个长方体切成两个完全一样的正方体,表面积增加了32平方厘米.原来长方体的表面积是多少平方厘米?
26. 把一个长方体切成三个一样的正方体,表面积增加了40平方厘米.原来长方体的表面积是多少平方厘米?
27.一个正方体棱长8厘米,把它切成两个完全一样的长方体.每个长方体的表面积是多少?28.一个正方体木块的表面积是192平方厘米,把它锯成体积相等的8个正方体小木块.每个小木块的表面积是多少?
29.小东摆弄三块长7厘米、宽6厘米、高4厘米的长方体积木,他要把它们拼成一个表面积最小的长方体.这个大长方体的表面积是多少?
30. 军军摆弄三块长6厘米、宽4厘米、高3厘米的长方体积木,他要把它们拼成一个表面积最小的长方体.这个大长方体的表面积是多少?
31.玲玲准备把四盒英语磁带用彩色纸包装起来,一个磁带的长是11厘米,宽7厘米,厚度15毫米.那么,包装这四盒磁带至少需要多少平方厘米的彩纸(重叠的部分大约需要彩纸80平方厘米)?
32.三个正方体的棱长分别是2厘米、2厘米、5厘米,将它们粘合在一起,可得到一个新的几何体.问:
(1)怎样粘才能使得到的新几何体的表面积最小?(画图表示)
(2)这个最小表面积是多少平方厘米?
33.如图1、如图2所示,从两个相同的长方体上分别挖去一个棱长是1厘米的小正方体,求这两
个立体图形的表面积(单位:厘米)
.
(33) (34)
34.如图,从两个相同的长方体上分别挖去一个棱长是1厘米的小正方体,求这两个立体图形的表面积(单位:厘米).
35.如图,在一个长6厘米、宽5厘米、高4厘米的长方体木块中挖去一个棱长2厘米的小正方体的孔,这个长方体现在的表面积是多少?
(35) (36) (37)
36.如图,在一个长5厘米、宽4厘米、高3厘米的长方体上搭上一个棱长是2厘米的小正方体木块,搭成的物体表面积是多少?
37.棱长1分米的正方体,沿AB 棱垂直切4刀,沿BF 棱垂直切5刀,沿BD 水平切6刀,共得到大小不一的210个小长方体.这210个小长方体表面积的和是多少?
38.一个正方体木块,棱长6分米,沿水平方向将它锯成4份,每份又锯成5条,每条又锯成3小块,共得到大大小小的60个小长方体.这60个小长方体的表面积总和是多少?
39.某长方体的长、宽、高分别是10厘米、8厘米、4厘米,现在沿长边垂直切5刀,沿宽边垂直切3刀,沿高边水平切2刀,求所得小长方体表面积的总和.
40.如图所示,立体图形是14个棱长为5厘米的立方体组成的,求这个立体图形的表面积
.
(40)。