全加器电路设计

全加器与半加器原理及电路设计全加器是一种电子逻辑电路，用于执行二进制加法。

它由三个输入端(A, B, Cin)和两个输出端(S, Cout)组成。

其中，输入端A和B是要相加的二进制位，Cin是前一位的进位，输出端S是和的结果，Cout是是否有进位。

全加器可以通过组合多个半加器来构建。

半加器是全加器的组成部分，它只有两个输入端(A, B)和两个输出端(S, Cout)。

半加器只能够完成一位二进制加法，不考虑进位情况。

其中，输入端A和B是要相加的二进制位，输出端S是和的结果，Cout是是否有进位。

半加器的电路设计相对简单，可以通过逻辑门实现。

接下来，我将详细介绍全加器和半加器的原理和电路设计。

1.半加器原理及电路设计：半加器的真值表如下：A ，B ， S ， Cout0，0，0，00，1，1，01，0，1，01，1，0，1可以看出，输出端S等于两个输入端A和B的异或结果，输出端Cout等于两个输入端A和B的与运算结果。

半加器的电路设计可以使用两个逻辑门实现。

一个逻辑门用于计算和的结果S，另一个逻辑门用于计算进位Cout。

S = A xor BCout = A and B逻辑门可以采用与门、或门和异或门实现。

常用的逻辑门包括与非门(NAND)和异或门(XOR)。

所以，半加器的电路设计可以使用两个与非门和一个异或门实现。

2.全加器原理及电路设计：全加器的真值表如下：A ，B ， Cin ， S ， Cout0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1可以看出，输出端S等于三个输入端A、B和Cin的异或结果，输出端Cout等于输入端A、B和Cin的与运算结果和A和B的或运算结果的与运算结果。

全加器可以由两个半加器和一个或门组成。

其中，两个半加器用于计算S的低位和Cout的低位，而或门用于计算Cout的高位。

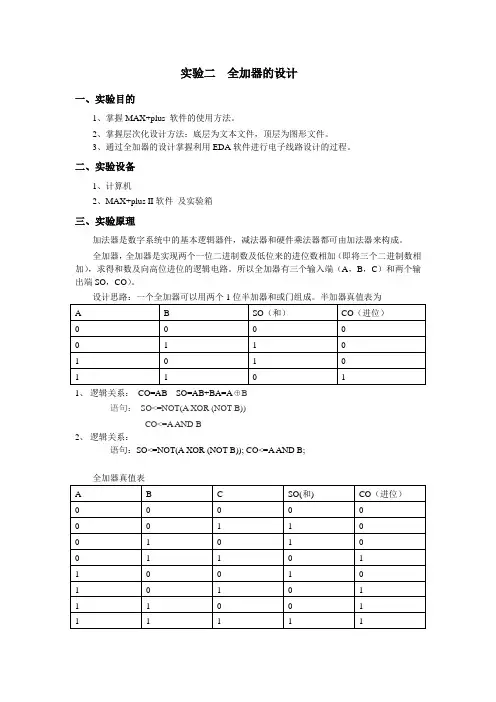
实验二全加器的设计一、实验目的1、掌握MAX+plus 软件的使用方法。

2、掌握层次化设计方法：底层为文本文件，顶层为图形文件。

3、通过全加器的设计掌握利用EDA软件进行电子线路设计的过程。

二、实验设备1、计算机2、MAX+plus II软件及实验箱三、实验原理加法器是数字系统中的基本逻辑器件，减法器和硬件乘法器都可由加法器来构成。

全加器，全加器是实现两个一位二进制数及低位来的进位数相加（即将三个二进制数相加），求得和数及向高位进位的逻辑电路。

所以全加器有三个输入端（A，B，C）和两个输出端SO，CO）。

1、逻辑关系：CO=AB SO=AB+BA=A⊕B语句：SO<=NOT(A XOR (NOT B))CO<=A AND B2、逻辑关系：语句：SO<=NOT(A XOR (NOT B)); CO<=A AND B;SO=A⊕B⊕C CO=AB+CA+CB四、实验内容1、半加器的设计：完成源程序的编辑、编译、仿真。

2、两输入或门的设计：完成源程序的编辑、编译、仿真。

3、全加器的设计：完成源程序的编辑、编译、仿真。

五、实验步骤1、启动MAX+plus II 10.0 软件2、底层文件：新建文件文本文件：（1）File \ New \Text Editor File（2）在文本文件上输入代码（3）保存文本文件：File\Save\H-adder.vhd 扩展名为*.vhd（4）设置为当前文件：点击File\Project\set project to current file 设置项目为当前文件（5）编译1）选择芯片型号：点击Assign\Device：Ep1k30QC208-32）编译:点击MAX+plus II \ Compiler \ Start 开始编译,生成.pof 文件(CPLD) （6）仿真1）启动ＭaxplusII\Ｗavefrom editor 菜单，进入波形编辑窗口；2）导入输入输出节点：将鼠标移至空白处并单击鼠标右键，Enter Nodes from SNF 将欲仿真的所有Ｉ／Ｏ管脚加入。

一位全加器的设计全加器的主要作用是将两个二进制数相加，并产生一个结果和一个进位。

在设计全加器时，我们需要考虑以下几个方面：输入信号的处理、逻辑门的选择、进位的传递、和输出结果的计算。

首先，我们需要考虑输入信号的处理。

一个全加器需要接收两个二进制数和一个进位作为输入信号。

每个输入信号都可以用一个二进制位表示，这些位可以通过电路的输入端口进入电路。

在设计全加器时，我们需要确定如何使用这些输入信号。

其次，我们需要选择逻辑门来实现全加器。

逻辑门是数字电路的基本组件，通常用于实现计算和逻辑运算。

在设计全加器时，我们可以使用与门、或门和异或门来完成计算。

接下来，我们需要实现进位的传递。

当两个二进制数相加时，如果它们的和超过了二进制数能够表示的范围，就会产生一个进位。

为了实现进位的传递，我们可以使用逻辑门来判断是否产生了进位，并将进位传递到高位。

最后，我们需要计算输出结果。

一个全加器的输出结果是一个和位和一个进位位。

和位表示两个输入位的和，进位位表示是否产生了进位。

我们可以通过使用逻辑门和输入信号来计算输出结果。

下面是一个典型的全加器电路的设计：首先，我们将输入信号连接到三个输入端口。

一个输入端口用于接收两个输入二进制数，另一个输入端口用于接收进位。

接下来，我们将输入信号与逻辑门连接起来。

我们可以使用两个异或门来实现和位的计算，然后使用一个与门计算进位。

最后，我们将输出信号连接到两个输出端口。

一个输出端口用于输出和位，另一个用于输出进位位。

在实际设计中，我们需要综合考虑多个全加器的连接，以实现更复杂的计算。

这可以通过将多个全加器链接成一个加法器来实现。

加法器是一个包含多个全加器的数字电路，可以将更长的二进制数相加。

总结起来，全加器是一个重要的数字电路组件，用于将两个二进制数相加。

在全加器的设计过程中，我们需要考虑输入信号的处理、逻辑门的选择、进位的传递、和输出结果的计算。

通过合理选择逻辑门和连接输入输出信号，我们可以实现一个高效的全加器。

一位二进制全加器电路设计设计一个二进制全加器电路，听上去是不是有点高深？别担心，让我们轻松聊聊这个话题！全加器，顾名思义，就是用来加数字的。

我们知道，二进制就是零和一，简单又直接。

想象一下，如果你有两个数字，比如说 0 和 1，想把它们加在一起，全加器就像是你身边的小助手，轻松搞定。

你可能会问，全加器到底怎么工作的呢？其实很简单，它有三个输入，两个是要加的数字，另一个是进位。

然后，它会输出一个和以及可能的进位。

就像你在朋友家聚会，大家一起分享食物，有时候多出来的盘子得另找地方放。

怎么设计一个全加器电路呢？首先得搞清楚真值表，这是一个神奇的表格，它把所有可能的输入和对应的输出都列出来。

就像是你的购物清单，列出你要买的每一样东西。

比如说，如果两个输入都是 0，进位也是 0，输出当然是 0。

再比如，输入是 1 和 0，进位为 0，那输出就会是 1。

再往下看，如果两个输入都是 1，那就得看看进位了。

这就像是在厨房忙碌，偶尔得看看烤箱里的蛋糕，确保它不会烤焦。

设计电路的时候，你得选用逻辑门。

常见的有与门、或门和非门。

想象一下，逻辑门就像是开关，你可以通过这些开关来控制电流的流动。

与门就像是要求所有的朋友都到齐才能开始聚会，而或门则是只要一个人到就行，非门就是调皮的那位朋友，总是反着来。

通过组合这些逻辑门，就能实现我们的全加器。

接下来是连接这些门，得小心翼翼，不然就像你在拼积木，拼错了就没法再玩了。

我们把两个输入连接到与门和或门，进位也得适当地连接上。

这样一来，所有的开关就齐齐整整，准备好接受输入，输出你期待的结果。

别忘了，布局得整齐，这样电路才能正常工作。

就像你的书桌，整洁才能专注。

还有一个小秘诀，利用Karnaugh图简化逻辑表达式。

这个图就像是拼图游戏，把复杂的逻辑关系变得简单明了，帮助我们找到最优的电路设计。

你看，设计电路并不复杂，只要一步一步来，就像学骑自行车，摔几次之后就能掌握平衡。

测试电路是非常重要的。

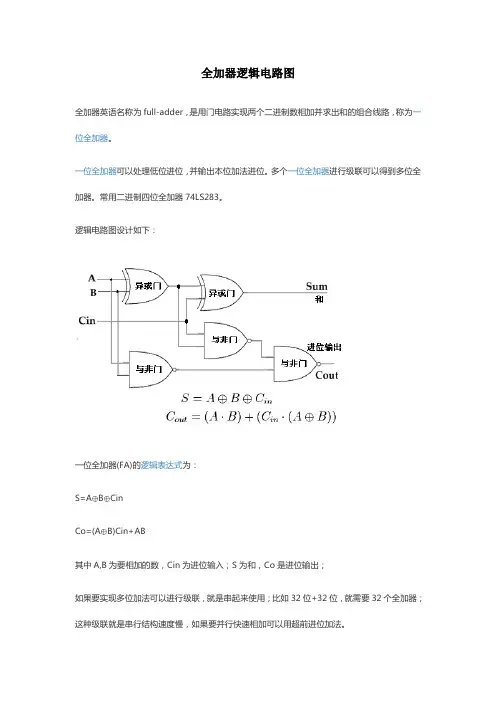
全加器逻辑电路图
全加器英语名称为full-adder，是用门电路实现两个二进制数相加并求出和的组合线路，称为一位全加器。

一位全加器可以处理低位进位，并输出本位加法进位。

多个一位全加器进行级联可以得到多位全加器。

常用二进制四位全加器74LS283。

逻辑电路图设计如下：
一位全加器(FA)的逻辑表达式为：
S=A⊕B⊕Cin
Co=(A⊕B)Cin+AB
其中A,B为要相加的数，Cin为进位输入；S为和，Co是进位输出；
如果要实现多位加法可以进行级联，就是串起来使用；比如32位+32位，就需要32个全加器；这种级联就是串行结构速度慢，如果要并行快速相加可以用超前进位加法。

扩展资料：
全加器是组合逻辑电路中最常见也最实用的一种，考虑低位进位的加法运算就是全加运算，实现全加运算的电路称为全加器。

而其功能设计可以根据组合逻辑电路的设计方法来完成。

通过逻辑门、74LS138译码器、74LS153D数据选择器来实现一位全加器的电路设计，并且实现扩展的两位全加器电路。

并且Multisim是一个专门用于电路设计与仿真的工具软件。

1位全加器电路设计全加器是一种组合逻辑电路，用于将两个二进制数相加，并输出和及进位。

一个1位全加器包含两个输入（被加数和加数）和两个输出（和和进位）。

全加器具有一个额外的输入（进位输入）来接收来自上一位的进位。

一个1位全加器可以使用与门（AND）、异或门（XOR）和或门（OR）来实现。

设计思路如下：1.将两个输入（被加数和加数）分别与一个异或门（XOR）连接，得到一个输出（和）。

2.将两个输入（被加数和加数）分别与一个与门（AND）连接，得到一个输出（进位）。

3.将两个输入的与门（AND）的输出（进位）与进位输入进行异或运算，得到最终的进位输出。

4.将输出（和）和最终进位输出作为全加器的输出。

下面是我对1位全加器的详细设计：首先，我们需要定义输入和输出信号：输入信号：A, B, Cin（被加数，加数，进位输入）输出信号：S, Cout（和，进位输出）接下来，我们可以按照设计思路，逐步实现1位全加器：Step 1: 设计异或门（XOR）的电路将输入A和B连接到一个异或门，得到一个信号X（X=AXORB）Step 2: 设计与门（AND）的电路将输入A和B连接到一个与门，得到一个信号Y（Y=AANDB）Step 3: 设计第一个异或门（XOR）的电路将信号X和进位输入Cin连接到一个异或门，得到一个信号Z（Z = X XOR Cin）Step 4: 设计与门（AND）的电路将信号X和进位输入Cin连接到一个与门，得到一个信号CarryOut （CarryOut = X AND Cin）Step 5: 设计或门（OR）的电路将信号Y和信号CarryOut连接到一个或门，得到输出信号Cout （Cout = Y OR CarryOut）Step 6: 设计或门（OR）的电路将信号X和信号Z连接到一个或门，得到输出信号S（S=XORZ）最后，我们将输入A、B和Cin以及输出S、Cout连接到1位全加器的电路中，即可实现1位全加器。

第4章全加器设计应用4.1全加器设计在计算机工程中，全加器是一种逻辑电路，用于将两个输入位和上一个进位位相加，并产生一个和位和一个进位位。

全加器是构成数字逻辑中任何计算机系统的基本构建模块之一一个全加器可以通过与门、或门和异或门组合构建。

它有三个输入（A、B和进位位C_in）和两个输出（和位S和进位位C_out）。

全加器的真值表如下所示：A B C_in S C_out0000000110010100110110010101011100111111全加器的电路图如下所示：_______________A_______，，____，，___AND1XOR1ORB_______，____，____，_________，_________，_____C_in ________，____4.2全加器的应用全加器是计算机系统中的关键组件，用于实现各种数学和逻辑运算。

下面是全加器的一些应用：1.加法器：全加器可以用来实现两个二进制数的加法运算。

将两个二进制数的每一位与对应的进位位输入到全加器中，从低位到高位依次相加，得到结果和位和进位位。

2.减法器：通过对减数取反，并在最低位的进位位上加上1，然后将减数和被减数与对应的进位位输入到全加器中，可以实现两个二进制数的减法运算。

3.乘法器：乘法器可以使用连续加法器来实现。

将两个二进制数的每一位与对应的进位位输入到全加器中，然后按照乘法运算规则依次相加，最终得到结果。

4.除法器：除法器可以使用连续减法器来实现。

将被除数和除数与对应的进位位输入到全加器中，然后按照除法运算规则依次相减，直到减数小于零为止，最终得到商和余数。

5.比较器：通过将两个二进制数的每一位与对应的进位位输入到全加器中，然后比较结果和进位位，可以判断两个二进制数的大小关系。

6.码转换器：全加器可以用来实现BCD码和8421码之间的转换。

BCD码是二进制编码和十进制数字之间的一种表示方法，而8421码是一种用来表示四位二进制数的编码。

组合逻辑电路设计之全加器半加器全加器和半加器是组合逻辑电路中常用的两种基本电路。

全加器和半加器可以用于实现二进制数的加法运算。

在本文中，将详细介绍全加器和半加器的设计原理和电路结构。

一、半加器半加器是一个用于实现两个一位二进制数相加求和的电路。

半加器的输入包括两个二进制数A和B，输出包括二进制求和信号S和进位信号C。

```A----，--?--SB----，，--CGND```半加器的输出S等于输入A和B的异或（XOR）结果，输出C等于输入A和B的与（AND）结果。

半加器的真值表如下所示：A，B，S，C---，---，---，---0，0，0，00，1，1，01，0，1，01，1，0，1二、全加器全加器是一个用于实现三个一位二进制数相加求和的电路。

全加器的输入包括两个二进制数A和B，以及一个进位信号Cin（来自上一位的进位或者是初始进位信号），输出包括二进制求和信号S和进位信号Cout （输出给下一位的进位信号）。

```A----，--?---SB ----，，--CoutCin --，--?-------CGND```全加器的输出S等于输入A、B和Cin的异或（XOR）结果，输出Cout等于输入A、B和Cin的任意两个的与（AND）结果和输入A、B和Cin的三个的或（OR）结果的与（AND）结果。

全加器的真值表如下所示：A ，B ， Cin ， S ， Cout---，---，-----，---，------0，0，0，0，00，0，1，1，00，1，0，1，00，1，1，0，11，0，0，1，01，0，1，0，11，1，0，0，11，1，1，1，1三、全加器的电路设计可以通过组合半加器的方式来设计一个全加器。

在全加器中，首先使用两个半加器实现输入A和B的求和结果（S1）和对应的进位（C1）；然后再使用一个半加器将输入A和B之间的进位信号（Cin）与求和结果（S1）相加，得到最终的求和结果（S）和进位信号（Cout）。

加法器电路设计全加器全加器是一种用于将两个二进制数字相加的电路，它包括两个输入和三个输出。

全加器可以用于将两个数字相加，并产生其和以及进位。

在设计全加器的过程中，我们需要考虑输入和输出的位数、进位和和的计算，并使用逻辑门来实现电路。

首先，我们需要确定输入和输出的位数。

假设我们设计的全加器有两个2位的输入A和B，以及一个进位输入C，输出结果和进位分别为S和C_out。

那么我们的设计目标就是将A、B和C相加，并将结果S和进位C_out输出。

接下来，我们需要考虑如何计算和以及进位。

和的计算可以通过异或门来实现，因为异或门输出只有当两个输入不同时为1时才为1、因此，我们可以使用两个异或门来计算和：S=(A⊕B)⊕C。

进位的计算可以通过与门来实现，因为与门只有当两个输入都为1时才为1、我们可以使用两个与门来计算进位：C_out = (A ∧ B) ∨ (C ∧ (A ⊕ B))。

这个表达式中，(A ∧ B)表示当A和B都为1时的进位，(C ∧ (A ⊕ B))表示A和B中只有一个为1且进位也为1时的进位，而∨操作符表示两个进位取或运算。

现在，我们已经确定了计算和和进位的逻辑表达式，下面我们来实现这个电路。

首先，我们需要使用逻辑门来实现异或和与运算。

异或门可以使用与门、或门和非门来实现。

我们可以使用如下的逻辑逻辑表达式来实现异或运算：A⊕B=(A∧¬B)∨(¬A∧B)。

与门可以使用与非门实现，即A∧B=¬(¬A∨¬B)。

或门可以直接使用或门实现。

我们可以使用这些逻辑门来实现全加器的电路。

首先，我们将输入A、B和C分别连接到两个异或门的输入端，将两个异或门的输出连接到一个异或门的输入端，得到和S。

接下来，我们将输入A和B分别连接到两个与非门的输入端，将两个与非门的输出连接到一个或门的输入端，得到进位C_out。

最后，我们需要将电路连接到其他的逻辑门或者其他的全加器，以构建更复杂的电路。

一． 设计原理。

1.全加器与脉冲信号发生器电路图U1、U2 和 U3A 组成一位全加器， 个加数”由 U1A 的 1、2 “2 脚输入， “进位”有 U8A 的 5 脚输入， “全加和”由 U2C 的 8 脚输出到 D 触发器 U4A 的数据输出端 D，进位输出到 U8A 的 数据输入端。

和 U3C 组成的基本 RS 触发器和单刀双掷无 U3B 锁按键 KP 一起组成脉冲发生器，每按一次 KP 在 U3C 的管脚 8 形成的一个正位脉冲给所有 D 触发器提供 CP 脉冲 2 累加器 A 电路图由双 D 触发器 U4 和 U5 组成的“移位寄存器 A”保存累加器 的一个加数 3.累加器 B 电路图由双 D 触发器 U6 和 U7 组成的“移位寄存器 B”保存累加器 的另一个加数，D 触发器 U8A 保存进位位 C4.累加器电路图按下 KR 键可使所有 D 触发器复位为全 0，复位后可通过KA3-KA0 键分别设置加数 A 的各个位，通过 KB3-KB0 键分别 设置另一个加数 B 的各个位， 通过 KC 设置来自低位的进位 C。

按 KP 键 4 次产生 4 各 CP 脉冲完成累加， 结果在寄存器 A 中， 向高位的进位在 C 中，寄存器 B 全为 0.二、制作调试过程 1、 步骤 （1） 打印： 3 个电路图分别打印在 3 张要求大小的硫酸 将 纸上 （2） 裁板：裁切 3 张比电路图大小大一点的铜板 （3） 压图： 用过热机将电路图压在铜板上， 冷却后撕去硫 酸纸，检查电路是否完整 （4） 腐蚀：将铜板放在三氯化铁腐蚀液中腐蚀 （5） 钻孔：用钻孔机钻孔 （6） 焊接：用电烙铁将每个元器件焊接在正确的位置上 2、 准备工作 用万能表检查有没有短路、断路情况。

三、 测试。

(1) 全加器与脉冲信号发生器的测试 A0,B0，C 接逻辑开关，VCC 接电源，GND 解地，S,CO，CP 分 别接发光二极管。

实验五全加器的设计及应用一、实验目的（1）进一步加深组和电路的设计方式。

（2）会用真值表设计半加器和全加器电路，验证其逻辑功能。

（3）把握用数据选择器和译码器设计全加器的方式。

二、预习要求（1）依照表5-1利用与非门设计半加器电路。

（2）依照表5-2利用异或门及与非门设计全加器电路。

三、实验器材（1）实验仪器：数字电路实验箱、万用表；（2）实验器件：74LS04、74LS0八、74LS20、74LS3二、74LS8六、74LS13八、74LS153；四、实验原理1.半加器及全加器电子数字运算机最大体的任务之一确实是进行算术运算，在机械中的四那么运算——加、减、乘、除都是分解成加法运算进行的，因此加法器便成了运算机中最大体的运算单元。

（1）半加器只考虑了两个加数本身，而没有考虑由低位来的进位（或把低位来的进位看成0），称为半加，完成半加功能的电路为半加器。

框图如图5-1所示。

一名半加器的真值表如表5-1所示。

表5-1半加器真值表1位半加器S C i A i Bi 和数向高位进位加数被加数图5-1 半加器框图由真值表写逻辑表达式：⎩⎨⎧=⊕=+=i i i ii i i i i i B A C B A B A B A S '' 画出逻辑图，如图5-2所示：（a ）逻辑图 （b ）逻辑符号 图5-2 半加器（2）全加器能进行加数、被加数和低位来的进位信号相加，称为全加，完成全加功能的电路为全加器。

依照求和结果给出该位的进位信号。

即一名全加器有3个输入端：i A （被加数）、i B （加数）、1-i C （低位向本位的进位）；2个输出端：i S （和数）、i C （向高位的进位）。

下面给出了用大体门电路实现全加器的设计进程。

1）列出真值表，如表5-2所示。

表5-2 全加器真值表从表5-2中看出，全加器中包括着半加器，当01=-i C 时，不考虑低位来的进位，确实是半加器。

而在全加器中1-i C 是个变量，其值可为0或1。

一位全加器简单设计原理
全加器是数字电路中常用的基本逻辑门之一，它能够实现三个二进制数字的加法运算，即两个数字和来自上一个加器的进位。

这篇文章介绍了一种简单的全加器设计原理，以及实现该设计所需的材料和步骤。

首先，我们需要以下材料：
1. 三个双极性晶体管
2. 两个电阻
3. 一个电源
接下来，我们需要按照以下步骤进行操作：
1. 将三个晶体管连接成一个三角形形状，其中两个晶体管的基极与集电极相连，另一个晶体管的发射极与另一个晶体管的集电极相连。

2. 将两个电阻连接在晶体管三角形的两个角上，以便提供电源和输入信号。

3. 将电源连接到电路中，确保正确极性和电压。

4. 输入两个二进制数字和一个进位信号到电路中，观察输出结果。

通过这种简单的设计原理，我们可以实现一个高效、低成本的全加器电路。

这种设计不仅适用于基本数字电路，还可以用于更复杂的计算机系统中，为数字处理提供更快速和准确的结果。

- 1 -。

加法器电路设计-全加器.doc全加器是一种数字电路，用于将两个位的二进制数字进行相加，并输出两位的和以及一位的进位。

它是一种更复杂的加法器，由多个逻辑门组成。

全加器常常用于计算机中的加法器电路，并且在计算机逻辑电路中起着非常重要的作用。

一般来说，一个全加器包括三个进位和三个输出端：两个输入端和一个输出端。

其中，两个输入端分别用来输入两个二进制数，而一个输出端则是用来输出两数相加的结果和进位数。

为了更好地理解全加器，我们需要先了解一下半加器。

半加器是一种将两个位的二进制数字进行相加，并输出两位的和的电路。

它也被称为是二进制加法器的最基础模块。

它包括两个输入端和两个输出端：一个是和，另一个是进位。

半加器的电路可以通过两个异或门和一个与门构成。

具体来说，半加器的实现方式如下：其中，XOR 表示异或门，AND 表示与门。

在半加器的电路中，A 和 B 分别表示两个输入端的数，S 表示输出端的和，C 表示进位。

因此，半加器的输出公式可以表示为：S = A ⊕ BC = A ∧ B根据半加器的电路原理，我们可以将两个半加器联用，从而构成一个全加器。

具体来说，全加器可以由两个半加器和一个 OR 门组成。

它的电路如下图所示：其中，A、B、Cin 分别表示两个输入端和进位端的二进制数，S、Cout 分别表示输出端的和和进位数。

由于我们需要同时考虑上一个进位和现在的两个输入数，因此进位信号需要同时输入到两个半加器中。

根据全加器的电路原理，我们可以得到它的输出公式：S = (A ⊕ B) ⊕ C inCout = (A ∧ B) ∨ (Cin ∧ (A ⊕ B))综上所述，全加器是基于半加器的基础上建立出来的，它可以处理更大量级的输入和输出。

在计算机中，全加器是十分重要的一个部分，因为它是实现二进制算术的基础。

通过逐级的组合，计算机可以实现加减乘除等操作，从而完成各种不同的计算任务。

设计全加器的实验报告设计全加器的实验报告一、引言在数字电路设计中，全加器是一种基本的组合逻辑电路，用于实现两个二进制数的相加运算。

全加器的设计对于计算机的运算速度和准确性至关重要。

本实验旨在通过设计和实现一个全加器电路，来深入了解全加器的原理和功能。

二、实验目的1. 了解全加器的工作原理和功能；2. 学习使用逻辑门和触发器设计和实现全加器电路；3. 掌握数字电路的布线和测试技巧。

三、实验器材和材料1. 逻辑门集成电路（如AND、OR、XOR等）；2. 触发器集成电路（如D触发器）；3. 连接线、电源等。

四、实验步骤1. 设计全加器的逻辑电路图；2. 根据逻辑电路图，选取合适的逻辑门和触发器进行电路实现；3. 进行电路布线，注意连接线的方向和接触的牢固性；4. 连接电源，检查电路是否正常工作；5. 使用示波器或逻辑分析仪对电路进行测试，验证全加器的功能和准确性。

五、实验结果与分析经过实验，我们成功设计并实现了一个全加器电路。

在输入两个二进制数和进位位的情况下，电路能够正确输出相应的和与进位结果。

通过观察示波器或逻辑分析仪上的波形图，我们可以清晰地看到电路的工作过程和信号传递路径。

六、实验总结通过本次实验，我们深入了解了全加器的原理和功能，并学会了使用逻辑门和触发器设计和实现全加器电路。

在实验过程中，我们也掌握了数字电路的布线和测试技巧。

通过实际操作和观察，我们对全加器的工作原理有了更深刻的理解。

然而，在实验中也遇到了一些问题。

例如，电路布线时容易出现连接错误或短路的情况，需要仔细检查和调试。

此外，选取适合的逻辑门和触发器也需要一定的经验和知识。

在今后的学习和实践中，我们将进一步加强对数字电路设计的理解和掌握，提高实验技能和解决问题的能力。

七、参考文献[参考书目1][参考书目2]以上为本次实验的报告内容，感谢老师和助教的指导和支持。

通过这次实验，我们不仅巩固了所学的理论知识，还提高了实践能力和解决问题的能力。