当前位置：文档之家 › 第10章__非参数检验

第10章__非参数检验

  • 格式：doc
  • 大小：97.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

医学统计学 -第10章 基于秩次的非参数检验

医学统计学 -第10章 基于秩次的非参数检验
Kruskal-Wallis H检验，用于推断计量资料或等级资料的 多个独立样本所来自的多个总体分布是否有差别。
H0：多个总体分布相同（或者中位数相等） H1：多个总体分布不同或不全相同（或者中位数不全相等）
26
例10.5
某医院用3种方法治疗15例胰腺癌患者，每种方 法各治疗5例，治疗后生存月数如下表，问3种方法的 疗效有无差别？
当n≤50时，通过查T界值表来确定是否波动过
大
T在界值范围内,波动不大
P>α
T在界值范围外或等于界值时，波动大，P≤α
11
(4) 查表及推断结论 查T界值表T0.05(16)=29~107 由于T＝28在上下界值范围外，所以P≤0.05。 按a=0.05检验水准拒绝H0，接受H1，可以 认为该厂工人尿铅含量不当地正常人有差异， 通过正负秩和的大小可以推断工人的尿铅含 量要高于正常人。
第十章 基于秩次的非参数检验
1
假设检验的方法分为两类
参数检验(parametric test)
已知总体分布类型，对未知参数（μ、π）进行统计推断 依赖于特定分布类型，比较的是参数 一般有严格的适用条件
如：样本来自正态分布、总体方差齐同等 这类方法比如：t检验、F检验等
非参数检验(nonparametric test)
Z
T n1(N 1) / 2 0.5
n1n2 (N 3 N
12N(N 1)
(t
3 j
t
j
))
2036 40(84 1) / 2 0.5
40 44 (843 84 (323 32) (323 32) (203 20)) 12 40 (84 1)
7.01
由于Z=7.01，大于Z0.05=1.96，所以P<0.05，按照α=0.05 检验水准拒绝H0，接受H1，可以认为夏冬两季居民体 内核黄素含量有差别。根据平均秩次可以知道夏季的含

统计学第十章 非参数统计方法

统计学第十章 非参数统计方法
– 非参数检验的假定条件要比参数检验宽松得多，不仅对 总体分布，而且对数据的测量层次。
4
参数统计与非参数统计
• 参数统计
– 对那些其总体分布族或称统计模型只依赖于有限个实参 数的问题，通称为“参数统计问题”，也就是说，总体 分布服从正态分布或总体分布已知条件下的统计检验， 称为参数检验，研究这一问题的统计分支称为参数统计。 参数统计的大部分方法要求所分析的数据至少是定距尺 度测量的结果。如统计学中的检验、检验等，都属于参 数检验。
13
符号检验
•符号检验的步骤
–建立假设
–计算检验统计量
•检验统计量S＋为S—和。 S＋表示为正符号的数目， S—表示 为负符号的数目。 S＋ + S— =n，n是符号的总数目。
–作出判定
•要对假设作出判定，需要找到一个值P。因为对于S＋和S—
来说，抽样分布是一个带有θ=0.5（表示成功的概率）的二
F0 (x) 表示一个特定的累积概率分布函数，也就是说，对于任一值，
x 值代表小于或等于值的那些预期结果所占的比例。于是，可以定
义
与 Sn (x) 之F0 (间x) 的差值，即
Sn (x) F，0 (x若) 对每一个x值来说，
两者与十分接近，也就是差异很小，则表明经验分布函数与特定
分布函数的拟合程度很高，有理由认为样本数据来自具有该理论
15
游程检验
• 游程检验的步骤
– 提出假设：零假设为：随机产生（随机性） – 检验统计量：R （游程个数）
– 随机性假设的拒绝域为 ：{R≤c1} ∪ {R ≥c2 },(c1< c2）
7
2. 单样本非参数检验
2020/2/4
8
χ2 检验

教育统计学第十章 非参数检验ppt课件

教育统计学第十章 非参数检验ppt课件

普通的秩和检验表，只给出n<=10情况下的实际临界值。当两个样本容量都较大时，T的抽
样分布接近于正态，可以近似地利用正态 T概率n分1 ( 布n 1 做2 秩n 2 和 1检) 验。T在抽样分布中的平均数为
规范误为
T
n1n 2 (n1 n 2 1) 12
Z T T T
例1：在一项关于模拟训练的实验中，以技工学校的学生为 对象，对5名学生用针对某一工种的模拟器进展训练，另外 让6名学生下车间直接在实习中训练，经过同样时间后对两 组人进展该工种的技术操作考核，结果如下：
例3：为了研讨RNA能否可以作为记忆促进剂，以老鼠为对 象分成实验组与控制组，实验组注射RNA，控制组注射生理 盐水，然后，在同样条件下学习走迷津，结果如下〔以所用 时间作为目的〕试检验两组有否显著差别。
实验组： 16.7,16.8,17.0,17.2,17.4,16.8,17.1,17.0,17.2,17.1,17 .2,17.5,17.2,16.8,16.3,16.9
期末课堂练习
第十章 非参数检验方法
一、两独立样本的差别显著性检验 1、秩和检验法 2、中数检验法 二、相关样本的差别显著性检验 1、符号检验法 2、符号秩次检验法 三、等级方差分析 1、克-瓦氏单向方差分析 2、弗里德曼双向等级方差分析
秩和检验
秩和法与参数检验中独立样本的t检验相对应。当“总体正态〞这一前提不成立，不能运用t检 验时以秩和法替代t检验。当两个样本都为顺序变量时，也需用秩和法来进展差别检验。
新法 90 84 87 85 90 94 85 88 92
例4的解
解: 配对 1 2 3 4 5 6 7 8 9
传统 85 88 87 86 82 82 70 72 80

常用的非参数检验（NonparametricTests）总结

常用的非参数检验（NonparametricTests）总结

常用的非参数检验（NonparametricTests）总结非参数检验(Nonparametric tests)是统计分析方法的重要组成部分，它与参数检验共同构成统计推断的基本内容。

参数检验是在总体分布形式已知的情况下，对总体分布的参数如均值、方差等进行推断的方法。

但是，在数据分析过程中，由于种种原因，人们往往无法对总体分布形态作简单假定，此时参数检验的方法就不再适用了。

非参数检验正是一类基于这种考虑，在总体方差未知或知道甚少的情况下，利用样本数据对总体分布形态等进行推断的方法。

由于非参数检验方法在推断过程中不涉及有关总体分布的参数，因而得名为“非参数”检验。

•两独立样本的非参数检验两独立样本的非参数检验是在对总体分布不甚了解的情况下，通过对两组独立样本的分析来推断样本来自的两个总体的分布等是否存在显著差异的方法。

独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。

SPSS中提供了多种两独立样本的非参数检验方法，其中包括曼-惠特尼U检验、K-S检验、W-W游程检验、极端反应检验等。

某工厂用甲乙两种不同的工艺生产同一种产品。

如果希望检验两种工艺下产品的使用是否存在显著差异，可从两种工艺生产出的产品中随机抽样，得到各自的使用寿命数据。

甲工艺：675 682 692 679 669 661 693乙工艺：662 649 672 663 650 651 646 652（1）曼-惠特尼U检验两独立样本的曼-惠特尼U检验可用于对两总体分布的比例判断。

其原假设：两组独立样本来自的两总体分布无显著差异。

曼-惠特尼U 检验通过对两组样本平均秩的研究来实现判断。

秩简单说就是变量值排序的名次，可以将数据按升序排列，每个变量值都会有一个在整个变量值序列中的位置或名次，这个位置或名次就是变量值的秩。

（2）K-S检验K-S检验不仅能够检验单个总体是否服从某一理论分布，还能够检验两总体分布是否存在显著差异。

两配对样本非参数检验

两配对样本非参数检验
相伴概率值为0.125，应该 认为训练前后学生成绩没有 变化
Wilcoxon检验结果如下两表所示。
出现了一个差值等于零的个案，删除此个 案，于是样本容量从10变成了9。符号为 正的有9个，秩和为45，符号为负的有0个， 秩和为0。这样，统计量W=0，构造的 Z=-2.673，近似相伴概率值p=Pr{｜Z｜ >=-2.673}=0.008，（Z服从标准正态分 布。）因而拒绝原假设，认为训练前后学 生的成绩有显著性差异。
训练后成绩
70.00 71.00 65.00 68.00 50.00 55.00 75.00 70.00 65.00 70.00
实验步骤
图10-23 在菜单中选择“2 Related Samples”命令
图10-24 “TwoRelatedSamples Tests” 对话框
设置配对 的样本
配对样本的几种检验方法，（其 中Marginal Homogeneity检 验是McNemar检验针对多取值 有序数据的推广方法）
01
按照符号检验的方法，将 第二组样本的各个观察值 减去第一组样本对应的观 察值，如果得到差值是一 个正数，则记为正号；差 值为负数，则记为负号。 （出现差值等于０时，删 除此个案，样本数ｎ相应 地减少。）
02
保留差值数据。根据差值 数据的绝对值大小按升序 排序，并求出相应的秩。
03
分别计算符号为正号的秩 和 W+、负号秩总合 W− 以及正号平均秩、 负号平均秩。
SPSS中有以下3种两配对样本非参数检验方法。
1．两配对样本的McNemar(麦克尼马尔)变化显著性检验
1 McNemar变化显著性检验以研究对象自身为对 照，检验其两组样本变化是否显著。 原假设：样本来自的两配对总体分布无显著差异。

【统计分析】非参数检验

【统计分析】非参数检验
α=0.05 2. 计算统计量： T+=62.5，T-=3.5
3. 查表与结论 查T界值表，T0.05（11）=10～56，T=3.5，在界 值范围外，P<0.05，拒绝H0。
符号检验（Sign test)
z n n 1 n
二、两样本比较的秩和检验 （Wilcoxon法）
适用条件：完全随机设计的两个样本比较，若不满足参数 检验的应用条件，则用本法；两个等级资料比较。
-0.45
-1
13
15.20
5.50
9.70
11
14
16.50
9.00
7.50
8.5
步骤
1. 建立假设：H0：差值的总体中位数=0， H1：差值的总体中位数0；
=0.05 2. 计算统计量
计算差值d，由小到大的顺序编秩次，并冠以原d 的正负号，然后分别求正负秩和，得到T+=73， T-=5，取秩和较小者作为检验统计量T=5 3. 查表及结论
1.0
2.5
4
17.00
6.50
10.50
12
5
13.00
5.50
7.50
8.5
6
18.00
13.50
4.50
5
7
17.50
10.00
7.50
8.5
8
10.20
10.20
0.00
-
9
10.00
10.00
0.00
-
10
10.50
9.50
1.00
2.5
11
13.80
6.80
7.00
6
12
3.03
3.48

第十章 非参数检验

第十章 非参数检验

10
11 12 13 14 15
70
85 75 68 70 65
66
67 65 70 78 67
76
80 90 86 85 75
SPSS过程演示
五、配对样本间非参数检验
1. 二项选择任务中配对样本间的差异比较 实例分析：某体育教师为了改进学校体育工作，有效增进 学生体质并提高其体育达标率，他采用匹配方法组织了两 个相等的教学试验组 ，一组作为控制组（group 1) ，继续
实例 2 ：教务处要求各院系在本科生毕业设计的成绩评定中，注意 成绩等级的人数分布，一般应符合如下表格中第一行所示的比例 。
某院65名本科生毕业设计成绩等级分布如下表第二行数字。请问该
院系学生毕业设计的成绩评定是否符合学校要求？
评定等级
要求比例 某院各等级人数
优秀
10% 8
良好
50% 43
中等
30% 13
使用传统教学方法；一个组作为实验组（group2），采用
新的教学方法。经过一年的教学周期后进行达标测试，结 果如下页表所示。
请问新的体育教学方法有无明显的优势？其是否可以
有效地提高学生的体育达标率？(McNemar检验)
体育教学训练方法改革试验测试结果（不同方法训练后学生达标情况登记） 序号 1 2 3 4 5 6 7 8 控制组 达标 不达标 不达标 达标 不达标 不达标 达标 不达标 实验组 达标 达标 不达标 达标 达标 达标 达标 不达标
星期日 星期一 10500 星期二 11800 星期三 12200 星期四 13200 星期五 14000 星期六 18500
顾客数 15000
解决方案
SPSS过程演示
（1）建立数据文件，包括两个变量：“时间”、“顾客数”； （2）打开“DATA”菜单条选中“Weight cases…”打开对话框，将“顾客数” 变

《医学统计学》第十章+非参数秩和检验

《医学统计学》第十章+非参数秩和检验

0.05
，即两个不同部位IL-6水平差值的总体中位数不为零
医学统计学（第7版）
符号秩和检验方法
（2）编秩次并求秩和统计量
首先求出各对数据的差值，见表的第（4）列；然后编秩次，按照差值绝
对值由小到大编秩，并按差值的正负给秩次加上正负号；若差值为“0”，舍
去不计，总的对子数也要减去此对子数（记为 n）；若差值的绝对值相等，取
➢ 查表法：查 T 界值表（附表8），
T0.05(23) 73 ~ 203
，
T T 91 73
T 在此范围内，P >0.05, 按 α=0.05水准无理由拒绝 H0 ，即实行良好
的口腔卫生6个月后，尚不能说明此项干预对牙周改善有显著效果。
，
医学统计学（第7版）
(3) 确定P 值，做出推断
检测结果如下表（书中表10-1所示） 。
白癜风病人的不同部位白介素指标（pg/ml）
病人号
(1)
白斑部位
(2)
正常部位
(3)
d=(3)-(2)
秩次
(5)
1
2
3
4
5
6
7
8
合计
40.03
97.13
80.32
25.32
19.61
14.50
49.63
44.56
88.57
88.00
123.72
39.03
24.37
上表中第（1）列按第（2）与（3）列数据统一编秩号，第（5）列为各等级的平均秩次，
第（6）列则是较小样本的秩和，本例中 T=T1=560.5, 将其代入公式得出：
zc

| T n1 ( N 1) / 2 | 0.5

医学统计学精品教学第十章-非参数检验精品文档

医学统计学精品教学第十章-非参数检验精品文档
2019/10/13
1
第十章 非参数秩和检验
吴库生 汕头大学医学院预防医学教研室
参数统计与非参数统计
1、参数统计（parametric statistics） 样本所来自的总体分布具有某个已知
的函数形式（如正态分布），而其中有 的参数是未知的，统计分析的目的是对 这些未知的参数进行估计或检验。
2019/10/13
28
符号秩和检验的SPSS实现
2019/10/13
秩和检验
29
Wilcoxon Signed Ranks Test
结 果
Ranks
N Mean RankSum of Ranks
光 电 比 色 法 -Negative Ranks
5a
氰 化 高 铁 法 Positive Ranks
5b
4.60 6.40
X
41.00±29.81
14.75±11.73
方差齐性检验:
F

S12(大) S22(小)
864.94816.2863 137.5929
F F0.05,(7,7) 4.99
P<0.05
两样本方差不齐，不能应用t检验
2019/10/13
医学统计学-秩和检验
31
采用Wilcoxon两独立样本秩和检验
10
Contents
第一节 配对资料的符号秩和检验（Wilcoxon配对法） 第二节 两独立样本比较的秩和检验（Wilcoxon两样本
法） 第三节 完全随机设计多个样本比较的秩和检验
（Kruskal-Ｗallis检验）
2019/10/13
秩和检验
11
第一节 两配对样本差值的符号秩和检验 (Wilcoxon signed rank test)

第10章非参数检验(精)

第10章非参数检验(精)

第10章非参数检验非参数检验是指在总体不服从正态分布或分布情况不明时，用来检验数据资料是否来自同一个总体假设的一类检验方法。

SPSS提供的非参数检验共有以下几种：Chi-Square：卡方检验（举例data16-01，data16-02）在前面介绍的方法中，往往都事先假定总体服从正态分布，然后对其均值或方差作检验。

但某个随机变量是否服从某种特定的分布是需要进行检验的。

可以根据以往的经验或实际的观测数据的分布情况，推测总体可能服从某种分布函数F(x)，利用这些样本数据来具体检验该总体分布函数是否真的就是F(x)。

卡方检验（Chi-Square）就是这样一种用来检验给定的概率值下数据来自同一总体的无效假设的方法。

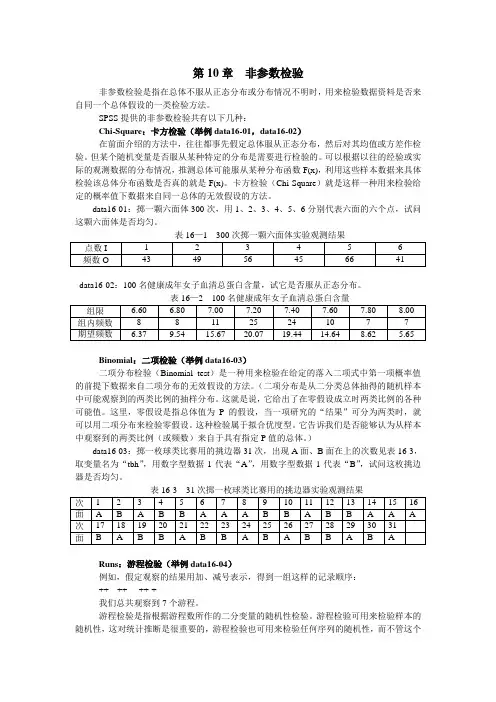
data16-01：掷一颗六面体300次，用1、2、3、4、5、6分别代表六面的六个点，试问这颗六面体是否均匀。

表16—1 300次掷一颗六面体实验观测结果data16-02：100名健康成年女子血清总蛋白含量，试它是否服从正态分布。

Binomial：二项检验（举例data16-03）二项分布检验（Binomial test）是一种用来检验在给定的落入二项式中第一项概率值的前提下数据来自二项分布的无效假设的方法。

（二项分布是从二分类总体抽得的随机样本中可能观察到的两类比例的抽样分布。

这就是说，它给出了在零假设成立时两类比例的各种可能值。

这里，零假设是指总体值为P的假设，当一项研究的“结果”可分为两类时，就可以用二项分布来检验零假设。

这种检验属于拟合优度型。

它告诉我们是否能够认为从样本中观察到的两类比例（或频数）来自于具有指定P值的总体。

）data16-03：掷一枚球类比赛用的挑边器31次，出现A面、B面在上的次数见表16-3，取变量名为“tbh”，用数字型数据1代表“A”，用数字型数据1代表“B”，试问这枚挑边器是否均匀。

表16-3 31次掷一枚球类比赛用的挑边器实验观测结果Runs：游程检验（举例data16-04）例如，假定观察的结果用加、减号表示，得到一组这样的记录顺序：++---++----++-+我们总共观察到7个游程。

第10章基于秩次的非参数检验教案

第10章基于秩次的非参数检验教案

2662.5
1384.5
显效
27
37
64
126－ 189
157.5
4252.5
5827.5
合计
69
120
189
7663
10292
H 0 ： 两 种 药 物 疗 效 的 总 体 分 布 相 同
H 1 ： 两 种 药 物 疗 效 的 总 体 分 布 相 同
0 .0 5
①先确定各等级的合计人数、秩范围和平 均秩，见表10-4的（4）栏、（5）栏和（6） 栏，再计算两样本各等级的秩和，见（7）栏 和（8）栏；
①省略所有差值为0的对子数，令余下的有效 对子数为n，见表10-1第（4）栏，本例 n=10；
➢若多个差值为0，可通过提高测量工具的精 度来解决。
②按差值的绝对值从小到大编秩，然后分别 冠以正负号。遇差值绝对值相等则取平均秩，称为 相同秩（ties）（样本较小时，如果相同秩较多， 检验结果会存在偏性，因此应提高测量精度，尽量 避免出现较多的相同秩）, 表10-1第（4）栏差值的 绝对值为2.29有2个，其秩依次应为1，2，皆取平 均秩为1.5，见表10-1第（5）.
式（10-4）计算校正的统计量值 Zc。
Zc
T n(n 1)/ 4 0.5
n(n 1)(2n 1)
(t
3 j
t
j
)
24
48
（10-4）
式中tj 为第j(j=1,2…)次相持所含相同秩次的个数。如例10-1，第1 次相持，
有两个差值的绝对值均为 2.29，则 t1=2；第 2 次相持，有两个差值均为 11.54，
由于秩统计量的分布与原数据总体分布
无关，具有较好的稳健性，可用于任何分 布类型的资料。

非参数检验(提纲)

非参数检验(提纲)

非参数检验参数检验方法，尤其是对计量资料，需要对研究的总体作一些比较严格的假定。

例如t检验法要求总体分布是正态分布等。

在实际工作中的许多资料不符合这种要求，因此以上的参数检验方法的使用受到了限制。

近代统计学家发明了对总体分布不必作限制性假定的检验技术，这种技术称为非参数检验（Nonparametric tests）。

非参数检验法是指在总体不服从正态分布或分布情况不明时，用来检验数据资料是否来自相同总体假设的一类检验方法。

由于它的假定前堤比参数检验方法少的多，而且在收集资料方面也十分简单，例如可以用“等级”或“符号”来评定观察的结果等，故这类方法在实际中有着广泛的应用。

第一节两相关样本的显著性检验1.1 符号检验法在配对实验中，将每对（或同一）实验单位（或先后）给予两种不同的处理，比较两种处理的效果有无差异或比较一组实验单位处理先后有无不同。

凡配对计量资料不服从正态分布要求时，可选用符号检验法（Sign test）。

例题1 有x,y 12对数据，它们的数值及相差符号由表1给出。

表1 本例的数据资料序号 1 2 3 4 5 6 7 8 9 10 11 12X 3 1 6 3 2 1 4 7 3 8 4 5Y 2 4 4 7 2 2 2 5 3 6 2 2 问这两个序列数值的差异是否具有显著性（α=0.05）？1.2 符号秩和检验法符号检验中只考虑配对数据x i-y i的符号，计算十分简便，但因没有考虑到x i-y i 差值的大小，因此对资料的利用不够充分，检验的灵敏度也不够好。

符号秩和检验法是上述方法的改进，由于关注到了差值的大小，故效果较好。

凡配对计量或计数的资料，可选用符号秩和检验法（Wilcoxon法）。

例题2 为研究长跑运动对增强普通高校学生的心功能效果，对某学院15名男生进行实验，经过5个月的长跑锻炼后观察其晨脉变化情况。

锻炼前后的晨脉数据如下。

问锻炼前后晨脉间的差异有无显著性（α=0.05）？表2 长跑锻炼前后的晨脉数、差值及其秩次序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 前70 76 56 63 63 56 58 60 65 65 75 66 56 59 70 后46 54 60 64 48 55 54 45 51 48 56 48 64 50 54 差值22 22 -4 -1 15 1 4 15 14 17 19 18 -8 9 16 秩次14.5 14.5 –3.5 –1.5 8.5 1.5 3.5 8.5 7 11 13 12 -5 6 101.3 用spss对两相关样本进行非参数检验spss软件包的Nonparametric Tests过程为两相关样本通常提供了3种非参数检验方法，它们是：Sign 检验，用于对两相关样本的总体做符号检验。

10_非参数检验

10_非参数检验

第三节 完全随机化设计多组独立样本 的秩和检验
例10-5 某研究者欲研究A、B两个菌种对小 鼠巨噬细胞吞噬功能的激活作用，将60只 小鼠随机分为三组，其中一组为生理盐水 对照组，用常规巨噬细胞吞噬功能的监测 方法，获得三组的吞噬指数，试比较三组 吞噬指数有无差别？
23
表10-5 不同菌种对小鼠巨噬细胞的吞噬指数
第八章
基于秩次的非参数检验
1
参数与非参数统计方法
参数统计（parametric statistics） 例如：t 检验和方差分析。
非参数统计（nonparametric statistics） 例如：秩和检验（rank sum test）。
2
非参数检验的适用场合：
1. 样本来自的总体分布形式未知； 2. 不能或未加精确测量的资料，如等级资料；
例10-1 某研究者欲研究保健食品对小鼠抗 疲劳作用，将同种属的小鼠按性别和年龄相 同、体重相近配成对子，共10对，并将每对 中的两只小鼠随机分到保健食品两个不同的 剂量组，过一定时期将小鼠杀死，测得其肝 糖原含量（mg/100g），结果见表10-1， 问 不同剂量组的小鼠肝糖原含量是否不同？
5
3. 某些分组数据一端或两端是不确定值的；
4. 参数检验条件得不到满足的，如非正态资料、
样本例数较少分布类型显示不清的资料、不能
进行数据转换的资料。
3
第一节
配对设计和单样本资料的 符号秩和检验
1. 配对设计资料的符号秩和检验 ； 2. 一组样本资料的符号秩和检验 。
4
一、配对设计资料的符号秩和检验
=0.05
2．编秩 均秩次。
将各组数据混合，由小到大排序并编秩，如遇有相等数值则取平

卫生统计学第八版李晓松第十章基于秩的非参数检验

卫生统计学第八版李晓松第十章基于秩的非参数检验

第一节 配对样本的比较
（一）单样本数据的符号秩和检验
基本思想 1.假设样本所对应的总体中位数与给定的总体中位数相同，H0：M1 = M0。 2.计算样本中所有数值与给定中位数的差值，根据所有差值绝对值进行编 秩，得到正差值的秩和R+和负差值的秩和R-。
n(n +1) 3.若H0成立，理论上，R+与R-的总体均数应相等，等于： R ，总体 4 n(n 1)(2n 1) 标准差也应相等，等于： R 。 24 4.若R+与R-相差悬殊，均远离M0，则有理由拒绝H0 。具体通过R+ 或R- 的
第二节 两组独立样本的比较
（一）两组定量数据的比较
12岁男童与女童发样中Ca含量(μg/g)的比较 男童 Ca含量（1） 秩（2） 1843 18 383 4 406 5 334 1 443 6 676 11 771 13 358 3 607 9 484 7 n1=10 R1=77 女童 Ca含量（3） 秩（4） 842 14 336 2 742 12 1367 15 1623 16 597 8 1976 19 1818 17 643 10 4534 20 n2=10 R2=133
第一节 配对样本的比较
（二）配对样本数据的符号秩和检验
检验步骤
(1) 建立检验假设，确定检验水准 H0：差值的总体中位数等于0， Md = 0 H1：差值的总体中位数不等于0， Md ≠ 0
=0.05
(2) 求差值、编秩、求秩和
首先计算每对数据的差值，并对差值进行编秩。分别计算正、负差
值的秩和，得出 R+与R- ，如表所示。
第二节 两组独立样本的比较
（一）两组定量数据的比较
基本思想

非参数检验的方法

非参数检验的方法

非参数检验的方法
嘿，你知道非参数检验吗？这可是个超厉害的统计方法呢！非参数检验不需要对总体分布做出假设，哇，这多牛啊！那它的步骤是啥呢？先确定研究问题和数据，然后选择合适的非参数检验方法，比如秩和检验啥的。

接着计算检验统计量，最后根据统计量做出决策。

这听起来是不是挺简单？但可别小瞧哦，这里面也有不少要注意的地方呢。

比如数据得独立、随机，不然结果可就不靠谱啦。

那非参数检验安全不？稳定不？嘿，放心吧！它一般都挺安全稳定的，不会像有些方法那样容易出幺蛾子。

非参数检验都啥时候用呢？当数据不满足参数检验条件的时候呗。

比如数据严重偏态，或者分布不明，这时候非参数检验就大显身手啦。

它的优势可不少呢，对数据分布要求低，适用范围广，多棒啊！就好比你去参加一场比赛，参数检验就像有很多严格规则的项目，非参数检验呢，就像那种规则比较灵活的，不管你啥情况都能玩得转。

给你举个实际案例吧。

比如说有两组病人的康复时间数据，不知道是不是有差异。

用非参数检验一分析，哇，发现真的有明显不同呢。

这效果多好啊！非参数检验就是这么厉害，在很多情况下都能帮我们解决问题。

它就像一个万能工具，随时准备为我们服务。

所以啊，非参数检验真的很不错，值得我们在数据分析中好好利用。

非参数检验的概念与过程

非参数检验的概念与过程

非参数检验的概念与过程导言在统计学中，非参数检验是一种不依赖于总体分布假设的方法，用于对数据进行统计推断。

与参数检验相比，非参数检验更加灵活，适用于各种数据类型和样本量的情况。

本文将介绍非参数检验的基本概念及其应用过程。

什么是非参数检验？在传统的统计推断中，我们通常需要假设数据的总体分布满足某种特定的参数化模型（如正态分布）。

然而，在实际应用中，我们并不总是了解或能够准确描述数据的分布。

此时，非参数检验成为一种有力的工具。

非参数检验不依赖于总体分布的假设，而是在不对数据做过多假设的情况下，通过对样本数据的排序、秩次转换等操作，进行统计推断。

非参数检验的应用场景非参数检验广泛应用于多个领域，特别是当数据不满足参数化分布假设时。

下面列举几个常见的应用场景：1. 样本量较小在样本量较小的情况下，参数化方法可能对数据分布的假设过于苛刻，导致结果不够准确。

而非参数检验则不对数据分布做过多要求，能够更灵活地处理小样本数据。

2. 数据不满足正态分布假设正态分布假设是很多参数检验方法的基础前提。

但在实际问题中，数据往往并不服从正态分布。

非参数检验不需要对数据做分布假设，因此更适用于处理不满足正态分布假设的数据。

3. 数据有序或等级性质对于无法直接度量或比较数值大小的数据，如排名数据、生活满意度评价等，非参数检验提供了一种适用的方法。

通过对数据的秩次进行比较，我们可以推断出两组数据是否存在显著差异。

非参数检验的基本过程非参数检验通常包括以下几个基本步骤：1. 建立原假设和备择假设在进行非参数检验之前，我们需要明确所研究的问题，并建立原假设（H0）和备择假设（H1）。

原假设通常是指两组样本没有显著差异，而备择假设则相反。

2. 选择合适的非参数检验方法根据实际问题和数据类型的特点，选择合适的非参数检验方法。

常用的非参数检验方法包括Wilcoxon秩和检验、Mann-Whitney U检验、Kruskal-Wallis单因素方差分析等。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第10章非参数检验平时我们使用的统计推断方法大多为参数统计方法，它们都是在已知总体分布的条件下，对相应分布的总体参数进行估计和检验。

比如单样本u检验就是假定该样本所在总体服从正态分布，然后推断总体的均数是否和已知的总体均数相同。

本节要讨论的统计方法着眼点不是总体参数，而是总体分布情况，即研究目标总体的分布是否与已知理论分布相同，或者各样本所在的分布位置/形状是否相同。

由于这一类方法不涉及总体参数，因而称为非参数统计方法。

SPSS的Nonparametric Tests菜单中一共提供了8种非参数分析方法，它们可以被分为两大类：1、分布类型检验方法：亦称拟合优度检验方法。

即检验样本所在总体是否服从已知的理论分布。

具体包括：Chi-square test：用卡方检验来检验二项/多项分类变量的几个取值所占百分比是否和我们期望的比例有没有统计学差异。

Binomial Test：用于检测所给的变量是否符合二项分布，变量可以是两分类的，也可以使连续性变量，然后按你给出的分界点一分为二。

Runs Test：用于检验样本序列随机性。

观察某变量的取值是否是围绕着某个数值随机地上下波动，该数值可以是均数、中位数、众数或人为制定。

一般来说，如果该检验P值有统计学意义，则提示有其他变量对该变量的取值有影响，或该变量存在自相关。

One-Sample Kolmogorov-Smirnov Test：采用柯尔莫哥诺夫-斯米尔诺夫检验来分析变量是否符合某种分布，可以检验的分布有正态分布、均匀分布、Poission 分布和指数分布。

2、分布位置检验方法：用于检验样本所在总体的分布位置/形状是否相同。

具体包括：Two-Independent-Samples Tests：即成组设计的两独立样本的秩和检验。

Tests for Several Independent Samples：成组设计的多个独立样本的秩和检验，此处不提供两两比较方法。

Two-Related-Samples Tests：配对设计的两样本秩和检验。

Tests for Several Related Samples：配伍设计的多样本秩和检验，此处同样不提供两两比较。

一、分布位置检验方法1、Two Independent Samples Test与 K Independent Samples Test用于检验两独立样本/多独立样本所在总体是否相同。

Two-lndependent-Samples Test对话框:(1)Test Variable框，指定检验变量。

(2)Grouping Variable框，指定分组变量。

Define Groups对话框，Groupl 和Groupl后的栏中，可指定分组变量的值。

(3)TestType框，确定用来进行检验的方法。

Mann-Whitney U：默认值，相当于两样本秩和检验。

Kolmogorov-Smimov Z：K-S检验的一种。

Moses extreme reactions：如果施加的处理使得某些个体出现正向效应，而另一些个体出现负向效应，就应当采用该检验方法。

Wald-Wolfowitz runs：游程检验的一种，检验总体分布是否相同。

(4)Options对话框，选择输出结果形式及缺失值处理方式。

多个独立样本检验中不同之处：Define Range对话框，定义分组变量值范围。

Minimum:分组变量范围的下限。

Maximum:上限。

Test Type框，确定用来进行检验的方法。

Kruskal-WallisH：默认值，单向方差分析，检验多个样本在中位数上是否有差异； Median：中位数检验，检验多个样本是否来自具有相同中位数的总体。

2、Two Related Samples Test与 K Related Samples TestTwo Related Samples Test是考察配对样本的总体分布是否相同，或者说差值总体是否以0为中心分布；K Related Samples Test则用于检验多个配伍样本所在总体的分布是否相同。

Two-Related-SamplesTests对话框：(1)Test Pair(s)List框，指定检验变量对。

可有多对。

(2)TestType框，确定检验的方法。

Wilcoxon：默认值，配对设计差值的秩和检验，利用次序大小。

Sign：符号检验，利用正负号。

McNemar：配对卡方检验，适用于两分类资料，特别适合自身对照设计。

Marginal Homogeneity：适用于资料为有序分类情况。

(3)Options对话框中，选择输出结果形式及缺失值处理方式，K Related SamplesTest 用于多组间的非参数检验，不同之处在于：A、比较方法不同：☆ Friedman：系统默认值，即最常用的随机区组设计资料的秩和检验，也被称为M检验。

☆ Kendall's W：该指标也被称为Kendall和谐系数，它表示的是K个指标间相互关联的程度(一致性程度)，取值在0～1之间。

☆ Cochrarl's Q：是两相关样本McNemar检验在多样本情形下的推广，只适用于二分类变量。

B、Statistics对话框: Descriplive，描述统计量。

Quartiles，四分位数。

二、分布类型检验方法原理：计算实际分布与理论分布间的差异，根据某种统计量求出P值。

1、Chi-square test与行×列表卡方检验区别：Chi-square test是检验分类数据样本所在总体分布（各类别所占比例）是否与已知总体分布相同，是一个单样本检验。

行×列表卡方检验是比较两个分类资料样本所在的总体分布是否相同，在spss中要用crosstable菜单来完成。

具体做法：先按照已知总体的构成比分布计算出样本中各类别的期望频数，然后求出观测频数与期望频数的差值，最后计算出卡方统计量，利用卡方分布求出P 值，得出检验结论。

例5.1 某地一周内各日死亡数的分布如表所示，请检验一周内各日的死亡危险性是否相同？周日一二三四五六日死亡数 11 19 17 15 15 16 19数据文件为death.sav：day 周日，death 死亡数。

Chi-Square Test对话框：(1)Test Variable List框，指定检验变量，可为多个变量。

(2)ExpectedRange栏，确定检验值的范围。

Get from data选项，即最小值和最大值所确定的范围，系统默认该项。

●Use specified range选项，只检验数据中一个子集的值，在Lower和Upper 参数框中键入检验范围的下限和上限。

(3)ExpectedValues栏，指定期望值。

●All categories equal选项，系统默认的检验值是所有组对应的期望值都相同，这意味着你要检验的总体是否服从均匀分布。

●Values选项，选定所要检验的与总体是否服从某个给定的分布，并在其右边的框中键人相应各组所对应的由给定分布所计算而得的期望值。

“Add”按钮，增加刚键入的期望值，必须大于0。

“Remove”按钮，移走错误值。

“Change”按钮，替换错误值。

（4）Options对话框。

A、Statistics栏，选择输出统计量。

Descriptive：输出变量的均值、标准差、最大值、最小值、非缺失个体的数量。

Quartiles 复选项，输出结果将包括四分位数的内容。

显示第25、50与75百分位数。

B、在MissingValues栏中选择对缺失值的处理方式。

具体操作如下：Data →Weight Case → Weight Case by:→ Frequency Variable: death→OK；Analyze→Nonparametic Test→Chi-Square→Test variable list：day→OK。

卡方值X2=2.875，自由度(DF)=6，P=0.824，可认为一周内各日的死亡性是相同的。

2、Binomial Test（二项分布检验）调用Binomial过程可对样本资料进行二项分布分析，检验二项分类变量是否来自概率为P的二项分布。

例5-2 某地某一时期内出生40名婴儿，其中女性12名(Sex=0)，男性28名(sex=1)。

问该地出生婴儿的性比例与通常的男女性比例(总体概率约为0.5)是否不同?数据文件为sex.sav。

Binomial Test对话框：(1)Test Variable框，指定检验变量。

(2)Define Dichotomy栏，定义二分值。

●Get from data选项，适用于指定的变量只有两个有效值，无缺失值。

●Cut point选项，如果指定的变量超过两个值，选择该项，并在参数框中键入一个试算点的值。

(3)Test参数框，指定检验概率值。

默认的检验概率值是0.5，这意味着要检验的二项是服从均匀分布的。

(3)Options对话框，选择输出结果形式及缺失值处理方式。

具体操作如下：Binomial TestTest → Test Variable List →sex→ Test Proportion →0.50→OK。

二项分布检验表明，女婴12名，男婴28名，观察概率为0.7(即男婴占70%，检验概率为0.5，二项分布检验的结果是双侧概率为0.018，可认为男女比例的差异有高度显著性，即与通常的0.5的性比例相比，该地男婴比女婴明显多。

3、Runs Test（游程检验）一个游程是指某序列中同类元素的一个持续的最大主集，或者说一个游程是指依时间或其他顺序排列的有序数列中，具有相同的事件或符号的连续部分。

游程检验用于检验样本或任何序列的随机性。

例5-3 某村发生一种地方病，其住户沿一条河排列，调查时对发病的住户标记为1，非发病住户为0，共26户，如下表所示。

0 1 1 0 0 0 1 0 0 1 0 O 0 0 1 1 O 01 0 0 0 0 1 0 l数据文件为run.sav：住户变量为epi。

Runs Test 对话框：(1) Test Variable框，指定检验变量。

(2) Cut Point栏，确定划分二分类的试算点。

中位数、众数、均数及用户指定临界割点。

(3) Options对话框，选择输出结果形式及缺失值处理方式。

具体操作如下：Runs Test → Test Variable →epi→1→ OK从检验结果可见，本例游程个数为14，小于1有17个案例；而大于或等于1有9个案例。

Z=0.325，双尾检验概率P＝0.746。

所以认为此地方病的病户沿河分布的情况无聚集性,而是呈随机分布。

4、单样本K-S检验又称单样本柯尔莫哥洛夫-斯米诺夫检验(one-sample Kolmogorov-Smirmov tes)。