第6讲量子场论
- 格式:ppt
- 大小:1.72 MB
- 文档页数:68

量子场论课程教学大纲一、课程说明(一)课程名称、所属专业、课程性质、学分;课程名称:量子场论所属专业:理论物理课程性质:专业课学时:72学分:4(二)课程简介、目标与任务;近一个世纪以来,量子场论一直是了解微观世界的重要工具,是粒子物理的重要理论基础,并已广泛应用于微观物理其他领域。
场的量子化解释了场与粒子之间的内在联系,而量子场论合理地描述了粒子的产生、湮灭,及其相互转化现象。
上世纪五十年代初建立的体系完整的量子电动力学(QED),是关于带电粒子、光子及其相互作用的量子场论,是U(1)的阿贝尔规范场理论。
光子的辐射与吸收、光电效应、Compton 散射,特别是氢原子的Lamb移动、电子磁矩的计算与实验的精确符合等,足以说明量子电动力学的正确性。
此外,量子电动力学中建立的重整化理论也是成功的。
弱电统一理论克服了过去四个费米子直接相互作用理论不能重整化的困难;预言了中性流并得到严格的实验支持;中微子、反中微子与核子和电子碰撞等过程与实验符合得很好。
在强相互作用领域,上世纪七十年代发展和建立的量子色动力学(QCD)是SU(3)非阿贝尔规范理论,它是1954年杨振宁建立的SU(2)非阿贝尔规范理论的推广。
由量子色动力学探讨核子之间相互作用的严格理论目前尚未解决。
基本粒子之间的电磁相互作用、弱相互作用、强相互作用都是由规范理论建立起来的,三种相互作用是由三类规范玻色子传递的。
量子场论就是研究以三代轻子和三代夸克作为基本粒子,以强子夸克模型和弱电统一理论与量子色动力学为基础的标准模型。
量子场论(一)主要研究量子电动力学。
(三)先修课程要求,与先修课与后续相关课程之间的逻辑关系和内容衔接;分析力学、电动力学、量子力学(四)教材与主要参考书。
量子场论,段一士,高等教育出版社,2015年二、课程内容与安排第一章绪论(4学时)1.1 组成物质的基本粒子,轻子和夸克1.2 量子场论、规范场论和规范玻色子1.3 自然单位经典场论(20学时)2.1 广义洛伦兹变换2.2 张量2.3 标量场方程2.4 矢量场方程2.5 γ矩阵2.6 旋量(四元旋量)2.7 旋量场方程2.8 二分量中微子理论2.9 单位旋量的一些性质和正反粒子投影算符2.10 场论中的Lagrange原理2.11 经典场论中的广义守恒定理、Noether定理2.12 能量动量张量和能量动量守恒2.13 角动量张量与角动量守恒2.14 电流密度矢量和电荷守恒定律第三章自由场量子化(24学时)3.1 二次量子化的基础和量子场论的基本假设3.2 Schrodinger表象和Heisenberg表象3.4 实标量场量子化3.5 复标量场量子化3.6 矢量场量子化3.7 旋量场量子化3.8 场方程的Green函数和Feynman函数3.9 N 乘积, P 乘积和T 乘积第四章场的相互作用与S矩阵(24学时)4.1 场的相互作用拉格朗日函数4.2 场在相互作用情况下的运动方程与相互作用哈密顿4.3 相互作用表象4.4 U(t, t_0) 矩阵和它的4.5 S矩阵的定义和它在量子电动力学中的形式4.6 T乘积展开的Wick定理和S矩阵的展开式4.7 S矩阵的Feynman图解4.8 Furry关于电子封闭内线的定理4.9 S矩阵的矩阵元4.10 S矩阵元的动量表象4.11 基本粒子反应几率和截面4.12 光子或电子的自旋状态的求和与平均的公式4.13 在非相对论情况下的Rutherford散射问题4.14 光子和电子的散射(Compton效应)4.15 正负电子对湮灭为两个光子4.16 高能电子对撞反应4.17 μ粒子衰变(一)教学方法与学时分配教学方法以讲授为主。



量子力学与量子场论研究作者:刘乐来源:《科技视界》2014年第30期【摘要】本文介绍并分析了量子力学与量子场论的主要内容,对相关理论进行了探讨和研究。
【关键词】量子力学;量子场论;研究量子理论为现代物理学提供了新的关于微观物理世界的思考方法和表述方法,对固定物理学、原子物理学、粒子物理学以及核物理学的发展奠定了理论基础。
量子理论的发展经历了旧量子论、量子力学、量子场论三个重要阶段,为我们从微观层面理解宏观现象提供了理论基础。
1 量子力学量子力学是物理学的分支学科,主要研究微观粒子的运行规律,与相对论一起构成了现代物理学的两大基本支柱。
量子力学是在普朗克的量子假说、玻尔的原子理论以及爱因斯坦的光量子理论等旧量子论基础上发展起来的,根据量子态理论,经典物理量的量子化问题可以归结为薛定谔波动方程的求解问题:1.1 量子矩阵力学矩阵力学是量子力学的一种表现形式,是由海森堡博士于1925年提出的,用辐射频率和强度等光学等可观察的量来取代电子轨道概念以及有关经典运动学的量,将参与跃迁过程的状态量排成矩阵并引入方程,从而得到一种不同于y·x的x·y不可对易代数,海森堡博士以相对简单的线性谐振子作为矩阵力学的支撑点,试图只用光谱线的频率、强度、偏极化等来观察电子在原子中的轨道,这显然受到了爱因斯坦相对论中对空间和时间作“操作定义”分析的影响。
矩阵力学呈现的内容可以概括为四点:用厄米特矩阵表示任何物理量,其中也包括哈密顿量;坐标矩阵X和动量矩阵Px满足一定的对易关系(PxX__XPx=-ihE);系统的正则运动方程是X=[X,H],Px=[Px,H];物理系统的光谱线频率hvmn=Emm-Enn决定(Emm为H的本征值)。
1.2 量子波动力学奥利利理论物理学家薛定谔对物理学最大的贡献就是独立创立了量子波动力学,并提出了薛定谔方程,薛定谔方程是量子力学中用来描述运动速度远比光速小的微观粒子(如电子、质子、中子等)运动状态的基本规律,这种波动方程与海森堡博士的矩阵描述是等价的。

精心整理第一章预备知识§1粒子和场以现有的实验水平,确认能够以自由状态存在的各种最小物质,统称为粒子。
电子、光子、中子、质子等是最早认识的一批粒子,陆续发现了大量的粒子、介子和共振态,粒子的数目达数百种,它们是物质存在的一种形式。
电磁相互作用的强度是以精确结构常数2317.2973104137.036e cαπ-===⨯来表征的,可以同时参与四种相互作用的粒子(例如质子p)为代表,通过典型的反应过程的比较研究,确定各种作用强度的大小。
2.粒子的属性不同粒子有不同的内禀属性,这些属性不因粒子产生的来源和运动状态而改变。
持不变,粒子具偶宇称(P=1)。
粒子的性质,可查阅有关资料。
例如:ParticleDataGroup编的ReviewofParticlePhysics,刊登于Plys.Lett.B592(2004)。
3.粒子的分类可按多种方式对粒子分类。
按参与相互作用的性质,可分为三类:(a)强子,既参与强相互作用,也参与弱相互作用。
已发现的粒子大多数是强子,包括重子,介子。
(b)轻子,不参与强相互作用的粒子,有的参与电磁作用和弱作用,如电(a)规范玻色子,传递相互作用的粒子(b)费米子,包括轻子和夸克(c) Higss粒子,按弱电统一理论,应该有存在有自旋为0的Higss粒子,但实际上至今未发现。
按此理论分类,有两个实验上未解决的问题,一是夸克禁闭,还找不到自由夸克,二是Higss 粒子还未找到。
按粒子的自旋分类.(a)自旋s=0的粒子,称标量粒子,如π,k 介子等 (b)自旋21=s 的粒子,称旋量粒子,如电子e 、质子p 等普朗克常数:s J h⋅⨯==-3410)18(05457168.12πs Mev ⋅⨯=-2210)56(58211915.6量纲ET = dim(数据来自Pyhs.LettB592.91(2004)).建立一个在微观邻域应用方便的新单位制,规定这三个量的值为无量纲的1,即 这样在这一单位制中,量纲关系为:dimc=11-=T Ldimk=1KE=dimh=11-E=T即LE==-1,只剩一个独立的量纲。

初学《量子场论》在科大这一年代培生活即将结束,我学习《量子场论》的进程也要告一段落。
唯一的遗憾是今后的研究方向不是场论。
也许我的同学对我的建议是有道理的:应该把所学的理论在计算机编程上加以实现,尤其对于那些分子数目较多的体系。
这一学年,我也仅仅是对场论中的QED部分有了了解,可以说是入门吧。
总的感觉就一个:delicate。
它的精确程度超过了经典物理中的任何一个分支,它的结果比Maxwell的电磁理论还要优美!它将狭义相对论和量子力学很自然的结合在了一起:协变性,不确定性,对称性,绘景变换,微扰论,产生湮灭算符等在这个理论框架下得到了完美的体现。
一般说来,进入量子场论有正则量子化和路径积分两种方式,不过大伙儿都偏向于前者(提供了一个和经典理论对比的平台)。
实际上后者更为自然。
1.对称性这是基本上是场论中的开场白-Noether定理-将场的作用量和无穷小连续变换结合在了一起。
大多数教科书一般是从自由多分量标量场的形式入手,结合变分原理,从时空平移对称性,时空各向同性,内部对称性,整体规范对称性得到对应的表达式,并将它们作为自由场相应物理量的定义式。
这是类比于经典的做法。
但这样有个不好的地方,就是如何知道这样得出的式子能应用于量子情况而不出现异常。
实际上这套理论是自洽的。
或许可以接受另外的一套途径:从群论的角度找到幺正变换的无穷小生成元满足的性质(如Weinberg),然后通过经典的形式构造相应的物理量,结合场的对易关系去验证合理性。
另一部分的重要内容是要得出场算符和幺正变换的关系式。
要注意的是,场算符不同于量子力学中算符:量子力学中的算符带有坐标变量,那是因为一个抽象的算符选取了坐标表象而得出的;而在场论中,没有坐标表象一说,场算符带有坐标参数是本身的性质--在时空每一点都定义了一个操作。
现在,唯一知可以利用的就是经典标量函数,矢量函数等的变换规律和场算符的性质。
得到量子场算符变换规律最好的阐述是Bailin, Love的《Gauge field theory》中一个很漂亮的式子:从它可以导出变换法则。

量子场论概论量子场论(Quantum Field Theory)是现代物理学中最基础的理论之一,它描述了宏观世界中的粒子是如何由场产生和相互作用的。
量子场论结合了量子力学和狭义相对论,是粒子物理学研究的核心理论之一。
本文将为读者提供量子场论的概要介绍。
一、量子场的基本概念量子场论的起点是量子力学中的波函数,而在量子场理论中,波函数被替代为场。
场是时空中的实数或复数函数,它的不同取值代表了不同的粒子状态。
量子场满足薛定谔方程或者狄拉克方程,这些方程描述了场随时间和空间的演化规律。
二、量子场的量子化量子场论的目的是将场量子化,即将经典的场变量转化为算符,使之符合量子力学中的对易或反对易关系。
这样,场就成为了多粒子态的产生算符和湮灭算符的叠加。
量子场的运动方程可以通过拉格朗日量推导得到。
三、量子场的相互作用量子场之间的相互作用可以通过相互作用项来实现,相互作用项是拉格朗日量中的一部分。
在相互作用的过程中,场可以相互转化成不同的粒子,这也是量子场论的特殊之处。
通过计算相互作用过程的概率振幅,可以得到不同粒子的散射截面等物理量。
四、量子场论的重整化量子场论中的计算过程中会遇到发散的问题,这些发散可以通过重整化来处理。
重整化是一种数学技巧,通过重新定义物理量的取值,将发散项与物理量的实际观测结果相抵消。
重整化为量子场论提供了可计算的结果。
五、量子场论的应用量子场论在粒子物理学中有广泛的应用。
它被用于描述基本粒子之间的相互作用,如强相互作用、弱相互作用和电磁相互作用。
量子场论也被用于解释和预测实验结果,揭示物质的微观结构。
六、前沿问题与展望量子场论在理论物理学中仍然存在许多未解决的问题和待探索的领域。
例如,引力场的量子化是理论物理学的一大难题。
量子场论在宇宙学和黑洞物理学等领域也有着重要的应用和深刻的启示。
总结:量子场论是描述粒子之间相互作用的重要理论,它将量子力学和狭义相对论相结合,给出了精确的物理描述。
通过量子场的量子化和相互作用的计算,我们可以得到不同粒子的性质和相互作用过程的概率。

量子场论的基本概念量子场论是理论物理学中的一门重要学科,它是量子力学和场论的结合体,用于描述微观粒子的行为和相互作用。
本文将介绍量子场论的基本概念,包括场的概念、量子化、费曼图等内容。
一、场的概念在经典物理学中,我们通常用场来描述物质的分布和运动。
而在量子场论中,场被看作是一种物质的激发态,它可以被量子化,即将其视为一系列的量子振动。
量子场论中的场可以是标量场、矢量场或旋量场等不同类型。
二、量子化量子场论的核心思想是将场量子化,即将场视为一系列的量子振动。
量子化的过程可以通过将场展开为一系列的谐振子来实现。
每个谐振子对应一个量子态,其能量由频率决定。
通过对谐振子的量子化,我们可以得到场的量子态和相应的能谱。
三、费曼图费曼图是量子场论中的重要工具,用于描述粒子的相互作用过程。
费曼图由线和顶点组成,线表示粒子的传播,顶点表示粒子的相互作用。
通过费曼图,我们可以计算粒子的散射截面和衰变速率等物理量。
四、量子场论的基本方程量子场论的基本方程是量子场的运动方程,通常采用拉格朗日量的形式。
拉格朗日量包含了场的动能项和相互作用项,通过变分原理可以得到场的运动方程。
解场的运动方程可以得到场的量子态和相应的能谱。
五、量子场论的应用量子场论在粒子物理学中有广泛的应用。
例如,标准模型是一种基于量子场论的理论,用于描述基本粒子的相互作用。
量子场论还可以用于计算粒子的散射截面、衰变速率等物理量,从而与实验结果进行比较。
六、量子场论的发展量子场论是一个非常活跃的研究领域,不断有新的理论和方法被提出。
例如,超对称量子场论是一种扩展的量子场论,它可以解决一些标准模型中存在的问题。
另外,量子场论与引力的统一也是一个重要的研究方向。
总结:量子场论是理论物理学中的一门重要学科,它将量子力学和场论相结合,用于描述微观粒子的行为和相互作用。
量子场论的基本概念包括场的概念、量子化、费曼图等内容。
通过量子场论,我们可以计算粒子的散射截面、衰变速率等物理量,并与实验结果进行比较。
第一章 预备知识§1 粒子和场以现有的实验水平,确认能够以自由状态存在的各种最小物质,统称为粒子。
电子、光子、中子、质子等是最早认识的一批粒子,陆续发现了大量的粒子、介子和共振态,粒子的数目达数百种,它们是物质存在的一种形式。
场是物质存在的另一种形式,这种形式主要特征在于场是弥散于全空间的,全空间充满着各种不同的场,它们互相渗透和相互作用着。
按量子场论观点,每一种粒子对应一种场,场的激发表现为粒子的出现,不同激发态表现为粒子的数目和状态不同,场的退激发,表现为粒子的湮沒。
场的相互作用可以引起激发态的改变,表现为粒子的各种反应过程,也就是说场是物质存在的更基本的形式,粒子只是场处于激发态时的表现。
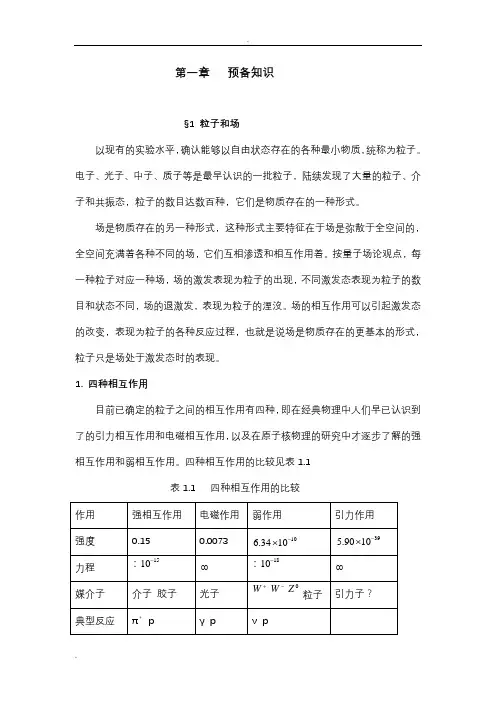
1. 四种相互作用目前已确定的粒子之间的相互作用有四种,即在经典物理中人们早已认识到了的引力相互作用和电磁相互作用,以及在原子核物理的研究中才逐步了解的强相互作用和弱相互作用。
四种相互作用的比较见表1.1 1010介子 胶子Z W W -+电磁相互作用的强度是以精确结构常数2317.2973104137.036e cαπ-===⨯来表征的,可以同时参与四种相互作用的粒子(例如质子p )为代表,通过典型的反应过程的比较研究,确定各种作用强度的大小。
2. 粒子的属性不同粒子有不同的内禀属性,这些属性不因粒子产生的来源和运动状态而改变。
最重要的属性有:质量m ,粒子的质量是指静止质量,以能量为单位,它和能量E 和动量→P 的关系为42222c m c p E =-电量Q ,粒子的电荷是量子化的,电荷的最小单位是质子的电荷。
自旋S ,粒子的自旋为整数或半整数,如π介子的自旋为0,电子的自旋为1/2 ,矢量介子的自旋为1。
平均寿命τ,粒子从产生到衰变为其它粒子所经历的时间称为粒子的寿命。
由于粒子的寿命不是完全确定值,具一定的几率分布,如果0N 个相同粒子进行衰变,经过时间t 后还剩下N 个,则teN N τ10-=,式中τ即为粒子的平均寿命。

相对论知识:量子场论的相对论解释随着科学技术的不断发展,人类对于自然世界的认知也不断深入。
相对论和量子力学是现代物理学两个最为成功、最基础的理论,它们分别描述了大尺度和小尺度下的物理现象。
但是这两个理论之间依然存在许多困扰人们的问题,比如,如何在描述电子、光子等微观粒子时,让相对论和量子力学两个理论相一致。
这个问题的解决就是quantum field theory(量子场论),它提供了一种非常有力的框架来解决理论上和实际上的问题。
本文将要探讨一下量子场论的相对论解释。
量子场论的基础概念量子场论是一种描述基本粒子和相互作用的理论。
在量子场论中,粒子不再是“点”,而是由量子场产生的涟漪。
量子场的量子激发称为粒子,例如光子、电子、夸克等。
一个量子场包含许多粒子,这些粒子描述了场的激发。
这就是著名的波粒二象性。
在量子场论中,场具有几个重要的性质。
首先,量子场是不断涟漪、变化的,其状态存在好几种可能性。
第二,我们可以看成空间中每一个点都存在一个量子场的振幅。
每个点相互之间不断地相互作用,形成了一个“场”。
第三,由于量子力学的规定,任何一个量子系统的真实状态都必须用波函数来描述。
在量子场论中,波函数就如同一个浪,涟漪的形状能够反映场的状态。
我们知道,完整的量子力学包括海森堡矩阵力学和薛定谔波动力学。
海森堡矩阵力学更注重于应变和关联,而薛定谔波动力学更注重于空间和时间波动。
量子场论可以看作两者的结合体,因为它结合了空间和时间,并描述了应变和关联。
相对论的基础概念相对论是描述高速而非高密度物理系统中运动的自然定律的理论。
相对论有两个基本原理:相对性原理和光速不变原理。
其中,相对性原理指出物理定律在所有惯性参考系中都是相同的;光速不变原理指出光速在任何惯性参考系中都是相同的。
就是说,光速是一个普适常数,独立于观察者自身的速度和空间位置。
相对论中的相对论效应都是非常小的,除了“光速不变”的规律外,它们通常只有高速度或强引力场中才能显示出来。
量子场论深度科普量子场论是理论物理学中的一门重要学科,它是量子力学和场论的结合体,用于描述微观粒子的行为。
本文将深入科普量子场论的基本概念和原理。
一、量子场论的基本概念量子场论是由量子力学和经典场论演化而来的,它的基本思想是将粒子看作是场的激发态。
在量子场论中,每种粒子都对应着一个场,而场的激发态则对应着粒子的存在。
二、量子场的本质量子场是一个能够在空间中传播的物质或能量的载体。
在经典场论中,场是连续的,而在量子场论中,场是离散的,即由许多个量子组成。
这些量子被称为粒子。
三、量子场的量子化量子场论通过对场的量子化来描述粒子。
量子化是指将经典场变为量子场的过程。
具体而言,量子化过程中,通过引入产生算符和湮灭算符来描述粒子的产生和湮灭。
四、量子场论的运动方程量子场论中的场满足一种称为场的运动方程的物理规律。
这个方程可以通过作用量原理导出。
量子场的运动方程描述了场的演化规律。
五、量子场论的拉格朗日量在量子场论中,拉格朗日量是描述系统动力学的关键。
拉格朗日量包含了场和其导数的信息,通过对拉格朗日量进行变分可以得到场的运动方程。
六、量子场论的相互作用量子场论可以描述不同场之间的相互作用。
相互作用可以通过在拉格朗日量中引入相互作用项来描述。
这些相互作用项可以用来解释粒子之间的相互作用和力的产生。
七、量子场论的重要应用量子场论在现代物理学中有广泛的应用。
它被应用于粒子物理学、凝聚态物理学、量子化学等领域。
量子场论的研究对于理解微观世界的基本规律具有重要意义。
八、量子场论的挑战和问题尽管量子场论是一种非常成功的理论,但它仍然面临一些挑战和问题。
例如,量子场论与引力理论的统一仍然是一个未解决的难题,这是物理学研究的一个重要方向。
总结:量子场论是描述微观粒子行为的重要理论框架,它将量子力学和场论有机结合,通过量子化和相互作用来描述粒子的产生和演化。
量子场论在现代物理学中有广泛的应用,并对理解微观世界的基本规律具有重要意义。
量子场论概述量子场论是现代物理学中非常重要的一个分支,它是描述微观粒子和场相互作用的理论框架。
本文将对量子场论的基本概念和数学形式进行概述,以及该理论在粒子物理学中的应用。
一、量子场论的概念量子场论是基于量子力学和相对论的理论体系,它将物质和辐射视为场的量子化,并用算符描述场的演化和相互作用。
量子场论是量子力学与相对论的统一,能够描述微观粒子和相互作用的运动规律。
二、量子场论的数学形式在量子场论中,我们采用海森堡绘景来描述场和算符。
场是时空坐标的函数,而算符则是这些场的量子化表示。
量子场论使用了二次量子化的方法,将算符表示为产生和湮灭算符的组合,从而确保了粒子数守恒的条件。
三、量子场论的基本原理量子场论的基本原理包括哈密顿量、场的演化方程和相互作用描述。
哈密顿量确定了系统的能量和粒子的动力学规律,场的演化方程描述了场随时间和空间的演化,相互作用描述了场之间的相互作用过程。
四、量子场论的应用量子场论在粒子物理学中有着广泛的应用,特别是在高能物理和强相互作用领域。
通过量子场论,我们可以描述和计算各种基本粒子的产生和湮灭过程,解释和预测粒子的性质和相互作用规律。
五、量子场论的挑战和展望尽管量子场论在粒子物理学中取得了重大成功,但仍存在一些挑战和未解决的问题。
例如,如何处理场的量子化与重整化的问题,以及将量子场论与引力相统一的问题。
未来的研究将继续在这些方向上发展,以期找到更加完整的理论框架。
六、结论量子场论是现代物理学中非常重要的理论体系,它是描述微观粒子和场相互作用的数学形式和方法。
通过量子场论,我们能够深入理解微观世界的规律,并在实验中得到验证。
随着研究的不断深入,量子场论将继续为我们带来新的认识和发现。
以上是对量子场论的概述,介绍了其基本概念、数学形式、基本原理、应用和展望。
量子场论作为现代物理学的重要理论之一,在解释和预测微观粒子的行为和相互作用规律中发挥着重要作用。
希望本文对读者对量子场论有所启发,同时也提醒我们仍有许多挑战和待解决的问题需要进一步的研究和探索。
量子场论预备知识1. 引言量子场论是理论物理学中的一门重要学科,它是描述自然界最基本的相互作用的理论。
量子场论结合了量子力学和特殊相对论,可以描述微观粒子的行为和相互作用。
在现代物理研究中,量子场论已经成为了一种基础工具,被广泛应用于高能物理、凝聚态物理和宇宙学等领域。
本文将介绍量子场论的基本概念和预备知识,包括场的概念、拉格朗日量、哈密顿量以及基本的场方程等内容。
2. 场的概念在经典物理中,我们通常使用质点来描述物体。
然而,在微观尺度上,质点模型变得不再适用。
相反,我们需要引入一个新的概念——场。
场可以看作是空间中某个点上的物理量随时间和空间变化的函数。
在电磁学中,电磁场描述了电荷和电流如何影响周围空间中其他电荷和电流。
在量子力学中,波函数就是一种场。
3. 拉格朗日量拉格朗日量是描述物理系统的一个重要工具。
它是一个关于场和其导数的函数,可以通过最小作用量原理来确定。
在量子场论中,拉格朗日量可以通过对称性和相互作用的要求来确定。
通过选择适当的拉格朗日量,我们可以推导出场方程和相互作用项。
4. 哈密顿量哈密顿量是描述系统能量的函数。
在经典力学中,哈密顿量可以通过拉格朗日变换得到。
在量子场论中,哈密顿量则是通过将拉格朗日密度积分得到。
哈密顿量可以用来计算系统的能级和相互作用强度等物理性质。
通过求解哈密顿量对应的本征值问题,我们可以得到系统的能级结构。
5. 场方程场方程描述了场随时间和空间变化的规律。
在经典物理中,场方程通常由拉格朗日方程推导得到。
在量子场论中,我们使用波动方程来描述场的行为。
波动方程是一个偏微分方程,它描述了场随时间和空间变化满足的基本规律。
通过求解波动方程,我们可以得到场在不同时空点上的取值。
6. 总结量子场论是一门重要的理论物理学科,它描述了微观粒子的行为和相互作用。
本文介绍了量子场论的基本概念和预备知识,包括场的概念、拉格朗日量、哈密顿量以及基本的场方程等内容。
通过学习量子场论,我们可以深入理解微观世界的奥秘,并在现代物理研究中应用这些知识。
量子场论及其应用一、量子场论的基本概念量子场论是描述微观粒子相互作用的理论框架,它将量子力学与相对论的原理相融合,是理论物理学的重要分支。
在量子场论中,将物质和力场都看作量子场,通过场方程和量子化方法来描述它们的运动和相互作用。
量子场论在解释和预言微观现象的过程中具有极高的准确性,被广泛应用于高能物理、凝聚态物理、核物理等领域。
二、量子场论的历史发展量子场论起源于二十世纪二三十年代的量子力学和统计力学的发展。
但当时的理论无法描述相对论性粒子的发射和吸收过程,导致了产生负能态等矛盾。
直到1947年,费曼提出了路径积分方法,为量子场论的建立提供了新的思路。
之后,狄拉克、朗道等学者纷纷为量子场论的发展做出了重要贡献,奠定了现代量子场论的基础。
三、量子场论的数学描述量子场论的数学描述是通过场算符和哈密顿量来实现的。
场算符是对场的量子化描述,可以看作是有无界粒子的产生和湮灭算符。
场算符的演化遵循场方程,如克莱因-戈登方程和狄拉克方程,描述了粒子的运动和相互作用。
哈密顿量则是描述系统的能量和相互作用的算符,可以通过对称性原理来构建,如内禀对称性或者规范对称性。
四、量子场论的应用1. 高能物理学:量子场论在高能物理学中的应用最为广泛。
通过量子场论,研究者可以描述粒子之间的相互作用,预言新的粒子的存在。
例如,标准模型就是一种基于量子场论的理论框架,成功地描述了强、电弱相互作用,并预言了希格斯玻色子的存在,推动了粒子物理学的发展。
2. 凝聚态物理学:量子场论在凝聚态物理学中也有重要应用。
通过量子场论可以描述凝聚态系统中的输运性质、相变、拓扑物态等现象。
例如,拓扑绝缘体的研究就离不开量子场论的工具,通过拓扑的量子场论描述,揭示了新奇的电输运性质。
3. 引力理论:量子场论的应用还可以扩展到引力理论中。
量子场论与广义相对论的结合,产生了量子引力理论,如量子场论中的规范对称性与弦论的研究,为理解宇宙学中的黑洞、暗物质等问题提供了新的思路。