正态分布频率直方图

未知时，以样本标准差 S 代替 σ 所得到的统 计量
xμ S/ n
态分布，而是服从 t 分布(t-distribution)。 它的概率分布密度函数如下：
t 分布概率密度曲线特点: 1、t 分布受自由度的制约，每一个自由度都有一条 t 分布概率密度曲线。 2、t 分布概率密度曲线以纵轴为对称轴，左右对称， 且在t＝0时，取得最大值。 3、与标准正态分布曲线相比，t 分布曲线顶部略低， 两尾部稍高而平。df 越小这种趋势越明显。df 越大，t 分布越趋近于标准正态分布。当n >50时，t 分布与标 准正态分布的区别很小；n >100时，t 分布基本与标准 正态分布相同；n→+∞时，t 分布与标准正态分布完全 一致。
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
x=
1 2
x
-3 -2 -1 0
x=
1 2 3 x
x=
不同均数 均值 反映随机变量的平均水平（位置参数），向 右平移表示逐渐增大，向左平移表示逐渐减小。
（1）曲线在x 轴的上方，与x 轴永不相交 （2）曲线是单峰的,它关于直线 x=μ对称 1 （3）曲线在 x=μ 处达到峰值(最高点) σ 2π （4）曲线与横轴 x所夹面积为1
例3 某地1986年120名8岁男孩身高均数为 X =123.02cm ，标准差为S=4.79cm，试估 计: (1)该地8岁男孩身高在130cm以上者占该地8 岁男孩总数的百分比； (2)身高在120cm～128cm者占该地8岁男孩总 数的百分比; (3)该地80%的男孩身高集中在哪个范围？
t 分布
利用公式，查附表得： (1) P(x＜1.64) =Φ(1.64) =0.9495 (2) P (x≥2.58) =1-Φ(2.58) =1-0.9951 =0.0049 (3) P (│x│≥2.56) =2-2Φ(2.56) =2-2×0.9948 =0.0104 (4) P (0.34＜x≤1.53) =Φ(1.53)-Φ(0.34) = 0.9370-0.6331=0.3039 (5) P(x＜-1.82) =1-Φ(1.82) =1-0.9656 =0.0344

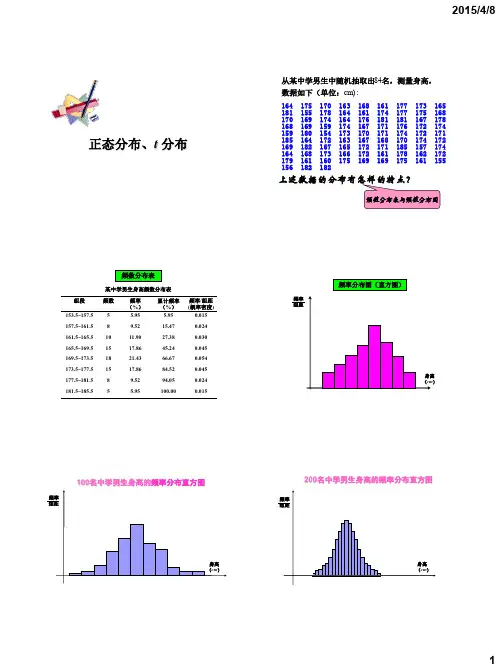
频率分布直方图频率分布直方图是一种通过矩形条形图表达统计数据的方法。

它将变量的范围划分为若干个等宽区间，然后计算每个区间内的观测值频数或频率，并将其绘制成直方图。

直方图可以直观地展示数据的分布情况和集中程度，帮助我们更好地理解数据的特征和趋势。

直方图的绘制步骤通常包括以下几个步骤：1.确定数据的测量尺度：直方图适用于连续变量或有序离散变量，不适用于无序离散变量，因此在绘制直方图之前需要确定数据的测量尺度。

2.确定分组区间数和宽度：根据数据的范围和数量，选择合适的分组区间数和宽度。

通常情况下，分组区间数的选择应该在5到20之间，而宽度的选择应该使得直方图易于理解和分析。

3.计算频数或频率：将数据按照分组区间进行分类，并统计每个区间内的观测值频数或频率。

频数是指数据在每个区间中出现的次数，频率是指频数除以总观测值数的比例。

4.绘制直方图：根据分组区间和对应的频数或频率，绘制矩形条形图。

横轴表示分组区间，纵轴表示频数或频率，每个矩形的宽度表示分组区间的宽度，高度表示频数或频率。

根据直方图的绘制结果，我们可以直观地了解数据的分布情况和集中程度。

例如，如果直方图呈现对称的钟形曲线，说明数据符合正态分布；如果直方图呈现非对称的形状，说明数据分布存在偏态。

通过直方图，我们还可以比较不同组别或不同时间点数据的分布情况，寻找差异和变化趋势。

此外，直方图还可以用于检测异常值和离群点，帮助我们发现数据中的异常情况。

总之，频率分布直方图是一种直观且有效的统计图形，可以帮助我们理解和分析数据的分布情况和集中程度。

通过直方图，我们可以更好地洞察数据的特征和趋势，从而做出更有针对性的决策。

动
f (x)
1

e
(
x )2 2 2
, (

x

)
脑
2π
思
其中 , 是常数，且 ＞0,那么称 服从参数为, 2 的正
考
态分布,简记为 ~ N (, 2 ), 此时 的密度曲线称为正态曲线,
探
称为正态随机变量．
索
新
知
正态曲线具有以下性质（如图所示）；
那么轴的直径尺寸在区间 ( 3 , 3 ) 内取值的概率为
探
索
99.7%．而落在区间 ( 3 , 3 ) 以外的概率只有0.3%．
新 知
这种小概率事件一旦发生，说明生产中可能出现了异常情况，
应该停止生产查明原因，及时采取措施使生产恢复正常．
例4 某灯泡厂生产的白炽灯泡的寿命为 （单位：小时）， 已知 ~ N(1000,30),要保证灯泡的平均寿命为1000小时的概率
兴
［160.5，163.5） 正正63.5，166.5） 正正
10
0.167
导
［166.5，169.5）
3
0.050
入
合计
60
1.000
下面根据这些数据绘制频率分布直方图．
（3）绘制频率分布直方图（如图）
创 设 情 境
兴 趣 导 入
从频率直方图看出，该校16岁女生的身高的分布状况具有“中 间高、两头低”的特点，即身高在157.5cm至160.5cm的人数最多， 往左右两边区间内的人数越少，而且左右两边近似对称．
考
探 索 新 知
设随机变量 ~ N(0，1)．由概率密度曲线的定义知道，任给
区间（-∞，a）， P( a) 的值为下图中阴影部分的面积．

在气象中，某地每年七月份的平均气温、平均湿度 以及降雨量等，水文中的水位；
总之，正态分布广泛存在于自然界、生产及科学技术的许多领域中。
正态分布在概率和统计中占有重要地位。
4、正态曲线的性质
（1）曲线在x轴的上方，与x轴不相交.
（μ－σ，μ＋σ]
0.6826
（μ－2σ，μ＋2σ]
0.9544
（μ－3σ，μ＋3σ]
0.9974
（2）曲线是单峰的,它关于直线x=μ对称.
（4）曲线与x轴之间的面积为1.
（3）曲线在x=μ处达到峰值(最高点)
（5）若 固定, 随 值的变化而沿x轴平移, 故 称为位置参数
（6）当μ一定时，曲线的形状由σ确定 .σ越大，曲线越“矮胖”，表示总体的分布越分散；σ越小，曲线越“瘦高”，表示总体的分布越集中.
5、特殊区间的概率:
m-a
m+a
x=μ
若X~N ,则对于任何实数a>0,概率 为如图中的阴影部分的面积，对于固定的 和 而言，该面积随着 的减少而变大。这说明 越小, 落在区间 的概率越大，即X集中在 周围概率越大。
4
0.04
[0.5,1)
8
0.08
[1,1.5)
15
0.15
[1.5,2)
22
0.22
[2,2.5)
25
0.25
[2.5,3)
14
0.14
[3,3.5)
6
0.06
[3.5,4)
4
0.04
[4,4.5)
2
0.02
11
高尔顿钉板实验的 频率分布直方图
这条曲线具有 “中间高，两头低” 的特征，像这种类型的曲线, 就是（或近似地是）以下函数的图像:

频率分布直方图可以用于 比较不同组别数据的分布 情况，进而进行方差分析 。
风险评估和预测模型构建
风险等级划分
01
在金融、保险等领域中，频率分布直方图可以用于划分风险等
级，评估不同风险水平下的损失分布情况。
预测模型构建
02
在构建预测模型时，频率分布直方图可以帮助确定输入变量的
分布特征，从而选择合适的模型类型和建模方法。
蛋白质表达水平
将蛋白质表达量按不同 水平分组，并通过直方 图呈现各组频数，有助 于分析蛋白质功能与疾 病的关系。
代谢物浓度分布
利用频率分布直方图展 示生物样本中代谢物的 浓度分布情况，为代谢 组学研究和疾病诊断提 供参考。
THANKS
感谢观看
处理异常值
在绘制频率分布直方图之前，可以对数据进行预处理，例如采用箱线图等方法识别并处理 异常值，以减少异常值对直方图形状的影响。同时，也可以在直方图上标注出异常值的位 置和数值，以便观察者更好地了解数据的分布情况。
06
案例：频率分布直方图在医学领域应
用
疾病发病率分布情况展示
发病率地域分布
通过频率分布直方图展示不同地区的疾病发病率，帮助医学研究 者识别高发区域和潜在风险因素。
图形表示不同
条形图用条形的长度表示各类别数 据的频数或频率，而频率分布直方 图用矩形的面积表示各组数据的频 数或频率。
横轴意义不同
条形图的横轴表示类别，而频率分 布直方图的横轴表示数据范围。
02
绘制频率分布直方图步骤
数据收集与整理
收集数据
根据研究目的确定需要收集的数据，并确保数据的准确性和 完整性。
频率分布直方图
汇报人：XX
• 频率分布直方图基本概念 • 绘制频率分布直方图步骤 • 频率分布直方图解读技巧 • 频率分布直方图在数据分析中应用 • 频率分布直方图优缺点及改进措施 • 案例：频率分布直方图在医学领域应

点击确定171726264正态分布2在函数对话框中x输入f15mean输入b18standarddev输入b19cumulative输入0在函数栏中在b18b19的中间添加符号b18b19点击确定181826264正态分布3向下填充之后下拉单元格即可191926265正态分布曲线图1在直方图中增加正态分布曲线图4确定确定202026265正态分布曲线图21212626101520253035频率正态分布曲线5正态分布曲线图2调整图形1在图表区柱形较下方选中正态分布曲线数据正态分布密度值和频率数值相比太小了实在看不清多试几次选中后如图同时正态分布曲线那数数据处于选中状态
5/ 26
2、分组
1、根据之前得出结论，总共分成8组，第一组 上组界值是7.95，组距是0.5，所以第二组是 7.95+0.5=8.45，以此类推。直到之后一组的 下组距大于11.9
6/ 26
2、统计频率
• “频率”就是去统计每个分组中所包含的数据的个数。 • 最简单的方法就是直接在所有的数据中直接去统计，但当数 据量很大的时候，这种方法不但费时，而且容易出错。 • 这里介绍的是“FREQUENCY（频率分布）”函数方法和EXCEL 数据分析法：统计每个小组的数据个数 “Date_array 数据区域”：是选取要统计的数据源，就是选 择原始数据的范围； “Bins_array 分段点（区间）”：是选取直方图分组的数据
20 频率 15 正态分布曲线
10
5
0 1 2 3 4 5 6 7 8 9
22/ 26
5、正态分布曲线图
2、调整图形 1、在图表区柱形较下方选中正态分布曲线数据，（正态分布密度值和频率数值 相比太小了，实在看不清，多试几次，选中后如图，同时正态分布曲线那数 数据处于选中状态）。

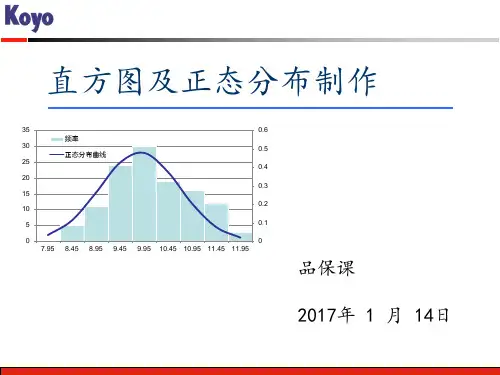
直方图和正态分布图
直方图（Historgram）是将某期间所收集的计量值数据经分组整理成次数统计表，并使用柱形予以图形化，以掌握这些数据的分布状况。

直方图的应用
制造---加工尺寸的分布
经济---收入支出的分布
教育---考试成绩的分布……
●直方图是反映分组数据频数的柱形图
●正态分布图是一条单峰、对称成钟形的曲线。

Frequency函数
●以一个垂直数组返回某个区域中数据的频率分布
●由于函数frequency返回返回一个数组，所以必须以数组公式的形式输入
Frequency（data_array，bins_array）:
data_array为一数组或对一组数值的引用，用来计算频率。

Bins_array 为间隔的数组或对间隔的引用，该间隔用于对data_array中的数值进行分组
Normdist函数
返回指定平均值和标准偏差的正态分布函数
Normdist (x，mean，standard_dev，cumulative)
其中x为需要计算其分布的数值
Mean 分布的算术平均数
Standard_dev 分布的标准偏差
Cumulative 如果为false，则返回概率密度函数
正态分布图的差异：中心偏移，分布不同
分析工具库-安装加载宏：制作直方图
VBA：全称Visual Basic for Application, 它是Visual Basic 的应用程序版本，是面向对象的编程语言。

VBA也可应用于AutoCAD
VBA的应用
●自动执行重复的操作
●进行“智能化”处理
●Office二次开发的平台。

(14)曲(3线) (的4)对称位置由μ确定，曲线的形状由σ确定，σ越大，曲线越“矮胖”，反之，曲线越“瘦高”.
布 N (0，1) ， 已 知 p （ ＜ － 1.96 ） =0.025 ， 则 即2、考已试知成X绩~N在((08,10),1，00则)间X在的区概间率为0. 内取值的概率等于（ ）
(2)曲线对应的正态总体概率密度函数是偶函数；
(3)曲线在x＝ 处处于最高点，由这一点向左右两侧延
伸时，曲线逐渐降低；
(4)曲线的对称位置由μ确定，曲线的形状由σ确定， σ越大，曲线越“矮胖”，反之，曲线越“瘦高”.
上述叙述中，正确的有 (1) (3) (4) .
课堂练习
1. 右图是当 σ 分别取值 σ1，σ2，σ3 的三种正
(2)
1 , 2 1 (x1)2
(x) 新疆 王新敞 奎屯
e 8 ,x ( , )
22
说明：当0 , 1时，X 服从标准正态分布
记为X~N (0 , 1)
例2、下列函数是正态密度函数的是（ B ）
f(x) 1 e ,,(0)都 是 实 数 A. 说明：当m=0 , s =1时，X 服从标准正态分布 2 样本容量增大时频率分布直方图
随 着 重 复 次 数 ,这的个增频加率 直 方 图 的
会 越 来 越 像 一线 条图钟 2.4形 3曲 .
y
O
图2.43
x
这条曲线 (或就 近是 似 )下地 列函数:的图象
φμ,σx 1 ex 2 σ μ 22,x , ,
2π σ
其 中 μ 和 σ σ 实 0 为 数 .我 参φ 们 μ 数 ,σ x 的 称
1 即即(947)考考7曲2试 试线成成的D.绩绩对在在称((位8800置,,1100由00))μ间间确的的定概概，率率曲为为线00的.. 形状由σ确定，σ越(x大4，1)曲2线越“矮胖”，反之，曲线越“瘦高”.

正态分布直方图是一个常见的统计图形，它可以帮助我们更好的了解
一组数据的分布。

正态分布图表可以帮助科学家了解数据的分布情况，更好的进行研究。

正态分布直方图利用数据的频率分布，将一组数据在横坐标上按照数
值大小进行分类，在纵坐标上表示同一分类所含数据量。

可以从正态
分布图上看出，数据是如何分布的。

正态分布图可以帮助我们测算数据的中心位置和离散程度，帮助我们
分析数据间的关系和变化。

正态分布图也可以当做风险分析和投资分
析时重要的参考。

正态分布直方图是统计学家们最重要，最常用也是最有价值的工具。

它对科学家们分析数据和做决策的时候都会起到重要的作用，是非常
值得重视的。

总之，正态分布直方图是统计学中最重要的工具之一，可以分析数据
的分布情况，帮助我们更好的进行研究总结，是非常实用的工具。

例3： 正态总体为 ： 正态总体为µ=0， ， x2 1 −2 σ=1时的概率密度函数是 f ( x) = 2π e , x∈R 时的概率密度函数是 (1)求证：f(x)是偶函数； 求证： 是偶函数 是偶函数； 求证 (2)求f(x)的最大值； 求 的最大值； 的最大值 (3)利用指数函数的性质说明 的增减性． 利用指数函数的性质说明f(x)的增减性 利用指数函数的性质说明 的增减性．
1 2 π
5 10 15 20 25 30 35 x
练习3: 练习
已知函数f ( x ) =
1
2p X轴上方 轴上方 a、它的图象在__________
1
e
x2 2
，则
b、它的最大值是________ 2p 直线x=0 直线x=0 ________对 c、它的图象关于________对称
在实际遇到的许多随机现象都服从或近似服 从正态分布： 从正态分布：
以及降雨量等，水文中的水位； 以及降雨量等，水文中的水位；
总之，正态分布广泛存在于自然界、 总之，正态分布广泛存在于自然界、生 产及科学技术的许多领域中。 产及科学技术的许多领域中。 正态分布在概率和统计中占有重要地位。 正态分布在概率和统计中占有重要地位。
4、正态曲线的性质 、
①曲线在坐标平面的什么位置？ 曲线在坐标平面的什么位置？ 曲线的变化趋势如何？ ③ 曲线的变化趋势如何？
一般正态分布为一个分布族:N(µ,σ2) ；标准 µσ 正态分布只有一个 N(0,1) ；这样简化了应
用
正态曲线下的面积规律
• X轴与正态曲线所夹面积恒等于 。 轴与正态曲线所夹面积恒等于1 轴与正态曲线所夹面积恒等于 • 对称区域面积相等。 对称区域面积相等。
S(-∞,-X)

A、与双峰型类似，多个总体、多总分布混在一起。 B、由于生产过程中某中缓慢的倾向在起作用， 如工具的磨损、操作者的疲劳等。 C、质量指标在某个区间中均匀变化。
1.4 直方图应用
当直方图的形状呈正常型时，即工序在此时刻处于稳定状态时，还需要进 一步讲直方图同规格界限（即公差）进行比较，以分析判断工序满足公差 要求的程度。
制限位于μ±3σ处，另外两条线位于μ±σ处。
若总体均数和标准差未知，可用 x 和s 来估计，此时，7条水平线分别 为： x ，x ±s , x ±2s , x ±3s 。
2.6.2 控制图
4.质量控制图的做法 对某一观察指标，依时间顺序记录其观察数据，并在控制图上依次
描出各点。若出现以下8种情况之一，则有理由认为其数据波动不 仅仅是随机测量误差所引起，而是可能存在某种系统误差。
利用此原理，人们可进行测量过程的质量控制。
2.6.2 控制图
2. 质量控制的工具 质量控制主要通过控制图来实现。控制图的基本原理是：若某一变动仅仅由
个体变异或随机误差所致，则该指标的观察结果服从正态分布。 3. 质量控制图的构成 控制图有7条水平线：中心线位于总体均数μ处，警戒限位于μ±2σ处，控
3、80%的销售额由20%的产品带来；
4、用于发现现场的重要问题点。 4、80%的品质成本由20%的品质问题造
5、用于整理报表或记录。
成；
6、可作不同条件的评价。
5、80%的品质问题由20%的人员引起
谢谢
85.1%
81.6%
0.8
76.3%
80
0.7
63.2% 0.6
60 45.6%
40
0.5 次数
0.4 累计比例
0.3

频数分布图一（又称直方图）
30
20
从频数表及频数分布图上可得 知： 该数值变量资料频数分 布呈现中间频数多，左右两侧 基本对称的分布。所以我们通 俗地认为该资料服从正态分布。
频数
10 0 130.5 133.5 136.5 139.5 142.5 145.5 148.5 151.5
154.5
157.5
正态分布
正态分布的概念

正态分布的通俗概念： 如果把数值变量资料编 制频数表后绘制频数分布图（又称直方图，它用 矩形面积表示数值变量资料的频数分布，每条直 条的宽表示组距，直条的面积表示频数（或频率） 大小，直条与直条之间不留空隙。），若频数分 布呈现中间为最多，左右两侧基本对称，越靠近 中间频数越多，离中间越远，频数越少，形成一 个中间频数多，两侧频数逐渐减少且基本对称的 分布，那我们一般认为该数值变量服从或近似服 从数学上的正态分布。
其基本步骤如下： 已知 X～N（μ ，σ ） ， 求随机变量 X 出现在 区间（x1,x2）的概率 即求 服从 一般 正态 分 布 N（μ ，σ ）的随机 变量 X 在区间（x1,x2） 所对应的面积
2 2
进行标准化变换：
U
x

求服从标准正态分布 N （０，１）的随机变量
U 在区间（u1,u2）所对
侧的面积为α /2, 从- U
2
到-∞这
一侧的面积也为 α /2,两侧面积之 和为α 。 即在随机 变量 U 的所有取 值中，有 100α 的 值比 U 大， 有
100（1-α ）的值 比 U 小。
正态分布曲线及其面积分布： 在正态曲线下，μ ±1σ 、μ ±1.96σ 和μ ±2.58σ 所对应的面积分别为 0.6827、0.9500 和 0.9900。 图一：

用Excel做直方图（2）：频率分布直方图一、什么是直方图1、定义直方图是一种条形图，是以组距为底边、以频数为高度的一系列连接起来的直方型矩形图2、相关概念组数：在统计数据时，把数据按照不同的范围分成几个组，分成的组的个数称为组数。

组距：每一组两个端点的差规格上限：Tu规格下限：Tl公差中心：M=3、步骤1. 求出其最大值和最小值。

2. 将数据分成若干组，并做好记号。

3. 计算组距的宽度。

用最大值和最小值之差（极差）去除组数，求出组距的宽度。

4. 计算各组的界限位。

各组的界限位可以从第一组开始依次计算，第一组的下界为最小值减去最小测定单位的一半，第一组的上界为其下界值加上组距。

第二组的下界限位为第一组的上界限值，第二组的下界限值加上组距，就是第二组的上界限位，依此类推。

5. 统计各组数据出现频数，作频数分布表。

6. 作直方图。

以组距为底长，以频数为高，作各组的矩形图。

4、注意事项：1. 数据量在50个以上2. 分组数在5~12个为宜3. 在直方图上应标注出公差范围(T)、样本容量(n)、样本平均值(x)、样本标准偏差值(s)和x的位置二、实战：用Excel做直方图1、获取数据源按照上节内容讲的随机数发生器，我们随机生成均值为0，标准差为1的100个符合正态分布的数据，用这100个数据来做频率分布直方图。

生成的数据如A列所示。

2、计算相应值我们要算出这组数据的个数，最大值、最小值、平均值、极差（最大值-最小值）、组数和组距。

相应的公式如下图所示。

组数：其中组数是这组数组被分成组的个数，是对数据个数开方然后向上取整求出。

组距：组距是每一组数两个端点的差，用极差除以组数求得。

这里提供另外一种直接生成数据描述性统计分析的值的方法，Excel——数据分析工具库——描述统计分析工具，直接生成关于一组数据的“描述统计”分析工具用于生成数据源区域中数据的单变量统计分析报表，组数和组距还是要手动公式输入，这里的描述性统计分析只是用来提供有关数据趋中性和易变性的信息。

如下表：
区 间 取值概率 68.26% 95.44% 99.74% （μ －σ ，μ ＋σ ] （μ －2 σ ，μ ＋2 σ ] （μ －3 σ ，μ ＋3 σ ]
上述结果还可用下图表示：
68.26% 95.44% 99.74%
可以看到，正态总体几乎总取值于区间 3 , 3 之内.而在此区间以外取值的概 率只有0.0026，通常认为这种情况在一次试验中 几乎不可能发生(小概率事件). 在实际应用中，通常认为服从于正态分布 N(μ,σ2)的随机变量X只取 3 , 3 之间的 值，并简称之为3σ原则.
选修2-3
2.4 正态分布
情境引入
1. 高 尔 顿 钉 板 实 验
2.高尔顿板试验过程
重复进行高尔顿板试验， 随着试验次数的增加， 掉入各个球槽内的小球 的个数就会越来越多， 堆积的高度也会越来越 高.各个球槽内的堆积高 度反映了小球掉入各球 槽的个数多少.
高尔顿板示意图
3. 频率分布直方图
为了更好地考察随着试验次数的增加，落在各个球 槽内的小球分布情况，我们进一步从频率的角度探究一 下小球的分布规律. 以小球的编号为
O
a
b
x
3. 正态曲线的特点
y
μ= -1 σ=0.5 μ=0 σ=1
y
y
μ=1
σ=2
-3 -2 -1 0
1 2
x
-3 -2 -1 0
1 2
3
x
-3 -2 -1 0
1
2 3
4x
具有两头低、中间高、左右对称的基本特征
3. 正态曲线的特点
(1)曲线在x轴上方，与x轴不相交； (2)曲线是单峰的，它关于直线x=μ对称； (3)曲线在x=μ处达到峰值(最高点) (4)曲线与x轴之间的面积为1.

区间（-∞，a）， P( a) 的值为下图中阴影部分的面积．
动 脑 思 考 探 索 新 知
设随机变量 ~ N (0，． 1) 由概率密度曲线的定义知道，任给
区间（-∞，a）， P( a) 的值为下图中阴影部分的面积．
P(a b) 的值为下图中阴影部分的面积．因此，
动 脑 思 考 探 索 新 知
创 设 情 境 兴 趣 导 入
［145.5，148.5）
［148.5，151.5）
［151.5，154.5）
3 一 正￣
6 8 18 11 10
0.050
0.100 0.133 0.300 0.183 0.167
［154.5，157.5） 正 ［157.5，160.5） 正正正 一 ［160.5，163.5） 正正￣ ［163.5，166.5） 正正
（2）该厂某一周加工该零件5000个，求直径在41～43 mm之间的
巩 固 知 识 典 型 例 题
零件的大约个数．
解
故 （1）因为 40， 2，
P(41 ≤ ≤ 43) ( 43 40 41 40 ) ( ) 2 2 (1.5) (0.5) 0.2417．
1) 0, 1 的正态分布叫做标准正态分布，即 ~ N (0，．
标准正态分布的密度函数为
动 脑 思 考 探 索 新 知
f ( x)
1 2π
e

x2 2
,( x )
相应的曲线叫做标准正态分布曲线（如图）．
设随机变量 ~ N (0，． 1) 由概率密度曲线的定义知道，任给
时，曲线逐渐降低，呈现"中间高，两边低"的形状；
动 脑 思 考 探 索 新 知

[一点通]
解决此类问题一定要灵活把握3σ原则，将
所求概率向P(μ－σ<X<μ＋σ)，P(μ－2σ<X<μ＋2σ)，P(μ－
3σ<X<μ＋3σ)进行转化，然后利用特定值求出相应的概 率．同时要充分利用好曲线的对称性和曲线与x轴之间的面 积为1这一特殊性质．
6．某人从某城市的南郊乘公交车前往北区火车站，由于 交通拥挤，所需时间(单位：分)服从X～N(50,102)， 则他在时间段(30,70)内赶到火车站的概率为______． 解析：∵X～N(50,102)，∴μ＝50，σ＝10.
3．正态分布的 3 原则
(1) P( X ) 68.3% (2) P( 2 X 2 ) 95.4%
(3) P( 3 X 3 ) 99.7%
正态变量的取值几乎都在距x＝μ三倍标准差之内，这就 是正态分布的3σ原则．
复习
100个产品尺寸的频率分布直方图
频率 组距
产品 尺寸 （mm)
25.235 25.295 25.355 25.415 25.475 25.535
复习
200个产品尺寸的频率分布直方图
频率 组距
产品 尺寸 （mm) 25.235 25.295 25.355 25.415 25.475 25.535
复习
频率 组距
样本容量增大时 频率分布直方图
分布密度曲线
产品 尺寸 (mm)
这条曲线称为随机变量X的分布密度曲线，此曲线对应的函 数称为X的分布密度函数，记为f(x).
频率 组距
产品尺寸X的 分布密度曲线
产品 尺寸 (mm)
频率 组距
产品 尺寸 (mm) a b

7
正态分布的概率密度

正态曲线（normal curve）：高峰位于中 央，两侧逐渐下降并完全对称，曲线两 段永远不与横轴相交的钟型曲线。
正态曲线的函数表达式 f ( x) 称为正态分布 概率密度函数：
1 f ( x) e 2 ( x )2 2 2

8
正态分布的参数

如果变量X的概率密度函数服从上述函数，则称
4
概率密度

组段
各个组段的概率
95100105110115120125130135140-
概率 0.0006 0.0049 0.0440 0.1532 0.2936 0.3037 0.1515 0.0421 0.0061 0.0003
– P(110cm身高<115cm)= 0.153 – P(105cm身高<120cm)= 0.0440+0.1532+0.2936=0.4908 – P(身高<120cm)= 0.4963 组距越小，组段就越多，能够计算概率的区 间就越多
肺通气量的95%参考值范围 – 根据肺通气量的背景和已知的影响因素，制定 入选标准和排除标 – 入选标准和排除标准所确定的人群中随机抽样 – 确定单双侧和分布：单侧，近似正态 – 已知 x =4.5L, s=0.6L.
22
参考值范围估计正态分布法 分位数法双侧%
单侧
只有下 限 只有上 限
双侧
单侧
16
标准正态分布曲线下面积 (u) 表、图
17
-1.96≤x≤1.96的概率：
18

例：设u1=-1.83,u2=-0.3，求标准正态分布曲
线下（-1.83，-0.30）范围内的面积