影响加速度的因素31页PPT
- 格式:ppt
- 大小:2.44 MB
- 文档页数:31
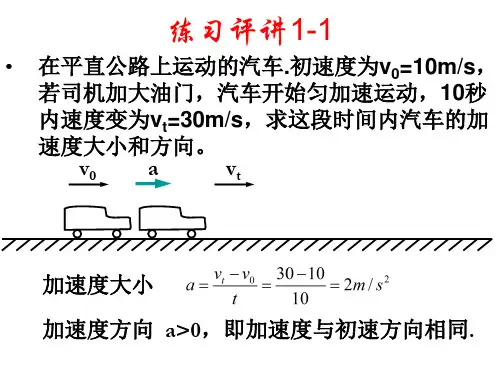



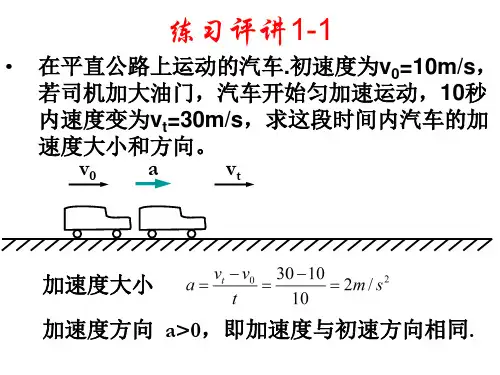
影响加速度的因素合作与讨论如果你坐在一辆以恒定的牵引力正在加速启动的卡车上,突然车上一个很重的货物从车尾掉下来,如果不考虑司机听到声音和从观后镜看到货物,你能否知道货物已掉了?我的思路:开始时物体的加速度情况,货物掉下车之后,车的加速度怎样变,这个变化体现为车的运动怎样变化? 思路分析1.本节主要是实验方法、原理的教学,并通过学生定性的实验探究为下一节的定量研究作好准备. 2.首先要引导学生就影响加速度的因素大胆猜测、提出假设,并允许学生一边交流讨论,一边进行实验.使学生对影响加速度的因素有一个直观的认识.3.鼓励学生就自己的假设提出实验方案.条件允许时,挑选优秀方案交流.一定要让学生获得成功的快乐.4.让学生亲自作好实验,通过实验直接体会哪些因素影响加速度是本节的突破口. 相关链接实验计算加速度的两种方法的优劣分析实验计算加速度都认为逐差法好,本文的目的:从公式推导上揭示逐差法积累误差大,再从实际的误差原因分析,得出其平均值偏离真实值较大;用以往称赞逐差法的理由去否定逐差法,从而得出正确的比较优越的计算方法. 一、公式推导物体做初速度为v 0,加速度为a 的匀变速直线运动,由位移公式和速度公式,可推得: s 1=v 0t +221at ,v 1=v 0+at 所以△s =s 2-s 1=aT 2由逐差法得出 s 4-s 1=(s 4-s 3)+(s 3-s 2)+(s 2-s 1)=3aT2所以由逐差法得出a 1=2143Ts s -,a 2=2253T s s -,a 3=2363T s s - 所以a =3321a a a ++=21234569)()(T s s s s s s ++-++ (1)逐差法又认为:利用△s =aT 2计算a ,则a 1=212Ts s -,a 2=223T s s -,a 3=234T s s -,a 4=245T s s -,a =256T s s - a =554321a a a a a ++++=256453423125T s s s s s s s s s s -+-+-+-+-=2165T s s - (2)所以,逐差法认为(1)式利用了s 1~s 6六个数据,而②式只利用了s 6和s 1两个数据,失去了多个数据,互相抵消,失去消除测量的偶然误差的作用,(1)式误差较小.对于理想的情况下,(1)、(2)两式并无多大差别.对于打点时产生的阻力,则打点越多而积累的迟滞影响越大.设打点时产生的平均阻力为f ,打点时与纸带的接触时间为t ,则每打一次点,产生的速度减小量为△v ,f ·t =m ·△v .显然(1)式比(2)式复杂些.再将以上两式进行推导分析得到:由(1)得a 1=2143Ts s -=21223343T s s s s s s -+-+-=21233T s s s ∆∆∆++ 同理a 2=22343T s s s ∆∆∆++,a 3=23453T s s s ∆∆∆++ 所以a =2543219222T s s s s s ∆∆∆∆∆++++ ①由(2)得a 1=212T s s -=21T s ∆,a 2=223T s s -=22T s ∆ a 3=234T s s -=23T s ∆,a 4=245T s s -=24T s∆,a 5=256T s s -=25T s ∆a =2543215Ts s s s s ++++∆∆∆∆ ② 比较①和②两式,看到两式的本质形式仍是a =2Ts ∆由①得s ∆=91(△s 1+2△s 2+2△s 3+2△s 4+△s 5) ③ 而由②得s ∆=51(△s 1+△s 2+△s 3+△s 4+△s 5) ④ 显然,由④式得的平均位移差是偏重于中间段,按误差理论△s 3和△s 1、△s 5加权为3,△s 2和△s 4加权为2,误差的积累作用已可说从公式推导中揭示出来.从打点形成的迟滞影响,越到后面实验的各计时点的瞬时速度与理想值减小越多,要加权也没有任何理论在中间段加权3次.所以①式揭示了逐差法积累因素大,是人为采取方法不当造成的,属偶然误差范畴.而由④式则揭示了5段△s 是机会均等的,与①式比较则较合理些. 二、实际情况分析教材对(2)、②式采用1a =212Ts s -,没有类似于逐差法的命名,这里不妨给予简称为邻差法.邻差法采用公式是a =212Ts s -,下面分析该式的实际情况.对于s 1=v 0t +221at ,s 2=v 1t +221at 而言,s 2-s 1=(v 1-v 0)T ,v 1和v 0为最接近的两个计数点“0、1”的瞬时速度,实验速度比理想的真实速度小n .△v 值(设“0”点之前打了n 次点),v 1的实验速度比理想的真实速度小(n +5)△v 的值,与打点时间、运动时间都相同,速度值又最贴近,双方都由于打点迟滞影响了一些位移,所以实验差值s 2-s 1=(v 1-v 0)T 只比理想的真实值小5·△v ·T ,这是实验的系统误差.按上述分析可见a 2=223T s s -……a 5=256T s s -,各 段△s 差值都比相应的理想真实值小5·△v ·T .考虑实验时一些偶然误差,必然△s 1≈△s 2≈△s 3≈△s 4≈△s 5,△s =(v 1-v 0)T ,恰好消除了“0”点之前的迟滞影响,用③式计算是合理的.对于(1)式而言,a 1=2143Ts s -,由于打点的迟滞影响,s 4段位移值必然比理想的值s 4差距较大,而原式是由理想情况推导出来的(不计打点的阻力),所以(1)式推导出a =2143T ss -,没有a =2132Ts s -误差小.同样可推出a =212Tss -,由于积累和误差降到不可再降的最小限度,且消除了以前打点产生的积累误差.可见,实际情况分析也是(2)式比(1)式优越一些.三、用逐差法原有赞词去否定逐差法不论逐差法、还是邻差法,给定一条纸带求其运动加速度.必须先设定计数点,验证相邻段相等时间内位移之差是否近似相等(在误差范围内),这样在前提保证下才可用(1)式或(2)式计算a值.只有逐差法将6段s值都用到.逐差法原有赞词认为它可消除偶然误差,则邻差法式(2)如果s6,s1发生偏差则后果不堪设想.而邻差法(2)式正因为有上述前提作保证,且计数点是任取的(可以往前或往后一些选取第一点“0”,是随机的不可能有偏差太大,如果真的太大则前提△s不近似相等在误差范围内),也不能求a值;反之,根据①式推导,也可用同样理由反击逐差法,如果△s3=s4-s3,s4和s3误差太大,则△s3加权3,则误差必然更大了.而(2)式a=216 5T ss-,也正是在消除前后的积累误差,且在保证大前提基础上得到的简化公式.所以如果采用邻差法(2)式计算,则在大前提保证之下,不仅从理论上、实际情况下分析都具有比逐差法误差小的优点,且计算公式也简捷准确.知识总结1.在物理学中,研究三个物理量的关系时,要采取控制变量的方法来研究,即先确定一个量,然后去分析另外两个物理量的关系.这种方法在物理学的研究中有重要的应用,在学习中要注意体会.2.质量一定时,合外力大,物体的加速度大,合外力小,物体的加速度小;在合外力一定时,质量大,物体的加速度小,质量小物体的加速度大.3.讨论加速度变化时,一定要清楚有两个因素——质量和合外力会影响加速度的大小,所以,必须要采用控制变量的方法来讨论加速度的变化.2019-2020学年高考物理模拟试卷一、单项选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的1.科学家对物理学的发展做出了巨大贡献,也创造出了许多物理学方法,如理想实验法、控制变量法、极限思想法、建立物理模型法、类比法和科学假设法等,以下关于物理学史和所用物理学方法叙述正确的是()A.卡文迪许巧妙地运用扭秤实验测出引力常量,采用了理想实验法B.牛顿通过比较月球公转的向心加速度和地球赤道上物体随地球自转的向心加速度,对万有引力定律进行了“月一地检验”,证实了万有引力定律的正确性C.在不需要考虑物体本身的形状和大小时,用质点来代替物体的方法叫假设法D.在推导匀变速直线运动位移公式时,把整个运动过程分成很多小段,每一小段近似看作匀速直线运动,然后用各小段的位移之和代表物体的位移,这里采用了微元法2.如图所示,有10块完全相同的长方体木板叠放在一起,每块木板的质量为100g,用手掌在这叠木板的两侧同时施加大小为F的水平压力,使木板悬空水平静止。