几种特殊矩阵的生成

MATLAB单元矩阵在MATLAB中，单元矩阵是一种特殊的矩阵，其中所有对角线上的元素都为1，而其余元素都为0。

它在数值计算和图像处理等领域中有广泛的应用。

本文将介绍单元矩阵的定义、性质、生成方法以及在MATLAB中的应用。

定义和性质单元矩阵（Unit Matrix），又称为单位矩阵或恒等矩阵，是一个n阶方阵，其中所有对角线上的元素都为1，而其余元素都为0。

以符号表示为I或者E(n)，其中I表示Identity Matrix（单位矩阵），E(n)表示n维单位矩阵。

单元矩阵具有以下几个重要性质：1.单位性质：任何一个与单元矩阵相乘的方阵结果都是其本身，即 A * I = I* A = A。

2.封闭性质：两个单元矩阵相加或相乘仍然得到一个单元矩阵。

3.幂运算：单元矩阵的幂运算结果仍然是它本身。

生成方法在MATLAB中，可以使用以下几种方法生成一个单元矩阵：方法一：使用eye函数MATLAB中的eye函数可以生成一个指定大小的单元矩阵。

语法格式为：I = eye(n)其中，n表示生成的单元矩阵的大小。

方法二：使用ones和diag函数MATLAB中的ones函数可以生成一个全为1的矩阵，而diag函数可以将一个向量的元素设置为对角线上的值。

通过结合这两个函数，可以生成一个单元矩阵。

语法格式为：I = diag(ones(n, 1))其中，n表示生成的单元矩阵的大小。

方法三：使用spdiags函数MATLAB中的spdiags函数可以在指定位置生成一个带有指定值的对角线矩阵。

通过设置对角线位置和对应值，可以生成一个单元矩阵。

语法格式为：I = spdiags(ones(n, 1), 0, n, n)其中，n表示生成的单元矩阵的大小。

MATLAB中的应用在MATLAB中，单元矩阵常用于以下几个方面：线性代数运算在线性代数运算中，单元矩阵常作为单位元素参与计算。

例如，在求解线性方程组时，常常需要用到逆矩阵来消去系数矩阵，并且逆矩阵与系数矩阵相乘的结果应为单元矩阵。

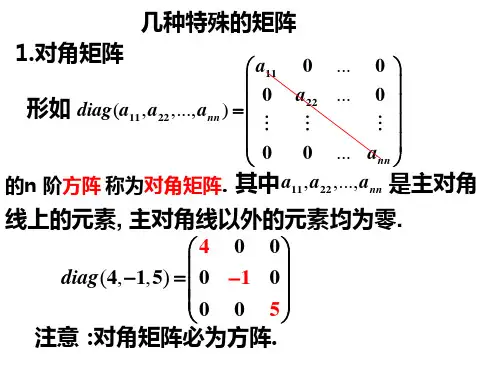
三对角矩阵在中，一个三对角矩阵是的一种，它“几乎”是一个。

准确来讲：一个三对角矩阵的在上，或比主对角线低一行的对角线上，或比主对角线高一行的对角线上。

例如，下面的是三对角矩阵：性质三对角矩阵是。

尽管一样的三对角矩阵不必然是或，许多解线性代数问题时显现的矩阵却往往有这些性质。

进一步若是一个实三对角矩阵A 知足a k,k+1 a k+1,k > 0，因此它元素的符号都为正，从而于一个埃尔米特矩阵，如此都是实数。

后一个推论若是咱们将条件a k,k+1 a k+1,k > 0 换为a k,k+1 a k+1,k≥0，结论仍然成立。

所有n×n三对角矩阵的组成一个3n-2维。

许多线性代数应用于对角矩阵时所需专门少，这种改良也常常被三对角矩阵继承。

譬如，一个n 阶三对角矩阵A的能用（）的公式计算：那个地址是第k个主，即是由A最开始的k行k列组成的子矩阵。

用此方式计算三对角矩阵所需计算量是线性n，但是关于一样的矩阵复杂度是n 的3 次方。

计算程序一个将一样矩阵变成海森堡型的变换，将厄密特矩阵变成三对角矩阵。

从而，许多运用到厄密特矩阵上，第一步将输入的厄密特矩阵变成三对角矩阵。

一个三对角矩阵利用特定的比一样矩阵所用的存储空间也少得多。

例如，包将一个n-维非对称三对角矩阵存为三个1-维数列，其中一个长n包括对角元素，其它两个长为n−1 包括下对角线和上对角线元素。

三对角矩阵方程，能用一种需要O(n)次操作的解出来（Golub and Van Loan）。

正交矩阵概述正交矩阵是实数特殊化的，因此老是。

尽管咱们在那个地址只考虑实数矩阵，那个概念可用于其元素来自任何的矩阵。

正交矩阵毕竟是从内积自然引出的，关于复数的矩阵这致使了归一要求。

要看出与内积的联系，考虑在n维实数中的关于正交基写出的向量v。

v的长度的平方是v T v。

若是矩阵形式为Q v的线性变换维持了向量长度，那么。

因此有限维线性，比如、和它们的组合，都产生正交矩阵。

特殊矩阵总结
常用的产生通用特殊矩阵的函数有：
zeros:产生全0矩阵（零矩阵）
ones:产生全1矩阵（幺矩阵）
eye：产生单位矩阵
rand:产生0~1间均匀分布的随机矩阵
randn:产生均值为0，方差为1的标准正态分布随机矩阵
zeros(m):产生m*m零矩阵
zeros(m,n):产生m*n零矩阵。

当m=n时，等同于zeros(m)
zeros(size(A))：产生与矩阵A同样大小的零矩阵
魔方矩阵：其每行、每列及两条对角线上的元素之和都相等。

函数为magic（n），功能是生成一个n阶魔方矩阵。

范德蒙德矩阵：其最后一列全为1，倒数第二列为一个指定的向量，其他各列是其后列与倒数第二列的点乘积。

函数为vander(V)
希尔伯特矩阵：矩阵的每个元素hij=1/(i+j-1)。

函数为hilb（n），逆函数为invhilb（n）
format rat以有理数形式输出
特普利茨矩阵：第一行和第一列外，其他每个元素都与左上角的元素相同。

生成特普茨矩阵的函数是toeplitz(x,y),它生成一个以x为第一列，y为第一行的托普利兹矩阵，x和y不必等长。

伴随矩阵：compan（p）高次幂系数排在前，低次幂排在后。

帕斯卡矩阵：pascal（n）。

三对角矩阵在线性代数中，一个三对角矩阵是矩阵的一种，它“几乎”是一个对角矩阵。

准确来说：一个三对角矩阵的非零系数在主对角线上，或比主对角线低一行的对角线上，或比主对角线高一行的对角线上。

例如，下面的是三对角矩阵：性质三对角矩阵是海森堡矩阵。

尽管一般的三对角矩阵不一定是对称或埃尔米特矩阵，许多解线性代数问题时出现的矩阵却往往有这些性质。

进一步如果一个实三对角矩阵 A 满足a k,k+1 a k+1,k > 0，所以它元素的符号都为正，从而相似于一个埃尔米特矩阵，这样特征值都是实数。

后一个推论如果我们将条件a k,k+1 a k+1,k > 0 换为a k,k+1 a k+1,k≥ 0，结论仍然成立。

所有n×n三对角矩阵的集合组成一个3n-2维向量空间。

许多线性代数算法应用于对角矩阵时所需计算量特别少，这种改进也经常被三对角矩阵继承。

譬如，一个 n 阶三对角矩阵A的行列式能用continuant（Continuant）的递归公式计算：这里是第k个主子式，即是由A最开始的k行k列组成的子矩阵。

用此方法计算三对角矩阵所需计算量是线性n，然而对于一般的矩阵复杂度是 n 的 3 次方。

计算程序一个将一般矩阵变成海森堡型的变换，将厄密特矩阵变成三对角矩阵。

从而，许多特征值算法运用到厄密特矩阵上，第一步将输入的厄密特矩阵变成三对角矩阵。

一个三对角矩阵利用特定的存储方案比一般矩阵所用的存储空间也少得多。

例如，LAPACK Fortran包将一个n-维非对称三对角矩阵存为三个 1-维数列，其中一个长n包含对角元素，其它两个长为n− 1 包含下对角线和上对角线元素。

三对角矩阵方程，能用一种需要O(n)次操作的特殊的算法解出来（Golub and Van Loan）。

正交矩阵概述正交矩阵是实数特殊化的酉矩阵，因此总是正规矩阵。

尽管我们在这里只考虑实数矩阵，这个定义可用于其元素来自任何域的矩阵。

正交矩阵毕竟是从内积自然引出的，对于复数的矩阵这导致了归一要求。

偷得半日清闲，来写这个前几天承诺好的东西，如果不出意外，以后每周六就写这么一篇出来，周期不会短也不会太长，毕竟我也在慢慢的学东西，只能从基础的一点点写起，也算给自己的一个复习的机会了，我打算在后面先写一点控制理论的东西，然后用小麦做出来或举些其他的例子，然后留下一些简单问题让大家去做，再然后在下篇里给出解决的方法，很多问题和观点都是基于我个人对控制系统理论与MATLAB的理解，错误和不周是难免的，希望大家多多指正，一些好的，更有效率的实现方法也希望大家能提出来，我们共同提高，讲述风格么，还是轻松和口语化一些，一些术语当然是必须的，但我会尽量说的明白一些，目的让大家能迅速的熟悉小麦以及如何把他应用到我们控制系统的分析设计中去，闲话不多说了，现在开始吧！要从哪里开始呢，我觉得一上来就讲控制理论和小麦有点那个……还是先说一些关于小麦本身比较基本的东西和一些必须要注意的问题，目的是让那些刚刚接触小麦的朋友不至于对我们可爱的小麦产生恐惧，小麦对于学控制的人来讲，就像是手里笔和草纸，它可以帮助你完成一些复杂的计算，可以帮你作图，分析，但请记住，说到底，这个东西就是一个工具，它不能代替你思考，学它的目的是为了更好的研究我们学习的领域，因此不要为学软件而学软件，既然是工具，就必须学以至用。

小麦的最大好处是，编写程序简单得要死，在写算法的时候只需要按我们平常的书写公式的习惯和思考逻辑来写就可以了，而用其他语言，受到语法规则等的限制，对编程不熟悉的人估计会很快疯掉。

关于小麦的历史什么就不说了，强烈建议大家使用用比较新版本的小麦（现在最新的好像是r2007b），这样会给你处理问题带来方便（后面我会举例说明这个问题）。

当你打开小麦界面的时候，会看到有几个窗口，现在讲两个有用的，现在没用到以后再说，一个是command window，你可以在把一些计算啊，画图啊等等的命令一条一条的输入，然后求取结果，呵呵，比如现在我们来解决世界上最简单但最有争议的问题，在命令窗口里输入1+1然后按回车，你可以看到小麦对这个问题所给出的答案。

《1.2.3 几类特殊的矩阵变换》教案1教学目标1． 理解可以用矩阵来表示平面中常见的几何变换，掌握恒等、伸压、反射、旋转、投影、切变变换的矩阵表示及其几何意义2．理解二阶矩阵对应的几何变换是线性变换，了解单位矩阵3.了解恒等、伸压、反射、旋转、投影、切变变换这六个变换之间的关系教学重难点了解并掌握几种特殊的矩阵变换，可以简单的运用。

教学过程1．理解可以用矩阵来表示平面中常见的几何变换，掌握恒等、伸压、反射、旋转、投影、切变变换的矩阵表示及其几何意义（１）一般地，对于平面向量变换T ，如果变换规则为T ：⎥⎦⎤⎢⎣⎡y x →⎥⎦⎤⎢⎣⎡''y x =⎥⎦⎤⎢⎣⎡++dy cx by ax ，那么根据二阶矩阵与平面列向量在乘法规则可以改写为T ：⎥⎦⎤⎢⎣⎡y x →⎥⎦⎤⎢⎣⎡''y x =⎥⎦⎤⎢⎣⎡d c b a ⎥⎦⎤⎢⎣⎡y x 的矩阵形式，反之亦然（a 、b 、c 、d ∈Ｒ）由矩阵Ｍ确定的变换，通常记为T M ,根据变换的定义，它是平面内点集到自身的一个映射，平面内的一个图形它在T M ,的作用下得到一个新的图形.在本节中研究的变换包括恒等变换、伸压变换、反射变换、旋转变换、投影变换、切变变换等六个变换．（２）由矩阵M=⎥⎦⎤⎢⎣⎡1001确定的变换T M 称为恒等变换，这时称矩阵M 为恒等变换矩阵或单位矩阵，二阶单位矩阵一般记为E.平面是任何一点（向量）或图形，在恒等变换之下都把自己变为自己.（３）由矩阵M=⎥⎦⎤⎢⎣⎡100k 或M=⎥⎦⎤⎢⎣⎡k 001)0k (>确定的变换T M 称为（垂直）伸压变换，这时称矩阵M=⎥⎦⎤⎢⎣⎡100k 或M=⎥⎦⎤⎢⎣⎡k 001伸压变换矩阵． 当M=⎥⎦⎤⎢⎣⎡100k 时确定的变换将平面图形作沿x 轴方向伸长或压缩,当1k >时伸长,当1k 0<<时压缩.变换T M 确定的变换不是简单地把平面上的点(向量) 沿x 轴方向“向下压”或“向外伸”,它是x 轴方向伸长或压缩,以1k 0<<为例，对于x 轴上方的点向下压缩，对于x 轴下方的点向上压缩，对于x 轴上的点变换前后原地不动．当M=⎥⎦⎤⎢⎣⎡k 001时确定的变换将平面图形作沿y 轴方向伸长或压缩,当1k >时伸长,当1k 0<<时压缩．在伸压变换之下，直线仍然变为直线，线段仍然变为线段．恒等变换是伸压变换的特例，伸压变换多与三角函数图象的变换联系起来研究． （４）将一个平面图形变为关于定直线或定点对称的平面图形的变换矩阵称为反射变换矩阵，对应的变换称为反射变换，关于定直线或定点对称的反射又分别称为轴反射和中心反射，定直线称为反射轴，定点称为反射点．反射变换是轴对称变换、中心对称变换的总称.在中学里常研究的反射变换有： 由矩阵M １=⎥⎦⎤⎢⎣⎡-1001确定的变换是关于x 轴的轴反射变换，由矩阵M ２=⎥⎦⎤⎢⎣⎡-1001确定的变换是关于y 轴的轴反射变换,由矩阵M ３=⎥⎦⎤⎢⎣⎡--1001确定的变换是关于原点的中心反射变换．由矩阵M ４=⎥⎦⎤⎢⎣⎡0110确定的变换是关于直线y=x 的轴反射变换． 学习反射变换要与函数图象的变换、解几中二次曲线变换的知识联系起来考虑.其实质是变换对纵横坐标产生的影响.（５）将一个平面图形绕一个定点旋转角α得到另一个平面图形的变换称为旋转变换，其中的角α叫做旋转角，定点称为旋转中心．当旋转中心为原点且逆时针旋转角α时旋转变换的变换矩阵为⎥⎦⎤⎢⎣⎡-ααααcos sin sin cos ．旋转变换只会改变几何图形的位置，不会改变几何图形的形状和大小，旋转中心在旋转过程中保持不变，图形的旋转由旋转中心和旋转角所确定．绕定点旋转180的变换相当于关于定点作中心反射变换．（６）将一个平面图投影到某条直线（或某个点）的变换称为投影变换，变换对应的矩阵称为投影变换矩阵，本节中主要研究的是由矩阵M １=⎥⎦⎤⎢⎣⎡0001，M ２=⎥⎦⎤⎢⎣⎡0101 ，M ３=⎥⎦⎤⎢⎣⎡1000确定的投影变换．需要注意的是投影变换是映射，但不是一一映射． （７）由矩阵M=⎥⎦⎤⎢⎣⎡101k 或⎥⎦⎤⎢⎣⎡101k 确定的变换称为切变变换，对应的矩阵称为切变变换矩阵．以⎥⎦⎤⎢⎣⎡101k 为例，矩阵⎥⎦⎤⎢⎣⎡101k 把平面上的点)y ,x (沿x 轴方向平移｜ky|个单位，当ky ＞０时沿x 轴正方向移动，当ky ＜０时沿x 轴负方向移动，当ky ＝０时原地不动，切变变换有如下性质：（１）x 轴上的点是不动点；（２）保持图形面积大小不变,点间的距离和夹角大小可以改变且点的运动是沿坐标轴方向进行的．切变变换的实质是横（纵坐标）成比例地运动.2．理解二阶矩阵对应的几何变换是线性变换，了解单位矩阵一般地，二阶非零矩阵对应变换把直线变为直线，把直线变为直线的变换叫做线性变换，本节中所研究的6种变换均为线性变换，在研究平面上多边形或直线在矩阵的变换作用后的图形时，只需考察顶点（或端点）的变化结果即可．3.了解恒等、伸压、反射、旋转、投影、切变变换这六个变换之间的关系如恒等变换可以看做伸压、旋转、切变变换的特殊情形;关于坐标原点的中心反射变换可以看做是绕原点作了)Z k ()1k 2(∈π+角度的旋转变换，它还可以看做是先作关于x 轴的反射再作关于y 轴的反射的复合; 绕原点作了β+α角度的旋转变换可以看做是先绕原点作了α角度的旋转变换再绕原点作了β角度的旋转变换等等.基础训练１、已知四边形ABCD 的顶点分别为A （-1，0），B （1，0），C （1，1），D （-1，1），四边形ABCD 在矩阵⎥⎦⎤⎢⎣⎡100a 变换作用下变成正方形，则a ＝（ ）. Ａ、21 Ｂ、2 Ｃ、3 Ｄ、31 2、已知矩阵M 1=⎥⎦⎤⎢⎣⎡1001，M 2=⎥⎦⎤⎢⎣⎡-1001，M 3=⎥⎦⎤⎢⎣⎡0101，则由M 1，M 2，M 3确定的变换分别是（ ）A 、恒等变换、反射变换、投影变换B 、恒等变换、投影变换、反射变换C 、投影变换、反射变换、恒等变换D 、反射变换、恒等变换、投影变换3、直线x+y=5在矩阵⎥⎦⎤⎢⎣⎡1100 对应的变换作用下得到的图形是（ ）A 、直线x+y=5 B 、直线y=5 C 、直线x=5 D 、点（0，54、将向量⎥⎦⎤⎢⎣⎡=12绕原点按逆时针方向旋转4π得到向量b ，则向量b 的坐标为=______________. 5、图中正方形ABCD 在由矩阵⎥⎦⎤⎢⎣⎡1011所确定变换的作用后的图形的 _____________.6、若直线y=4x-4在矩阵M 对应的伸压变换下变成另一条直线y=x-1，则 M=__________.解题指导例1、求圆C ：224x y +=在矩阵2001A ⎡⎤=⎢⎥⎣⎦对应的伸压变换下的曲线方程，并判断曲线的类型.解：设P(x,y)是圆C ：224x y +=上的任一点, P 1)y ,x (''是P(x,y) 在矩阵2001A ⎡⎤=⎢⎥⎣⎦对应的伸压变换下的曲线上的对应点 , 则⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡''y x y x y x 21002 即 ⎩⎨⎧='='y y x x 2,所以⎪⎩⎪⎨⎧'='=y y x x 2 代入224x y +=得 22''44x y += 方程221164x y +=表示的曲线为椭圆 点评：通过变换矩阵建立所求曲线上的点的坐标之间的关系是解决这类问题的关键． 例２、若曲线y=x 2（x≥0）在矩阵M 对应的反射变换作用下得到的曲线为y=x 2（x≤0），求矩阵M.解：由两曲线之间的关系知：矩阵M 对应的反射变换是以y 轴为轴的反射变换，所以M ＝⎥⎦⎤⎢⎣⎡-1001点评：这类问题在求解时应先确定两曲线之间的反射变换是中心对称反射变换还是是轴对称变换．如果是轴对称变换再进一步确定对称轴，进而写出变换矩阵．例３、若△ABC 在矩阵M 对应的旋转变换作用下得到△A′B′C′，其中A （0，0），B （1，3），C （0，2），A′（0，0）， C′（-3，1），试求矩阵M 并求B′的坐标.解、由题意旋转中心为原点，设逆时旋转角为α)20(πα≤≤， 则旋转变换矩阵为Ｍ＝⎥⎦⎤⎢⎣⎡-ααααcos sin sin cos ∴⎥⎦⎤⎢⎣⎡-ααααcos sin sin cos ⎥⎦⎤⎢⎣⎡20＝⎥⎦⎤⎢⎣⎡-13 ∴⎩⎨⎧=-=-1cos 23sin 2αα∴ 故而3πα= ∴Ｍ＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-21232321 设B′（x,y ）,则⎥⎦⎤⎢⎣⎡y x ＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-21232321⎥⎦⎤⎢⎣⎡31＝⎥⎦⎤⎢⎣⎡-31 ∴)3,1(B -'点评：逆时针旋转角为α时的旋转矩阵为⎥⎦⎤⎢⎣⎡-ααααcos sin sin cos ，若顺时针旋转角为α时，则将上述矩阵中的α换为－α即可．例４、已知在矩阵M 的作用下点A （1，2）变成了点A′（11，5），点B （3，-1）变成了点B′（5，1），点C （x ，0）变成了点C′（y ，2），求（1）矩阵M ；求（2）x 、y 值. 解： （1）设矩阵M=⎥⎦⎤⎢⎣⎡d c b a ，∴⎥⎦⎤⎢⎣⎡d c b a ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡51121，⎥⎦⎤⎢⎣⎡d c b a ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-1513 ∴⎪⎪⎩⎪⎪⎨⎧=-=-=+=+135352112d c b a d c b a ，解之得⎪⎪⎩⎪⎪⎨⎧====2143d c b a ，∴M=⎥⎦⎤⎢⎣⎡2143（2）由 ⎥⎦⎤⎢⎣⎡2143⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡20y x 得⎩⎨⎧==23x y x ∴⎩⎨⎧==62y x点评：求变换矩阵通常用待定系数法．例５、给定二阶矩阵M ，对任意向量 αβ和，证明：()M M M αβαβ+=+证明：设a b M c d ⎡⎤=⎢⎥⎣⎦，11x y α⎡⎤=⎢⎥⎣⎦ ，22x y β⎡⎤=⎢⎥⎣⎦ 121212121212()()()()()x x a x x b y y a b M y y c x x d y y c d αβ++++⎡⎤⎡⎤⎡⎤+==⎢⎥⎢⎥⎢⎥++++⎣⎦⎣⎦⎣⎦121122121122x x ax by ax by a b a b M M y y cx dy cx dy c d c d αβ++⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=+=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦1212121212121212()()()()ax ax by by a x x b y y cx cx dy dy c x x d y y ++++++⎡⎤⎡⎤==⎢⎥⎢⎥++++++⎣⎦⎣⎦得证点评：更一般地，可以证明：λλλλM M M 2121)(+=+，其中21,λλ为任意实数。

MATLAB王春兴编物理与电子科学学院2009.9第一章MATLAB简介MA TLAB的原意为MATrix LABoratory,即矩阵实验室，是由在数值线性代数领域颇有影响的Cleve Moler博士首创的。

后来由Moler博士等一批数学家和软件专家组建了MathWorks软件公司，专门从事MATLAB的扩展与改进。

MA TLAB不仅具有强大的数值计算能力，而且具有数据图示功能和符号运算功能。

特别是大量的工具箱，扩展了应用领域，是高校学生、教师、科研人员和工程计算人员的最好选择，是数学建模必不可少的工具。

1.1MATLAB的主要特点1．功能强大MATLAB以复数矩阵作为基本编程单元，可以方便地处理诸如矩阵变换及运算、多项式运算、微积分运算、线性与非线性方程求解、常微分方程求解、偏微分方程求解、插值与拟合、特征值问题、统计及优化问题。

2．语言简单MATLAB语句书写简单，表达式的书写如同在稿纸中演算一样，允许用户以数学形式的语言编写程序，控制语句同C语言相近，并提供了强大的帮助功能。

3．扩充能力强MATLAB本身就像一个解释系统，用户可以方便地看到函数的源程序，也可以方便地开发自己的程序。

另外，MATLAB可以方便地和FORTRAN、C等语言进行接口，还和Maple有很好的接口。

4．编程易从形式上看，MATLAB程序文件是一个纯文本文件，扩展名为M，调试方便。

1.2MATLAB的窗口1．启动MATLAB2．工具栏3．命令窗口MATLAB的输入命令和输出结果的窗口，在这里输入的命令会立即执行并输出结果。

可用UP键盘将以前执行的命令调出。

1.3MATLAB的通用命令1.管理命令和函数：2.管理变量和工作空间3.控制命令窗口4.使用文件和工作环境5.启动和退出MA TLAB第二章数值计算2.1数字及运算1．数值MA TLAB中采用十进制数，并可用科学表示法，虚数用i或j 表示。

5 -39 0.0025 1.52e-20 6.9e13 3.0i -3+4i浮点数的范围大致为10-308~10308。

c语言s形矩阵S形矩阵是一种特殊的矩阵形式，它的元素按照S形排列。

在C语言中，我们可以通过使用循环和条件语句来实现S形矩阵的生成。

首先，我们需要确定矩阵的大小。

假设我们要生成一个n行m列的S形矩阵，那么我们需要定义一个n行m列的二维数组来存储矩阵的元素。

接下来，我们可以使用两层循环来遍历矩阵的每个元素。

外层循环控制行数，内层循环控制列数。

在每次循环中，我们需要判断当前元素的位置，以确定应该赋予什么值。

具体来说，我们可以使用条件语句来判断当前元素的位置。

如果当前元素的行数是奇数，那么我们可以直接将列数赋值给当前元素。

如果当前元素的行数是偶数，那么我们需要将列数与矩阵的列数相减再赋值给当前元素。

下面是一个生成S形矩阵的C语言代码示例：```c#include <stdio.h>void generateSMatrix(int n, int m) {int matrix[n][m];int i, j;for (i = 0; i < n; i++) {for (j = 0; j < m; j++) {if (i % 2 == 0) {matrix[i][j] = j + 1;} else {matrix[i][j] = m - j;}}}for (i = 0; i < n; i++) {for (j = 0; j < m; j++) {printf("%d ", matrix[i][j]);}printf("\n");}}int main() {int n, m;printf("请输入矩阵的行数和列数："); scanf("%d %d", &n, &m);generateSMatrix(n, m);return 0;}```在上面的代码中，我们首先定义了一个`generateSMatrix`函数，该函数接受两个参数n和m，分别表示矩阵的行数和列数。

奇偶矩阵知识点奇偶矩阵概述奇偶矩阵是指矩阵中每个元素的值为奇数或偶数的矩阵。

在数学中，奇偶矩阵有着一些特殊的性质和应用。

本文将介绍奇偶矩阵的定义、性质以及一些实际应用。

什么是奇偶矩阵？奇偶矩阵是由整数构成的矩阵，其中矩阵中的每个元素都是奇数或偶数。

换句话说，奇偶矩阵中不存在奇偶元素混合的情况。

例如，以下是一个3x3的奇偶矩阵的示例：1 2 34 5 67 8 9从上面的示例中可以看出，该矩阵中的每个元素都是奇数或偶数。

奇偶矩阵的性质奇偶矩阵具有一些有趣的性质，下面列举了其中几个常见的性质：性质1：奇偶矩阵的转置仍然是奇偶矩阵如果一个矩阵是奇偶矩阵，那么它的转置矩阵也是奇偶矩阵。

这是因为转置矩阵只是将原始矩阵的行和列进行交换，并不改变元素的奇偶性。

性质2：奇偶矩阵的和仍然是奇偶矩阵如果两个矩阵都是奇偶矩阵，那么它们的和也是一个奇偶矩阵。

这是因为奇数加奇数得到偶数，偶数加偶数还是偶数。

性质3：奇偶矩阵的乘积可能不是奇偶矩阵如果两个矩阵都是奇偶矩阵，它们的乘积不一定是奇偶矩阵。

乘法涉及到对应元素的相乘，而乘积的奇偶性取决于相乘的两个元素的奇偶性。

奇偶矩阵的应用奇偶矩阵在实际中有一些应用。

以下是其中几个常见的应用：应用1：图像处理奇偶矩阵可以用于图像处理中的滤波操作。

滤波器通常是由奇偶矩阵表示的，通过将滤波器应用于图像矩阵，可以实现去噪、边缘检测等图像处理操作。

应用2：密码学奇偶矩阵可以用于密码学中的加密和解密算法。

通过将明文矩阵与密钥矩阵进行奇偶运算，可以生成密文矩阵。

解密时，再将密文矩阵与密钥矩阵进行奇偶运算，可以还原出明文矩阵。

应用3：编码理论奇偶矩阵在编码理论中也有重要应用。

例如，校验矩阵是一种特殊的奇偶矩阵，用于检测和纠正传输中的错误。

总结奇偶矩阵是由整数构成的矩阵，其中每个元素的值为奇数或偶数。

奇偶矩阵具有一些特殊的性质，如转置仍然是奇偶矩阵，和仍然是奇偶矩阵，但乘积可能不是奇偶矩阵。

奇偶矩阵在图像处理、密码学和编码理论等领域有着重要的应用。