第九讲——卷积码的维特比译码和卷积码的性能分析

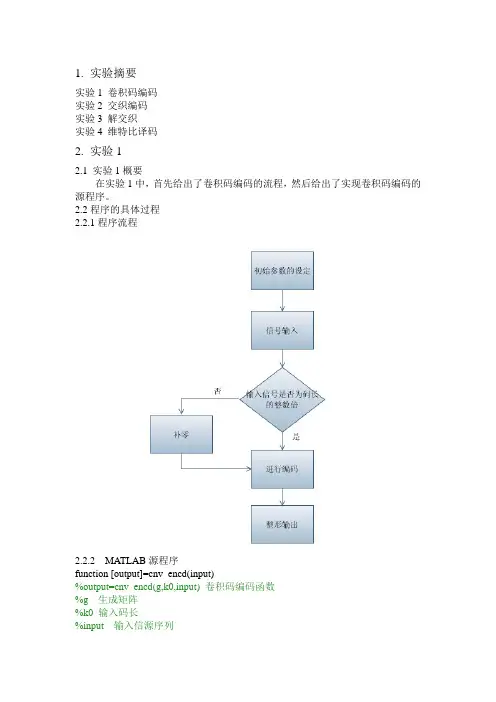
1.实验摘要实验1 卷积码编码实验2 交织编码实验3 解交织实验4 维特比译码2.实验12.1 实验1概要在实验1中，首先给出了卷积码编码的流程，然后给出了实现卷积码编码的源程序。

2.2程序的具体过程2.2.1程序流程2.2.2MATLAB源程序function [output]=cnv_encd(input)%output=cnv_encd(g,k0,input) 卷积码编码函数%g 生成矩阵%k0 输入码长%input 输入信源序列%output 输出卷积编码序列g=[1 1 1;1 0 1];%编码矩阵k0=1;input=[1 1 0 1];if rem(length(input),k0)>0input=[input,zeros(size(1:k0-rem(length(input),k0)))];endn=length(input)/k0;if rem(size(g,2),k0)>0error('Error,g is not of the right size.')endli=size(g,2)/k0;n0=size(g,1);u=[zeros(size(1:(li-1)*k0)),input,zeros(size(1:(li-1)*k0))];u1=u(li*k0:-1:1);for i=1:n+li-2u1=[u1,u((i+li)*k0:-1:i*k0+1)];enduu=reshape(u1,li*k0,n+li-1);output=reshape(rem(g*uu,2),1,n0*(n+li-1));3.实验23.1 实验2概要在实验2中，给出了两种交织编码的过程—卷积交织和循环等差交织，然后给出了实现这两种交织编码的源程序。

3.2程序的具体过程3.2.1程序流程3.2.2MATLAB源程序（1）卷积交织function [aa]=jiaozhi(bb,n)%jiaozhi.m 卷积交织函数n=28; %分组长度%bb 卷积交织前原分组序列%aa 卷积交织后分组序列%序号重排方式：cc=[123171151721;82241812628;159****9137;22161042620 14 ];%交织矩阵bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28]; for i=1:naa(i)=bb(cc(i));end（2）循环等差交织function [aa]=jiaozhi_nocnv(bb,n)%jiaozhi_nocnv.m 循环等差交织函数n=28; %分组长度%bb 循环等差交织前原分组序列%aa 循环等差交织后还原分组序列%序号重排方式：bb=[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 ];j=1;for i=1:nj=rem(j+5-1,n)+1; %序号重排方式迭代算法aa(n+1-i)=bb(j);end3.2.3程序说明交织码通常表示为（M，N），分组长度L=MN，交织方式用M行N列的交织矩阵表示。

编号：《DSP技术与应用》课程论文卷积码的维特比译码的分析与实现论文作者姓名：______ ______作者学号：___ ______所在学院：所学专业：_____ ___导师姓名职称：__ _论文完成时间： _目录摘要： (1)0 前言 (2)1 理论基础 (2)1.1信道理论基础 (2)1.2差错控制技术 (3)1.3纠错编码 (4)1.4线性分组码 (5)2 卷积码编码 (7)2.1 卷积码概要 (7)2.2 卷积码编码器 (8)2.3卷积码的图解表示 (8)2.4 卷积码的解析表示 (11)3 卷积码的译码 (14)3.1 维特比译码 (15)3.2 代数译码 (17)3.3 门限译码 (18)4 维特比译码器实现 (18)4.1 TMS320C54 系列DSP概述 (18)4.2 Viterbi译码器的DSP实现 (19)4.3 实现结果 (21)5 结论 (21)参考文献 (22)II卷积码的维特比译码的分析与实现摘要：针对数据传输过程中的误码问题，本文论述了提高数据传输质量的一些编码及译码的实现问题。

自P.Elias 首次提出卷积码编码以来，这一编码技术至今仍显示出强大的生命力。

在与分组码同样的码率R 和设备复杂性的条件下，无论从理论上还是从实际上均己证明卷积码的性能至少不比分组码差，且实现最佳和准最佳译码也较分组码容易。

目前，卷积码已广泛应用在无线通信标准中，其维特比译码则利用码树的重复性结构，对最大似然译码算法进行了简化。

本文所做的主要工作：首先对信道编码技术进行了研究，根据信道中可能出现的噪声等问题对卷积码编码方法进行了主要阐释。

其次，对卷积码维特比译码器的实现算法进行了研究，完成了译码器的软件设计。

最后，结合实例，采用DSP芯片实现卷积码的维特比译码算法的仿真和运行。

关键词：卷积码维特比译码DSPConvolutional codes and Viterbi decoding analysis andrealizationZhang Yi-Fei(School of Physics and Electronics, Henan University, Henan Kaifeng 475004, China)Abstract:Considering the error bit problem during data transmission,this thesis discussed some codings and decoders,aiming at enhancing transmission performance. From P.Elias first gave the concept of convolutional code, it has show its’ great advantage. Under the same condition and the same rate of block code, the performance of convolutional code is better than block code, and it’s easier to implement the best decoding.Convolutional codes have been widely used in wireless communication standards, the Viterbi decoding using the repetitive structure of the code tree, the maximum likelihood decoding algorithm has been simplified. Major work done in this article: First, the channel coding techniques have been studied, the main interpretation of the convolutional code encoding method according to the channel may be noise and other issues.Secondly, the convolutional code Viterbi decoder algorithm has been studied, the software design of the decoder.Finally, with examples, simulation and operation of the DSP chip convolutional codes, Viterbi decoding algorithm.1Key words:convolutional code Vltebri decoder DSP0 前言随着数据处理、计算机通信、卫星通信以及高速数据通信网的飞速发展，用户对数据传输的可靠性提出了越来越高的要求，因此如何在保证数据传输速率的前提下，提高传输数据的可靠性，就成为一个迫切需要解决的问题。

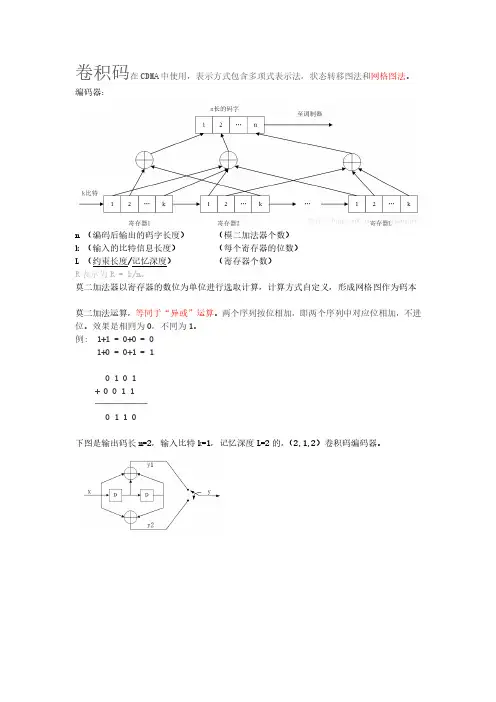
卷积码在CDMA中使用，表示方式包含多项式表示法，状态转移图法和网格图法。

编码器：n （编码后输出的码字长度）（模二加法器个数）k （输入的比特信息长度）（每个寄存器的位数）L （约束长度/记忆深度）（寄存器个数）R表示为R = k/n。

莫二加法器以寄存器的数位为单位进行选取计算，计算方式自定义，形成网格图作为码本莫二加法运算，等同于“异或”运算。

两个序列按位相加，即两个序列中对应位相加，不进位。

效果是相同为0，不同为1。

例: 1+1 = 0+0 = 01+0 = 0+1 = 10 1 0 1+ 0 0 1 1──────0 1 1 0下图是输出码长n=2，输入比特k=1，记忆深度L=2的，（2,1,2）卷积码编码器。

如编码序列“0 1 1 0 0”在图中的序列如下：汉明距离两个二进制数之间进行逐位对比，得到不同的个数如1000，与1100为1，与1110为2，与1111为3维特比算法综合状态之间的转移概率和前一层各状态的概率情况计算出概率最大的状态转换路径，从而推断出隐含状态的序列的情况。

的分支度量（汉明距离）。

其中有两条路径的分支量度为0。

3.寻找最大似然路径 - 译码过程维特比算法的关键点在于，接收机可以使用分支度量和先前计算的路径度量递推地计算当前状态的路径度量。

初始时，状态00代价为0，其它状态代价为正无穷（∞）。

算法的主循环由两个主要步骤组成：首先计算下一时刻监督比特序列的分支度量，然后计算该时刻各状态的路径度量。

路径度量的计算可以认为是一个“加-比-选”的过程1)将分支度量与上一时刻状态的路径度量相加。

2)每一状态比较来自前一时刻状态可达到的所有路径（只有两条这样的路径进行比较）3)每一状态删除其余到达路径，选择最小度量的路径保留（称为幸存路径/存活路径）若进入某个状态的部分路径中，有两条路径的度量值相等，则可以任选其一作为幸存路径。

下图显示了维特比译码的过程。

此例接收到的位序列为11 10 11 00 01 10（偷偷告诉你:这是有误码的信息）此时，产生了具有相同路径度量的四个不同路径，通向这四个状态的任一路径都是可能发送的比特序列（它们都具有度量为2的汉明距离）。

卷积编码和Viterbi译码摘要本文的目的是向读者介绍了前向纠错技术的卷积编码和Viterbi译码。

前向纠错的目的（FEC）的是改善增加了一些精心设计的冗余信息，正在通过信道传输数据的通道容量。

在添加这种冗余信息的过程称为信道编码。

卷积编码和分组编码是两个主要的渠道形式编码。

简介前向纠错的目的（FEC）的是改善增加了一些精心设计的冗余信息，正在通过信道传输数据的通道容量。

在添加这种冗余信息的过程称为信道编码。

卷积编码和分组编码是两个主要的渠道形式编码。

卷积码串行数据操作，一次一个或数位。

分组码操作比较大（通常，多达几百个字节的情侣）消息块。

有很多有用的分组码和卷积多种，以及接收解码算法编码信息的DNA序列来恢复原来的各种数据。

卷积编码和Viterbi译码前向纠错技术，是一种特别适合于在其中一个已损坏的发射信号加性高斯白噪声（AWGN）的主要通道。

你能想到的AWGN信道的噪声，其电压分布也随着时间的推移，可以说是用高斯，或正常，统计分布特征，即一钟形曲线。

这个电压分布具有零均值和标准差这是一个信号与噪声比接收信号的信噪比（SNR）函数。

让我们承担起接收到的信号电平是固定的时刻。

这时如果信噪比高，噪声标准偏差小，反之亦然。

在数字通信，信噪比通常是衡量Eb /N的它代表噪声密度双面能源每比特除以之一。

卷积码通常是描述使用两个参数：码率和约束长度。

码率k/n，是表示为比特数为卷积编码器（十一）信道符号卷积编码器输出的编码器在给定的周期（N）的数量之比。

约束长度参数，钾，表示该卷积编码器的“长度”，即有多少K位阶段提供饲料的组合逻辑，产生输出符号。

K是密切相关的参数米，这表明有多少位的输入编码器周期被保留，用于编码后第一次在卷积编码器输入的出现。

的m参数可以被认为是编码器的记忆长度。

在本教程中，并在此示例的源代码，我集中精力率1 / 2卷积码。

Viterbi译码是一种两个卷积编码与解码，其他类型的算法类型的顺序解码。

卷积码编码和维特比译码的原理、性能与仿真分析1.引言卷积码的编码器是由一个有k位输入、n位输出，且具有m位移位寄存器构成的有限状态的有记忆系统，通常称它为时序网络。

编码器的整体约束长度为v,是所有k个移位寄存器的长度之和。

具有这样的编码器的卷积码称作[n,k,v]卷积码。

对于一个（n,1,v）编码器，约束长度v等于存储级数m.卷积码是由k个信息比特编码成n（n>k）比特的码组，编码出的n比特码组值不仅与当前码字中的k个信息比特值有关，而且与其前面v个码组中的v*k个信息比特值有关。

卷积码有三种译码方式：序列译码、门限译码和概率译码。

其中，概率译码根据最大似然译码原理在所有可能路径中求取与接收路径最相似的一条路径，具有最佳的纠错性能，维特比译码是概率译码中极重要的一种方式。

序列译码和门限译码则不一定能找出与接收路径最相似的一条路径。

不同于维特比译码，门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于（m+1）个接收分组，而不是基于整个接收序列。

与维特比译码所使用的对数似然量度不同，序列译码所使用的量度为Fano量度。

在接收序列受扰严重的情况下，序列译码的计算量大于维特比译码所需的固定计算量，虽然序列译码要求的平均计算次数通常小于维特比译码。

在采用并行处理的情况下，维特比译码的速度会优于序列译码。

在同样码率和存储级数的条件下，门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式，本文选取生成多项式为561,753的（2,1,8）卷积码对硬判决的性能进行分析，并依据维特比译码的原理以及卷积码的特性，对卷积码编码和维特比译码过程在加性高斯白噪声（AWGN）信道下进行仿真，并且根据仿真结果对维特比译码（硬判决）的结果进行分析。

由于卷积码的生成可以看做一个马尔科夫过程，因此，不同状态间的转移概率对描述这个过程有极关键的作用。

本文则基于MATLAB对不同状态间的转移概率进行求解，从而更准确地分析维特比译码的性能。

卷积码的维特比译码卷积编码器自身具有网格结构，基于此结构我们给出两种译码算法：Viterbi 译码算法和BCJR 译码算法。

基于某种准则，这两种算法都是最优的。

1967 年，Viterbi 提出了卷积码的Viterbi 译码算法，后来Omura 证明Viterbi 译码算法等效于在加权图中寻找最优路径问题的一个动态规划（Dynamic Programming）解决方案，随后，Forney 证明它实际上是最大似然（ML，Maximum Likelihood）译码算法，即译码器选择输出的码字通常使接收序列的条件概率最大化。

BCJR 算法是1974 年提出的，它实际上是最大后验概率（MAP，Maximum A Posteriori probability）译码算法。

这两种算法的最优化目标略有不同：在MAP 译码算法中，信息比特错误概率是最小的，而在ML 译码算法中，码字错误概率是最小的，但两种译码算法的性能在本质上是相同的。

由于Viterbi 算法实现更简单，因此在实际应用比较广泛，但在迭代译码应用中，例如逼近Shannon 限的Turbo 码，常使用BCJR 算法。

另外，在迭代译码应用中，还有一种Viterbi 算法的变种：软输出Viterbi 算法（SOV A，Soft-Output Viterbi Algorithm），它是Hagenauer 和Hoeher 在1989 年提出的。

为了理解Viterbi 译码算法，我们需要将编码器状态图按时间展开（因为状态图不能反映出时间变化情况），即在每个时间单元用一个分隔开的状态图来表示。

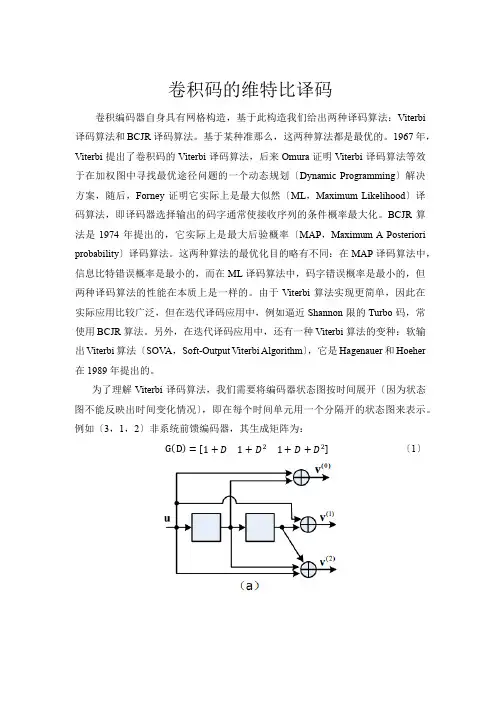
例如（3，1，2）非系统前馈编码器，其生成矩阵为：G(D)=[1+D1+D21+D+D2]（1）图1 （a）（3，1，2）编码器（b）网格图（h＝5）假定信息序列长度为h＝5，则网格图包含有h＋m＋1＝8 个时间单元，用0 到h＋m＝7 来标识，如图1（b）所示。

假设编码器总是从全0 态S0 开始，又回到全0 态，前m＝2 个时间单元对应于编码器开始从S0“启程”，最后m＝2 个时间单元对应于向S0“返航”。

2.7.卷积码分组码是把k个信息比特的序列编成n个比特的码组，每个码组的n-k个校验位仅与本码组的k个信息位有关，而与其他码组无关。

为了达到一定的纠错能力和编码效率，分组码的码组长度一般都比较大。

编译码时必须把整个信息码组存储起来，由此产生的译码时延随n的增加而增加。

卷积码是另外一种编码方法，它也是将k个信息比特编成n个比特，但k和n通常很小，特别适合以串行形式进行传输，时延小。

与分组码不同，卷积码编码后的n个码元不仅与当前段的k个信息有关，还与前面的N-1段信息有关，编码过程中互相关联的码元个数为nN。

卷积码的纠错性能随N的增加而增大，而差错率随N的增加而指数下降。

在编码器复杂性相同的情况下，卷积码的性能优于分组码。

但卷积码没有分组码那样严密的数学分析手段，目前大多是通过计算机进行好码的搜索。

2.7.1.卷积码的结构和描述一、卷积码的一般结构卷积码编码器的形式如图所示，它包括：一个由N段组成的输入移位寄存器，每段有k个，共Nk个寄存器；一组n个模2和相加器，一个由n级组成的输出移位寄存器。

对应于每段k个比特的输入序列，输出n个比特。

由上图可以看到，n个输出比特不仅与当前的k个输入信息有关，还与前（N-1）k个信息有关。

通常将N称为约束长度，（有的书的约束长度为Nn）。

常把卷积码记为：（n，k，N），当k=1时，N-1就是寄存器的个数。

二、卷积码的描述描述卷积码的方法有两类：图解法和解析表示。

图解法包括：树图、状态图、网格图解析法包括：矩阵形式、生成多项式形式。

以如下的结构说明各种描述方法。

1、树图根据上图，我们可以得到下表：我们可以画出如下的树状图：2、 状态图3、 网格图例1， 输入为1 1 0 1 1 1 0，输出为： 11 01 01 00 01 10 014、 生成多项式表示 定义],,[1211101g g g g=，],,[2221202g g g g=则上述结构为71=g，52=g，这里用8进制表示21,g gabcd⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2101211101],,[m m m g g g c ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2102221202],,[m m m g g g c定义2212111011)(DD Dg D g g D g ++=++=2222212021)(DDg D g g D g +=++=则输入信息,...,,210b b b 的多项式为....)(332210++++=b D b D b b D M那么我们可以得到输出)()()(11D g D M D C = )()()(22D g D M D C =最终输出是)(),(21D C D C的相同次数项的排列。

卷积码的维特比译码卷积编码器自身具有网格构造，基于此构造我们给出两种译码算法：Viterbi 译码算法和BCJR 译码算法。

基于某种准那么，这两种算法都是最优的。

1967 年，Viterbi 提出了卷积码的Viterbi 译码算法，后来Omura 证明Viterbi 译码算法等效于在加权图中寻找最优途径问题的一个动态规划〔Dynamic Programming〕解决方案，随后，Forney 证明它实际上是最大似然〔ML，Maximum Likelihood〕译码算法，即译码器选择输出的码字通常使接收序列的条件概率最大化。

BCJR 算法是1974 年提出的，它实际上是最大后验概率〔MAP，Maximum A Posteriori probability〕译码算法。

这两种算法的最优化目的略有不同：在MAP 译码算法中，信息比特错误概率是最小的，而在ML 译码算法中，码字错误概率是最小的，但两种译码算法的性能在本质上是一样的。

由于Viterbi 算法实现更简单，因此在实际应用比较广泛，但在迭代译码应用中，例如逼近Shannon 限的Turbo 码，常使用BCJR 算法。

另外，在迭代译码应用中，还有一种Viterbi 算法的变种：软输出Viterbi 算法〔SOV A，Soft-Output Viterbi Algorithm〕，它是Hagenauer 和Hoeher 在1989 年提出的。

为了理解Viterbi 译码算法，我们需要将编码器状态图按时间展开〔因为状态图不能反映出时间变化情况〕，即在每个时间单元用一个分隔开的状态图来表示。

例如〔3，1，2〕非系统前馈编码器，其生成矩阵为：G(D)=[1+D1+D21+D+D2]〔1〕图1 〔a〕〔3，1，2〕编码器〔b〕网格图〔h＝5〕假定信息序列长度为h＝5，那么网格图包含有h＋m＋1＝8 个时间单元，用0 到h＋m＝7 来标识，如图1〔b〕所示。

假设编码器总是从全0 态S0 开始，又回到全0 态，前m＝2 个时间单元对应于编码器开始从S0“启程〞，最后m＝2 个时间单元对应于向S0“返航〞。

卷积码编码维特比译码实验设计报告SUN一、实验目的掌握卷积码编码和维特比译码的基本原理，利用了卷积码的特性, 运用网格图和回溯以得到译码输出。

二、实验原理1.卷积码是由连续输入的信息序列得到连续输出的已编码序列。

其编码器将k个信息码元编为n个码元时，这n个码元不仅与当前段的k个信息有关，而且与前面的（m-1）段信息有关（m为编码的约束长度）。

2.一般地，最小距离d表明了卷积码在连续m段以内的距离特性，该码可以在m个连续码流内纠正(d-1)/2个错误。

卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。

3. 维特比译码算法基本原理是将接收到的信号序列和所有可能的发送信号序列比较，选择其中汉明距离最小的序列认为是当前发送序列。

卷积码的Viterbi 译码是根据接收码字序列寻找编码时通过网格图最佳路径的过程,找到最佳路径即完成了译码过程,并可以纠正接收码字中的错误比特。

4.所谓“最佳”, 是指最大后验条件概率:P( C/ R) = max [ P ( Cj/ R) ] , 一般来说, 信道模型并不使用后验条件概率,因此利用Beyes 公式、根据信道特性出结论:max[ P ( Cj/ R) ]与max[ P ( R/ Cj) ]等价。

考虑到在系统实现中往往采用对数形式的运算,以求降低运算量,并且为求运算值为整数加入了修正因子a1 、a2 。

令M ( R/ Cj) = log[ P ( R/ Cj) ] =Σa1 (log[ P( Rm/ Cmj ) ] + a2) 。

其中, M 是组成序列的码字的个数。

因此寻找最佳路径, 就变成寻找最大M( R/ Cj) , M( R/ Cj) 称为Cj 的分支路径量度,含义为发送Cj 而接收码元为R的似然度。

5.卷积码的viterbi译码是根据接收码字序列寻找编码时通过网格图最佳路径的过程，找到最佳路径即完成了译码过程并可以纠正接收码字中的错误比特。

三、实验代码#include<stdio.h>#include "Conio.h"#define N 7#include "math.h"#include <stdlib.h>#include<time.h>#define randomize() srand((unsigned)time(NULL))encode(unsigned int *symbols, /*编码输出*/unsigned int *data, /*编码输入*/unsigned int nbytes, /*nbytes=n/16,n为实际输入码字的数目*/unsigned int startstate /*定义初始化状态*/)////////////////////////////////////////////////////////////////////////////卷积码编码///////////////////////////////////////////////////////////////////////////////{unsigned int j;unsigned int input,a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;for(j=0;j<nbytes;j++){input=*data;data++;*symbols = input^a1^a2^a3^a6; //c1(171)symbols++;*symbols = input^a2^a3^a5^a6; //c2(133)symbols++;a2=a1;a1=input;}return 0;}int trandistance(int m, int state1, int state2)/*符号m与从state1到state2时输出符号的汉明距离,如果state1无法到state2则输出度量值为100*/{int c;int sym,sym1,sym2;sym1=((state2>>1)&1)^(state2&1)^(state1&1);sym2=((state2>>1)&1)^(state1&1);sym=(sym1<<1) | sym2;if ( ((state1&2)>>1)==(state2&1))c=((m&1)^(sym&1))+(((m>> 1)&1)^((sym >> 1)&1));elsec=10000;return(c);}int traninput(int a,int b) /*状态从a到b时输入卷积码的符号*/{int c;c=((b&2)>>1);return(c);}int tranoutput(int a,int b) /*状态从a到b时卷积码输出的符号*/{int c,s1,s2;s1=(a&1)^((a&2)>>1)^((b&2)>>1);s2=(a&1)^((b&2)>>1);c=(s1<<1)|s2;return(c);}////////////////////////////////////////////////////////////////////////////维特比译码///////////////////////////////////////////////////////////////////////////////void viterbi(int initialstate, /*定义解码器初始状态*/int *viterbiinput, /*解码器输入码字序列*/int *viterbioutput /*解码器输出码字序列*/){struct sta /*定义网格图中每一点为一个结构体,其元素包括*/ {int met; /*转移到此状态累计的度量值*/int value; /*输入符号*/struct sta *last; /*及指向前一个状态的指针*/};struct sta state[4][N];struct sta *g,*head;int i,j,p,q,t,r,u,l;for(i=0;i<4;i++) /* 初始化每个状态的度量值*/for(j=0;j<N;j++)state[i][j].met=0;for(l=0;l<4;l++){state[l][0].met=trandistance(*viterbiinput,initialstate,l);state[l][0].value=traninput(initialstate,l);state[l][0].last=NULL;}viterbiinput++; /*扩展第一步幸存路径*/for(t=1;t<N;t++){for(p=0;p<4;p++){state[p][t].met=state[0][t-1].met+trandistance(*viterbiinput,0,p);state[p][t].value=traninput(0,p);state[p][t].last=&state[0][t-1];for(q=0;q<4;q++){if(state[q][t-1].met+trandistance(*viterbiinput,q,p)<state[p][t].met){state[p][t].met=state[q][t-1].met+trandistance(*viterbiinput,q,p);state[p][t].value=traninput(q,p);state[p][t].last=&state[q][t-1];}}}viterbiinput++;} /*计算出剩余的幸存路径*/r=state[0][N-1].met; /*找出n步后度量值最小的状态准备回溯路由*/g=&state[0][N-1];for(u=N;u>0;u--) /*向前递归的找出最大似然路径*/{*(viterbioutput+(u-1))=g->value;g=g->last;}/* for(u=0;u<8;u++)*(viterbioutput+u)=state[u][2].met; */ /*此行程序可用于检测第n列的度量值*/}void decode(unsigned int *input, int *output,int n){int viterbiinput[100];int j;for(j=0;j<n+2;j++){viterbiinput[j]=(input[j*2]<<1)|input[j*2+1];}viterbi(0,viterbiinput,output);}void main(){unsigned intencodeinput[100],wrong[10]={0,0,0,0,0,0,0,0,0,0},encodeoutput[100];int n=5,i,m,j=0,decodeinput[100],decodeoutput[100];randomize();for(i=0; i<n; i++)encodeinput[i]=rand()%2;encodeinput[n]= encodeinput[n+1]=0;encode(encodeoutput,encodeinput,n+2,0);printf("the input of encoder is :\n"); //信息源输入的信息码（随机产生）for(i=0;i<n; i++)printf("%2d",encodeinput[i]);printf("\n");printf("the output of encoder is :\n"); //编码之后产生的卷积码for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");printf("please input the number of the wrong bit\n"); //信道传输收到干扰而产生的错误码scanf("%d",&m);printf("please input the positions of the wrong bit(0-9)\n");for(i=0;i<m;i++){scanf("%d",&wrong[m]);if(encodeoutput[wrong[m]]==0)encodeoutput[wrong[m]]=1;elseencodeoutput[wrong[m]]=0;}printf("the input of decoder is :\n");for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");decode(encodeoutput,decodeoutput,n+2);printf("the output of decoder is :\n");for(i=0;i<n;i++)printf("%2d",decodeoutput[i]);printf("\n");for(i=0;i<n;i++){if(encodeinput[i]!=decodeoutput[i])j++;}printf("the number of incorrect bit is:%d\n",j);}四、实验总结（1）了解实验原理，分析实验所占数组变量很重要，也是相对考虑较多的；（2）对于读写文件，通过本实验更加熟悉；（3）记录实验程序最佳路径是本实验的难点；。

基于FPGA的卷积码Viterbi译码器性能研究卷积码是一种前向纠错控制(Forward Error Control，FEC)编码方式，其特点是接收端根据接收码字自动检测和纠正信道传输引入的错误。

由于FEC方式不需要反馈信道，译码实时性比较好，控制电路比较简单，因此，卷积码在卫星通信、数字话音通信等实时性要求较高的场合有着重要的应用。

卷积码的编译码器的实现可以利用EDA技术，采用硬件描述语言VerilogHDL或VHDL等进行FPGA 编程设计，这种实现方式在集成度、可靠性和灵活性方面可达到比较满意的效果。

在设计卷积码FPGA 译码器时，需要考虑所用芯片规格、成本、系统计算量以及时延等因素。

目前现有文献多对卷积码的实现进行研究，而对译码算法中参数设置情况研究较少。

本文采用VHDL语言，在设计实现卷积码FPGA编译码器的基础上，通过仿真对Viterbi译码算法中的参数进行了讨论。

1 Viterbi译码算法Viterbi译码算法由维特比在1967年提出。

Viterbi译码算法实质上是最大似然译码，他巧妙利用编码网格图的特殊结构，从而降低计算的复杂性。

例如图1即为(2，1，2)卷积码的网格图。

这里(n，k，m)分别指码组宽度n，信息元个数k和编码存储度m，称m+1=N为编码约束度。

该算法思想是：计算网格图上在时刻L到达各个状态的路径和接收序列之间的相似度；在形成的多条路径中，去除不可能成为最大似然选择对象的网格图上的路径，即，如果有两条路径到达同一状态，则具有最佳量度的路径被选中，称为幸存路径。

对所有状态都将进行这样的路径选择操作，译码器不断在网格图上深入，通过去除可能性最小的路径实现判决。

Viterbi译码算法步骤如下：(1)用数组p(i，j)，c(i，j)描述网格图结构。

p(i，j)表示到达状态i的第j个前状态，其对应的码字是(i，j)。

(2)计算第L时刻接收码RL相对于各码字睁相似度，亦称作分支量度BM(Branch Metric)。

卷积码编码和维特比译码的性能对比1.引言卷积码的编码器是由一个有k位输入、n位输出，且具有m位移位寄存器构成的有限状态的有记忆系统，通常称它为时序网络。

编码器的整体约束长度为v,是全部k个移位寄存器的长度之和。

具有这样的编码器的卷积码称作[n,k,v]卷积码。

对于一个（n,1,v）编码器，约束长度v等于存储级数m.卷积码是由k个信息比特编码成n（nk）比特的码组，编码出的n比特码组值不仅与当前码字中的k个信息比特值有关，而且与其前面v个码组中的v*k个信息比特值有关。

卷积码有三种译码方式：序列译码、门限译码和概率译码。

其中，概率译码依据最大似然译码原理在全部可能路径中求取与接收路径最相像的一条路径，具有最佳的纠错性能，维特比译码是概率译码中极重要的一种方式。

序列译码和门限译码则不肯定能找出与接收路径最相像的一条路径。

不同于维特比译码，门限译码与序列译码所需的计算量是可变的且对于给定信息分组的最终判决仅仅基于（m+1）个接收分组，而不是基于整个接收序列。

与维特比译码所使用的对数似然量度不同，序列译码所使用的量度为Fano量度。

在接收序列受扰严峻的状况下，序列译码的计算量大于维特比译码所需的固定计算量，虽然序列译码要求的平均计算次数通常小于维特比译码。

在采纳并行处理的状况下，维特比译码的速度会优于序列译码。

在同样码率和存储级数的条件下，门限译码的性能比维特比译码低大约3dB.维特比译码的数据输出方式有硬判决及软判决两种方式，本文选取生成多项式为561,753的（2,1,8）卷积码对硬判决的性能进行分析，并依据维特比译码的原理以及卷积码的特性，对卷积码编码和维特比译码过程在加性高斯白噪声（AWGN）信道下进行仿真，并且依据仿真结果对维特比译码（硬判决）的结果进行分析。

由于卷积码的生成可以看做一个马尔科夫过程，因此，不同状态间的转移概率对描述这个过程有极关键的作用。

本文则基于MATLAB对不同状态间的转移概率进行求解，从而更精确地分析维特比译码的性能。