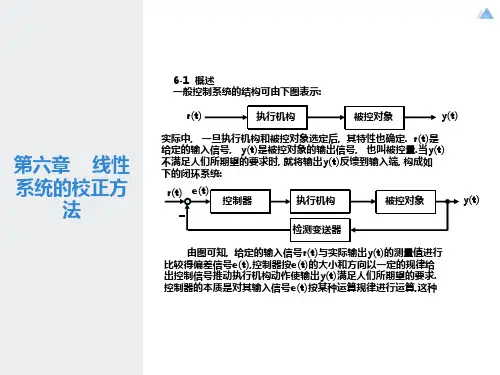
第六章线性系统的校正方法
- 格式:ppt
- 大小:7.92 MB
- 文档页数:87



第6章线性系统的校正方法。
重点与难点一、基本概念1.理想的频率特性系统开环频率特性与系统时域指标之间有一定的关系。
对于二阶系统而言,相位裕量/、截止频率必与时域指标(超调量。
%、调节时间4)有确定性关系。
对高阶系统而言,/,纭都可以粗略估计高阶系统的响应特性。
相位裕量越大,系统阶跃响应的超调量和调节时间4就越小;?也近似与4成反比关系。
因此,理想的频率特性应该有较大的相位裕量;希望响应快的系统就应该有大一点的。
闭环系统(单位反应)的频率特性有如下关系:|。
| (| a \< 1)(当有积分环节时。
=1)= ,(通常称为低频段)(6.1)201g|G(j7w) | co »(通常称为高频段)式中G(./7y)为开环频率特性。
因此,假设希望系统有较强的抗高频干扰能力,”应该小, 而且201g|G(八y)|要衰减快。
如果频率特性用渐近线方法描述,理想的频率特性应该在也.处以-20dB/dec斜率穿越OdB 线,才能获得较大的相位裕量。
综合上所述,理想的频率特性应有积分环节且开环增益大,以满足稳态误差的要求; 在截止频率0c的频域(通常称为中频段),应以一20dB/dec的斜率穿越OdB线,并占有足够宽的频带,以保证系统具备较大的相位裕量;在。
>〉9•的高频段,频率特性应该尽快衰减,以消减噪声影响。
2.系统的校正当系统频率特性不满足理想的频率特性指标(通常的指标体系为:闭环谐振峰值M,.、谐振频率/,、带宽频率口〃或开环频率特性的相位裕量/、截止频率0,、开环增益K、幅值裕量等)时,需要引入校正网络,使新系统的频率特性满足要求。
设计校正网络参数通常用频率校正方法。
当希望系统的闭环极点到达要求时,需要加入某一校正网络以改变闭环极点。
通常采用根轨迹校正方法。
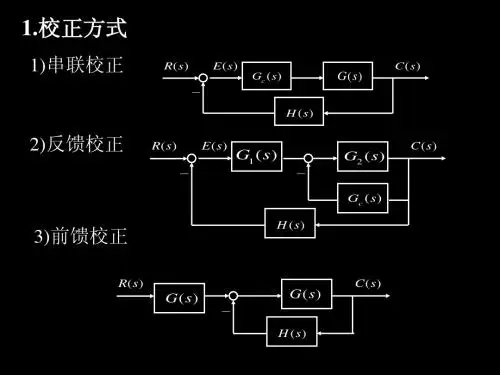
3.校正方式通常,在电口]区间内,假设对数幅频、相频特性是单调的,那么0G(幼RT80。
假设g>%,那么8G(例)<—1800。