第3讲一维频率分析和交叉表分析
- 格式:ppt
- 大小:404.50 KB
- 文档页数:45

多变量描述统计分析交叉表分析法一、交叉表分析法的概念交叉表(交叉列联表) 分析法是一种以表格的形式同时描述两个或多个变量的联合分布及其结果的统计分析方法,此表格反映了这些只有有限分类或取值的离散变量的联合分布。
当交叉表只涉及两个定类变量时,交叉表又叫做相依表。
交叉列联表分析易于理解,便于解释,操作简单却可以解释比较复杂的现象,因而在市场调查中应用非常广泛。
频数分布一次描述一个变量,交叉表可同时描述两个或更多变量。
交叉表法的起点是单变量数据,然后依研究目的将这些数据分成两个或多个细目。
下面是一个描述交叉表法应用的例子。
某保险公司对影响保户开车事故率的因素进行调研,并对各种因素进行了交叉表分析。
表1 驾驶员的事故率类别比率,%无事故61至少有一次事故39样本总数,人17800从初始表1中可以看出,有61%的保险户在开车过程中从未出现过事故。
然后,在性别基础上分解这个信息,判断是否在男女驾车者之间有差别。
这样就出现了二维交叉表2。
表2 男女驾驶员的事故率类别男,%女,%无事故5666至少有一次事故4434样本总数,人93208480这个表的结果令男士懊恼,因为他们的事故率较女士驾车时涉及的事故率要高。
但人们会提出这样的疑问而否定上述判断的正确性,即男士的事故多,是因为他们驾驶的路程较长。
这样就引出第三个因素"驾驶距离",于是出现了三维交叉表3。
表3 不同驾驶距离下的事故率类别男,%女,%驾驶距离>1万公里<1万公里>1万公里<1万公里无事故51735073至少有一次事49275027故样本总数,人7170215024306050结果表明,男士驾驶者的高事故率是由于他们的驾驶距离较女士长,但并没有证明男士和女士哪个驾驶得更好或更谨慎,仅证明了驾车事故率只与驾驶距离成正比,而与驾驶者的性别无关。
二、两变量交叉列联表分析例如,研究城镇居民在某地的居住时间与其对当地百货商场的熟悉程度之间的关系,对“居住时间”和“熟悉程度”这两个变量进行交叉列联分析。

交叉分析法怎么分析交叉分析法是一种常用的数据分析方法,通过对不同因素之间的关系进行交叉比较和分析,帮助研究者发现变量之间的联系和差异。
本文将介绍交叉分析法的基本概念和步骤,并以具体案例进行说明。
一、交叉分析法概述交叉分析法(Cross-Tabulation Analysis)也被称为列联表分析(Contingency Table Analysis),是一种定量分析方法,用来研究两个或更多变量之间的关系。
通过构建列联表,对不同变量之间的交叉频数进行统计和比较,可以揭示变量之间的关联性和差异性。
二、交叉分析法步骤1. 确定研究问题:明确研究问题并选择需要分析的变量。
例如,假设我们想研究消费者对不同手机品牌的偏好与性别之间的关系。
2. 构建列联表:根据所研究的变量,构建列联表(也称为交叉表)。
横列为一个变量的不同水平(例如手机品牌),纵列为另一个变量的不同水平(例如性别)。
在交叉点上填写交叉频数。
3. 计算频数和比例:根据列联表,计算每个交叉点上的频数和比例。
频数表示各组别的数量,比例表示各组别所占比例。
4. 绘制图表:通过绘制图表,直观地展示不同变量之间的关系。
常用的图表包括堆叠柱状图、簇状柱状图、饼图等。
5. 进行统计检验:为了验证变量之间的关系是否显著,可以进行统计检验,如卡方检验。
卡方检验可以检验各组别之间的差异是否由随机因素引起。
6. 分析结果和讨论:根据交叉分析的结果,进行结果分析和讨论。
解释变量之间的关系和差异,并提出合理的解释和解决方案。
三、交叉分析方法案例以消费者对不同手机品牌的偏好与性别之间的关系为例,进行交叉分析。
我们调查了300名消费者,结果如下表所示:--------------------------------------------------| Apple | Samsung | Huawei | Others--------------------------------------------------男性 | 50 | 30 | 20 | 10--------------------------------------------------女性 | 20 | 40 | 50 | 20--------------------------------------------------根据上表,我们可以计算出各组别的频数和比例,如下所示:--------------------------------------------------| Apple | Samsung | Huawei | Others--------------------------------------------------男性 | 50 | 30 | 20 | 10--------------------------------------------------女性 | 20 | 40 | 50 | 20--------------------------------------------------| 70(23%) | 70(23%) | 70(23%) | 30(10%)--------------------------------------------------通过绘制堆叠柱状图,我们可以直观地看到不同手机品牌在不同性别中的偏好程度。

一维信号的频率谱和相位谱是信号处理中常用的分析工具。
频率谱描述了信号中各个频率成分的幅度大小。
对于一维信号,可以通过傅里叶变换将其分解为多个不同频率的正弦波的叠加。
傅里叶变换的结果就是信号的频率谱,它表示了每个正弦波的幅度随频率的变化情况。
相位谱描述了信号中各个频率成分的相位信息。
相位是描述信号波形在时间上相对位置的量,它决定了波的形状和位置。
对于一维信号,其相位谱表示了每个正弦波的相位随频率的变化情况。
在实际应用中,频率谱和相位谱对于信号处理和分析非常重要。
例如,在音频处理中,可以通过频率谱分析来提取信号中的音调信息;在图像处理中,可以通过傅里叶变换将图像从空间域转换到频域,从而进行滤波、去噪等操作。
需要注意的是,频率谱和相位谱是相互依存的,它们共同构成了信号的完整频域表示。
在处理和分析信号时,通常需要同时考虑这两个方面。


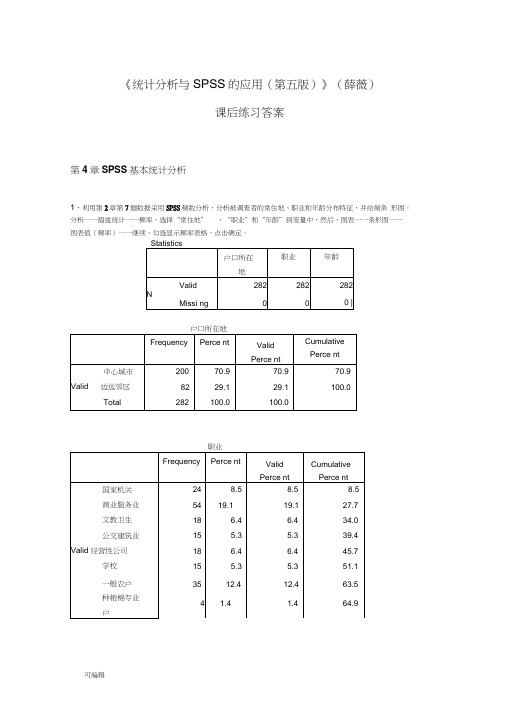
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第4章SPSS基本统计分析1、利用第2章第7题数据采用SPSS频数分析,分析被调查者的常住地、职业和年龄分布特征,并绘制条形图。
分析一一描述统计一一频率,选择“常住地”,“职业”和“年龄”到变量中,然后,图表一一条形图一一图表值(频率)一一继续,勾选显示频率表格,点击确定。
种果菜专业户10 3.5 3.568.4工商运专业户3412.112.180.5退役人员17 6.0 6.086.5金融机构3512.412.498.9现役军人3 1.1 1.1100.0 Total282100.0100.0Freque ncy Perce nt ValidPerce nt Cumulative Percent20岁以下4 1.4 1.4 1.420~35 岁14651.851.853.2 Valid 35~50 岁9132.332.385.5 50岁以上4114.514.5100.0Total282100.0100.0户口所在曲C-中3川毗吨户口分析:本次调查的有效样本为282份。
常住地的分布状况是:在中心城市的人最多,有200人,而在边远郊区只有82人;职业的分布状况是:在商业服务业的人最多,其次是一般农户和金融机构;年龄方面:在35-50岁的人最多。
由于变量中无缺失数据,因此频数分布表中的百分比相同。
2、利用第2章第7题数据,从数据的集中趋势、离散程度以及分布形状等角度,分析被调查者本次存款金额的基本特征,并与标准正态分布曲线进行对比。
进一步,对不同常住地储户存款金额的基本特征进行对比分析。
分析一一描述统计一一描述,选择存款金额到变量中。
点击选项,勾选均值、标准差、方差、最小值、最大值、范围、偏度、峰度、按变量列表,点击继续一一确定。
分析:由表中可以看出,有效样本为282份,存(取)款金额的均值是4738.09,标准差为10945.09,峰度系数为33.656,偏度系数为5.234。
第1篇一、引言随着社会经济的发展和科技的进步,问卷调查作为一种重要的数据收集方法,在各个领域得到了广泛的应用。
本次调研旨在通过对问卷数据的分析,了解某一特定领域或问题的现状、趋势和潜在需求,为相关决策提供数据支持。
以下是对本次问卷调研报告的数据分析。
二、调研背景本次调研以某城市居民的生活满意度为研究对象,旨在了解居民在生活各方面的满意程度,为政府和企业提供决策依据。
调研对象为该城市居民,采用随机抽样方式,共发放问卷500份,回收有效问卷450份,有效回收率为90%。
三、数据分析方法本次调研采用描述性统计分析、交叉分析、相关性分析和因子分析等方法对问卷数据进行处理和分析。
1. 描述性统计分析:对问卷数据进行频数分析、百分比分析、均值分析等,以了解数据的集中趋势和离散程度。
2. 交叉分析:通过交叉表分析不同变量之间的关系,找出影响生活满意度的关键因素。
3. 相关性分析:运用皮尔逊相关系数分析变量之间的线性关系,找出影响生活满意度的主要因素。
4. 因子分析:将多个变量归纳为少数几个因子,以揭示变量之间的内在联系。
四、数据分析结果1. 描述性统计分析(1)性别比例:男性占比52%,女性占比48%。
(2)年龄分布:18-25岁占比20%,26-35岁占比30%,36-45岁占比25%,46-55岁占比15%,56岁以上占比10%。
(3)婚姻状况:已婚占比60%,未婚占比40%。
2. 交叉分析(1)性别与生活满意度:男性生活满意度均值为3.5,女性生活满意度均值为3.6,女性满意度略高于男性。
(2)年龄与生活满意度:随着年龄增长,生活满意度呈现上升趋势,46-55岁年龄段满意度最高。
(3)婚姻状况与生活满意度:已婚人群生活满意度均值为3.7,未婚人群生活满意度均值为3.4,已婚人群满意度高于未婚人群。
3. 相关性分析(1)性别与生活满意度:性别与生活满意度之间的相关系数为0.12,表明性别对生活满意度有一定影响,但影响程度较小。
dynamicreports 交叉表-概述说明以及解释1.引言1.1 概述动态报告是一种高度可定制和自动化生成的报告生成工具,可以通过使用动态报告库来创建丰富多样的报告,包括但不限于交叉表。
在数据分析和数据可视化领域,交叉表是一种常用的工具,用于展示不同变量之间的关系以及它们对结果的影响。
本文将重点介绍dynamicreports库中的交叉表功能,该库是一个功能强大的Java报告生成库,提供了丰富的报告生成选项和灵活的报告布局。
它可以帮助开发人员轻松地生成精美的报告,并且具有良好的扩展性和可定制性。
在本文中,我们将首先介绍动态报告的基本概念,包括其原理和使用方法。
随后,我们将详细介绍dynamicreports库的特点和功能,以及它为创建交叉表所提供的支持。
我们将解释交叉表的概念和应用,并展示如何使用dynamicreports库来创建交叉表报告。
在文章的结论部分,我们将总结动态报告的优势,包括其在报告生成方面的灵活性和效率。
同时,我们还将对dynamicreports库中的交叉表功能进行评价,并探讨未来的发展方向。
通过本文的阅读,读者将能够全面了解动态报告和交叉表的基本概念,以及如何使用dynamicreports库来创建交叉表报告。
同时,读者还可以深入了解该库的特点和功能,并探索其在数据分析和报告生成领域的应用价值。
1.2 文章结构本篇长文将按照以下结构进行组织和论述:第一部分是引言部分,主要对本文的研究对象进行概述,并介绍了文章的整体结构和目的。
引言部分将介绍动态报告和交叉表的基本概念,以及本文的研究目的。
第二部分是正文部分,主要围绕动态报告和交叉表展开讨论。
首先,将介绍动态报告的基本概念,包括其用途和特点。
然后,将详细介绍dynamicreports库,包括其功能和应用场景。
接着,将介绍交叉表的概念和应用,以及交叉表在数据分析中的重要性。
最后,将详细介绍dynamicreports库中的交叉表功能,包括如何创建和定制交叉表,以及如何使用它们进行数据分析和可视化。
对离散型数据进行分析的方法离散型数据是指可计数且只能取有限个数值的数据,如性别(男、女)、血型(A、B、O、AB)等。
对离散型数据进行分析,我们可以采用以下几种方法:1.频数分析(Frequency Analysis):频数分析是对离散型数据进行初步描述和总结的方法。
它通过计算每个取值的频数(即该取值出现的次数)来了解各个取值的分布情况。
根据频数可以计算频率或者百分比,以更直观地描述不同取值之间的差异。
2.数据可视化:可视化是离散型数据分析的重要手段,可以更直观地展示数据的分布情况和变化趋势。
对于离散型数据,我们可以使用条形图、饼图等来呈现不同取值的频数或百分比。
此外,还可以使用象形图(Pictographs)来以图像的形式展示数据,从而更容易理解。
3.交叉分析(Cross-tabulation):交叉分析是通过比较不同离散型变量的交叉组合来分析它们之间的关系。
通过构造交叉表,我们可以计算各组合的频数或百分比,进而探寻不同离散变量之间是否存在关联。
交叉分析常用于探索一些变量在不同条件下的分布差异,例如性别与收入水平之间的关系等。
4.卡方检验(Chi-square test):卡方检验是一种常用的统计方法,用于检验两个或多个离散型变量是否相关。
它比较实际观察值与理论期望值之间的差异程度,从而判断两个变量之间是否存在独立性或相关性。
卡方检验可以帮助我们确定两个离散变量之间的统计显著性水平,并得出结论。
5.列联表分析(Contingency table analysis):除了以上方法,对离散型数据进行分析还可以采用回归分析、聚类分析等统计方法。
需要根据具体的情况选择适合的分析方法,以得出准确、有意义的结论。
同时,数据预处理和合理选择变量也是离散型数据分析的重要环节,可以通过数据清洗、特征选择等手段提高分析结果的可靠性和解释性。