正比例第一课时

春中附小六年级数学导学案课题：正比例第一课时（课本19——20页）主备人：刘巧玲 审核人：段晚霞 时间：2013.2.2姓名： 组名： 评价等级： 学习目标：1．利用正比例解决一些简单的生活问题，感受正比例关系在生活中的广泛应用。

2．能根据正比例的意义，判断两个相关联的量是不是成正比例。

3．结合丰富的事例，认识正比例。

学习重点：1、 结合丰富的事例，认识正比例。

2、 能根据正比例的意义，判断两个相关联的量是不是成正比例。

学习难点：能根据正比例的意义，判断两个相关联的量是不是成正比例。

学习过程 一、温故知新1、一辆汽车匀速行驶，每小时行60千米.（1）由上面信息你可以找到哪些量?哪些量变量，哪些量是常量？（2）两变量之间存在什么样的关系？(3) 知识链接：像这样，一种量变化，另一种量也随着变化，我们就说这样的两种量是两种相关联的量2、练一练请说说哪两个变量是相关联的量？ （1）人的身高与体重 （2）人的长相与身高 （3）正方形的边长与周长 （4）人的身高与跳绳的速度（5）每袋米重50千克,米的袋数和重量 二、探究新知自学以下的内容，完成下列各题：在情境中感受两种相关联的量之间的变化规律。

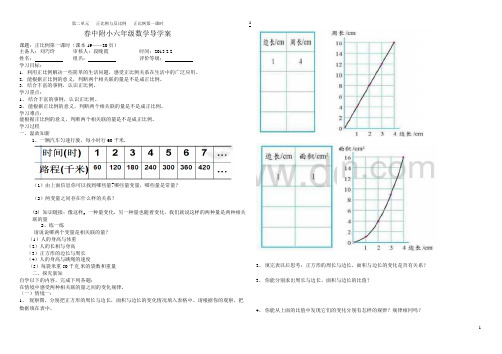
（一）情境一：1、 观察图，分别把正方形的周长与边长，面积与边长的变化情况填入表格中。

请根据你的观察，把数据填在表中。

2、 填完表以后思考：正方形的周长与边长，面积与边长的变化是否有关系？3、 你能分别求出周长与边长、面积与边长的比值？4、 你能从上面的比值中发现它们的变化分别有怎样的规律？规律相同吗？（二）情境二：1、一种汽车行驶的速度为90千米/小时。

汽车行驶的时间和路程如下： （P20页）请把下表填写完整。

2、 从表中你发现了什么规律？（三）情境三：1、一些人买一种苹果，购买苹果的质量和应付的钱数如下。

（P20页）2、把表填写完整。

3、从表中发现了什么规律：4、说说以上两个例子有什么共同的特点。

共同点： 5、正比例关系：像这样，时间增加，所走的路程也相应增加，而且路程与时间的比值（速度）相同。

六年级下册数学教案-正比例第一课时西师大版一、教学目标1. 让学生理解正比例的意义，掌握正比例的基本性质。

2. 培养学生运用正比例解决实际问题的能力。

3. 培养学生合作交流、动手操作的能力。

二、教学内容1. 正比例的定义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。

2. 正比例的判断方法：判断两种相关联的量是否成正比例，就看这两种量是否是对应的比值一定，如果是比值一定，就成正比例，如果不是比值一定或比值不一定，就不成正比例。

3. 正比例的运用：解决实际问题时，先根据正比例的意义，找出两种相关联的量，再根据正比例关系列式解答。

三、教学重点与难点1. 教学重点：正比例的意义及判断方法。

2. 教学难点：正比例在实际问题中的运用。

四、教具与学具准备1. 教具：多媒体课件、黑板、粉笔。

2. 学具：练习本、草稿纸、计算器。

五、教学过程1. 导入：通过生活中的实例，引出正比例的概念。

2. 新课：讲解正比例的定义、判断方法及运用。

3. 案例分析：分析几个典型的正比例案例，让学生理解正比例的意义。

4. 练习：让学生独立完成练习题，巩固正比例的知识。

5. 小组讨论：分组讨论，让学生在实际问题中运用正比例。

6. 课堂小结：总结本节课的主要内容，强调正比例在实际问题中的运用。

7. 作业布置：布置课后作业，让学生进一步巩固正比例知识。

六、板书设计1. 正比例的定义2. 正比例的判断方法3. 正比例的运用4. 典型案例5. 练习题七、作业设计1. 填空题：让学生填写正比例的定义、判断方法等相关内容。

2. 判断题：让学生判断给出的量是否成正比例。

3. 计算题：让学生解决实际问题，运用正比例关系列式计算。

4. 应用题：让学生根据正比例的意义，解决实际问题。

八、课后反思1. 学生对正比例的理解程度，是否掌握了正比例的定义、判断方法及运用。

19.2.1 正比例函数第1课时 正比例函数的概念一、知识回顾：1.函数的概念：在一个 过程中有 变量x 与y ，并且对于x 的 确定的值，y 都有 的值与其对应，那么我们就说x 是 ，y 是x 的 。

2. 表示函数的方法有：、 、3. 用描点法画函数图像的一般步骤为：、 、 、 。

二、新知探究：1.下列问题中，变量之间的对应关系是函数关系吗？如果是，请写出函数解析式：（1）圆的周长l 随半径r 的变化而变化．（2）铁的密度为7.8g/cm3,铁块的质量m （单位：g ）随它的体积V （单位：cm3）的变化而变化．（3）每个练习本的厚度为0.5cm ，一些练习本摞在一起的总厚度h （单位：cm ）随练习本的本数n 的变化而变化．（4）冷冻一个0℃的物体，使它每分钟下降2℃，物体温度T （单位：℃）随冷冻时间t （单位：min ）的变化而变化．2.思考：（1）认真观察以上出现的四个函数解析式，分别说出哪些是函数、常数和自变量．（2）这些函数解析式在结构上有什么共同特点？归纳：一般地，形如 （ ）的函数，叫做正比例函数，其中 叫做比例系数．三、针对训练。

1.在下列函数中，哪些是正比例函数？并指出正比例系数分别是多少.①y=x, ②y=6x 2, ③ y=2x , ④y=x -4， ⑤ ⑥y=-x ⑦2. 判定正误：下列说法正确的打“√”，错误的打“×”（1）若y=kx ，则y 是x 的正比例函数（ ）（2）若y=4x2，则y 是x 的正比例函数（ ）（3）若y=4(x -1)，则y 是x 的正比例函数（ ）（4）若y=4(x -1)+4，则y 是x 的正比例函数（ ）（5）若y=4(x -1) ，则y 是x -1的正比例函数（ ）3.2011年开始运营的京沪高速铁路全长1318千米，设列车的平均速度为300千米每小时。

考虑以下问题： x y 1-=x 2132)2(--=m x m y （1）乘高铁，从始发站北京南站到终点站上海站，约需多少小时？（保留一位小数）（2）京沪高铁的行程ykm 与时间th 之间满足函数关系吗？若满足请写出解析式。

六年级下册数学教案正比例第一课时西师大版教案：正比例一、教学内容今天我要向大家介绍的是正比例这一概念。

我们使用的教材是西师大版的六年级下册，我们将要学习的是第96页至第98页的内容。

这部分内容主要包括正比例的定义、正比例函数的图像以及如何判断两个相关联的量是否成正比例。

二、教学目标通过这一节课的学习，我希望大家能够掌握正比例的概念，理解正比例函数的图像特点，并能够运用正比例的知识解决实际问题。

三、教学难点与重点本节课的重点是正比例的概念和正比例函数的图像特点。

难点在于理解正比例的判断方法以及如何应用正比例解决实际问题。

四、教具与学具准备为了更好地讲解正比例，我准备了一些图片和实物，以及一些练习题，让大家能够通过实际例子更好地理解正比例的概念。

五、教学过程1. 实践情景引入：我拿出两根长度不同的尺子，让大家观察它们的形状。

请大家思考，这两根尺子的长度和它们的形状有什么关系？2. 讲解正比例概念：我向大家解释，如果两个相关联的量的比值始终保持不变，那么这两个量就成正比例。

我通过尺子的例子来让大家更好地理解这个概念。

3. 展示正比例函数图像：我向大家展示了一些正比例函数的图像，让大家观察它们的特征。

请大家思考，如何判断一个函数是否是正比例函数？4. 例题讲解：我给大家讲解了一道例题，让大家通过实际问题来运用正比例的知识。

题目是：小明每天步行上学，他的速度是每小时4公里，问小明步行上学需要多少时间？5. 随堂练习：我给大家布置了一些练习题，让大家能够通过实际例子来运用正比例的知识。

题目是：一辆汽车以每小时60公里的速度行驶，问这辆汽车行驶120公里需要多少时间？六、板书设计我在黑板上写下了正比例的定义和判断方法，以及正比例函数的图像特点。

这样让大家能够一目了然地看到正比例的关键信息。

七、作业设计我给大家布置了一道作业题：判断下列两种相关联的量是否成正比例，并说明理由。

题目是：一个人的体重和他的身高是否成正比例？八、课后反思及拓展延伸通过这一节课的学习，我发现大家对于正比例的概念有了更深入的理解，大家在实际问题中也能够运用正比例的知识。