北京市朝阳区2012届高三年级第一次综合练习(数学文科)

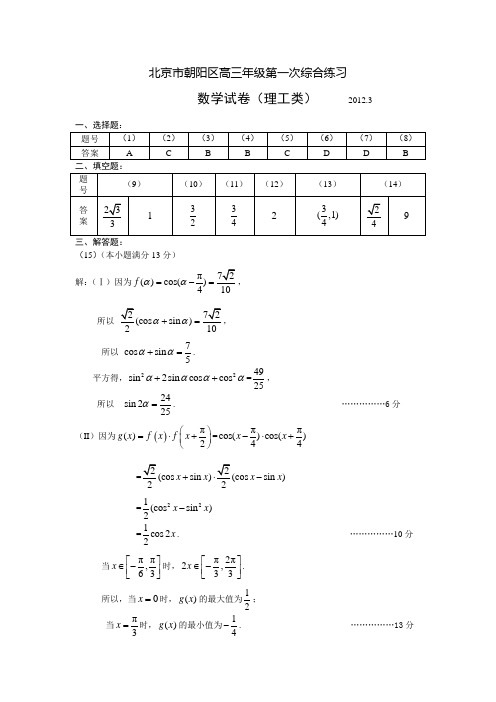
北京市朝阳区高三年级第一次综合练习数学试卷（理工类） 2012.3三、解答题：（15）（本小题满分13分）解：（Ⅰ）因为π()cos()410f αα=-=，所以(cos sin )210αα+=， 所以 7cos sin 5αα+=. 平方得，22sin 2sin cos cos αααα++=4925， 所以 24sin 225α=. ……………6分 （II ）因为()π()2g x f x f x ⎛⎫=⋅+⎪⎝⎭=ππcos()cos()44x x -⋅+=(cos sin )(cos sin )22x x x x +⋅- =221(cos sin )2x x - =1cos 22x . ……………10分当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2,33x ⎡⎤∈-⎢⎥⎣⎦. 所以，当0x =时，()g x 的最大值为12； 当π3x =时，()g x 的最小值为14-. ……………13分（16）（本小题满分13分） 解：（Ⅰ）依题意，0.0451000200,0.025*******a b =⨯⨯==⨯⨯=. ……………4分 （Ⅱ）设其中成绩为优秀的学生人数为x ，则350300100401000x ++=，解得：x =30， 即其中成绩为优秀的学生人数为30名. ……………7分（Ⅲ）依题意，X 的取值为0，1，2，2102403(0)52C P X C ===，1110302405(1)13C C P X C ===，23024029(2)52C P X C ===， 所以X 的分布列为350125213522EX =⨯+⨯+⨯=，所以X 的数学期望为2. ……………13分（17）（本小题满分14分）证明：（Ⅰ）取AD 的中点N ，连接MN,NF .在△DAB 中，M 是BD 的中点，N 是AD 的中点，所以1=2MN//AB,MN AB ， 又因为1=2EF//AB,EF AB ，所以MN//EF 且MN =EF .所以四边形MNFE 为平行四边形， 所以EM//FN .又因为FN ⊂平面ADF ，⊄EM 平面ADF ，故EM//平面ADF . …………… 4分 解法二：因为EB ⊥平面ABD ，AB BD ⊥，故以B 为原点，建立如图所示的空间直角坐标系-B xyz . ……………1分 由已知可得 (0,0,0),(0,2,0),(3,0,0),B A D3(3,-2,0),(,0,0)2C E F M （Ⅰ）3=((3,-2,0)2EM ,AD=u u u r u u u r， 设平面ADF 的一个法向量是()x,y,z n =.由0,0,AD AF n n ⎧⋅=⎪⎨⋅=⎪⎩u u u ru u u r 得32x -y =0,=0.⎧⎪⎨⎪⎩ 令y=3，则n =. 又因为3(=3+0-3=02EM n ⋅=⋅u u u r，所以EM n ⊥u u u r，又EM ⊄平面ADF ，所以//EM 平面ADF . ……………4分NCA F EBMD（Ⅱ）由（Ⅰ）可知平面ADF的一个法向量是n =. 因为EB ⊥平面ABD ，所以EB BD ⊥.又因为AB BD ⊥，所以BD ⊥平面EBAF .故(3,0,0)BD =u u u r是平面EBAF 的一个法向量.所以1cos <=2BD BD,BD n n n ⋅>=⋅u u u ru u u r u u u r，又二面角D-AF -B 为锐角， 故二面角D-AF -B 的大小为60︒. ……………10分 （Ⅲ）假设在线段EB 上存在一点P ，使得CP 与AF 所成的角为30︒.不妨设(0,0,t)P（0t ≤≤，则=(3,-2,-),=PC AF t u u u r u u u r.所以cos <PC AF PC,AF PC AF ⋅>==⋅u u u r u u u ru u u r u u u ru u u r u u u r ，2=，化简得35-=，解得0t =<.所以在线段EB 上不存在点P ，使得CP 与AF 所成的角为30︒.…………14分 （18）（本小题满分13分）解：因为2e (),1ax f x x =+所以222e (2)()(1)ax ax x a f x x -+'=+.（Ⅰ）当1a =时, 2e ()1xf x x =+,222e (21)()(1)x x xf x x -+'=+, 所以(0)1,f = (0)1f '=.所以曲线()y f x =在点(0,(0))f 处的切线方程为10x y -+=. ……………4分（Ⅱ）因为222222e (2)e ()(2)(1)(1)ax ax ax x a f x ax x a x x -+'==-+++， ……………5分 （1）当0a =时,由()0f x '>得0x <；由()0f x '<得0x >.所以函数()f x 在区间(,0)-∞单调递增, 在区间(0,)+∞单调递减. ……………6分 （2）当0a ≠时, 设2()2g x ax x a =-+，方程2()20g x ax x a =-+=的判别式2444(1)(1),a a a ∆=-=-+ ……………7分①当01a <<时，此时0∆>.由()0f x '>得x <,或x >；由()0f x '<得11x a a-+<<.所以函数()f x 单调递增区间是1(,a -∞和1()a ++∞,单调递减区间11(,a a +. ……………9分②当1a ≥时，此时0∆≤.所以()0f x '≥，所以函数()f x 单调递增区间是(,)-∞+∞. ……………10分 ③当10a -<<时，此时0∆>.由()0f x '>x <<；由()0f x '<得x <,或x >.所以当10a -<<时,函数()f x 单调递减区间是1(,a +-∞和1()a +∞,单调递增区间11(a a +-. ……………12分④当1a ≤-时, 此时0∆≤，()0f x '≤，所以函数()f x 单调递减区间是(,)-∞+∞. …………13分（19）（本小题满分14分）解: （Ⅰ）依题意，c =1b =，所以a == 故椭圆C 的方程为2213x y +=. ……………4分（Ⅱ）①当直线l 的斜率不存在时，由221,13x x y =⎧⎪⎨+=⎪⎩解得1,3x y ==±.不妨设A，(1,B ，因为132233222k k +=+=，又1322k k k +=，所以21k =，所以,m n 的关系式为213n m -=-，即10m n --=. ………7分 ②当直线l 的斜率存在时，设直线l 的方程为(1)y k x =-.将(1)y k x =-代入2213x y +=整理化简得，2222(31)6330k x k x k +-+-=. 设11(,)A x y ，22(,)B x y ，则2122631k x x k +=+,21223331k x x k -=+. ………9分 又11(1)y k x =-，22(1)y k x =-. 所以12122113121222(2)(3)(2)(3)33(3)(3)y y y x y x k k x x x x ----+--+=+=---- 12211212[2(1)](3)[2(1)](3)3()9k x x k x x x x x x ---+---=-++121212122(42)()6123()9kx x k x x k x x x x -++++=-++222222223362(42)6123131336393131k k k k k k k k k k k -⨯-+⨯++++=--⨯+++ 222(126)2.126k k +==+………12分所以222k =，所以2213n k m -==-，所以,m n 的关系式为10m n --=.………13分 综上所述，,m n 的关系式为10m n --=. ………14分 （20）（本小题满分13分）解：（Ⅰ）若0:0,1,1,3,0,0A ，则1:1,0,1,3,0,0A ；2:2,1,2,0,0,0A ； 3:3,0,2,0,0,0A ； 4:4,1,0,0,0,0A ； 5:5,0,0,0,0,0A ．若4:4,0,0,0,0A ，则 3:3,1,0,0,0A ； 2:2,0,2,0,0A ； 1:1,1,2,0,0A ；0:0,0,1,3,0A ． ………4分（Ⅱ）先证存在性，若数列001:,,,n A a a a L 满足0k a =及0(01)i a i k >≤≤-，则定义变换1T -，变换1T -将数列0A 变为数列10()T A -：01111,1,,1,,,,k k n a a a k a a -+---L L ．易知1T -和T 是互逆变换． ………5分 对于数列,0,0,,0n L 连续实施变换1T -（一直不能再作1T -变换为止）得,0,0,,0n L 1T -−−→1,1,0,,0n -L 1T -−−→2,0,2,0,,0n -L 1T-−−→3,1,2,0,,0n -L 1T -−−→L 1T-−−→01,,,n a a a L ，则必有00a =（若00a ≠，则还可作变换1T -）．反过来对01,,,n a a a L 作有限次变换T ，即可还原为数列,0,0,,0n L ，因此存在数列0A 满足条件．下用数学归纳法证唯一性：当1,2n =是显然的，假设唯一性对1n -成立，考虑n 的情形． 假设存在两个数列01,,,n a a a L 及01,,,n b b b L 均可经过有限次T 变换，变为,0,,0n L ，这里000a b ==，1212n n a a a b b b n +++=+++=L L 若0n a n <<，则由变换T 的定义，不能变为,0,,0n L ；若n a n =，则120n a a a ====L ，经过一次T 变换，有0,0,,0,n L T−−→1,1,,1,0L 由于3n ≥，可知1,1,,1,0L （至少3个1）不可能变为,0,,0n L ．所以0n a =，同理0n b =令01,,,n a a a L T−−→121,,,,n a a a '''L ，01,,,n b b b L T−−→121,,,,n b b b '''L ，则0nn a b ''==，所以1211n a a a n -'''+++=-L ，1211n b b b n -'''+++=-L ． 因为110,,,n a a -''L T−−−−→有限次-1,0,,0n L ，110,,,n b b -''L T−−−−→有限次-1,0,,0n L ，故由归纳假设，有i i a b ''=，1,2,,1i n =-L ． 再由T 与1T -互逆，有01,,,n a a a L T−−→111,,,,0n a a -''L ，01,,,n b b b L T−−→111,,,,0nb b -''L ，所以i i a b =，1,2,,i n =L ，从而唯一性得证． ………9分 （Ⅲ）显然i a i ≤(1,2,,)i n =L ，这是由于若对某个0i ，00i a i >，则由变换的定义可知，0i a通过变换，不能变为0．由变换T 的定义可知数列0A 每经过一次变换，k S 的值或者不变，或者减少k ，由于数列0A 经有限次变换T ，变为数列,0,,0n L 时，有0m S =，1,2,,m n =L ，所以m m S mt =(m t 为整数)，于是1m m m S a S +=+1(1)m m a m t +=++，0m a m ≤≤， 所以m a 为m S 除以1m +后所得的余数，即[](1)1mm m S a S m m =-++．………13分。

北京市昌平区2012届高三上学期期末考试试题（数学文）北京市朝阳区2012届高三上学期期末考试试题（数学文）北京市东城区2012届高三上学期期末教学统一检测（数学文）北京市房山区2012届高三上学期期末统测数学（文）试题北京市丰台区2012届高三上学期期末考试试题（数学文）北京市海淀区2012届高三上学期期末考试试题（数学文）北京市石景山区2012届高三上学期期末考试数学（文）试卷北京市西城区2012届高三上学期期末考试试题（数学文）2012年2月昌平区2011－2012学年第一学期高三年级期末质量抽测数 学 试 卷（文科） 2012 .1考生注意事项：1.本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分，满分150分，考试时间 120分钟．2.答题前，考生务必将学校、班级、考试编号填写清楚．答题卡上第一部分(选择题)必须用2B 铅笔作答，第二部分(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔．3.修改时，选择题用塑料橡皮擦干净，不得使用涂改液．请保持卡面整洁，不要折叠、折皱、破损．不得在答题卡上作任何标记．4.请按照题号顺序在各题目的答题区域内作答，未在对应的答题区域作答或超出答题区域的作答均不得分． 第Ⅰ卷（选择题 共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)1．设全集}7,5,3,1{=U ，集合}7,3,1{},5,3{==B A ，则()U A B ð等于A ．{5}B ．{3，5}C ．{1，5，7}D ．Φ2．21i -等于A ． 22i -B ．1i -C ．iD ．1i +3．“x y >”是“22x y>”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4.从3名男同学，2名女同学中任选2人参加体能测试，则选到的2名同学中至少有一名男同学的概率是A ．910B ．45C ．25D ．125.若某空间几何体的三视图如图所示，则该 几何体的体积是 A ．2 B ．4 C ．6. D ．8 6. 某程序框图如图所示，则输出的S =A ．120B ． 57C ．56D ． 267.某类产品按工艺共分10个档次，最低档次产品每件利润为8元.主视俯视同样工时，可以生产最低档产品60件，每提高一个档次将少生产3件产品.则获得利润最大时生产产品的档次是A.第7档次B.第8档次C.第9档次D.第10档次8. 一圆形纸片的圆心为点O ,点Q 是圆内异于O 点的一定点，点A 是圆周上一点.把纸片折叠使点A 与Q 重合，然后展平纸片，折痕与OA 交于P 点.当点A 运动时点P 的轨迹是 A ．圆 B ．椭圆 C ． 双曲线 D ．抛物线第Ⅱ卷（非选择题 共110分）填空题（本大题共6小题，每小题5分，共30分）．9.已知函数x x y cos sin = ，则函数的最小正周期是 .10.已知向量(2,1)=a ，10⋅=a b ， 7+=a b ，则=b .11.某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的 产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100)，[100，102)，[102，104)，[104，106] .已知样本中产品净重小于100克的个数是48，则a =___________ ；样本中净重在[98，104）的产品的个数是__________ .12. 已知双曲线122=-y m x 的右焦点恰好是抛物线x y 82=的焦点，则m = .13. 已知D是由不等式组0,0,x y x -≥⎧⎪⎨+≥⎪⎩所确定的平面区域，则圆224x y +=在区域D 内的弧长为_____________；该弧上的点到直线320x y ++=的距离的最大值等于__________ .14.设函数)(x f 的定义域为R ，若存在与x 无关的正常数M ，使|||)(|x M x f ≤对一切实数x 均成立，a则称)(x f 为有界泛函.在函数①x x f 5)(-=，②x x f 2sin )(=，③xx f )21()(=，④x x x f cos )(=中，属于有界泛函的有__________(填上所有正确的序号) .三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) 15.（本小题满分13分）在ABC ∆中，AA A cos cos 2cos 212-=．（I ）求角A 的大小；（II ）若3a =，sin 2sin B C =，求ABCS ∆．16．（本小题满分13分） 已知数列}{n a 是等差数列,22, 1063==a a ，数列}{n b 的前n 项和是nS ，且131=+n n b S .（I ）求数列}{n a 的通项公式；（II ）求证：数列}{n b 是等比数列；17.（本小题满分14分）如图在四棱锥P ABCD -中，底面ABCD 是正方形，ABCD PA 底面⊥，垂足为点A ，2==AB PA ,点M ，N 分别是PD ，PB 的中点．（I ）求证:ACM PB 平面// ； （II ）求证:⊥MN 平面PAC ；（III ）求四面体A MBC -的体积.18.(本小题满分13分)已知函数ax x x x f ++=1ln )(（a 为实数）.（I ）当0=a 时， 求)(x f 的最小值；（II ）若)(x f 在),2[+∞上是单调函数，求a 的取值范围.19.(本小题满分14分)已知椭圆C 的中心在原点，左焦点为(，离心率为23．设直线l 与椭圆C 有且只有一个公共点P ，记点P 在第一象限时直线l 与x 轴、y 轴的交点分别为B A 、，且向量+=.求： （I ）椭圆C 的方程；（II ）||的最小值及此时直线l 的方程.20. (本小题满分13分)M 是具有以下性质的函数()f x 的全体：对于任意s ，0t >，都有()0f s >，()0f t >，且()()()f s f t f s t +<+.（I ）试判断函数12()log (1)f x x =+，2()21x f x =-是否属于M ？（II ）证明：对于任意的0x >，0(x m m +>∈R 且0)m ≠都有[()()]0m f x m f x +->；（III ）证明：对于任意给定的正数1s >，存在正数t ，当0x t <≤时，()f x s <.昌平区2011－2012学年第一学期高三年级期末质量抽测 数学(文科)试卷参考答案及评分标准 2012.1一、选择题(本大题共8小题，每小题5分，共40分．)二、填空题(本大题共6小题，每小题5分，共30分．) 9．π 10. 26 11. 0.125；120 12. 313． 65π;5102+14. ① ② ④三、解答题(本大题共6小题，共80分)15.（本小题满分13分）解：（I ）由已知得：AA A cos cos )1cos 2(2122-=-，……2分.21cos =∴A ……4分 π<<A 0 ，.3π=∴A …………6分（II ）由C c B b sin sin = 可得：2sin sin ==c bC B ………7分∴ c b 2= …………8分214942cos 222222=-+=-+=c c c bc a c b A ………10分 解得：32b , 3==c ………11分2332333221sin 21=⨯⨯⨯==A bc S . ……13分16（本小题满分13分）解：（1）由已知⎩⎨⎧=+=+.225,10211d a d a 解得 .4,21==d a.244)1(2-=⨯-+=∴n n a n ………………6分（2）由于nn b S 311-=， ① 令n =1，得.31111b b -= 解得431=b ，当2≥n 时，11311---=n n b S ② －②得n n n b b b 31311-=- ， 141-=∴n n b b 又0431≠=b ,.411=∴-n n b b ∴数列}{n b 是以43为首项，41为公比的等比数列.……………………13分17.（本小题满分14分）证明：（I ）连接O BD AC MN MO MC AM BD AC = 且,,,,,,的中点分别是点BD PD M O ,, ACM PB PB MO 平面⊄∴,//∴ACM PB 平面//. …… 4分(II) ABCD PA 平面⊥ ，ABCD BD 平面⊂BD PA ⊥∴是正方形底面ABCDBD AC ⊥∴又A AC PA =⋂ PAC BD 平面⊥∴ ……7分在中PBD ∆，点M ，N 分别是PD ，PB 的中点．∴BD MN //PAC MN 平面⊥∴. …… 9分（III ）由h S V V ABC ABC M MBC A ⋅⋅==∆--31 ……11分PAh 21= ……12分 32212131=⋅⋅⋅⋅⋅=∴-PA AD AB V MBC A . ……14分18.(本小题满分13分)解：(Ⅰ) 由题意可知：0>x ……1分当0=a 时21)(x x x f -=' …….2分当10<<x 时，0)(<'x f 当1>x 时，0)(>'x f ……..4分故1)1()(m in ==f x f . …….5分(Ⅱ) 由222111)(x x ax a x x x f -+=+-='① 由题意可知0=a 时，21)(x x x f -=',在),2[+∞时，0)(>'x f 符合要求 …….7分② 当0<a 时，令1)(2-+=x ax x g 故此时)(x f 在),2[+∞上只能是单调递减0)2(≤'f 即04124≤-+a 解得41-≤a …….9分 当0>a 时，)(x f 在),2[+∞上只能是单调递增 0)2(≥'f 即,04124≥-+a 得41-≥a 故0>a …….11分综上),0[]41,(+∞⋃--∞∈a …….13分19. （本小题满分14分） 解：(Ⅰ)由题意可知3=c ，23==a c e ，所以2=a ，于是12=b ，由于焦点在x 轴上，故C 椭圆的方程为2214x y += ………………………………5分（Ⅱ）设直线l 的方程为：m kx y +=)0(<k ，),0(),0,(m B k mA -⎪⎩⎪⎨⎧=++=,14,22y x m kx y 消去y 得：012)41(222=-+++m kmx x k …………………7分直线l 与曲线C 有且只有一个公共点，0)1)(41(42222=-+-=∆m k m k即1422+=k m ① …………………… 9分 ∵OB OA OM +=222||m k m OM +=∴② ……………………11分将①式代入②得：||3OM ==当且仅当22-=k 时，等号成立，故min ||3OM =，此时直线方程为：03222=-+y x . …………………14分20（本小题满分13分）(Ⅰ)由题意可知，0)(,0)(,0)(,0)(2211>>>>t f s f t f s f 若)1(log )1(log )1(log 222++<+++t s t s 成立 则1)1)(1(++<++t s t s 即0<st与已知任意s ，0t >即0>st 相矛盾，故M x f ∉)(1； ……2分 若12222-<-++ts ts成立 则01222<--++ts t s即0)21)(12(<--t s s ，0t > 021,12<->∴t s 即0)21)(12(<--ts 成立 …..4分故M x f ∈)(2.综上，M x f ∉)(1，M x f ∈)(2. ……5分(II) 当0>m 时，)()()()(x f m f x f m x f >+>+ 0)()(>-+∴x f m x f 当0<m 时，)()()()()(m x f m f m x f m m x f x f +>-++>-+=0)()(<-+∴x f m x f故0)]()([ >-+x f m x f m . ……9分(III) 据（II ））上为增函数在（∞+.0)(x f ，且必有)(2)2(x f x f >（*） ①若s f <)1(，令1=t ，则t x ≤<0时 s x f <)(；②若,)1(s f >则存在*N ∈k ，使t f k 12)1(=<由（*）式可得s f f f kk k <<<<<-1)1(21)21(21)21(1即当s x f t x <≤<)(0时， 综①、②命题得证。

北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试数学试卷（文史类） 2011.11（考试时间120分钟 满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分注意事项：1．答第一部分前，考生务必将自己的姓名、考试科目涂写在答题卡上.考试结束时，将试题卷和答题卡一并交回.2．第一部分每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.第二部分不能答在试题卷上，请答在答题卡上.第一部分（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1.设集合{}260M x x x =+-<，{}13N x x =≤≤，则M N 等于（ ）A ．[)1,2B ．[]1,2C ．(]2,3D ．[]2,32. 已知向量a ，b 满足|a | = 8，|b | = 6， a ·b = 24，则a 与b 的夹角为（ ） A ．30︒ B ．60︒ C ．90︒ D ．120︒3. 已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示，则ω等于( ) A ．13 B ．1 C ．32D ．24.已知等差数列{}n a 的前n 项和为n S ，且369315a a a ++=，则11S 等于（ ）A ．78B ．66C ．55D ．335.命题“,sin 1x x ∀∈≤R ”的否定是（ ）A ．,sin 1x x ∃∈≥RB ．,sin 1x x ∀∈>RC ．,sin 1x x ∀∈≥RD ．,sin 1x x ∃∈>R 6. 函数x x x f ln )(+=的零点所在的大致区间为（ ）A ．()0,1B ．()1,2C ．()1,eD ．()2,e 7. “1a >”是“对任意的正数x ，不等式21a x x+≥成立”的 （ ）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件8.设集合{}0123,,,S A A A A =，在S 上定义运算⊕：i j k A A A ⊕=，其中k 为i j +被4除的余数，,0,1,2,3i j =，则使关系式0()i i j A A A A ⊕⊕=成立的有序数对(,)i j 的组数为（ ）A ．4B ．3C ．2D ．1第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在题中横线上. 9.已知π3(,π),sin ,25αα∈=则tan α= .10.已知等比数列{}n a 各项均为正数,前n 项和为n S ，若22a =，1516a a =，则3a = ；5S = ．11. 在A B C ∆中，角,,A B C 所对的边分别为,,a b c ．若5,2a b c ===，则cos B = .12. 在A B C ∆中，已知(2,1)A B = ，(3,)AC k =()k ∈R ，则BC =__；若90B ∠=︒，则k =__ _．13.已知函数2,20,()2cos ,0.x x f x x x ⎧-≤≤=⎨<≤π⎩若方程()f x a =有解，则实数a 的取值范围是 ．14.设函数()1f x x α=+（α∈Q ）的定义域为[][],,b a a b -- ，其中0a b <<，且()f x 在[],a b 上的最大值为6，最小值为3，则()f x 在[],b a --上的最大值与最小值的和为 .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本小题满分13分）设集合{|(1)0,M x x x a =--<a ∈R },集合2{|230}N x x x =--≤.（Ⅰ）当1a =时，求M N ；（Ⅱ）若M N ⊆,求实数a 的取值范围.16. （本小题满分13分）已知向量a =(sin ,cos())x x π-，b =(2cos ,2cos )x x ，函数()1f x =⋅a b +. （Ⅰ）求π()4f -的值；（Ⅱ）求()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值和最小值，并求出相应的x 的值. 17. （本小题满分13分）在A B C ∆中，角,,A B C 的对边分别为,,a b c ,且3cos 4B =．（Ⅰ）求2sin sin 22B B +的值；（Ⅱ）若b =ac 取最大值时，求A B C ∆的面积.18.（本小题满分13分）在递增数列}{n a 中，n S 表示数列}{n a 的前n 项和，11a =，1n n a a c +=+（c 为常数，n *∈N ），且123,,a a S 成等比数列. （Ⅰ）求c 的值;（Ⅱ）若12()3nn n b a +=⋅-，*n ∈N ，求242n b b b +++ .19.（本小题满分14分） 设函数221()22xa f x ax -=-+，R a ∈.（Ⅰ）若2]x ∀∈，关于x 的不等式24()2a f x -≥恒成立，试求a 的取值范围；（Ⅱ）若函数()f x 在区间[0,4]上恰有一个零点，试求a 的取值范围.20. （本小题满分14分） 已知函数21()ln (1)2f x x ax a x =-+-（a ∈R 且0a ≠）.（Ⅰ）求函数()f x 的单调区间；（Ⅱ） 记函数()y F x =的图象为曲线C .设点11(,)A x y ,22(,)B x y 是曲线C 上的不同两点，如果在曲线C 上存在点00(,)M x y ，使得：①1202x x x +=；②曲线C 在M 处的切线平行于直线A B ，则称函数()F x 存在“中值相依切线”.试问：函数()f x 是否存在“中值相依切线”，请说明理由.北京市朝阳区2011-2012学年度高三年级第一学期期中统一考试数学试卷（文史类）答案 2011.11注：若有两空，则第一个空第二个空 三、解答题：（15）（本小题满分13分）解：（Ⅰ）当1a =时,不等式化为(2)0x x -<，则{|02}M x x =<<.又{}13N x x =-≤≤，因此{}13M N x x =-≤≤ . ………………6分 （Ⅱ）若1a <-,{|10},M x a x =+<<若M N ⊆,则有110a -≤+<，解得21a -≤<-. ………………8分 若1a =-,,{|13}M N x x φ==-≤≤,此时M N ⊆成立;………………10分若1a >-,{|01},{|13}M x x a N x x =<<+=-≤≤,若M N ⊆,则有013a <+≤, 解得12a -<≤. ………………12分 综上,a 的取值范围是[2,2]-.………………13分（16）（本小题满分13分）解：（Ⅰ）()1f x =⋅+a b =22sin cos 2cos 1x x x -+=sin 2cos 2x x -， …………4分则π()14f -=-. ………………6分（Ⅱ）()f x =sin 2cos 2x x -)4x π-. ………………7分因为π0,2x ⎡⎤∈⎢⎥⎣⎦，所以π3π2,444x π⎡⎤-∈-⎢⎥⎣⎦. ………………9分 则当242x ππ-=时，即8x 3π=时，()f x………………11分当244x ππ-=-时，即0x =时，()f x 的最小值是1-. ………………13分（17）（本小题满分13分） 解：（Ⅰ）因为3cos 4B =，所以sin 4B =………………1分则21sinsin 2(1cos )2sin cos 22B B B B B +=-+=18+3244⨯8.…5分（Ⅱ）由已知得2223cos 24a c bB ac+-==， …………7分又因为b =所以，22332a c ac +-=. …………8分又因为223322a c ac ac +=+≥，所以6a c ≤，当且仅当a c ==ac 取得最大值. …………11分此时11sin 62244ABC S ac B ∆==⨯⨯=所以当ac 取最大值时，A B C ∆4……………13分（18）（本小题满分13分）解：（Ⅰ）11,1,n n a a c a c +=+=为常数， 所以1(1).n a n c =+-则231,1(1)(12)33.a c S c c c =+=++++=+ ………………3分又123,,a a S 成等比数列，所以2(1)33c c +=+，解得1c =-或2c =.由于}{n a 是递增数列，舍去1c =-,故2c =. ………………6分（Ⅱ）由（Ⅰ）得21n a n =-，*n ∈N .所以12()(21)3nn b n =⋅---，2212()(41)3nn b n =⋅---. ……………8分从而 242nb b b +++ 21[1()](341)991219nn n -+-=--211(1)249nn n =---，*n ∈N . ………………13分（19）（本小题满分14分）解：（Ⅰ） 依题得:2]x ∀∈，不等式232x ax +≥恒成立,则322x a x ≤+.…2分设3()22x g x x=+,则min ()a g x ≤即可. ………………3分又3()22x g x x=+≥=，当且仅当x =,min ()g x g ==所以a的取值范围是(-∞. ………………6分 （Ⅱ）二次函数()f x 的图象开口向上，对称轴是直线x a =. ………………7分依题意得：当2a ≤时，只需满足(0)0,(4)0,f f <⎧⎨>⎩即2210,8150,a a a ⎧-<⎨-+>⎩解得11a -<<, ………………10分当1a =-时满足题意，1a =时不满足题意，则11a -≤< . ……………11分当2a >时，只需满足(0)0,(4)0,f f >⎧⎨<⎩即2210,8150,a a a ⎧->⎨-+<⎩解得35a <<. …………12分当5a =时满足题意，3a =时不满足题意，则35a <≤. …………13分 综上所述, a 的取值范围是[1,1)(3,5]- . …………14分 （20）（本小题满分14分）解：(Ⅰ)显然函数()f x 的定义域是(0,)+∞. …………1分由已知得，1(1)()1'()1a x x a f x ax a xx-+=-+-=-. …………2分⑴当0a >时, 令'()0f x >,解得01x <<; 令'()0f x <,解得1x >.所以函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减. …………3分 ⑵当0a <时， ①当11a-<时，即1a <-时, 令'()0f x >,解得10x a<<-或1x >;令'()0f x <,解得11x a-<<.所以，函数()f x 在1(0,)a-和(1,)+∞上单调递增,在1(,1)a-上单调递减;…………4分 ②当11a -=时，即1a =-时, 显然，函数()f x 在(0,)+∞上单调递增； ………5分 ③当11a->时，即10a -<<时, 令'()0f x >,解得01x <<或1x a>-;令'()0f x <,解得11x a<<-.所以，函数()f x 在(0,1)和1(,)a-+∞上单调递增,在1(1,)a-上单调递减.…………6分 综上所述，⑴当0a >时,函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减； ⑵当1a <-时,函数()f x 在1(0,)a-和(1,)+∞上单调递增,在1(,1)a-上单调递减；⑶当1a =-时,函数()f x 在(0,)+∞上单调递增； ⑷当10a -<<时,函数()f x 在(0,1)和1(,)a-+∞上单调递增,在1(1,)a-上单调递减.……………7分 (Ⅱ)假设函数()f x 存在“中值相依切线”.设11(,)A x y ,22(,)B x y 是曲线()y f x =上的不同两点，且120x x <<， 则211111ln (1)2y x ax a x =-+-，222221ln (1)2y x ax a x =-+-.2121AB y y k x x -=-22212121211(ln ln )()(1)()2x x a x x a x x x x ---+--=-211221ln ln 1()(1)2x x a x x a x x -=-++-- …………8分曲线在点00(,)M x y 处的切线斜率0()k f x '=12()2x x f +'=12122(1)2x x a a x x +=-⋅+-+， …………9分依题意得：211221ln ln 1()(1)2x x a x x a x x --++--12122(1)2x x a a x x +=-⋅+-+.化简可得：2121ln ln x x x x --122x x =+，即21lnx x =21212()x x x x -+21212(1)1x x x x -=+. …………11分 设21x t x = (1t >)，上式化为：2(1)4ln 211t t t t -==-++,即4ln 21t t +=+. …………12分令4()ln 1g t t t =++,214'()(1)g t tt =-+=22(1)(1)t t t -+.因为1t >,显然'()0g t >，所以()g t 在(1,)+∞上递增, 显然有()2g t >恒成立. 所以在(1,)+∞内不存在t ,使得4ln 21t t +=+成立.综上所述，假设不成立.所以，函数()f x 不存在“中值相依切线”. ……………14分。

北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷（文史类） 2012.1第一部分（选择题 共40分）注意事项：考生务必将答案答在答题卡上，在试卷上答无效。

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项.1.已知集合2{|3},{|log 1}M x x N x x =<=>，则M N 等于（ ）A ．φB ．}321|{<<x x C ．}30|{<<x xD ．{|23}x x <<2.已知平面向量(3,1)=a ，(,3)x =b ，且a ⊥b ，则实数x 的值为（ ）A ．9-B ．1-C ．1D ．93. 函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x 的图象大致是 （ ）4. 设数列{}n a 是公差不为0的等差数列，11a =且136,,a a a 成等比数列，则{}n a 的前n 项和n S 等于 （ ）A ． 2788n n +B ．2744n n + C ．2324n n+D ．2n n +5.执行如图所示的程序框图，输出的S 值为（ ）A ．1B ．1-C ． 2-D ．06. 函数2()2xf x a x=--的一个零点在区间(1,2)内，则实数a 的取值范围是（ ） A ．(1,3) B ．(1,2) C ．(0,3) D ． (0,2)7.已知函数()sin f x x x =，设()7a f π=，()6b f π=，()3c f π=，则,,a b c 的大小关系是 （ ） A. a b c << B.c a b << C.b a c << D.b c a << 8. 已知集合{(,)|,,}A x y x n y na b n ===+∈Z ,{(,)|,B x y x m ==2312,y m =+m ∈Z }.若存在实数,a b 使得AB ≠∅成立,称点(,)a b 为“￡”点，则“￡”点在平面区域22{(,)|108}C x y x y =+≤内的个数是 ( ) A. 0 B. 1 C. 2 D. 无数个第二部分（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.9. 若变量x ，y 满足约束条件1,,236,x y x x y ≥⎧⎪≥⎨⎪+≤⎩则2z x y =+的最大值为 .10. 已知有若干辆汽车通过某一段公路，从中抽取200辆汽车进行测速分析，其时速的频率分布直方图如图所示，则时速在区间[60,70)上的汽车大约有 辆.11. 某几何体的三视图如图所示，则这个几何体的体积是 .时速（km/h ）01002 003 00440 50 60 70 8012. 设直线10x my --=与圆22(1)(2)4x y -+-=相交于A ，B 两点，且弦AB的长为m 的值是 .13. 某公司购买一批机器投入生产，据市场分析每台机器生产的产品可获得的总利润y （万元）与机器运转时间x （年数，x *∈N ）的关系为21825y x x =-+-.则当每台机器运转 年时，年平均利润最大，最大值是 万元.14. 已知两个正数,a b ,可按规则c ab a b =++扩充为一个新数c ,在,,a b c 三个数中取两个较大的数,按上述规则扩充得到一个新数，依次下去，将每扩充一次得到一个新数称为一次操作.（1）若1,3a b ==,按上述规则操作三次,扩充所得的数是__________；（2）若0p q >>，经过6次操作后扩充所得的数为(1)(1)1m n q p ++-（,m n 为正整数），则,m n 的值分别为______________.三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本题满分13分）在锐角三角形ABC 中，a ，b ，c 分别为内角A ，B ，C所对的边，且满足2sin 0b A -=．（Ⅰ）求角B 的大小；（Ⅱ）若b =2c =，求AB AC 的值．16. （本题满分14分）如图，在四棱锥S ABCD -中，平面SAD ⊥平面ABCD ．四边形ABCD 为正方形，且P 为AD 的中点，Q 为SB 的中点． （Ⅰ）求证：CD ⊥平面SAD ； （Ⅱ）求证：//PQ 平面SCD ；（Ⅲ）若SA SD =，M 为BC 中点，在棱SC 上是否存在点N，使得平面DMN ⊥平面ABCD ，并证明你的结论.17. （本题满分13分） 如图，一个圆形游戏转盘被分成6个均匀的扇形区域．用力旋转MSD BCP Q·转盘，转盘停止转动时，箭头A 所指区域的数字就是每次游戏所得的分数（箭头指向两个区域的边界时重新转动），且箭头A 指向每个区域的可能性都是相等的．在一次家庭抽奖的活动中，要求每个家庭派一位儿童和一位成人先后各转动一次游戏转盘，得分记为(,)a b （假设儿童和成人的得分互不影响，且每个家庭只能参加一次活动）． （Ⅰ）请列出一个家庭得分(,)a b 的所有情况；（Ⅱ）若游戏规定：一个家庭的总得分为参与游戏的两人所得分数之和，且总得分为偶数的家庭可以获得一份奖品．请问一个家庭获奖的概率为多少？18. （本题满分13分）设函数2()ln 2,R 2ax f x a x x a =+-∈. （Ⅰ）当1a =时,试求函数()f x 在区间[1,e]上的最大值; （Ⅱ）当0a ≥时,试求函数()f x 的单调区间. 19. （本题满分13分）已知椭圆2222:1(0)x y C a b a b +=>>的离心率为12，且过点3(1,)2P ，F 为其右焦点.（Ⅰ）求椭圆C 的方程；（Ⅱ）设过点(4,0)A 的直线l 与椭圆相交于M 、N 两点（点M 在,A N 两点之间），若AMF △与MFN △的面积相等，试求直线l 的方程.20. （本题满分14分） 数列{}n a ，{}n b （1,2,3,n =）由下列条件确定：①110,0a b <>；②当2k ≥时，k a 与k b 满足：当011≥+--k k b a 时，1-=k k a a ,211--+=k k k b a b ；当011<+--k k b a 时，211--+=k k k b a a ，1-=k k b b . （Ⅰ）若11a =-，11b =，求2a ，3a ，4a ，并猜想数列}{n a 的通项公式（不需要证明）； （Ⅱ）在数列}{n b 中，若s b b b >>> 21(3s ≥,且*s ∈N )，试用11,b a 表示k b ，},,2,1{s k ∈；（Ⅲ）在（Ⅰ）的条件下，设数列}{n c (*)n ∈N 满足211=c ，0n c ≠，2212m n n n mc c c ma -+=-+(其中m 为给定的不小于2的整数)，求证：当m n ≤时，恒有1<n c .北京市朝阳区2011-2012学年度高三年级第一学期期末统一考试数学试卷（文史类）答案 2012.1二、填空题：注：若有两空，则第一个空第二个空三、解答题：（15）（本小题满分13分）解：2sin 0b A -=，根据正弦定理得：2sin sin 0A B A -=.………………………………………………………3分因为sin 0A ≠，所以23sin =B . ………………………………………………5分 又B 为锐角， 则3B π=. …………………………………………………6分（Ⅱ）由（Ⅰ）可知，3B π=．因为b =2c =，根据余弦定理，得 2744cos3a a π=+-， ……………………………………8分整理，得2230a a --=．由于0a >，得3a =． ……………………………10分于是222cos214b c a A bc +-===， ………………………………11分所以 cos cos 21AB AC AB AC A cb A ====． ……………13分（16）（本小题满分14分）证明：（Ⅰ）因为四边形ABCD 为正方形，则CD AD ⊥. …………………1分 又平面SAD ⊥平面ABCD ， 且面SAD 面ABCD AD =，所以CD ⊥平面SAD . ………………………………………………………3分（Ⅱ）取SC 的中点R ，连QR, DR ．由题意知：PD ∥BC 且PD =12BC ．…………………4分在SBC ∆中，Q 为SB 的中点，R 为SC 的中点， 所以QR ∥BC 且QR =12BC ．所以QR ∥PD 且QR=PD ，则四边形PDRQ 为平行四边形. …………………………………………………7分 所以PQ ∥DR .又PQ ⊄平面SCD ，DR ⊂平面SCD ，所以PQ ∥平面SCD ． ……………………………………………………………10分 （Ⅲ）存在点N 为SC 中点，使得平面DMN ⊥平面ABCD ． ………………11分连接PC DM 、交于点O ，连接PM 、SP ， 因为//PD CM ，并且PD CM =，所以四边形PMCD 为平行四边形，所以PO CO =. 又因为N 为SC 中点，所以//NO SP ．………………………………………………………………………12分 因为平面SAD ⊥平面ABCD ，平面SAD 平面ABCD =AD ，并且SP AD ⊥， 所以SP ⊥平面ABCD ，所以NO ⊥平面ABCD ， ……………………………………………………13分 又因为NO ⊂平面DMN ，所以平面DMN ⊥平面ABCD ．……………………………………………………14分 （17）（本小题满分13分） 解：（Ⅰ）由题意可知，一个家庭的得分情况共有9种，分别为(2,2),(2,3),(2,5),(3,2)，(3,3),(3,5),(5,3),(5,2),(5,5)． …………………………………………………………7分（Ⅱ）记事件A ：一个家庭在游戏中获奖，则符合获奖条件的得分情况包括(2,2)，(3,3),(3,5),(5,3),(5,5)共5种， ……………………………………………11分 所以5()9P A =． 所以一个家庭获奖的概率为59． …………………………………………………13分（18）（本小题满分13分）解: （Ⅰ）函数()f x 的定义域为(0,)+∞. ………………………………………………1分当1a =时,2()ln 22x f x x x =+-，因为21(1)()20x f x x x x -'=+-=≥， …3分 M SDBCAPQ·R (N ) O所以函数()f x 在区间[1,e]上单调递增，则当=e x 时,函数()f x 取得最大值2e (e )12e 2f =+-. …………………………………………………………………5分（Ⅱ）22()ax x af x x-+'=. ………………………………………………………6分当0a =时,因为()20f x '=-<，所以函数()f x 在区间(0,)+∞上单调递减；…7分 当0a >时，⑴当2440a ∆=-≤时，即1a ≥时，()0f x '≥，所以函数()f x 在区间(0,)+∞ 上单调递增； …………………………………………………………9分⑵当2440a ∆=->时，即01a <<时，由()0f x '>解得，0x <<，或x >. …………………………………………10分由()0f x '<x <<； ………………………………11分所以当01a <<时，函数()f x 在区间上单调递增；在11(a a +上单调递减，1()a+∞单调递增. ………13分（19）（本小题满分13分）解：（Ⅰ）因为12c a =，所以2a c =，b =. …………………………………1分 设椭圆方程为2222143x y c c+=，又点3(1,)2P 在椭圆上,所以2213144c c +=，解得21c =， …………………………………………………………………………3分所以椭圆方程为22143x y +=. …………………………………………………………4分 （Ⅱ）易知直线l 的斜率存在,设l 的方程为(4)y k x =-， ……………………………………………………………5分由22(4),1,43y k x x y =-⎧⎪⎨+=⎪⎩消去y 整理，得 2222(34)3264120k x k x k +-+-=， ………………………………………………6分由题意知2222(32)4(34)(6412)0k k k ∆=-+->， 解得1122k -<<. ……………………………………………………………………7分 设11(,)M x y ，22(,)N x y ，则21223234k x x k+=+，⋅⋅⋅⋅⋅⋅ ①， 2122641234k x x k -=+.… ②. 因为AMF △与MFN △的面积相等，所以AM MN =，所以1224x x =+.⋅⋅⋅⋅⋅⋅ ③ ……………………………………10分由①③消去2x 得21241634k x k +=+.⋅⋅⋅⋅⋅⋅ ④将2124x x =-代入②得21126412(24)34k x x k --=+.⋅⋅⋅⋅⋅⋅ ⑤ 将④代入⑤2222224164166412(24)343434k k k k k k ++-⨯-=+++，整理化简得2365k =，解得6k =±，经检验成立. …………………………12分 所以直线l的方程为4)y x =-. …………………………………………13分 （20）（本小题满分14分）（Ⅰ）解：因为011=+b a ，所以112-==a a ,02112=+=b a b . ……1分 因为0122<-=+b a ,则212223-=+=b a a ,320b b ==. ………………2分 333421222a b a a +===-. ……………………………………………………3分 猜想当2n ≥时，22221111222n n n n a a ---⎛⎫⎛⎫=⨯=-⋅=-⎪⎪⎝⎭⎝⎭.则21,1,1, 2.2n n n a n -⎧-=⎪=⎨-≥⎪⎩ …………………………………………………………4分（Ⅱ）解：当s k ≤≤2时，假设110k k a b --+<，根据已知条件则有1-=k k b b ，与s b b b >>> 21矛盾，因此110k k a b --+<不成立， ……………………5分所以有110k k a b --+≥，从而有1k k a a -=，所以1a a k =. ……………………6分当011≥+--k k b a 时，1-=k k a a ，211--+=k k k b a b , 所以111111()22k k k k k k k a b b a a b a -----+-=-=-; …………………………8分当s k ≤≤2时，总有111()2k k k k b a b a ---=-成立. 又110b a -≠，所以}{k k a b -(s k ,,2,1 =)是首项为11b a -，公比为12的等比数列， ……9分 11121)(-⎪⎭⎫⎝⎛-=-k k k a b a b ，1,2,,k s =,又因为1a a k =，所以111121)(a a b b k k +⎪⎭⎫⎝⎛-=-. …………………………10分（Ⅲ）证明：由题意得2212m n n n mc c c ma -+=-+n n c c m+=21. 因为211n n n c c c m +=+，所以2110n n n c c c m+-=>.所以数列{}n c 是单调递增数列. ………………………………………………11分 因此要证)(1m n c n ≤<，只须证1<m c . 由2≥m ，则n n n c c m c +=+211<n n n c c c m ++11，即1111n n c c m+->-. …12分因此1122111)11()11()11(1c c c c c c c c m m m m m +-++-+-=--- m m m m 121+=+-->. 所以11m mc m <<+. 故当m n ≤,恒有1<n c . ………………………………………………………14分。

2012北京市高三一模数学文分类汇编：三角函数【2012年北京市西城区高三一模文】11. 函数22sin 3cos y x x =+的最小正周期为_____． 【答案】π【解析】函数x x y 2cos 2cos 212+=+=，所以周期为ππ=22。

【2012北京市门头沟区一模文】10. 在ABC ∆中，已知2=a ，3=b ，7=c ，则ABC ∆的面积是 ． 【答案】233 【2012北京市门头沟区一模文】已知31)4tan(=-πα，则α2sin 等于(A)32(B)31 (C)54 (D)52 【答案】C【2012北京市海淀区一模文】（10）若tan 2α=，则sin 2α= . 【答案】45【2012北京市房山区一模文】12．已知函数()ϕω+=x x f sin )(（ω>0, 20πϕ<<）的图象如图所示，则ω=____，ϕ=___.【答案】2，3π【2012北京市东城区一模文】（6）已知sin(45)10α-=-，且090<<α，则cos α的值为 （A ）513 （B ）1213 （C ） 35 （D ）45【答案】D【2012北京市朝阳区一模文】9.若sin θ=,(,)2θπ∈π，则tan θ= .【答案】【2012北京市石景山区一模文】3.函数1sin()y x π=+-的图象（ ）【答案】A【解析】函数x x y sin 1)sin(1+=-+=π的图象关于2π=x 对称，选A.【2012北京市石景山区一模文】15．（本小题满分13分）在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ，且C b B c a c o s c o s )2(=-． （Ⅰ）求角B 的大小； （Ⅱ）若2,4==a A π，求ABC ∆的面积.【答案】解：（Ⅰ）∵ C b B c a cos cos )2(=-，由正弦定理，得∴ C B B C A cos sin cos )sin sin 2(=-． …………2分∴ A C B C B B C B A sin )sin(cos sin cos sin cos sin 2=+=+=，………4分 ∵ ()π，0∈A , ∴0sin ≠A ∴ 21cos =B ． 又∵ π<<B 0 ， ∴ 3π=B ． …………6分 （Ⅱ）由正弦定理BbA a sin sin =，得622232=⨯=b …………8分,43A B ππ==426sin +=∴C …………11分 A ．关于2x π=对称 B ．关于y 轴对称 C ．关于原点对称 D ．关于x π=对称2334266221s i n 21+=+⨯⨯⨯==∴C ab s ． …………13分【2012北京市朝阳区一模文】15. （本题满分13分）已知函数π()cos()4f x x =-. （Ⅰ）若3()5f α=，其中π3π,44α<<求πsin 4α⎛⎫- ⎪⎝⎭的值； （II ）设()()2g x f x f x π⎛⎫=⋅+⎪⎝⎭，求函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【答案】解：（Ⅰ）因为π3()cos()45f αα=-=，且ππ042α<-<， …………1分所以π4sin 45α⎛⎫-= ⎪⎝⎭. .…………5分. （II ）()π()2g x f x f x ⎛⎫=⋅+⎪⎝⎭=ππcos()cos()44x x -⋅+=ππsin()cos()44x x +⋅+ =1πsin(2)22x +=1cos 22x . .…….…..10分 当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2,33x ⎡⎤∈-⎢⎥⎣⎦. 则当0x =时，()g x 的最大值为12；当π3x =时，()g x 的最小值为14-. ………13分 【2012北京市门头沟区一模文】15.（本小题满分13分）已知向量)1,(sin -=x a ，)2,cos 3(x b =，函数2)()(b a x f +=． （I ）求函数)(x f 的最小正周期； （II ）若]2,4[ππ-∈x ，求函数)(x f 的值域．【答案】解：（I ）由已知222)21()cos 3(sin )()(+-++=+=x x b a x f ……2分化简，得3)62sin(2)(++=πx x f……4分函数)(x f 的最小正周期ππ==22T……6分（II ）]2,4[ππ-∈x ，则67623πππ≤+≤-x ， ……8分 所以1)62sin(23≤+≤-πx……10分函数)(x f 的值域是]5,33[-……13分【2012年北京市西城区高三一模文】15.（本小题满分13分）在△ABC 中，已知2sin cos sin()B A A C =+． （Ⅰ）求角A ；（Ⅱ）若2BC =，△ABC AB ．【答案】（Ⅰ）解：由πA B C ++=，得sin()sin(π)sin A C B B +=-=． ……3分所以原式化为B A B sin cos sin 2=． …………4分 因为(0,π)B ∈，所以 0sin >B ， 所以 21cos =A ． …………6分 因为(0,π)A ∈， 所以 π3A =． …………7分 （Ⅱ）解：由余弦定理，得 222222cos BC AB AC AB AC A AB AC AB AC =+-⋅⋅=+-⋅．………9分因为 2BC =，1πsin 23AB AC ⋅⋅= 所以 228AB AC +=． …………11分因为 4AB AC ⋅=， 所以 2AB =. ………13分 【2012北京市海淀区一模文】（15）（本小题满分13分）已知函数()sin sin()3f x x x π=+-. （Ⅰ）求()f x 的单调递增区间；（Ⅱ）在ABC ∆中，角A ，B ，C 的对边分别为,,a b c . 已知()f A =a =，试判断ABC ∆的形状.【答案】解：（Ⅰ）()sin sin()3f x x x π=+-1sin sin 2x x x =+- ………………………………………2分3sin 22x x =-1cos 22x x ÷ç÷=-ç÷ç÷)6x π=-. ………………………………………4分 由22,262k x k k πππππ-<-<+?Z ， 得：222,33k x k k ππππ-<<+?Z . 所以 ()f x 的单调递增区间为2(2,2)33k k ππππ-+，k ÎZ . ………………………………………6分（Ⅱ）因为 ()2f A =，所以)6A π-=.所以1sin()62A π-=. ………………………………………7分因为 0A π<<，所以 5666A πππ-<-<. 所以 3A π=. ………………………………………9分因为 sin sin a bA B=，a =， 所以 1sin 2B =. ………………………………………11分因为 a b >，3A π=，所以 6B π=.所以 2C π= .所以 ABC ∆为直角三角形. ………………………………………13分【2012北京市东城区一模文】（15）（本小题共13分） 已知函数22()(sin2cos2)2sin 2f x x x x =+-. （Ⅰ）求()f x 的最小正周期；（Ⅱ）若函数()y g x =的图象是由()y f x =的图象向右平移8π个单位长度得到的，当x ∈[0,4π]时，求()y g x =的最大值和最小值.【答案】解：（Ⅰ）因为22()(sin 2cos2)2sin 2f x x x x =+-sin 4cos 4x x =+)4x π=+ , …………6分所以函数()f x 的最小正周期为2π. …………8分（Ⅱ）依题意,()y g x ==[4()8x π-4π+])4x π=-. …………10分因为04x π≤≤，所以34444x πππ-≤-≤. …………11分 当442x ππ-=，即316x π=时，()g x当444x ππ-=-，即0x =时， ()g x 取最小值1-. …………13分 【2012北京市房山区一模文】15．（本小题共13分）已知ABC △中，内角C B A ,,的对边分别为c b a ,,，且552c o s =A ，10103cos =B ． （Ⅰ）求()B A +cos 的值；（Ⅱ）设10=a ，求ABC △的面积．【答案】解：（Ⅰ）∵C B A ,,为ABC ∆的内角，且，552cos =A ，10103cos =B ∴555521cos 1sin 22=⎪⎪⎭⎫ ⎝⎛--=-=A A1010101031cos 1sin 22=⎪⎪⎭⎫ ⎝⎛-=-=B B ………………………………………4分∴()B A +cos B A B A sin cos cos +=10105510103552⨯-⨯=22=………………………………………7分 （Ⅱ）由（I ）知， 45=+B A∴ 135=C ………………………………………8分 ∵10=a ，由正弦定理BbA a sin sin =得 555101010sin sin =⨯=⨯=A Ba b ……………………………………11分 ∴ABC S ∆252251021sin 21=⨯⨯⨯==C ab ……………………………………13分 【2012北京市丰台区一模文】15．（本小题共13分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin cos cos .a B b C c B -= （I ）判断△ABC 的形状；（Ⅱ）若()sin cos f x x x =+，求f （A ）的最大值．【答案】。

2012北京市高三一模数学文分类汇编:立体几何【2012年北京市西城区高三一模文】5．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（ ）（A ）243cm （B ）223cm （C ）28cm （D ）24cm【答案】A【解析】正六棱柱的左视图是一个以AB 长为宽，高为2的矩形,32=AB所以左视图的面积为34232=⨯,选A 。

【2012北京市门头沟区一模文】己知某几何体的三视图如右图所示,则其体积为(A ） 4(B ） 8 （C)43(D)23【答案】A【2012北京市海淀区一模文】（12已知三条侧棱两两垂直的正三棱锥的俯视图如图所示,那么此三棱锥的体积是，左视图的面积是 . 22俯视图2【答案】23 22【2012北京市房山区一模文】3．一个几何体的三视图如右图所示,则这个几何体的体积为( ）【答案】A【2012北京市东城区一模文】（9）已知一个四棱锥的三视图如图所示，则该四棱锥的体积是 .【答案】43【2012北京市朝阳区一模文】10.已知某几何体的三视图如图所示,则该几何体的体积为 .（A ）32 （B)2 （C)4（D ）5【答案】32【2012北京市朝阳区一模文】5。

关于两条不同的直线m ，n 与两个不同的平面α，β，下列命题正确的是 A ．βα//,//n m 且βα//，则n m // B ．βα⊥⊥n m ,且βα⊥，则m //n C ．βα//,n m ⊥且βα//，则n m ⊥D ．βα⊥n m ,//且βα⊥，则n m //【答案】C【2012北京市丰台区一模文】4．若某空间几何体的三视图如图所示,则该几何体的体积是（ ）A ．202π-B ．2203π-C ．2403π-D ．4403π-【答案】B【2012北京市石景山区一模文】4。

设n m ,是两条不同的直线，γβα,,是三个不同的平面,下列命题正确的是（ ）A ．αα//,//,//n m n m 则若B ．βαγβγα//,,则若⊥⊥C ．n m n m //,//,//则若ααD ．n m n m ⊥⊥则若,//,αα【答案】D【解析】根据线面垂直的性质可知选项D 正确.【2012北京市石景山区一模文】7．某几何体的三视图如图所示，则它的体积是（ )A ．4383+B ．283+C ．2383+D ．323【答案】A【解析】由三视图可知，该组合体下面是边长为2的正方体，上面是底边边长为2，侧高为2的四棱锥。

2012北京市高三一模数学文分类汇编：集合与简易逻辑 【2012年北京市西城区高三一模文】1．已知集合，，那么（ ） （A）（B）（C）（D） 【答案】C 【解析】，所以，选C. 【2012北京市门头沟区一模文】已知集合，那么满足的集合有 (A) 1个(B)2个(C)3个(D)4个 【答案】D 【2012北京市海淀区一模文】（1）已知集合，，那么=（A） （B） （C） （D） 【答案】C 【解析】，所以,答案选C. 【2012北京市房山区一模文】1．设全集集合，则（B）（C）（D）【答案】B 【2012北京市丰台区一模文】1．已知集合，则（ ） A．B． C．D． 【答案】C 【2012北京市石景山区一模文】1．设,，则A．B．C．D． 【答案】B 【解析】,，所以，答案选B. 【2012年北京市西城区高三一模文】7．设等比数列的前项和为．则“”是“”的（ ） （A）充分而不必要条件 （B）必要而不充分条件 （C）充要条件 （D）既不充分又不必要条件 【答案】C 【解析】，若，则，所以。

若，则，所以，即“”是“”的充要条件，选C. 【2012北京市房山区一模文】2．命题，，命题,，则下列命题中真命题是 （ ） （A）（B）（C）（D） 【答案】D 【2012北京市东城区一模文】 (10) 命题“”的否定是 . 【答案】 【2012北京市丰台区一模文】6．若函数则是“函数在R上的单调递减的”（ ） A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件 【答案】A 【2012北京市朝阳区一模文】2. 若集合，，则“”是“”的 A．充分不必要条件 B必要不充分条件 【2012北京市东城区一模文】（2）若集合，，则“”是“”的 （A）充分不必要条件 （B）必要不充分条件 （C）充分必要条件 （D）既不充分也不必要条件 【答案】A 【2012北京市东城区一模文】（20）(本小题共14分) 对于函数，若，则称为的“不动点”；若，则称为的“稳定点”.函数的“不动点”和“稳定点”的集合分别记为和,即, . （Ⅰ）设函数，求集合和； （Ⅱ）求证：； （Ⅲ）设函数，且，求证：. 【答案】（Ⅰ）解：由，得，解得； …………1分 由，得，解得. …………3分 所以集合，. …………4分 （Ⅱ）证明：若，则显然成立； 若,设为中任意一个元素，则有， 所以，故，所以. …………8分 （Ⅲ）证明：由，得方程无实数解， 则. …………10分 当时，二次函数（即）的图象在轴的上方， 所以任意，恒成立， 即对于任意，恒成立， 对于实数，则有成立， 所以对于任意，恒成立，则. …………12分 ②当时，二次函数（即）的图象在轴的下方， 所以任意，恒成立， 即对于任意，恒成立， 对于实数，则有成立， 所以对于任意，恒成立，则. 综上，对于函数，当时，. …14分 【2012北京市海淀区一模文】（20）（本小题分）M，定义函数对于两个集合M，N，定义集合. 已知A={2，4，6，8，10}，B={1，2，4，8，16}. （Ⅰ）写出和的值，并用列举法写出集合； （Ⅱ）用Card(M)表示有限集合M所含元素的个数. （）求证：当取得最小值时， ； （）求的最小值. 【答案】（Ⅰ）解：，，. ………………………………………3分 （Ⅱ）设当取到最小值时，. （）证明：假设，令. 那么 .这与题设矛盾. 所以 ，即当取到最小值时，. ………………………………………7分 （）同（）可得：且. 若存在且，则令. 那么 . 所以 集合中的元素只能来自. 若且，同上分析可知：集合中是否包含元素，的值不变. 综上可知，当为集合{1,6,10,16}的子集与集合{2,4,8}的并集时，取到最小值4. ………………………………………14分。

北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试数学试卷（文史类）2012.11（考试时间120分钟 满分150分）本试卷分为选择题（共 40分）和非选择题（共 110分）两部分第一部分（选择题共40 分）、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出 符合题目要求的一项•x y 20 C .C . 3C . 3In f （a n ）为等差数列，则称函数f （x ）为“保比差数列函数”.现有定义在（0,）上的如1.已知全集U1,2,3,4,5,6 ,集合 A 1,3,51,2 ,则AI (e u B )等于C .2.曲线y 2xX 3在x1处的切线方程为 3.已知平面向量a ,b 满足 |a| 1, |b|2，且（a b)则a 与b 的夹角是4.已知数列a n是各项均为正数的等比数列，若a 2 2, 2a 3 a 4 16，则 a n 等于C . 2n 2n5.已知角 的终边经过点（3a,4a ）（a0），则sin2等于7A .256.在ABC 中, urn uuU 则 PA (PB12B .25M 是BC 的中点，AMuuuPC)的值为C-Huuu 3，点P 在AM 上，且满足AP24 25uuuu2 PM ,A. B. 2C.2D. 47.函数f(x)3,x ,x0,的图象与函数g （x ） In （x 1）的图象的交点个数是8.已知数列a n 是各项均为正数且公比不等于1的等比数列.对于函数y f （x ），若数列第二部分(非选择题 共110分)二、填空题：本大题共 6小题，每小题5分，共30分.把答案填在答题卡上.19. 已知cos( )—,且 为第二象限的角，则 sin =_，tan = _.2 _ —10. 已知集合 A {x R |x 2} , B = x R I 12x 8 ,则 AI B =_. 2 —11. 设S n 为等差数列{a n }的前n 项和，若33 34 4代 37 16，则公差dS 9uur umr12. 在 ABC 中，若BA BC 4 , ABC 的面积为2，则角B _________________ .f(x) 1 f(x) 1,ntf(x)' 13.已知函数y f (x)满足:f(1)=a (0a 1)，且 f (x 1)则2f(x),f(x) 1,f (2)=__ (用a 表示)；右 1f (3)=— f(2)则a .14.已知函数f (x)是定义在 R 上的奇函数, 且在定义域上单调递增 .当x 1a,时，不等式f(x 2a) f (x) 0恒成立，则实数a 的取值范围是 _.三、解答题：本大题共 6小题，共80分.解答应写出文字说明，演算步骤或证明过程 .15. (本小题满分13分)1 设厶ABC 的内角A,B,C 所对的边分别为a,b,c ，已知a 2,b 3,cosC -. 3(I)求厶ABC 的面积； (n)求 sin(C A)的值. 16. (本小题满分13分)设数列a n 的前n 项和为S n ，已知41 , a n 1 3S n 1 , n N •(I)写出a 2,a 3的值，并求出数列 a n 的通项公式; (n)求数列 na n 的前n 项和T n .12① f (x)-,② f (x) x ,x则为“保比差数列函数”的所有序号为A .①②B .③④③ f (x) e x , ④ f (x)、、x ,C .①②④D .②③④yA217. (本小题满分13分)函数f(x) Asin( x )(A 0, 0,| | )部分2图象如图所示.(I)求f (x)的最小正周期及解析式；(n)设g(x) f(x) 2cos2x，求函数g(x)在区间[0, _]上的最大值和最小值.218. (本小题满分14分)2函数f(x) 2ax 4x 3 a, a R.(I)当a 1时，求函数f(x)在1,1上的最大值；(n)如果函数f(x)在区间1,1上存在零点，求a的取值范围.19. (本小题满分14分)设函数f (x) x ae x, a R .(I)求函数f (x)单调区间；(n)若x R , f (x) 0成立，求a的取值范围.20. (本小题满分13分)给定一个n项的实数列曰忌丄,a n(n N )，任意选取一个实数c，变换T(c)将数列a1,a2,L ,a n变换为数列|印c|,| a? c|,L ,|务c|，再将得到的数列继续实施这样的变换，这样的变换可以连续进行多次，并且每次所选择的实数c可以不相同，第k(k N )次变换记为T k(q)，其中C k为第k次变换时选择的实数•如果通过k次变换后，数列中的各项均为0,则称「(G) , T2G)，…，T k(c k)为“ k次归零变换”(I)对数列：124,8,分别写出经变换「(2) , T2(3) , T3⑷后得到的数列；(n)对数列：1,3,5,7，给出一个“ k次归零变换”，其中k 4 ；(川)证明：对任意n项数列，都存在“ n次归零变换”.北京市朝阳区2012-2013学年度第一学期高三年级期中练习15. （本小题满分13分）1解：（I ）在厶ABC 中，因为cosC -3因为a b ，所以A 为锐角，所以 sin (C A) si nCgcosA cosCgsi nA2012.11、选择题（共40二、填空题（共30分）1)三、解答题（共80分） 所以sin C、.1 cos 2C1 (\2 2'2 ..33所以S VABC1 abgsin C1 2 3 $ 丘 2 & 2 3又由正弦定理得,sin C所以sin Aagsin C c 所以 cos A 1 sin 2 A1 (492)211分2、、2 7 1 4.210、2 八. ........................ 13 分3 9 3 9 2716. （本小题满分13分）解：（I）a2 4 , a3 16. .......................................................... 2 分由题意，a n 1 3S n 1，则当n 2 时，a n 3S n 1 1.两式相减，化简得a n 1 4a n（n 2） . ..................................... 4分a2,又因为a11，a24，- 4，印则数列a n是以1为首项，4为公比的等比数列，所以a n 4n 1( n N ) ................................. 6 分2 n 1(n) T n a1 2a2 3a3 L na n 1 2 4 3 4 L n 4 ,4T n 4 1 2 42 3 43L (n 1) 4n 1 n 4n , ........................ 8 分两式相减得，3T n 1 4 42L 4n 1 n 4n 1— n 4n• ...................... 12 分1 4n 1 1化简整理得，T n 4n(—_) _(n N ). ......................................... 13分17.（本小题满分13分）解: （I）由图可得A2, T2—,所以T .所以2. 2 3 62.................. o................. Z k............. 2 分当x —时，f(x)2，可得2si n(2-)2 ,66因为丨丨-，所以-所以f(x)的解析式为f(x) 2si n(2x ) . ....................................... 5分6(n)g(x) f(x) 2cos2x 2sin(2x 6) 2cos2x2sin 2xcos —62cos 2xs in— 2cos 2x6、、3s in2x cos2x2sin(2 x ) . .............................................. 10 分6因为x [0,—]，所以一2x2 6 6 6当2x ，即x 时，g(x)有最大值，最大值为2 ；.......... 12分6 2 3当2x ，即x 0时，g(x)有最小值，最小值为 1 . ....................... 13分6 618. (本小题满分14分)解：(I)当a 1 时，则f (x) 2x2 4x 42( x22x) 4 2(x 1)2 6 .因为x 1,1 ,所以x 1 时，f(x)max f(1) 2 . .................................. 3分(n)当a 0时，f(x) 4x 3 ,显然在1,1上有零点，所以a 0时成立•……4分当a 0时，令16 8a(3 a) 8(a 1)(a 2) 0,解得a 1, a 2. ........................................... 5分(1)当a 1 时，f(x) 2x2 4x 2 2(x 1)2由f(x) 0,得x 1 [ 1,1];1当a 2 时，f(x) 4x24x 1 4(x -)2.1由f (x) 0 ,得x - [ 1,1],所以当a 0, 1, 2时，y f(x)均恰有一个零点在1,1上. ........... 7分(2)当f ( 1)gf (1) (a 7)(a 1) 0 ,即1 a 7时，y f x在1,1上必有零点. ............................ 9分(3)若y f x在1,1上有两个零点，则a 1 或 a 2..................................................... 14 分19. (本小题满分14分)解：(I) f (x) 1 ae x ............................ 1 分ia 0时，f(x)在区间( ,In a)上是增函数，在区间(In a,)上是减函数 ........... Q由(I)可知：当 a 0时， f (x)0不恒成立................ 9 分又因为当a 0时，f (x)在区间(，In a)上是增函数，在区间 (Ina,)上是减函数，所以f (x)在点x In a 处取最大值，且 f( Ina) Ina ae lna Ina . ........................... 11 分令 Ina，得 a -,e故f(x) 0对x R 恒成立时，a 的取值范围是［―,). ................................................... 14分e20. (本小题满分14分) 解：(I )T 1(2) : 1,0,2,6;T 2(3) : 2,3,1,3; T 3 ⑷：2,1,3,1. .......................................... 3 分a 0,a 0,8(a 1)(a2) 0,8(a 1)(a 2) 0,1 1 1,a或 1- 1,••… a ................. 13分f( 1) 0, f( 1) 0,f(1) 0f(1) 0-解得a 7或a2.综上所述，函数 f(x)在区间1,1上存在极值点，实数 a 的取值范围是当a 0时，令f (x) 0,得xIn a ..................... 4分 若x In a 则 f (x) 0 ,从而 f (x)在区间(,In a)上是增函数；若xIn a 则 f (x) 0,从而 f (x)在区间(In a,)上是减函数.综上可知：当a 0时, f (x)在区间(，)上是增函数；当a 0时，f (x) 0 , f (x)在R 上是增函数. 3分（H）方法1: T⑷：3,1,13 T2（2）: 1,1,1,1; T3（1）: 0,0,0,0方法2：T1（2）: 1,1,3,5; T2（2）: 1,1,1,3; T3（2）: 1,1,1,1 ; T^）: 0,0,0,0.（川）记经过T k（c k）变换后，数列为a（k）£,L ,a n k）.1 1取c, -（31 82）,则31（1） aj —|印321，即经T1（q）后，前两项相等；2 2取c抽1）af），则a12） a22） a32） 11 a^ af |，即经T2G）后，前3 项相等;2 2继续做类似的变换，取C k haf1〉a k k J），（k n 1），经T k（cQ后，得到数列的2前k 1项相等.特别地，当k n 1时，各项都相等，最后，取c n aj1〉，经T n（c n）后,数列各项均为0.所以必存在n次“归零变换”.（注：可能存在k次“归零变换”，其中k n）. ...................... 13分。

2012-2013学年北京市朝阳区高三（上）期末数学试卷（文科）一、选择题：本大题共8小题，每小题5分，共40分．1. 设集A={x|0<x<2}，集合B={x|log2x>0}，则A∩B等于（）A.{x|x<2}B.{x|x>0}C.{x|0<x<2}D.{x|1<x<2}2. 设i是虚数单位，复数1+ai2−i为纯虚数，则实数a为（）A.2B.−2C.−12D.123. “k=1”是“直线x−y+k=0与圆x2+y2=1相交”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.即不充分也不必要条件4. 执行如图所示的程序框图．若输入x=3，则输出k的值是（）A.3B.4C.5D.65. 已知x>0，y>0，且2x+y=1，则xy的最大值是（）A.1 4B.18C.4D.86. 已知三棱锥的底面是边长为1的正三角形，其正视图与俯视图如图所示，则其侧视图的面积为（）A.√34B.√32C.34D.17. 已知函数f(x)={e x+a，x≤0,2x−1,x>0(a∈R)，若函数f(x)在R上有两个零点，则a的取值范围是( )A.(−∞, −1)B.(−∞, 0)C.(−1, 0)D.[−1, 0)8. 在棱长为1的正方体ABCD−A1B1C1D1中，点P1，P2分别是线段AB，BD1（不包括端点）上的动点，且线段P1P2平行于平面A1ADD1，则四面体P1P2AB1的体积的最大值是（）A.124B.112C.16D.12二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.已知数列1，a，9是正项等比数列，数列1，b1，b2，9是等差数列，则|a|b1+b2的值为________．在△ABC中，角A、B、C所对的边分别为a、b、c，且b2+c2=a2+bc，则角A的大小为________．在平面直角坐标系中，若不等式组{x+y−1≥0x−1≤0ax−y+1≥0（a为常数）所表示的平面区域内的面积等于2，则a=________．已知双曲线中心在原点，一个焦点为F1(−√5, 0)，点P在双曲线上，且线段PF1的中点坐标为(0, 2)，则此双曲线的方程是________，离心率是________．在直角三角形ABC 中，∠ACB =90∘，AC =BC =2，点P 是斜边AB 上的一个三等分点，则CP →⋅CB →+CP →⋅CA →=________．将连续整数1，2，…，25填入如图所示的5行5列的表格中，使每一行的数字从左到右都成递增数列，则第三列各数之和的最小值为________，最大值为________．三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.已知函数f(x)=sin x2cos x2+cos 2x2−12． （1）求函数f(x)的最小正周期和单调减区间；（2）求函数f(x)在[−π4，π]上最大值和最小值．在长方体ABCD −A 1B 1C 1D 1中，AA 1=AD =2，E 是棱CD 上的一点．（1）求证：AD 1⊥平面A 1B 1D ；（2）求证：B 1E ⊥AD 1；（3）若E 是棱CD 的中点，在棱AA 1上是否存在点P ，使得DP // 平面B 1AE ？若存在，求出线段AP 的长；若不存在，请说明理由．某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为10作为样本进行统计．请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图（如图所示）解决下列问题： 频率分布表（1）写出a ，b ，x ，y 的值；（2）在选取的样本中，从竞赛成绩是80分以上（含8的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动．(ⅰ)求所抽取的2名同学中至少有1名同学来自第5组的概率； (ⅱ)求所抽取的2名同学来自同一组的概率．已知函数f(x)=a(x −1x )−2ln x(a ∈R)．(1)若a =2，求曲线y =f(x)在点（1, f(1)）处的切线方程； (2)求函数f(x)的单调区间．已知直线l:x =my +1(m ∈R)与椭圆C ：x 29+y 2t=1(t >0)相交于E ，F 两点，与x 轴相交于点B ．，且当m =0时，|EF|=83．（1）求椭圆C的方程；（2）设点A的坐标为(−3, 0)，直线AE，AF与直线x=3分别交于M，N两点．试判断以MN为直径的圆是否经过点B？并请说明理由．将正整数1，2，3，4，…，n2(n≥2)任意排成n行n列的数表．对于某一个数表，计算各行和各列中的任意两个数a，b(a>b)的比值ab，称这些比值中的最小值为这个数表的“特征值”．（1）当n=2时，试写出排成的各个数表中所有可能的不同“特征值”；（2）若a ij表示某个n行n列数表中第i行第j列的数(1≤i≤n, 1≤j≤n)，且满足a ij={i+(j−i−1)n,i<ji+(n−i+j−1)n,i≥j请分别写出n=3，4，5时数表的“特征值”，并由此归纳此类数表的“特征值”（不必证明）；（3）对于由正整数1，2，3，4，…，n2排成的n行n列的任意数表，若某行（或列）中，存在两个数属于集合{n2−n+1, n2−n+2, ..., n2}，记其“特征值”为λ，求证：λ≤n+1n．参考答案与试题解析2012-2013学年北京市朝阳区高三（上）期末数学试卷（文科）一、选择题：本大题共8小题，每小题5分，共40分．1.【答案】D【考点】交集及其运算【解析】运用对数函数的单调性化简集合B，然后直接进行交集运算．【解答】解：由A={x|0<x<2}，B={x|log2x>0}={x|x>1}．所以，A∩B={x|0<x<2}∩{x|x>1}={x|1<x<2}．故选D．2.【答案】A【考点】复数的运算【解析】复数的分子、分母同乘分母的共轭复数，化简后它的实部为0，可求实数a的值．【解答】复数1+ai2−i =(1+ai)(2+i)(2−i)(2+i)=2−a+2ai+i5，它是纯虚数，所以a＝2，3.【答案】A【考点】直线与圆的位置关系必要条件、充分条件与充要条件的判断点到直线的距离公式【解析】先看当k=1时，可求得圆心到直线的距离小于半径，可知直线与圆相交，判断出充分性；再看当直线与圆相交时求得圆心到直线的距离小于半径求得k的范围，可知必要性不成立，综合可得答案．【解答】解：当k=1时，圆心到直线的距离d=√2=√22<1，此时直线与圆相交，所以充分性成立．反之，当直线与圆相交时，d=2<1，|k|<√2，不一定k=1，所以必要性不成立．故选A4.【答案】C【考点】程序框图【解析】计算循环中x，与i的值，当x>23时满足判断框的条件，退出循环，输出结果k即可．【解答】解：循环前x=3，k=0，接下来x=8，k=1满足判断框条件，第1次循环，x=8+5=13，k=2，第2次判断后循环，x=13+5=18，k=3，第3次判断并循环x=18+5=23，k=4，第4次判断并循环x=23+5=28，k=5，满足判断框的条件退出循环，输出k=5．故选C．5.【答案】B【考点】基本不等式【解析】利用基本不等式的性质即可得出．【解答】解：∵x>0，y>0，且2x+y=1，∴xy=12×2xy≤12(2x+y2)2=18，当且仅当2x=y>0，2x+y=1，即x=14，y=12时，取等号，此时，xy的最大值是18．故选B．6.【答案】C【考点】简单空间图形的三视图【解析】由题意可知三棱锥是正三棱锥，底面正三角形的高与正视图的投影线平行，如此其正视图中底边是正三棱锥的底面边长，由俯视图知底面是边长是√32的三角形，其高是棱锥的高√3，由此作出其侧视图，求侧视图的面积．【解答】解：由题意，此物体的侧视图如图．根据三视图间的关系可得侧视图中，底边是正三角形的高，底面三角形是边长为1的三角形，所以AB=√32，侧视图的高是棱锥的高：√3，∴S△VAB=12×AB×ℎ=12×√32×√3=34．故选：C．7.【答案】D【考点】根的存在性及根的个数判断【解析】由函数的解析式作出函数的图象，分析可得结果．【解答】解：由解析式可得函数的左半部分为指数函数的一部分，且随着a的变化而上下平移，右半部分为直线的一部分，且是固定的，作图如下：结合图象分析可得，当左半部分的图象介于两红线之间时符合题意，而红线与y轴的交点坐标为a+1，且只需0≤a+1<1，即−1≤a<0即可，故选D.8.【答案】A【考点】棱柱、棱锥、棱台的侧面积和表面积【解析】由题意可得△P1P2B∽△AD1B，设出P1B＝x，则P1P2=√2x，P2到平面AA1B1B的距离为x，求出四面体的体积，通过二次函数的最值，求出四面体的体积的最大值．【解答】由题意在棱长为1的正方体ABCD−A1B1C1D1中，点P1，P2分别是线段AB，BD1（不包括端点）上的动点，且线段P1P2平行于平面A1ADD1，△P1P2B∽△AD1B，设P1B＝x，x∈(0, 1)，则P1P2=√2x，P2到平面AA1B1B的距离为x，所以四面体P1P2AB1的体积为V=13×12×(1−x)×1×x=16(x−x2)，当x=12时，体积取得最大值：124．二、填空题：本大题共6小题，每小题5分，共30分.把答案填在答题卡上.【答案】3【考点】等比数列的通项公式等差数列的通项公式【解析】直接由等比数列和等差数列的性质求出a和b1+b2的值，代入要求的式子即可．【解答】解：已知数列1，a，9是正项等比数列，则有：a2=1×9=9，即得：a=3又1，b1，b2，9是等差数列，那么：b1+b2=1+9=10．∴|a|b1+b2=310．故答案为310．【答案】60∘【考点】余弦定理【解析】直接运用余弦定理，将条件代入公式求出角A的余弦值，再在三角形中求出角A即可．【解答】解：∵b2+c2=a2+bc∴b2+c2−a2=bc∴cos A=b2+c2−a22bc=bc2bc=12即A=60∘，故答案为60∘【答案】3【考点】简单线性规划【解析】先根据约束条件{x+y−1≥0x−1≤0ax−y+1≥0（a为常数），画出可行域，求出可行域顶点的坐标，再利用几何意义求关于面积的等式求出a值即可．【解答】解：当a<0时，不等式组所表示的平面区域，如图中的M，一个无限的角形区域，面积不可能为2，故只能a ≥0，此时不等式组所表示的平面区域如图中的N ，区域为三角形区域， 若这个三角形的面积为2，则AB =4，即点B 的坐标为(1, 4)， 代入y =ax +1得a =3．故答案为：3．【答案】 x 2−y 24=1,√5【考点】双曲线的标准方程 双曲线的特性【解析】设出双曲线的方程，利用中点坐标公式求出p 的坐标，将其坐标代入双曲线的方程，通过a ，b ，c 的关系列出另一个等式，解两个方程得到a ，b 的值．即可求解双曲线方程以及双曲线的离心率． 【解答】解：据已知条件中的焦点坐标判断出焦点在x 轴上，设双曲线的方程为x 2a 2−y 2b 2=1 ∵ 一个焦点为(−√5, 0) ∴ a 2+b 2=5①∵ 线段PF 1的中点坐标为(0, 2)，∴ P 的坐标为(√5, 4)将其代入双曲线的方程得5a 2−16b 2=1 ② 解①②得a 2=1，b 2=4， 所以双曲线的方程为x 2−y 24=1．双曲线的离心率为：e =c a =√5． 故答案为：x 2−y 24=1；√5．【答案】 4【考点】平面向量数量积的运算 【解析】由题意建立直角坐标系，可得CP →及CA →，CB →的坐标，而原式可化为CP →⋅(CB →+CA →)，代入化简可得答案．【解答】解：由题意可建立如图所示的坐标系 可得A(2, 0)B(0, 2)，P(23, 43)或P(43, 23)，故可得CP →=(23, 43)或(43, 23)，CA →=(2, 0)，CB →=(0, 2)， 所以CA →+CB →=(2, 0)+(0, 2)=(2, 2)，故CP →⋅CB →+CP →⋅CA →=CP →⋅(CB →+CA →)=(23, 43)⋅(2, 2)=4或=(43, 23)⋅(2, 2)=4，故答案为：4【答案】 45,85 【考点】 归纳推理数列的函数特性【解析】由已知中每一行的数字从左到右都成递增数列，则第三列各数之和取最小值时，各数组成一个以3为首项，以3为公差的等差数列；第三列各数之和取最大值时，各数组成一个以11为首项，以3为公差的等差数列；进而得到答案． 【解答】解：∵ 每一行的数字从左到右都成递增数列， 则第三列的第一个数字最小为3， 第三列的第二个数字最小为6， 第三列的第三个数字最小为9， 第三列的第四个数字最小为12， 第三列的第五个数字最小为15， 此时个数数字的排列次序如表所示：此时第三列各数之和取最小值：45；则第三列的第一个数字最大为11，第三列的第二个数字最大为14，第三列的第三个数字最大为17，第三列的第四个数字最大为20，第三列的第五个数字最大为23，此时个数数字的排列次序如下图所示：此时第三列各数之和取最小值：85；故答案为：45，85三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 【答案】解：（1）f(x)=12sin x+1+cos x2−12=12(sin x+cos x)=√22sin(x+π4)；∴函数最小正周期为2π根据正弦函数的单调性可知，当2kπ+π2≤x+π4≤2kπ+3π2(k∈Z)时，函数单调减∴2kπ+π4≤x≤2kπ+5π4为函数的单调递减区间．（2）∵−π4≤α≤π即0≤α+π4≤5π4，∴f(x)max=f(π4)=√22，f(x)min=f(π)=−12．【考点】函数y=Asin（ωx+φ）的图象变换【解析】（1）先通过倍角公式和两角和公式对函数进行化简整理得f(x)=√22sin(x+π4)，再根据正弦函数图象的性质可知其最小正周期和单调递减区间．（2）根据正弦函数的单调性进而可得函数f(x)的最大值和最小值．【解答】解：（1）f(x)=12sin x+1+cos x2−12=12(sin x+cos x)=√22sin(x+π4)；∴函数最小正周期为2π根据正弦函数的单调性可知，当2kπ+π2≤x+π4≤2kπ+3π2(k∈Z)时，函数单调减∴2kπ+π4≤x≤2kπ+5π4为函数的单调递减区间．（2）∵−π4≤α≤π即0≤α+π4≤5π4，∴f(x)max=f(π4)=√22，f(x)min=f(π)=−12．【答案】解：（1）证明：在长方体ABCD−A1B1C1D1中，因为A1B1⊥面A1D1DA，所以A1B1⊥AD1．…在矩形A1D1DA中，因为AA1=AD=2，所以AD1⊥A1D．…所以AD1⊥面A1B1D．…（2）证明：因为E∈CD，所以B1E⊂面A1B1CD，由（1）可知，AD1⊥面A1B1CD，…所以B1E⊥AD1．…（3）当点P是棱AA1的中点时，有DP // 平面B1AE．…理由如下：在AB1上取中点M，连接PM1ME．因为P是棱AA1的中点，M是AB1的中点，所以PM // A1B1，且PM=12A1B1．…又DE // A1B1，且DE=12A1B1．所以PM // DE，且PM=DE，所以四边形PMED是平行四边形，所以DP // ME．…又DP⊄面B1AE，ME⊂面B1AE，所以DP // 平面B1AE．…此时，AP=12A1A=1．…【考点】直线与平面垂直的判定直线与平面垂直的性质【解析】（1）要证AD1⊥平面A1B1D，只需证明A1B1⊥AD1，AD1⊥A1D即可．（2）要证B1E⊥AD1，只需证明AD1⊥面A1B1CD即可说明结果．（3）点P是棱AA1的中点，使得DP // 平面B1AE，通过在AB1上取中点M，连接PM1ME．证明PM // A1B1，且PM=12A1B1，然后说明四边形PMED是平行四边形，然后证明DP // 平面B1AE．【解答】解：（1）证明：在长方体ABCD−A1B1C1D1中，因为A1B1⊥面A1D1DA，所以A1B1⊥AD1．…在矩形A1D1DA中，因为AA1=AD=2，所以AD1⊥A1D．…所以AD1⊥面A1B1D．…（2）证明：因为E∈CD，所以B1E⊂面A1B1CD，由（1）可知，AD1⊥面A1B1CD，…所以B1E⊥AD1．…（3）当点P是棱AA1的中点时，有DP // 平面B1AE．…理由如下：在AB1上取中点M，连接PM1ME．因为P是棱AA1的中点，M是AB1的中点，所以PM // A1B1，且PM=12A1B1．…又DE // A1B1，且DE=12A1B1．所以PM // DE，且PM=DE，所以四边形PMED是平行四边形，所以DP // ME．…又DP⊄面B1AE，ME⊂面B1AE，所以DP // 平面B1AE．…此时，AP=12A1A=1．…【答案】由题意可知，a＝16，b＝0.04，x＝0.032，y＝0.004．(ⅰ)由题意可知，第4组共有4人，记为A，B，C，D，第5组共有2人，记为X，Y．从竞赛成绩是80分以上（含8的同学中随机抽取2名同学，有AB，AC，AD，BC，BD，CD，AX，AY，BX，BY，CX，CY，DX，DY，XY，共15种情况．设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E，有AX，AY，BX，BY，CX，CY，DX，DY，XY共9种情况．所以随机抽取的2名同学中至少有1名同学来自第5组的概率是P(E)=915=35．答：随机抽取的2名同学中至少有1名同学来自第5组的概率35．(ⅱ)设“随机抽取的2名同学来自同一组”为事件F，有AB，AC，AD，BC，BD，CD，XY共7种情况．所以P(F)=715．答：随机抽取的2名同学来自同一组的概率是715．【考点】分布和频率分布表频率分布直方图古典概型及其概率计算公式【解析】（1）利用频率分布表和频率分布直方图，由题意能求出a，b，x，y的值．(2)(ⅰ)由题意可知，第4组共有4人，记为A，B，C，D，第5组共有2人，记为X，Y．从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学，有15种情况由此能求出随机抽取的2名同学中至少有1名同学来自第5组的概率．(ⅱ)设“随机抽取的2名同学来自同一组”为事件F，有AB，AC，AD，BC，BD，CD，XY共7种情况，由此能求出随机抽取的2名同学来自同一组的概率．【解答】由题意可知，a＝16，b＝0.04，x＝0.032，y＝0.004．(ⅰ)由题意可知，第4组共有4人，记为A，B，C，D，第5组共有2人，记为X，Y．从竞赛成绩是80分以上（含8的同学中随机抽取2名同学，有AB，AC，AD，BC，BD，CD，AX，AY，BX，BY，CX，CY，DX，DY，XY，共15种情况．设“随机抽取的2名同学中至少有1名同学来自第5组”为事件E，有AX，AY，BX，BY，CX，CY，DX，DY，XY共9种情况．所以随机抽取的2名同学中至少有1名同学来自第5组的概率是P(E)=915=35．答：随机抽取的2名同学中至少有1名同学来自第5组的概率35．(ⅱ)设“随机抽取的2名同学来自同一组”为事件F，有AB，AC，AD，BC，BD，CD，XY共7种情况．所以P(F)=715．答：随机抽取的2名同学来自同一组的概率是715．【答案】解：f′(x)=a(1+1x2)−2x=ax2−2x+ax2，…令ℎ(x)=ax2−2x+a．(1)当a=2时，函数f(x)=2(x−1x)−2ln x，f(1)=0，f′(x)=2(1+1x2)−2x．曲线y=f(x)在点（1, f(1)）处的切线的斜率为f′(1)=2．…从而曲线y=f(x)在点（1, f(1)）处的切线方程为y−0=2(x−1)，即2x−y−2=0．…(2)函数f(x)的定义域为(0, +∞)．设ℎ(x)=ax2−2x+a，(a)当a≤0时，ℎ(x)=ax2−2x+a<0在(0, +∞)上恒成立，则f′(x)<0在(0, +∞)上恒成立，此时f(x)在(0, +∞)上单调递减．…(b)当a>0时，△=4−4a2，(I)若0<a<1，由f′(x)>0，即ℎ(x)>0，得0<x<1−√1−a2a或x>1+√1−a2a；…由f′(x)<0，即ℎ(x)<0，得1−√1−a2a<x<1+√1−a2a．…所以函数f(x)的单调递增区间为(0, 1−√1−a2a)和(1+√1−a2a, +∞)，单调递减区间为(1−√1−a2a, 1+√1−a2a)．…(II)若a≥1，ℎ(x)≥0在(0, +∞)上恒成立，则f′(x)≥0在(0, +∞)上恒成立，此时f(x)在(0, +∞)上单调递增．…【考点】利用导数研究曲线上某点切线方程利用导数研究函数的单调性【解析】(1)将a=2代入，对函数f(x)进行求导得到切线的斜率k=f′(1)，切点为（1, f(1)），根据点斜式即可写出切线方程；(2)由题意知先求函数f(x)的定义域，再由(1)得出的导数，设ℎ(x)=ax2−2x+．下面对a进行分类讨论：①当a≤0时，②当若0<a<1时，③当a≥1时，由此可知f(x)的单调增区间和单调递减区间．【解答】解：f′(x)=a(1+1x2)−2x=ax2−2x+ax2，…令ℎ(x)=ax2−2x+a．(1)当a=2时，函数f(x)=2(x−1x)−2ln x，f(1)=0，f′(x)=2(1+1x2)−2x．曲线y=f(x)在点（1, f(1)）处的切线的斜率为f′(1)=2．…从而曲线y=f(x)在点（1, f(1)）处的切线方程为y−0=2(x−1)，即2x−y−2=0．…(2)函数f(x)的定义域为(0, +∞)．设ℎ(x)=ax2−2x+a，(a)当a≤0时，ℎ(x)=ax2−2x+a<0在(0, +∞)上恒成立，则f′(x)<0在(0, +∞)上恒成立，此时f(x)在(0, +∞)上单调递减．…(b)当a>0时，△=4−4a2，(I)若0<a<1，由f′(x)>0，即ℎ(x)>0，得0<x<1−√1−a2a或x>1+√1−a2a；…由f′(x)<0，即ℎ(x)<0，得1−√1−a2a<x<1+√1−a2a．…所以函数f(x)的单调递增区间为(0, 1−√1−a2a)和(1+√1−a2a, +∞)，单调递减区间为(1−√1−a2a, 1+√1−a2a)．…(II)若a ≥1，ℎ(x)≥0在(0, +∞)上恒成立，则f′(x)≥0在(0, +∞)上恒成立，此时f(x) 在(0, +∞)上单调递增． … 【答案】 解：（1）当m =0时，直线l 的方程为x =1，设点E 在x 轴上方，由{x 29+y 2t=1x =1，解得E(1, 2√2t 3)，F(1, −2√2t 3)．所以|EF|=4√2t3=83，解得t =2．所以椭圆C 的方程为x 29+y 22=1．（2）由{x 29+y 22=1x =my +1，得(2m 2+9)y 2+4my −16=0，显然m ∈R ． 设E(x 1, y 1)，F(x 2, y 2)，则y 1+y 2=−4m 2m 2+9，y 1y 2=−162m 2+9． x 1=my 1+1，x 2=my 2+1． 又直线AE 的方程为y =y 1x 1+3(x +3)，由{y =y 1x 1+3(x +3)x =3，解得M(3, 6y 1x 1+3)，同理得N(3, 6y 2x 2+3)．又B(1, 0)， 所以BM →=(2, 6y 1x 1+3)，BN →=(2, 6y 2x 2+3)，又因为BM →⋅BN →=(2, 6y 1x 1+3)•(2, 6y 2x 2+3)=4+36y 1y 2(x 1+3)(x 2+3)=4+36y 1y 2(my 1+4)(my 2+4)=4(my 1+4)(my 2+4)+36y 1y 2m 2y 1y 2+4m(y 1+y 2)+16=−16(4m 2+36)−16×4m 2+16×4(2m 2+9)−32m 2+16(2m 2+9)=−64m 2−576−64m 2+128m 2+5769=0．所以BM →⊥BN →，所以以MN 为直径的圆过点B ． 【考点】圆锥曲线的综合问题 椭圆的标准方程 【解析】（1）m =0时直线l 的方程与椭圆方程联立解得E ，F 坐标，据|EF|=83得到关于t 的方程，解出即可．（2）由{x 29+y 22=1x =my +1消x 得到关于y 的一元二次方程，设E(x 1, y 1)，F(x 2, y 2)，由韦达定理可用m 表示y 1，y 2，根据已知条件可求出M ，N 坐标，判断以MN 为直径的圆是否经过点B ，只需判断是否有BM →⊥BN →，进而转化为是否有BM →⋅BN →=0，通过计算即可验证．【解答】解：（1）当m =0时，直线l 的方程为x =1，设点E 在x 轴上方，由{x 29+y 2t =1x =1，解得E(1, 2√2t 3)，F(1, −2√2t 3)．所以|EF|=4√2t 3=83，解得t =2．所以椭圆C 的方程为x 29+y 22=1．（2）由{x 29+y 22=1x =my +1，得(2m 2+9)y 2+4my −16=0，显然m ∈R ．设E(x 1, y 1)，F(x 2, y 2)，则y 1+y 2=−4m 2m 2+9，y 1y 2=−162m 2+9． x 1=my 1+1，x 2=my 2+1． 又直线AE 的方程为y =y 1x1+3(x +3)，由{y =y1x 1+3(x +3)x =3，解得M(3, 6y 1x 1+3)， 同理得N(3, 6y 2x2+3)．又B(1, 0)， 所以BM →=(2, 6y 1x 1+3)，BN →=(2, 6y 2x 2+3)，又因为BM →⋅BN →=(2, 6y 1x 1+3)•(2, 6y 2x2+3)=4+36y 1y 2(x 1+3)(x 2+3)=4+36y 1y 2(my 1+4)(my 2+4)=4(my 1+4)(my 2+4)+36y 1y 221212=−16(4m 2+36)−16×4m 2+16×4(2m 2+9)−32m 2+16(2m 2+9)=−64m 2−576−64m 2+128m 2+5769=0．所以BM →⊥BN →，所以以MN 为直径的圆过点B ．【答案】 证明：（1）显然，交换任何两行或两列，特征值不变．可设1在第一行第一列，考虑与1同行或同列的两个数只有三种可能，2，3或2，4或3，4． 得到数表的不同是32或43 …第21页 共22页 ◎ 第22页 共22页（2）当n =3时，数表为此时，数表的“特征值”为 43 …当n =4时，数表为此时，数表的“特征值”为54．…当n =5时，数表为此时，数表的“特征值”为65．… 猜想“特征值”为n+1n．…（3）设a ，b(a >b)为该行（或列）中最大的两个数，则λ≤ab ≤n 2n 2−n+1， 因为n 2n 2−n+1−n+1n =n 3−(n 3+1)n(n 2−n+1)=−1n(n 2−n+1)<0所以n 2n 2−n+1<n+1n，从而λ<n+1n…【考点】 演绎推理 归纳推理 类比推理【解析】（1）可设1在第一行第一列，考虑与1同行或同列的两个数的可能，可得特征值；（2）分别写出当n =3，n =4，n =5时的图表，由特征值的定义可得答案．（3）设a ，b(a >b)为该行（或列）中最大的两个数，易得λ≤ab ≤n 2n −n+1，作差可证n 2n −n+1<n+1n，进而可得答案．【解答】 证明：（1）显然，交换任何两行或两列，特征值不变．可设1在第一行第一列，考虑与1同行或同列的两个数只有三种可能，2，3或2，4或3，4．得到数表的不同是32或43…（2）当n =3时，数表为此时，数表的“特征值”为 43 …当n =4时，数表为此时，数表的“特征值”为54．…当n =5时，数表为此时，数表的“特征值”为65．… 猜想“特征值”为n+1n．…（3）设a ，b(a >b)为该行（或列）中最大的两个数，则λ≤ab ≤n 2n 2−n+1， 因为n 2n 2−n+1−n+1n =n 3−(n 3+1)n(n 2−n+1)=−1n(n 2−n+1)<0所以n 2n 2−n+1<n+1n，从而λ<n+1n…。

（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分)两部分【试题总体说明】本套试卷的题型分布与2011年北京高考题没有区别，延续了北京的8、6、6分布。

6道大题的考点与以往也没有什么不同，分别涉及了解三角形、立体几何、概率、导数、解析几何、集合新题型.所以可见，命题人在命题过程中是有考虑的,在试题整体上，没有过多变化，力求平稳。

1．命题覆盖面广，琐碎知识考察力度加大。

这套前14道小题,几乎没有高中同一章节的内容,考察内容十分分散。

其实，这是新课标的一个重要特点。

新课标的理科教材与原大纲相比，内容有增无减，增加了算法、三视图、积分、几何概型、平面几何、参数方程极坐标等许多内容，而这些内容一定要体现在高考试卷中。

本套试题的小题1,2，3，4,5,6,9,10等试题难度较低，考查学生的基础知识掌握情况。

2.中档题注重综合，难题注重新颖.这次试题中的8、14题都是综合问题,第8题是线性规划与集合综合、第14题是新概念的题目,考察学生综合运用知识的能力，稍有失误就会失分。

这套试卷的小题有很鲜明的特色，活而不难.3.解答题构思巧妙，体现知识的综合性，考查学生的素质和能力.这次解答题的命题点与以往是没有变化的，变化的只是具体的题目。

第17题立体几何,考查探索性问题。

15解三角形和向量结合，试题比单独考查三角函数便增加了难度. 18题的背景较为新颖，需读懂题意，考查基古典概率问题。

第20题，以数列为背景考查学生的综合素质,难度较大。

第一部分(选择题 共40分）注意事项：考生务必将答案答在答题卡上，在试卷上答无效。

一、选择题：本大题共8小题,每小题5分,共40分．在每小题给出的四个选项中,选出符合题目要求的一项。

1。

已知集合2{|3},{|log 1}M x x N x x =<=>,则M N 等于 （ )A ．φB ．}321|{<<x xC ．}30|{<<x xD ．{|23}x x <<【答案】D 【解析】2{|3},{|log 1}{|2}M x x N x x x x MN =<=>=>∴=，{|23}x x <<。