(完整word版)第三章 欧拉图和哈密顿图
- 格式:doc
- 大小:503.50 KB
- 文档页数:16





第三章欧拉图与哈密顿图(七桥问题与一笔画,欧拉图与哈密顿图)教学安排的说明章节题目:§3.1环路;§3.2 欧拉图;§3.3 哈密顿图学时分配:共2课时本章教学目的与要求:认识七桥问题的实质,理解一笔画问题的解决方法,会正确理解关于欧拉图和哈密顿图的判断定理,并进行识别.其它:由于欧拉图与一笔画问题密切相关,因此本章首先从一笔画问题讲起,章节内容与教材有所不同。
课堂教学方案课程名称:§3.1环路;§3.2欧拉图;§3.3哈密顿图授课时数:2学时授课类型:理论课教学方法与手段:讲授法教学目的与要求:认识七桥问题的实质,理解一笔画问题的解决方法,会正确理解关于欧拉图和哈密顿图的判断定理,并进行识别.教学重点、难点:(1)理解环路的概念;(2)掌握欧拉图存在的充分必要条件;(3)理解哈密顿图的一些充分和必要条件;教学内容:看图1,有点像“回”字,能不能从某一点出发,不重复地一笔把它画出来?这就是中国民间古老的一笔画游戏,而这个图形实际上也是来源于生活。
中国古代量米用的“斗”?上下都是四方的,底小口大,从上往下看就是这样的图形。
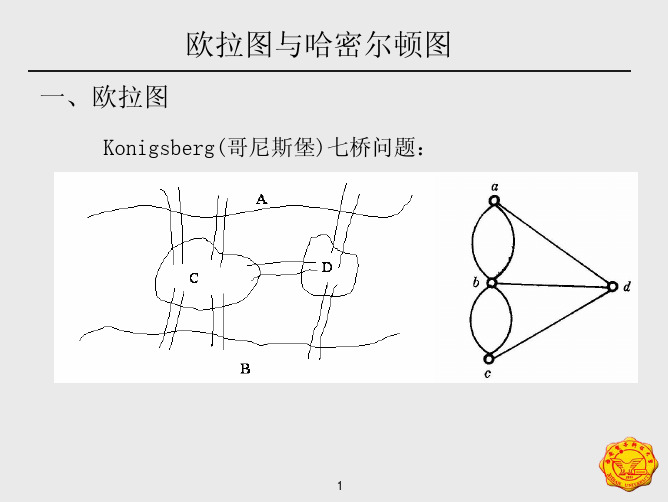
这类“一笔画”问题中最著名的当属“哥尼斯堡七桥问题”了。
一、问题的提出图1哥尼斯堡七桥问题。
18世纪,哥尼斯堡为东普鲁士的首府,有一条横贯全市的普雷格尔河,河中的两个岛与两岸用七座桥联结起来,见图2(1),当时那里的居民热衷于一个难题:游人怎样不重复地走遍七桥,最后回到出发点。
1735年,一群执着好奇的大学生写信请教当时正在圣彼得堡科学院担任教授的著名数学家欧拉。
欧拉通过数学抽象成功地解决了这一问题。
欧拉发现欧几里得几何并不适用于这个问题,因为桥不涉及“大小”,也不能用“量化计算”来解决。
相反地,这问题属于提出的“位置几何”。
欧拉想到,岛与河岸陆地仅是桥梁的连接地点和通往地点,桥仅是从一地通往另一地的路径,一次能否不重复走遍七桥与河岸陆地大小是没有本质联系的,与桥的宽窄也是没有关系的。
第三章欧拉图与哈密顿图(七桥问题与一笔画,欧拉图与哈密顿图)教学安排的说明章节题目:§3.1环路;§3.2 欧拉图;§3.3 哈密顿图学时分配:共2课时本章教学目的与要求:认识七桥问题的实质,理解一笔画问题的解决方法,会正确理解关于欧拉图和哈密顿图的判断定理,并进行识别.其它:由于欧拉图与一笔画问题密切相关,因此本章首先从一笔画问题讲起,章节内容与教材有所不同。
课堂教学方案课程名称:§3.1环路;§3.2欧拉图;§3.3哈密顿图授课时数:2学时授课类型:理论课教学方法与手段:讲授法教学目的与要求:认识七桥问题的实质,理解一笔画问题的解决方法,会正确理解关于欧拉图和哈密顿图的判断定理,并进行识别.教学重点、难点:(1)理解环路的概念;(2)掌握欧拉图存在的充分必要条件;(3)理解哈密顿图的一些充分和必要条件;教学内容:看图1,有点像“回”字,能不能从某一点出发,不重复地一笔把它画出来?这就是中国民间古老的一笔画游戏,而这个图形实际上也是来源于生活。
中国古代量米用的“斗”?上下都是四方的,底小口大,从上往下看就是这样的图形。
这类“一笔画”问题中最著名的当属“哥尼斯堡七桥问题”了。
一、问题的提出图1哥尼斯堡七桥问题。
18世纪,哥尼斯堡为东普鲁士的首府,有一条横贯全市的普雷格尔河,河中的两个岛与两岸用七座桥联结起来,见图2(1),当时那里的居民热衷于一个难题:游人怎样不重复地走遍七桥,最后回到出发点。
1735年,一群执着好奇的大学生写信请教当时正在圣彼得堡科学院担任教授的著名数学家欧拉。
欧拉通过数学抽象成功地解决了这一问题。
欧拉发现欧几里得几何并不适用于这个问题,因为桥不涉及“大小”,也不能用“量化计算”来解决。
相反地,这问题属于提出的“位置几何”。
欧拉想到,岛与河岸陆地仅是桥梁的连接地点和通往地点,桥仅是从一地通往另一地的路径,一次能否不重复走遍七桥与河岸陆地大小是没有本质联系的,与桥的宽窄也是没有关系的。
所以,相对问题而言,可舍弃之,而仅考虑与问题有密切联系的本质特征:岛和岸地可以是仅有位置而没有大小的“点”,桥梁可以是仅有连接作用而没有宽窄的连接两点的线,那么可以把这四处地点用A,B,C,D四个点来表示,同时将七座桥表示成连结其中两点的七条线,就得到这样一张图.于是,欧拉建立了一个数学模型,一个人不重复地走遍所有的七座桥,就相当于从图中某一点出发,不重复地一笔画出图来.这样,“七桥问题”就转化为“一笔画”问题了。
欧拉注意到,如果一个图能一笔画成,那么一定有一个起点开始画,也有一个终点。
图上其它的点是“过路点”——画的时候要经过它。
这些点有什么特征呢?先来看看“过路点”,它应该是“有进有出”的点,有一条边进这点,那么就要有一条边出这点,不可能是有进无出,如果有进无出,它就是终点,也不可能有出无进,如果有出无进,它就是起点。
因此,在“过路点”进出的边总数应该是偶数。
如果起点和终点是同一点,那么它也是属于“有进有出”的点,因此必须连着偶数条边,这样图上所有点都连偶数条边。
如果起点和终点不是同一点,那么这两点连有奇数条边,这也是图中仅有的连着奇数条边的点。
现在对照七桥问题的图,B点连有3条边,A点连有5条边,C点D点各连3条边,哥尼斯堡七桥问题就变成了图2(2)中,是否存在经过每条边一次且仅一次,经过所有的顶点的闭链问题了。
所以欧拉得出的结论是这个图肯定不能一笔画成,也就是说要想不重复的走遍这七座桥是不可能的。
1736年瑞士数学家欧拉(Euler)发表了图论的第一篇论文“哥尼斯堡七桥问题”。
欧拉在论文中指出,这样的闭链是不存在的。
图2欧拉解决问题的关键是两步,先从实际问题中抽象出形式结构,再对形式结构进一步分析,抽象出其本质数量特征,由此得出判别准则,问题获得答案。
哥尼斯堡七桥问题的解决远远超出了它的娱乐价值,欧拉用了最简单的图形——点和线,把一个实际问题抽象成数学问题,巧妙地彻底解决了“七桥问题”。
这充分显示了数学抽象的形式化和量化特征。
由此提出的新思想开辟了数学的一个新的领域——图论,同时也为拓扑学的研究提供了一个初等的例子。
此后许多著名的数学游戏成为图论和拓扑学发展的催化剂和导引,如哈密顿问题(绕行世界问题)、四色猜想等。
直到20世纪中期,这两门学科才逐步完善并迅速发展。
二、欧拉图定义1给定图G=<V,E>,通过G中的每一条边一次且恰好一次的闭链,称为欧拉闭链。
存在欧拉闭链的图称为欧拉图。
欧拉图另一定义:如果图G的所有点均为偶数,则称图G为欧拉图。
实际上,在图中,如果所有的边可以排起来而不重复,则该图为一链,或者是开链,或者是闭链,当是开链时,链中的点为偶数度,起点和终点皆为奇数度。
当是闭链时,链中的点皆为偶数度。
定理1:无向图G为欧拉图当且仅当G连通,并且所有顶点的度都是偶数。
证明:设G为一欧拉图,那么G显然是连通的。
另一方面,由于G本身为一闭路径,它每经过一个顶点一次,便给这一顶点增加度数2,因而各顶点的度均为该路径经历此顶点的次数的两倍,从而均为偶数。
反之,设G连通,且每个顶点的度均为偶数,欲证G为一欧拉图。
为此,对G的边数归纳。
当m = 1时,G必定为顶点的环,如图3(a)所示,显然这时G为欧拉图。
设边数少于m的连通图,在顶点度均为偶数时必为欧拉图,现考虑有m条边的图G。
设想从G的任一点出发,沿着边构画,使笔不离开图且不在构画过的边上重新构画。
由于每个顶点都是偶数度,笔在进入一个顶点后总能离开那个顶点,除非笔回到了起点。
在笔回到起点时,它构画出一条闭路径,记为H。
从图G中删去H的所有边,所得图记为G’,G’未必连通,但其各顶点的度数仍均为偶数(为什么?)。
考虑G的各连通分支,由于它们都连通,顶点度数均为偶数,而边数均小于m,因此据归纳假设,它们都是欧拉图。
此外,由于G连通,它们都与H共有一个或若干个公共顶点(如图3(b)所示),因此,它们与H一起构成一个闭路径。
这就是说,G是一个欧拉图。
(a)图3三、一笔画问题。
要求笔不离纸,而且每条线只画一次,不准重复。
显然哥尼斯堡七桥问题是一笔画问题。
对于图来说,如果全部边(或有向边)可以排成一条链,则称这个图为一个一笔画。
下列图形能否一笔画成?图4定理2设G 是无向连通图,则G 是一笔画⇒G 中只有0或2个奇数度顶点(他们分别是起点和终点)。
即:一笔画0⎧⎨⎩奇数顶点的个数为即全为偶数度,闭链,欧拉图奇数顶点的个数为2开链 证明:设G 的链是点边序列011221k k k v e v e v v e v -,其中顶点可能重复,但边不重复。
对于任一非端点顶点i v ,在欧拉路中每当i v 出现一次,必关联两条边,故i v 虽可重复出现,但是()deg i v 必是偶数。
对于端点,若0k v v =,则()0d e g v 必是偶数,即G 中无奇数度顶点 。
若 0k v v ≠,则()0deg v 必是奇数,()deg k v 必是奇数,即G 中有两个奇数度顶点 。
上述定理的逆定理也成立,即:定理3:设G 是无向连通图, G 中只有0或2个奇数度顶点⇒G 是一笔画。
此定理分两步证:奇数度顶点是0,奇数度顶点是2。
证明思路:只证明奇数度顶点是0 的情形,(证明过程给出了一种构造方法)(1)首先证明任取G 中点0v ,必存在包含0v 的圈。
由于G 中点为偶数度,则从其中一个顶点开始构造一条圈,即从0v 出发经关联边1e 进入1v ,则必可由1v 再经关联边2e 进入2v ,如此下去,每边仅取一次,必存在到达0v 的圈,0112210k k v e v e v v e v -(否则便与G 中点为偶数度矛盾)(2)若P: 0112210k k v e v e v v e v -通过了G 的所有边, P: 0112210k k v e v e v v e v -就是一条闭链。
(3)否则,若G 中去掉P: 0112210k k v e v e v v e v -后得到子图G ',则G '中每个顶点度数都为偶数,因为原来的图G 是连通的,故P: 0112210k k v e v e v v e v -与G '至少有一个顶点i v 重合,在G '中由i v 出发重复(1)的方法,得到闭链L 。
(4)当P 与L 组合,若恰是G ,得欧拉路,否则重复(3),可得闭链M,依此类推可得一条欧拉路。
奇数度顶点是2的情形可类似证明。
因此,定理2与3可总结为设G 是无向连通图, G 中只有0或2个奇数度顶点⇔G 是一笔画。
例1:下列图5中各图是否可以一笔画出?图5解:(1)有 个奇度顶点,无欧拉闭链或通路,不能一笔画成。
(2)与(3)都是个奇度顶点,其余均为偶度顶点,具有欧拉通路,可一笔画成。
(4)均为偶度顶点,具有欧拉通路,可一笔画成。
例2、“两只蚂蚁比赛问题”。
两只蚂蚁甲、乙分别处在图 6左图中的顶点 处,并设图中各边长度相等。
甲提出同乙比赛:从它们所在顶点出发,走过图中所有边最后到达顶点处。
如果它们速度相同,问谁最先到达目的地?解:图 中,有两个奇度顶点 ,因此存在从 到 的开链,蚂蚁乙走到只要走一条欧拉通路,边数为,而蚂蚁甲要想走完图中所有边到达 ,至少要先一条边到达 ,再走一条欧拉通路,故它至少要走 条边到达 ,所以乙必胜。
例3:甲乙两个邮递员去送信,两人以同样的速度走遍所有的街道,甲从A点出发,乙从B点出发,最后都回到邮局(C点)。
如果要选择最短的线路,谁先回到邮局?图中A,C为奇点,其余都是偶点。
甲从A点出发,可以不重复到达C点。
乙从B出发一定会走重复的路,所以甲先回到邮局。
例4图6右图是一个公园的平面图,能不能使游人走遍每一条路不重复?入口和出口又应设在哪儿?H点和B点是奇点,其余都是偶点,所以入后和出口应设在H点和B点。
图6四、中国邮递员问题一名邮递员带着要分发的邮件从邮局出发,经过要分发的每个街道,送完邮件后又返回邮局.如果他必须至少一次走过他管辖范围内的每一条街道,如何选择投递路线,使邮递员走尽可能少的路程.这个问题是由我国数学家管梅谷先生(山东师范大学数学系教授)在1962年首次提出的,因此在国际上称之为中国邮递员问题.用图论的述语,在一个连通的赋权图G(V,E)中,要寻找一条闭链,使该闭链包含G中的每条边至少一次,且该闭链的权数最小.也就是说要从包含G的每条边的闭链中找一条权数最小的闭链.如果G是欧拉图,则很容易由弗罗莱算法求出一个欧拉闭链,但是若G不是欧拉图,即存在奇度数的顶点,则中国由递员问题的解决要困难得多.本节的主要目标是给出在有奇度数顶点的连通图中寻找最小权数的闭链的方法.首先注意到,若图G有奇数度顶点,则G的奇数度顶点必是偶数个.把奇数度顶点分为若干对,每对顶点之间在G中有相应的最短路,将这些最短路画在一起构成一个附加的边子集E .令G/=G+E/,即把附加边子集E/叠加在原图G上形成一个多重图G/,这时G/中连接两个顶点之间的边不止一条.显然G/是一个欧拉图,因而可以求出G /的欧拉闭链.该欧拉闭链不仅通过原图G 中每条边,同时还通过E / 中的每条边,且均仅一次.邮递员问题的难点在于当G 的奇数度顶点较多时,可能有很多种配对方法,应怎样选择配对,能使相应的附加边子集E / 的权数ω(E / )为最小?为此有下列定理.定理 4 设G (V ,E )为一个连通的赋权图,则使附加边子集E / 的权数ω(E / )为最小的充分必要条件是G+E / 中任意边至多重复一次,且G+E / 中的任意闭链中重复边的权数之和不大于该闭链总权数的一半.证明: 必要性.用反证法.设存在一种奇顶点集的配对,使其附加边子集E / 权数 ω(E / )为最小.若 G+E / 中有一条边重复n n () 2次,由于G+E /为欧拉图,所以删去相应的二次重复边后仍为欧拉图.这样,相应的附加边子集的权数将减小,这与 ω(E /)为最小的假设矛盾.这说明E /中的边均互不相同.其次,若G+E / 中存在一个闭链,使它的重复边的权数之和大于该闭链总权数的一半,则在E / 中删去这些重复边(注意:这些边均在E /中),而代之以该闭链的其余部分的边再重复一次.经过这种替代后所得到的边子集E //仍为附加子集,且ω(E //)<ω(E /),又产生矛盾.充分性.设有两个附加边子集E /和E //,均使G+E /和G+E //中每条边至多重复一次,且每个闭链中的重复边的权数和不大该闭链权数的一半,我们来证明ω(E /)=ω(E //).首先注意到,由E /和E //不相同的部分组成的图(记为]\[//////)(E E E E G )是由一个或若干个欧拉子图所组成的.这是因为E /+E //中每个顶点的度数均为偶数,而E /和E //的公共边数也是偶数,故]\[//////)(E E E E G 中每个顶点的度数仍为偶数,所以它若为连通图时是一个欧拉图;若为非连通图时则由若干个欧拉子图组成.]\[//////)(E E E E G 的任何闭链都由E /和E //中的边组成,而E /和E //在闭链中的权数分别不大于该闭链权数的一半,因而任何闭链中属于E /中的权数之和与属于E //中的边数之和必定相等,所以ω(E /)=ω(E //).它就是最优附加边子集的权数,即E /和E //均为使附加边子集的权数达到最小的最优附加边子集.由定理4可得一个寻找邮递员问题最优解的方法.现举例如下:例5已知邮递员要投递的街道如图7左图所示,试求最优邮路.图7解 先找出奇顶点:A 1,A 2,A 3,A 4,B 1,B 2,B 3,B 4.奇顶点进行配对,不妨把A 1与B 1,A 2与B 2,A 3与B 3,A 4与B 4配对,求其最短路.显然它不是最优解.下面我们根据定理4来进行调解.第一次调整:删去多于一条的重复边,即A 3与B 3,A 4与B 4中的(A 4,B 3).调整后,实际上成为A 1与B 1,A 2与B 2,A 3与A 4,B 3与B 4的配对,它们的最短路如图7右图所示.第二次调整:发现在闭链{A 1,A 2,B 2,A 4,B 3,B 4,B 1,A 1}中重复边的权数和为11,大于该闭链权数20的一半.因而调整时,把该闭链的重复边删去,代之以重复其余部分,得图8左图.可以看出,实际上是调整为A 1与A 2,B 1与B 4,A 3与A 4,B 2与B 3配对图8. 第三次调整:在图8左图中发现闭链{ A 3,A 4,B 2,A 3}中重复边的权数和为7,大于该闭链权数10的一半,因而删去原重复边(A 3,V 2,A 4)和(A 4,B 2),而添加(B 2,A 3),得到图8右图.进行检查发现,既没有多于一条的重复边,也没有任何闭链使其重复边的权数之和大于该闭链的一半,因此图8右图就是最优的附加边子集E /,而G+E /为欧拉图,可由弗罗莱算法找出最优邮路.在现实生活中,很多问题都可以转化为中国邮递员问题,例如道路清扫时如何使开空车的总时间最少的问题等等.上面例1题所用的求最优邮路的方法叫“奇偶点图上作业法”.因为此方法要验证每个闭链,很不方便,Edmods和Johnson在1973年提出一种比较有效的方法,有兴趣的读者可参考有关资料.例11.24中国邮路问题中国邮路问题是我国数学家管梅谷先生在20世纪60年代提出来的。