2019全国MBA联考综合能力真题及答案

2019年全国硕士研究生入学统一考试管理类联考综合能力（199）真题一、问题求解：第1—15小题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E 五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1、某车间计划10天完成一项任务，工作了3天后因故停工2天，若要按原计划完成任务，则工作效率需要提高（ ）A.20%B.30%C.40%D.50%E.60% 2、设函数2()2af x x x=+（a ＞0）在（0，+∞）内的最小值为0()12f x =，则x 0=（ ）。

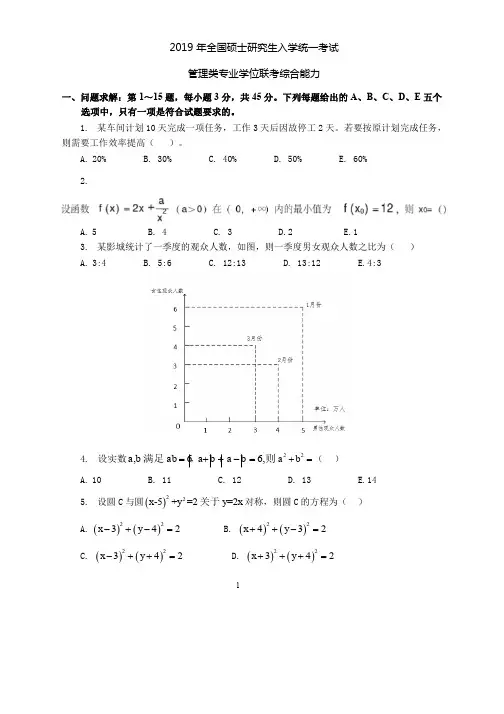
A.5B.4C.3D.2E.13、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数之比为（ ）。

A.3:4B.5:6C.12:13D.13:12E.4:34、设实数a ，b 满足ab =6，6a b a b ++-=，则22a b += A.10 B.11 C.12 D.13 E.145、设圆C 与圆22(5)2x y -+=关于直线y =2x 对称，则圆C 的方程为（ ）。

1女性观众人数A.22(3)(4)2x y -+-=B. 22(4)(3)2x y ++-=C.22(3)(4)2x y -++=D.22(3)(4)2x y +++=E.22(3)(4)2x y ++-=6、在分别记了数字1、2、3、4、5、6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为（ ）。

A.1160 B.1360 C.4360D.4760E.4960 7、将一批树苗种在一个正方形花园的边上，四角都种，如果每隔3米种一颗，那么剩余10颗树苗，如果每隔2米种一颗那么恰好种满正方形的3边，则这批树苗有（ ）。

A.54颗B.60颗C.70颗D.82颗E.94颗 8、10名同学的语文和数学的成绩如表：语文和数学成绩的均值分别为E 1和E 2，标准差分别为σ1和σ2，则（ ）。

2019 年全国硕士研究生入学统一考试管理类专业学位联考综合能力一、问题求解：第1～15 题，每小题3 分，共45 分。

下列每题给出的A、B、C、D、E 五个选项中，只有一项是符合试题要求的。

1. 某车间计划10 天完成一项任务，工作3 天后因故停工2 天。

若要按原计划完成任务，则需要工作效率提高（）。

A. 20%B. 30%C. 40%D. 50%E. 60%2.A. 5B. 4C. 3D.2E.13. 某影城统计了一季度的观众人数，如图，则一季度男女观众人数之比为（）A. 3:4B. 5:6C. 12:13D. 13:12E.4:34. 设实数a,b满足ab = 6，a+ b + a - b = 6,则a2 + b2 = （）A. 10B. 11C. 12D. 13E.145. 设圆C 与圆(x-5)2+y2=2关于y=2x对称，则圆C 的方程为（）A. (x-3)2+(y-4)2=2 C. (x-3)2+(y+4)2=2B. (x+4)2+(y-3)2=2 D. (x+3)2+(y+4)2=212E. ( x + 3)2 + ( y - 4)2= 26. 将一批树苗种在一个正方形花园边上，四角都种，如果每隔 3 米种一棵，那么剩下 10 棵树苗；如果每隔 2 米种一棵，那么恰好种满正方形的 3 条边，则这批树苗有（）棵。

A. 54B. 60C. 70D. 82E. 947. 有分别标记 1,2,3,4,5,6 的 6 张卡片，甲抽取 1 张，乙从余下的卡片中再抽取 2 张， 乙的卡片数字之和大于甲的卡片数字的概率为（）A. 11 60B. 13 60C. 43 60D. 4760E. 49 608. 10 名同学的语文和数学成绩如下：语文和数学的均值分别是 E 1和E 2 ，标准差分别为σ1和σ 2 ，则（ ）A. E 1 > E 2 ,σ1 > σ2B. E 1 > E 2 ,σ1 < σ2C. E 1 > E 2 ,σ1 = σ2D. E 1 < E 2 ,σ1 > σ2E. E 1 < E 2 ,σ1 < σ29. 如图，正方体位于半径为 3 的球内，且一面位于球的大圆上，则正方体表面积最大为 （ ）A. 12B. 18C. 24D. 30E. 3610. 在三角形 ABC 中， AB = 4, AC = 6, BC = 8, D 为BC 中点，则AD =（ ）C. 3D.311. 某单位要铺设草坪，若甲乙两公司合作需要 6 天完成，工时费共 2.4 万元。

下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．
第14题
某中学的5个学科各推荐2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方案有______
A.20种
B.24种
C.30种
D.40种
E.45种
上一题下一题
(15/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．
第15题
设数列{an}满足a1=0，an+1-2an=1，则a100=______
A.299-1
B.299
C.299+1
D.2100-1
E.2100+1
上一题下一题
(16~25/共10题)二、条件充分性判断
要求判断每题给出的条件(1)和(2)能否充分支持题干所陈述的结论．A、B、C、D、E五个选项为判断结果，请选择一项符合试题要求的判断．
A.条件(1)充分，但条件(2)不充分。B.条件(2)充分，但条件(1)不充分。C.条件(1)和条件(2)单独都不充分，但条件(1)和条件(2)联合起来充分。D.条件(1)充分，条件(2)也充分。E.条件(1)和条件(2)单独都不充分，条件(1)和条件(2)联合起来也不充分。
第16题
甲、乙、丙三人各自拥有不超过10本图书，甲再购入2本图书后，他们拥有图书的数量能构成等比数列。则能确定甲拥有图书的数量。
C.(x-3)2+(y+4)2=2
D.(x+3)2+(y+4)2=2
E.(x+3)2+(y-4)2=2
上一题下一题
(6/15)一、问题求解
下列每题给出的A、B、C、D、E五个选项中，只有一个选项符合试题要求．

2019年全国硕士研究生入学统一考试管理类专业学位联考综合能力试题说明：由于2019年试题为一题多卷，因此现场试卷中的选择题部分，不同考生有不同顺序。

请在核对答案时注意题目和选项的具体内容。

一、问题求解（第1～15小题，每小题3分，共45分，下列每题给出的A 、B 、C 、D 、E 五个选项中，只有一个是符合试题要求的，请在答题卡上将所选项的字母涂黑）。

1.某工厂生产一批零件，计划10天完成任务，实际提前两天完成，则每天的产量比计划平均提高了（ ）。

A.15%B.20%C.25%D.30%E.35%2.甲乙两人同时从A 地出发，沿400米跑道同向匀速行走，25分钟后乙比甲少走了一圈。

若乙行走一圈需要8分钟，则甲的速度是（ ）米/分钟A.62B.65C.66D.67E.693.甲班共有30名学生，在一次满分为100分的考试中，全班平均成绩为90分，则成绩低于60分的学生至多有（ ）个。

A.8B.7C.6D.5E.44.某工程由甲公司承包需60天完成，由甲、乙两公司共同承包需28天完成，由乙、丙两公司共同承包需35天完成，则由丙公司承包并完成该工程需要的天数是（ ）A.85B.90C.95D.100E.105 5.已知)10)(9(1)3)(2(1)2)(1(1)(+++⋅⋅⋅++++++=x x x x x x x f ，则=)8(f （ ） A.91 B.101 C.161 D.171 E.181 6.甲乙两商店同时购进了某品牌电视机，当甲商店售出了15台时乙商店售出了10台，此时两店的库存比为8:7，库存差为5，则甲乙两店总进货量为（ ）A.75B.80C.85D.100E.1257.如图，在直角三角形ABC 中，4=AC ，3=BC ，BC DE //，已知梯形BCDE 的面积为3，则=DE （ ） A.3 B.13+ C.434- D.223 E.12+8.点)4,0(关于关于直线012=++y x 的对称点为（ ）A.)0,2(B.)0,3(-C.)1,6(-D.)2,4(E.)2,4(- 9.在52)53(++x x 的展开式中，2x 的系数为（ ）A.5B.10C.45D.90E.9510.有一批水果要装箱，一名熟练工单独装箱需要10天，每天报酬为200元；一名普通工单独装箱需要15天，每天报酬为120元。

2019年管理类MBA 综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出的A 、B 、C 、D 、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1. 某车间计划10天完成一项任务，工作了3天后因故停工2天，若要按原计划完成任务，则工作效率需要提高（ ）.A ．20% B. 30% C. 40% D. 50% E. 60%解析：（C ）解法1：将整个任务的工作量看作单位“1”，则原计划的工作效率为110.工作3天后因故停工2天，余下的工作量为17131010-⨯=，需要5天完成，则工作效率为7751050÷=，工作效率提高了71501040%10-=.解法2：工作3天后因故停工2天,若要按原计划完成任务，就要在剩余的5天内完成原计划7天的工作量，则工作效率需要提高11757100%1100%40%157⎛⎫- ⎪⎛⎫⨯=-⨯= ⎪ ⎪⎝⎭ ⎪⎝⎭。

2. 设函数2()2(0)af x x a x=+>在(0,)+∞内的最小值为0()12f x =，则0x =( ).A. 5B. 4C. 3D. 2E. 1解析：（B ）利用三个数的均值定理求最值：a b c ++≥，且“=”只在a b c ==时取到。

322()231264a a f x x x x x x a a x x =+=++≥==⇒=， 此时有2644x x x x==⇒= 注：本解法中2x 一定要拆成两个相等的数相加，即x x +，如果拆成其它形式(如0.5 1.5x x +)，则不等式取等号的条件就不满足了。

3. 某影城统计了一季度的观众人数，如图，则一季度的男性观众人数与女性观众之比为( ) A. 3:4 B. 5:6 C. 12:13 D. 13:12 E. 4:3 解析：（C ）由图可得一季度男女观众人数分别为：男：54312++=万人； 女：63413++=万人因此一季度男女人数比为：12:134. 设实数,a b 满足6,6ab a b a b =++-=，则22a b +=( ). A. 10 B. 11 C. 12 D. 13 E. 14解析：（D ）解法1：想办法去掉绝对值，由60ab =>知,a b 同号，若同正，不妨设0a b >>，此时263a b a b a b a b a a ++-=++-==⇒=，进而62b a==，代入得2213a b +=；若同负，不妨设0a b <<，此时263a b a b a b a b a a ++-=---+=-=⇒=-，进而62b a==-，代入得2213a b +=。

语文成绩: 90、92、94、88、86、85、87、89、91、93
数学成绩: 94、88、96、93、90、85、84、80、82、98
语文和数学成绩的均値分别为 E1 和 E2,柝准差分别为&1 和&2，则
>E2, &1>&2 >E2, &1<&2
>E2, &1=&2
<E2, &1>&2 <E2, &1<&28
E. 14 [参考答案]D [解析] : ab=6,特值法 a=2，b=3 満足条件，a2+b2=4+9=13，选 D。 5、设圆 C 与圆(x-5)2+y2=2，关于 y=2x 时称，则圆 C 方程为( ) A. (x-3)2+(y-4)2=2 B.(x+4)2+(y-3)2=2 B. (x-3)2+(y+4)2=2 D.(x+3)2+(y+4)2=2 E. (x+3)2+(y-4)2= 2 [参考答案]E 6、将一批树苗种在应该正方形花园边上，四角都种，如果每隔 3 米种一棵，那么剩下 10 课树苗,如果每隔 2 米种一棵那么种满正方形的 3 条边,则这批树苗有( ) 棵 A、54B、60 C、70D、82 E、94 [参考答案]D [详解]设正方形的边长为 x，由已知可得方程 4x/3+10=3x/2+1，求解得 x=54 故树苗有(54x4)/3+10=82，选 D。
2、函数 f(x)=2x+a/π2(a﹥0)，在(0，+∞)内最小值为 f(x )=12，则 x =

MBA联考综合能力真题2019年2. 设函数在(0，+∞)内的最小值为f(x0)=12，则x0=______ •B[解析] 本题考查均值不等式。

由于x＞0，a＞0，则f(x)的表达式各项均大于0，考虑运用均值不等式分析其最小值。

则a=64，当且仅当，即x=4时取等号。

故本题选B。

•方法二(计算法)：两圆圆心关于直线y=2x 对称，即两点连线的中点在y=2x 上，两点连线与y=2x垂直。

设圆C 的圆心为(a ，b)，则满足方程组解得即圆C 的圆心为(-3，4)，半径与已知圆半径相等，所以圆C 的方程为(x+3)2+(y-4)=2。

故本题选E 。

6. 将一批树苗种在一个正方形花园的边上，四角都种。

如果每隔3米种一棵，那么剩余10棵树苗；如果每隔2米种一棵，那么恰好种满整个正方形的3条边，则这批树苗有______D[解析] 本题考查植树问题。

设正方形边长为x，四个角都种树且每隔3米种一棵树，四边种满，则所种树总数为；四个角都种树且每隔2米种一棵树，种满三边，则所种树总数为。

根据题意有，得x=54。

这批树苗共有棵。

故本题选D。

注：在封闭路线上植树，植树总棵数=距离÷间距。

在非封闭路线上植树，若两端都植树，植树总棵数=距离÷间距+1。

7. 在分别标记了数字1，2，3，4，5，6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为______A．B．C．D．E．D[解析] 本题考查古典概型。

甲先抽取到每一个数字的概率均为。

乙从剩下的卡片中抽取两张，不同的情况总数均为，其中有一些情况不满足大于甲所抽取的卡片数字。

如下表：所求事件概率为。

故本题选D。

B[解析] 本题考查均值与方差。

语文成绩从小到大排序，86，87，88，89，90，91，92，93，94，95，为连续自然数，均值；数学成绩从小到大排序，80，82，84，85，88，90，93，94，96，98，前后对应位置两个数之和都相等，均值。

全国硕士研究生入学统一考试管理类联考综合能力（199）真题一、问题求解：第1—15小题,每小题3分,共45分. 下列每题给出的A、B、C、D、E五个选项中, 只有一项是符合试题要求的. 请在答题卡上将所选项的字母涂黑.1.某品牌的电冰箱连续两次降价10%后的售价是降价前的（）。

（A）80%（B）81%（C）82%（D）83%（E）85%2.张老师到一所中学进行招生咨询，上午接受了45名同学的咨询，其中的9人下午又咨询了张老师，占他下午咨询学生的10%，一天张老师咨询的学生人数为（）。

（A）81（B）90（C）115（D）126（E）1351（A4. x（A5.（A6.（A7.备，则购买的甲、乙办公设备的件数分别为（ ）。

（A ）3，5 （B ）5，3 （C ）4，4 （D ）2，6 （E ）6，28.老师问班上50名同学周末复习的情况，结果有20人复习过数学，30人复习过语文，6人复习过英语，且同时复习了数学和语文的有10人，语文和英语的有2人，英语和数学的有3人，若同时复习过这三门课的人数为0，则没复习过这三门课程的学生人数为（ ）。

（A ）7 （B ）8 （C ）9 （D ）10 （E ）119.如图1，在扇形AOB 中，π∠⊥ＡＯＢ＝，ＯＡ＝１，ＡＣＯＢ，４则阴影部分的面积为（ ）。

（A ）1π－８４ （B ）1π－８８ （C ）1π－４２ （D ）1π－４４ （E ）1π－４８ 1和100之间，能被9整除的正数的平均值是（ ）。

27（B ）36（C ）45（D ）54（E ）63已知ABC ∆和A B C '''∆满足:'''''∠∠πＡＢ：ＡＢ＝ＡＣ：ＡＣ＝２３，Ａ＋Ａ＝，ABC 与A B C '''∆的面积之比为（ ）。

（A ）２：３ （B ）３：５ （C ）２:３ （D ）:２５（E ）４:９ 12.甲从1，2，3中抽取一数，记为a ，乙从1，2，3，4中抽取一数，记为b,规定当ａ＞ｂ或ａ＋１＜ｂ时甲获胜，则甲获胜的概率为（ ）。

2019考研管理类联考综合能力真题一、问题求解（本大题共15小题，每小题3分，共45分）下列每题给出5个选项中，只有一个是符合要求的，请在答题卡上将所选择的字母涂黑。

1.某车间计划10天完成一项任务，工作3天后因故停工2天，若仍要按原计划完成任务，则工作效率需提高（）A.20% B.30% C.40% D.50% E.60%2.设函数()()==+∞>+=002,12,0)0(2)(x x f a xax x f 则内的最小值在（）A.5B.4C.3D.2E.13.某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数之比为().A.3:4B.5:6C.12:13D.13:12E.4:34.设实数b a ,满足=+=-++=22,6,6b a b a b a ab 则().A.10B.11C.12D.13E.145.()C x y y x C 对称，则圆关于直线与圆设圆22522==+-的方程为().A.()()24322=-+-y x B.()()23422=-++y x C.()()24322=++-y x D.()()24322=+++y x E.()()24322=-++y x 6.在分别标记了数字1、2、3、4、5、6的6张卡片中，甲随机抽取1张后，乙从余下的卡片中再随机抽取2张，乙的卡片数字之和大于甲的卡片数字的概率为().A.6011 B.6013 C.6043 D.6047 E.60497.将一批树苗种在一个正方形花园的边上，四角都种，如果每隔3米种一棵，那么剩余10棵树苗，如果每隔2米种一棵那么恰好种满正方形的3条边，则这批树苗有().A.54棵 B.60棵 C.70棵 D.82棵 E.94棵8.10名同学的语文和数学的成绩如表：语文成绩90929488869587899193数学成绩94889693908584808298语文和数学成绩的均值分别为，则和，标准差分别为和2121σσE E ().A.2121σσ>>，E EB.2121σσ<>，E EC.2121σσ=>，E E D.2121σσ><，E E E.2121σσ<<，E E 9.如图，正方体位于半径为3的球内，且其中一面位于球的大圆上，则正方体表面积最大为().A.12B.18C.24D.30E.3610.在三角形ABC 中，====AD BC D BC AC AB 的中点，则为，，，864().A.11B.10C.3D.22 E.711.某单位要铺设草坪，若甲、乙两公司合作需6天完成，工时费共计2.4万元；若甲公司单独做4天后由乙公司接着做9天完成，工时费共计2.35万元，若由甲公司单独完成该项目，则工时费共计().A.2.25万元 B.2.35万元 C.2.4万元 D.2.45万元 E.2.5万元12.如图，六边形ABCDEF 是平面与棱长为2的正方体所截得到的，若E D B A ,,,分别是相应棱的中点，则六边形ABCDEF 的面积为().A.23B.3 C.32 D.33 E.3413.货车行驶72千米用时1小时，其速度v 与行驶时间t 的关系如图所示，则=0v ().A.72B.80C.90D.95E.10014.某中学的五个学科各推荐了2名教师作为支教候选人，若从中选派来自不同学科的2人参加支教工作，则不同的选派方式有()种.A.20 B.24 C.30 D.40 E.4515.设数列{}==-=+10011,12,0a a a a a n n n 则满足().A.1299- B.992C.1299+ D.12100- E.12100+二．条件充分性判断：第16-25小题，每小题3分，共30分。

2222019 年全国硕士研究生入学统一考试真题管理类综合能力一、问题求解： 第 1— 15 小题，每小题 3 分，共 45 分。

下列每题给出的 A 、B 、C 、D 、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项的字母涂黑。

1、某车间计划 10 天完成一项任务，工作了 3 天后因故停工 2 天，若要按原计划完成任务， 则工作效率需要提高（） A.20%B.30%C.40%D.50%E.60%【解析】 7 天工作量由 5 天完成，工作效率由17提高到 1，提高的百分比为 51 15 7 1 7 =40%2、设函数 f (x) 2xa 2 （a ＞0）在（ 0， +∞）内的最小值为f (x 0) 12 ， 则 x0=（）。

xA.5B.4C.3D.2E.13、某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数之比为（） 。

A.3:4B.5:6C.12:13D.13:12E.4:3女性观 众 3月份人 1月份数2月份 单位：万人4、设实数 a ， b 满 足 ab=6， a b a b 6 ，则 ab1 01男性观众人数A.10B.11C.12D.13E.14( x 5、设圆 C 与圆5) 2 y 22 关于直线 y=2x 对称，则圆 C 的方程为（） 。

A. ( x 3)2( y 4)22 B. ( x 4)2( y 3)22 C. ( x3)2( y 4)22 D. ( x3)2( y 4)22E. ( x 3)( y 4)226、在分别记了数字1、2、3、4、5、6 的6 张卡片中，甲随机抽取 1 张后，乙从余下的卡片中再随机抽取 2 张，乙的卡片数字之和大于甲的卡片数字的概率为（）。

11 13A. B. C.60 60 43 47 49D. E.60 60 607、将一批树苗种在一个正方形花园的边上，四角都种，如果每隔 3 米种一颗，那么剩余10 颗树苗，如果每隔 2 米种一颗那么恰好种满正方形的 3 边，则这批树苗有（）。

2019年MBA英语试题及答案一、阅读理解（共20分，每题2分）1. What is the main idea of the passage?A. The importance of teamwork in businessB. The role of technology in businessC. The impact of globalization on businessD. The challenges of managing a business答案：A2. According to the passage, which of the following is NOT a benefit of teamwork?A. Improved communicationB. Increased creativityC. Reduced workloadD. Enhanced problem-solving答案：C3. The author suggests that technology can help businesses by:A. Reducing costsB. Expanding marketsC. Improving customer serviceD. All of the above答案：D4. What is the impact of globalization on businesses?A. Increased competitionB. Access to new marketsC. Both A and BD. Neither A nor B答案：C5. What does the author recommend for effective business management?A. Focusing on short-term profitsB. Prioritizing customer satisfactionC. Ignoring external factorsD. Relying solely on intuition答案：B二、完形填空（共20分，每题2分）6. The company has been _______ the market for years, but now it's time to expand.A. dominatingB. exploringC. controllingD. targeting答案：A7. Despite the initial success, the team faced _______ challenges as they moved forward.A. numerousB. minorC. occasionalD. trivial答案：A8. The manager emphasized the need for _______ when dealing with clients.A. transparencyB. flexibilityC. assertivenessD. patience答案：A9. The new strategy was _______ by the board, but it still required careful planning.A. approvedB. rejectedC. postponedD. ignored答案：A10. The company's reputation was _______ by its commitment to quality and service.A. enhancedB. damagedC. maintainedD. diminished答案：A三、翻译（共20分，每题4分）11. 随着互联网的普及，电子商务已经成为许多企业增长的关键驱动力。

2019全国MBA联考综合能力真题及答案-解析一、单选题（共55题，共110分）1.某车间计划10 天完成一项任务，工作3 天后事故停工2 天，若仍要按原计划完成任务，则工作效率要提高( ).• A.20%• B.30%• C.40%• D.50%• E.60%ABCDE正确答案：C本题解析：整个工程看做单位"1" ，原计划的工作效率为1/10 ，实际的工作效率为(1-1/10x3)/( 10-3-2) =7/50 ，因此工作效率提高了(7/50-1/10)/(1/10)=40% ，选C。

2.函数f(x)=2x+a/ π2(a ﹥0) ，在(0 ，+ ∞)内最小值为f(x 0)=12 ，则x0=• A.5• B.4• C.3• D.2• E.1ABCDE正确答案：B本题解析：利用三个数的均值定理求最值：a+b+c ≥3 3 √abc 。

f(x)=2x+a/x 2 =x+x+a/x 2≥3 3√x*x*a/x 2，因此最小值为3 3√a=12 →a=64 ，因此x=x=64/x 2→x=4 ，选B。

3.某影城统计了一季度的观众人数，如图，则一季度的男、女观众人数为（）。

• A.3:4• B.5:6• C.12:13• D.13:12• E.4:3ABCDE正确答案：C本题解析：如图可得：一季度男女观众人数分別为:男: 5w+ 4w+ 3w= 12w女: 6w+ 3w+ 4w= 13w故一季度男女人数比的: 12:13 ，选C。

4.没实数a,b 満足ab=6 ，|a+b| +|a-b|=6 ，则a2+b2=( )• A.10• B.11• C.12• D.13• E.14ABCDE正确答案：D本题解析：ab=6, 特值法a=2 ，b=3 満足条件，a2+b2=4+9=13 ，选D。

5.设圆C 与圆(x-5) 2+y2=2 ，关于y=2x 时称，则圆C 方程为( )• A.(x-3) 2 +(y-4) 2=2• B.(x+4) 2 +(y-3) 2=2• C.(x-3) 2 +(y+4) 2=2• D.(x+3) 2 +(y+4) 2=2• E.(x+3) 2 +(y-4) 2=2ABCDE正确答案：E本题解析：暂无解析6.将一批树苗种在应该正方形花园边上，四角都种，如果每隔3 米种一棵，那么剩下10课树苗,如果每隔2 米种一棵那么种满正方形的3 条边,则这批树苗有( ) 棵• A.54• B.60• C.70• D.82• E.94ABCDE正确答案：D本题解析：设正方形的边长为x，由已知可得方程4x/3+10=3x/2+1 ，求解得x=54故树苗有(54x4)/3+10=82 ，选D。

2017年管理类专业联考综合能力数学试题及解析一、问题求解：第1~15小题，每小题3分，共45分。

下列每题给出的A ．B ．C ．D ．E 五个选项中，只有一项是符合试题要求的，请在答题卡上将所选项的字母涂黑。

1、某品牌的电冰箱连续两次降价10%后的售价是降价前的（） %%%%%2、甲、乙、丙三种货车的载重量成等差数列，2辆甲种车和1辆乙种车满载量为95吨，1辆甲种车和3辆丙种车满载量为150吨。

则用甲、乙、丙各1辆车一次最多运送货物（）吨3、张老师到一所中学进行招生咨询，上午接受了45名同学的咨询，其中的9名同学下午又咨询了张老师，占张老师下午咨询学生的10%。

一天中向张老师咨询的学生人数为（）4、某种机器人可搜索到的区域是半径为1米的圆，若该机器人沿直线行走10米。

其搜索过的区域的面积（单位：平方米）为（） A.102π+B.10π+C.202π+D.20π+E.10π5、不等式12x x -+≤的解集为（） A.(],1-∞B.3,2⎛⎤-∞ ⎥⎝⎦C.31,2⎡⎤⎢⎥⎣⎦D.[)1,+∞E.3,2⎡⎫+∞⎪⎢⎣⎭6、在1与100之间，能被9整除的整数的平均值为（）7、某试卷由15道选择题组成，每道题有4个选项，只有一项是符合试题要求的，甲有6道题能确定正确选项，有5道题能排除2个错误选项，有4道题能排除1个错误选项。

若从每题排除后剩余的选项中选1个作为答案，则甲能得满分的概率为（）A.451123⋅B.541123⋅C.541123+D.541324⎛⎫⋅ ⎪⎝⎭E.541324⎛⎫+ ⎪⎝⎭8、某公司用1万元购买了价格分别是1750元和950元的甲、乙两种办公设备，则购买的甲、乙办公设备的件数分别为（） ,5,3,4,6,29、如图1，在扇形AOB 中，,1,4AOB OA AC OB π∠==⊥，则阴影部分的面积为（）A.184π- B.188π- C.142π-图1D.144π- E.148π- 10、老师问班上50名同学周末复习的情况，结果有20人复习过数学，30人复习过语文，6人复习过英语，且同时复习了数学和语文的有10人，语文和英语的有2人，英语和数学的有3人。

2019年管理类MBA综合考试数学真题及详细答案解析一、问题求解：第1～15小题，每小题3分，共45分。

下列每题给出A、B、C、D、E五个选项中，只有一项是符合试题要求的。

请在答题卡上将所选项字母涂黑。

1. 学科竞赛设一等奖、二等奖和三等奖，比例为1：3：8，获奖率为30%，已知10人获得一等奖，则参加竞赛的人数为（）A．300 B. 400 C. 500 D. 550 E. 600解析：（B）解法1：由一等奖：二等奖：三等奖=1：3：8，且一等奖10人，可推出二等奖、三等奖分别为30人和80人，所以获奖人数为10+30+80=120人，所以参加竞赛人数为12030%=400÷人。

解法2：设参加竞赛的人数为x，根据题意有130%10400138x x=⇒=++。

2. 为了解某公司员工的年龄结构，按男、女人数的比例进行了随机抽样，结果如下：A. 32, 30B. 32, 29.5C. 32, 27D. 30, 27E. 29.5, 27解析：（A）23+26+28+30+32+34+36+38+41==329x男23+25+27+27+29+31==276x 女329+276==3015x⨯⨯总3. 某单位采取分段收费的方式收取网络流量(单位: GB)费用，每月流量20(含)以内免费，流量20到30(含)的每GB收费1元，流量30到40(含)的每GB收费3元，流量40以上的每GB收费5元，小王这个月用了45GB的流量，则他应该交费（）A. 45元B. 65元C. 75元D. 85元E. 135元解析：（B）各个流量段所需缴费数额见下表：所以小王应该缴费0+10+30+25=65元。

4. 如图，圆O 是三角形ABC 的内切圆，若三角形ABC 的面积与周长的大小之比为1:2，则圆O 的面积为( ) A. π B.2π C. 3π D. 4π E. 5π解析：（A ）解法1：设三角形边长分别为,,a b c ，内切圆O 的半径为r ，则三角形周长L a b c =++，三角形面积12S Lr =(最好记住该结论)。

考研管理类联考综合能力真题答案及解析（完整版）来源：文都教育一、问题求解：第1~15小题，每小题3分，共45分，下列每题给出的A 、C 、C 、D 、E 五个选项中，只有一项是符合试题要求的。

1.学科竞赛设一、二、三等奖，比例1：3：8获奖率30%，已知10人已获一等奖，则参赛人数（B ）A.300B.400C.500D.550E.600男员工年龄（岁）23 26 28 30 32 34 36 38 41 女员工年龄（岁）23 25 27 27 29 31据表中数据统计，该公司男员工的平均年龄与全体员工平均年龄分别是（ A ）A.32，30B.32，29.5C.32，27D.30，27E.29.5，273.某单位分段收费收网站流量（单位：GB ）费：每日20（含）GB 以内免，20到30（含）每GB 收1元，30到40（含）每GB 3元，40以上每GB 5元，小王本月用45GB 该交费（B ）A.45B.65C.75D.85E.1354.圆O 是△ABC 内切圆△ABC 面积与周长比1:2，则图O 面积（A ）A.πB.2πC.3πD.4πE.5π 5.实数满足， 则（E ）A.30B.22C.15D.13E.106.6张不同卡片两张一组分别装入甲乙丙3个袋中，指定两张要在同一组，不同装法有（ B ）种，A.12B.18C.24D.30E.36 7.四边形A 、B 、C 、D 是平行四边形，是四边的中点是四边中点依次下去，得到四边形序列设面积为且则（C ）A.16B.20C.24D.28E.30 8.甲乙比赛围棋，约定先胜2局者胜，已知每局甲胜概率0.6，乙为0.4，若第一局乙胜，则甲赢得比赛概率为（C ）A.0.144B.0.288C.0.36D.0.4E.0.6 9.圆，若圆在点（1，2）处的切线与轴及点为（0.3）则=（E ）A.-2B.-1C.0D.1E.210.96顾客至少购甲、乙、丙3种商品中一种，经调查同时购甲、乙两种的有8位，同时购甲丙的有12位，同购乙、丙的有6位，同购3种的有2位，则仅购一种的有（C ）A.70位B.72C.74D.76E.82,a b ||2a b -=22a b +=2222A B C D 1111A B C D 3333A B C D 2222A B C D (123)n n n n A B C D n =、、…n n n n A B C D n S 112S =123S S S +++…=22:()C x y a b +-=C y ab11.函数22()max{,8}f x x x =-+的最小值为（B ） A.8 B.7 C.6 D.5 E.412.某单位为检查3个印前工作，由这3个部门主任和外聘3名人员组成检查组，每组1名外聘，规定本部门主任不能检查本部门，则不同的安排方式有（C ）A.6种B.8种C.12种D.18种E.36种13.从标号1到10中的10张卡片中随抽2张，而它们的标号2种能被5整除的概率（A ）A. B. C. D. E. 14.圆柱体底面半径2，高3，垂直于底面的平面截圆柱体所得截面为矩形，若弦所对圆心角是，则截去部分（较小那部分）体积（D ）A. B.C.33π-D.233π-E.15.羽毛球队4名男运动员3女足动员，从中选出2对参加混双比赛，不同选派方式（D ）A.19B.18C.24D.36E.72二、条件充分性判断：第16~25小题，每小题3分，共30分。

2019mba管综试题及答案2019MBA管理类联考综合能力测试试题及答案【试题一】题目：请分析企业文化对员工行为的影响，并结合实际案例进行说明。

答案：企业文化是企业在长期发展过程中形成的共同价值观、行为准则和精神面貌的总和。

它对员工的行为有着深远的影响。

首先，企业文化能够塑造员工的价值观，引导员工形成与企业目标一致的行为模式。

例如，谷歌公司的“不作恶”原则，就鼓励员工在创新和工作中追求正直和道德。

其次，企业文化通过行为准则来规范员工的日常行为，如华为公司的“狼性文化”，强调团队协作和对目标的执着追求，这使得员工在工作中展现出极高的执行力和团队精神。

最后，企业文化还能够激发员工的内在动力，提高工作满意度和忠诚度。

比如，星巴克的“第三空间”理念，不仅为顾客提供了一个舒适的社交场所，也让员工感受到工作的价值和意义。

【试题二】题目：简述SWOT分析法，并给出一个实际应用案例。

答案：SWOT分析法是一种战略规划工具，用于评估组织的优势（Strengths）、劣势（Weaknesses）、机会（Opportunities）和威胁（Threats）。

通过这种分析，组织可以更好地理解自身的竞争地位，制定相应的战略。

优势是指组织内部的资源和能力，这些可以为组织带来竞争优势。

劣势是指可能影响组织绩效的内部限制因素。

机会是外部环境中可能带来增长和成功的条件。

威胁是外部环境中可能对组织造成损害的条件。

以苹果公司为例，其优势包括强大的品牌影响力和创新能力；劣势可能是对单一产品的依赖度过高。

机会可能来自于新技术的发展和新兴市场的扩张；威胁可能来自于竞争对手的激烈竞争和市场饱和度的增加。

【试题三】题目：论述平衡计分卡在企业管理中的应用及其重要性。

答案：平衡计分卡是一种绩效管理工具，它通过将组织的愿景和战略转化为一组绩效指标来监控企业的绩效。

这些指标通常分布在四个维度：财务、客户、内部流程和学习与成长。

平衡计分卡的重要性在于它帮助企业实现多维度的管理，不仅仅关注短期的财务指标，也重视长期的客户满意度、内部流程效率和员工能力的提升。

2019年mba真题科创板成了资本大佬们的必争之地。

这其中，雷军和他的小米是最闪亮的那颗星。

据不完全统计，雷军本人或者小米持股的科创板IPO申报企业已经达到了9家。

这些公司，有的从出生便有小米一路扶持，到现在“独立”行走寻求上市，它们是小米生态链上的企业，小米将他们称为兄弟；也有的是突击入股，为的可能是蹭一波科创板的红利，实现投资收益。

近几年，小米对外投资超过210起，涉及的行业20余个，这些投资也为小米带来了高额的收益。

2019年1季度，小米投资带来的公允价值变动收益就高达26.3亿元，占其当期净利润的82%。

但与其大手笔投资和丰厚的投资利润相比，小米对于自身的科技建设显得十分吝啬。

其研发开支占营收的比例一直在3%徘徊，别说和华为比了，即使是和在科创板申报上市的公司来说也逊色不少，雷军在公开信中曾言：“创新科技和顶尖设计是小米基因中的追求！”而当投资的企业一个个实现证券化，投资收益一点点变成小米的支柱，其创新和钻研的动力可还存在？风口永远是资本追逐的方向。

小米手机就是风口论的成功印证，当然，风口论也并非鼓吹投机，而是要摸准时代的脉搏，顺势而为。

小米手机正是站到了移动互联网的风口，赶上了换机潮，才在手机领域杀出了一片天地。

沿着互联网到移动互联网再到物联网（IoT）的发展路径，物联网成为下一个时代的趋势。

2013年，小米意识到IoT的风口不远，于是为抢跑IoT而生的小米生态链启航了。

以生态链企业石头科技为例，这家公司成立于2014年7月，9月便成为了生态链的一员。

有了小米的助攻，石头科技实现了迅猛增长。

短短4年的时间，石头科技的收入达到了30亿元，年复合增长率高达308%，净利润也超过3亿元，这离不开小米的口碑和渠道支持。

初期，石头科技为小米提供订制产品“米家扫地机器人”和相关备件。

石头科技根据小米的产品规划进行产品设计和开发，然后将设计委托给第三方进行加工，生产完成后交给小米，米家扫地机器人会在小米商城等平台售卖。