人教版六年级数学上册百分数的应用题1优秀课件
- 格式:pptx
- 大小:299.31 KB
- 文档页数:16


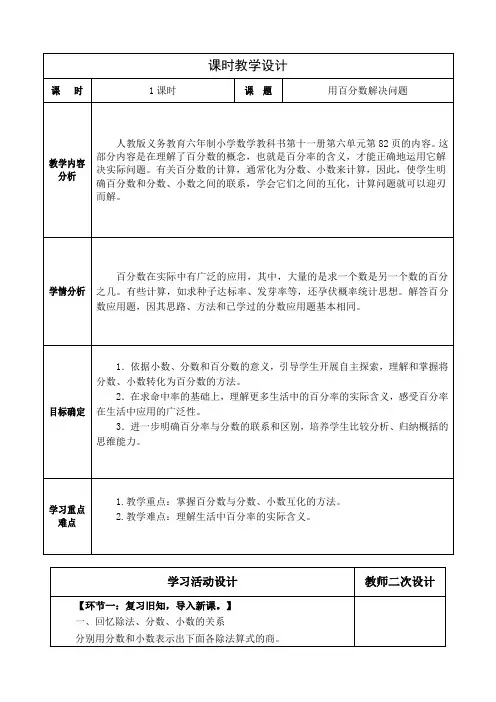
1÷2= 3÷20=4÷5= 8÷25=3÷8= 7÷50=9÷10= 43÷100=小结:我们学过了整数、小数、分数之间的相互转化,那分数、小数又怎么转化成百分数呢,今天我们来一起探究。
[设计意图:通过回顾旧知识,让学生容易找到新旧知识之间的联系,进而用转化的思想来解决新问题。
]【环节二:自主活动,探究新知。
】师:王涛和李强是各自篮球队的主要得分手。
在一场比赛后,他们之间有这样一段对话(课件出示)。
从图中你能获得哪些信息?预设:王涛是5投3中,李强是6投4中。
师:根据这两条信息,你想知道什么?(谁的投篮更准)该怎么比较呢?学生计算,指名回答。
预设1:,,因为,所以李强的投篮更准。
预设2:,,因为,所以李强的投篮更准。
师:这两种算法有什么相同的地方?(算式相同)都是求什么?(命中率,即投中的次数占投篮总次数的几分之几)有什么不同呢?(一个是用小数表示结果,一个是用分数表示结果)1.揭示命中率。
师:这种计算的方法,与篮球比赛技术统计中的投篮命中率类似。
从百分数的意义出发进行思考,什么叫“投篮命中率”?根据学生回答逐步概括为:投篮命中率表示投中次数占投篮总次数的百分之几。
追问:该如何计算呢?。
师:这个题目的问题是“他们两人的命中率分别是多少?谁的命中率高?”。
2.分数、小数与百分数的互化。
师:投篮命中率是一个什么数?(百分数)你能把刚才的两种运算结果转化成百分数吗?学生练习,指名回答。
预设1:。
你是怎么做的?(把小数化成分母是100的分数,再化成百分数。
)预设2:。
师:除不尽,怎么办?看书本上是怎么解决的?(除不尽时,通常保留三位小数。
)预设:或。
师:你能解释这里的“≈”和“=”符号的用法吗?(除不尽,保留三位小数约等于0.667。
然后把0.667这个小数转化为分母是1000的分数,是相等关系。
)师:这样我们已经分别计算出了两个人的命中率,谁更高些?(李强)3.引导归纳,得出方法。

期末备考—人教版六年级上册数学优选题单元复习讲义第六单元《百分数(一)》一、百分数1、表示一个数是另一个数的百分之几的数叫做百分数。
百分数又叫百分比或百分率,百分数不能带单位。
注意:百分数是专门用来表示一种特殊的倍比关系的,表示两个数的比。
2、百分数和分数的区别和联系(1)联系:都可以用来表示两个量的倍比关系。
(2)区别:意义不同:百分数只表示倍比关系,不表示具体数量,所以不能带单位。
分数不仅表示倍比关系,还能带单位表示具体数量。
百分数的分子可以是小数,分数的分子只可以是整数。
3、小数、分数、百分数之间的互化(1)百分数化小数:小数点向左移动两位,去掉“%”。
(2)小数化百分数:小数点向右移动两位,添上“%”。
(3)百分数化分数:先把百分数写成分母是100的分数,然后再化简成最简分数。
(4)分数化百分数:分子除以分母得到小数,(除不尽的保留三位小数)然后化成百分数。
(5)小数化分数:把小数成分母是10、100、1000等的分数再化简。
(6)分数化小数:分子除以分母。
二、百分数应用题1、求常见的百分率如:达标率、及格率、成活率、发芽率、出勤率等求百分率就是求一个数是另一个数的百分之几。
2、求一个数比另一个数多(或少)百分之几实际生活中,人们常用增加了百分之几、减少了百分之几、节约了百分之几等来表示增加、或减少的幅度。
求甲比乙多百分之几:(甲-乙)÷乙求乙比甲少百分之几:(甲-乙)÷甲3、求一个数的百分之几是多少一个数(单位“1”)×百分率4、已知一个数的百分之几是多少,求这个数部分量÷百分率=一个数(单位“1”)5、折扣、打折的意义几折就是十分之几也就是百分之几十折扣、成数=几分之几、百分之几、小数八折=八成=十分之八=百分之八十=0.8八五折=八成五=十分之八点五=百分之八十五=0.85五折=五成=十分之五=百分之五十=0.5=半价6、利率(1)存入银行的钱叫做本金。


人教版六年级上册数学百分数(一)应用题同步练习1.在家电下乡活动期间,一台电视机按定价的90%销售,店老板还承诺,除此以外每台电视机还享受财政补贴200元,且返路费50元。
照这样,王师傅买了一台电视机,花了2270元。
这台电视机的定价是多少元?2.宁宁读一本书,第一天读了全书的30%,第二天比第一天少读了15页,这时还有一半没有读。
这本书一共有多少页?3.光明小学进行校园改造,对学校的围墙进行重修,第一天修了20米,正好是围墙总长度的25%,学校要重修的围墙一共长多少米?4.饲养小组养了36只白兔,12只灰兔,白兔和灰兔分别占总只数的百分之几?5.李师傅对一批机器零件做抽样检查,从抽查的80个零件看,有78个合格,2个不合格。
(1)这批零件的合格率是多少?(2)不合格率是多少?5.李大伯家的一块菜地,种西红柿的面积占菜地面积的38%,种黄瓜的面积占菜地面积的38。
哪种菜占地面积大?7.修一条路,第一个月修了全部的14%,第二个月修了全部的15%。
已知这两个月一8.工地有一堆沙子,第一次运走全部的23%,第二次运走全部的18%,还剩下472吨,那么这堆沙子原来有多少吨?9.甲与乙的比是5∶6,乙与丙的比是4∶5,乙比丙少百分之几?丙比甲多百分之几?10.晓东一家寒假出去旅游,他们一家支出费用如图:(1)门票费用支出400元,请你算一算他们一家旅游总支出是多少?(2)费用支出最多的是(),是()元。
11.图书馆有甲、乙两个书架,从甲书架取出图书总数的20%,剩下的图书数量刚好与乙书架上的图书相等。
乙书架共有40本图书,甲书架原来一共有多少本图书?12.一块锡和铅的合金重27千克,含铅率是60%,这块合金含铅多少千克?13.六(2)班今天有48人来上课,有2人请假,求这一天六(2)班的出勤率。
14.修一条公路,第一天修了全长的20%,第二天修了全长的35%,两天一共修了5500米,这条公路一共有多长?15.水果市场有橘子450千克,苹果比橘子少20%,比梨多12.5%,水果批发市场有梨多少千克?16.运输公司前年耗油100吨,去年耗油80吨。





第六单元百分数(一)(讲义)学校数学六班级上册专项训练(学问梳理+典例精讲+专项训练)1.百分数的意义。
百分数的意义:表示一个数是另一个数的百分之几,百分数也叫作百分率或百分比。
2.百分数的读、写法。
百分数的读法:先读百分号,再读百分号前面的数。
留意:“%”读作“百分之”而不是“一百分之”。
百分数的写法:把分母写成百分号“% ”,分子写在百分号前面。
3.百分数与小数的互化。
百分数化成小数:先把百分号去掉,然后把小数点向左移动两位,位数不够时用“0”补足。
小数化成百分数:把小数点向右移动两位,并在后面添上百分号。
4.百分数与分数的互化。
百分数化成分数:先把百分数写成分母是100的分数,然后能约分的要约成最简分数。
分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),然后把小数化成百分数。
5.常见的百分率的计算方法。
6.求一个数是另一个数的百分之几的问题的解法。
与求一个数是另一个数的几分之几的解题方法基本相同,即用“比较量÷标准量”来计算,其最终结果要化成百分数。
7.求一个数的百分之几是多少的问题的解法。
一个数(单位“1”)×百分率=所求的数8.求一个数比另一个数多(或少)百分之几的实际问题的解法。
实质上是求两个数的差量占另一个数的百分之几。
假设其中一个量是甲,另一个量是乙:(1)求甲比乙多百分之几,列式为(甲-乙)÷乙或甲÷乙-100%。
(2)求乙比甲少百分之几,列式为(甲-乙)÷甲或100%-乙÷甲。
9.求比一个数多(或少)百分之几的数是多少的问题的解法。
方法一:单位“1”的量±单位“1”的量×另一个量比单位“1”的量多(或少)百分之几=另一个量。
方法二:单位“1”的量×[1±另一个量比单位“1”的量多(或少)百分之几]=另一个量。
【典例一】据调查,英才学校同学的近视率是6%,光明学校同学的近视率也是6%。
六年级数学上册典型例题系列之第六单元百分数的应用题其一:百分数与分数乘除法应用题的结合(解析版)编者的话:《六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结和编辑而成的,其优点在于选题典型,考点丰富,变式多样。
本专题是第六单元百分数的应用题其一:百分数与分数乘除法应用题的结合,后续内容为《第六单元百分数的应用题其二:百分数与比应用题的结合》、《第六单元百分数的应用题其三:百分率问题》和《第六单元百分数的应用题其四:浓度问题》。
本部分内容是百分数与分数乘除法应用题的结合问题,由于分数乘除法应用题主要体现在第一、三单元的内容中,所以,本部分内容考点划分较为笼统,分数乘除法应用题详细内容请参考第一、三单元的典型例题系列。
该部分内容多考察填空、选择、应用等题型,综合性较强,题目难度稍大,建议结合分数乘除法应用题作为重点部分和复习内容进行讲解,共划分为六个考点,欢迎使用。
【考点一】百分数与分数乘法应用题的结合其一:基本类型题。
【方法点拨】1.百分数应用题多是在分数乘除法应用题的基础上进行变式,因此,掌握了分数乘除法应用题也就掌握了百分数应用题。
(注意:分数乘除法应用题的详细考点请参考编者的第一、三单元典型例题系列)2.百分数应用题与分数乘法应用题的结合:(1)求一个数的百分之几是多少?(单位“1”已知)单位“1”×百分率=分率所对应的量(2)求一个数比另一个数多(少)百分之几的数是多少?单位“1”×(1+百分率)=分率所对应的数量【典型例题1】东风化肥厂九月份计算生产化肥2800万袋,实际上半月完成计划的59%,下半月完成计划的65%。
全月超额生产化肥多少袋?解析: 2800×(59%+65%)-2800=672(袋)答:略。
【典型例题2】从1997年至今,我国铁路进行多次提速。
有一列火车,原来每小时行驶80千米,提速后,这列火车的速度比原来增加了40%。
现在这列火车每小时行驶多少千米?解析:80×(1+40%)=112(千米)答:略。