复合材料力学讲义(试题学习)
- 格式:doc
- 大小:340.50 KB
- 文档页数:26

复合材料试题参考答案及评分标准请将所有答案写在答题纸上。
一、判断题(2分×10=20分)1.复合材料的自振频率比单一材料要低, 因此可以避免工作状态下的共振。
2.玻璃陶瓷又称微晶玻璃。
3.纤维与金属类似, 也有时效硬化现象。
4.立方型的BN, 因在结构上类似石墨而具有良好的润滑性。
5.在溶解与润湿结合方式中, 溶解作用是主要的, 润湿作用是次要的。
6.石墨纤维的制造与Al2O3纤维类似, 都是采用直接法。
7.纯金属的表面张力较低, 因此很容易润湿纤维。
8.E-玻璃纤维具有良好的导电性能。
9.良好的化学相容性是指高温时复合材料的组分之间处于热力学平衡, 且相与相之间的反应动力学十分缓慢。
10.(TiB+TiC)/Al是一种混杂复合材料。
二、填空题(1分×18=18分)1.Bf/Al 复合材料的界面结合以()为主。
2.纤维增强CMCs的断裂模式有()、()、和()。
3.非线性复合效应有()、()、()和()。
4.复合材料的设计类型有()、()、()、()和()。
5.CVD法制造B f的芯材通常有()、()、()和()。
原位复合材料中, “原位”是指()。
三、简答题(4分×5=20分)1.池窑拉丝法在那些方面比坩埚法生产玻璃纤维更为先进?2.温度因素是如何影响复合材料中基体对增强体的润湿性?3.Bf表面为什么通常要进行涂层?4.简述现代界面模型的主要观点。
纤维增强ZrO2复合材料的主要增韧机制有哪些, 并简述其增韧原理。
四、问答题1.说明连续纤维增强复合材料的横向弹性模量遵循混合效应(12分)。
2.写出2种液态法制造MMCs的方法, 并简述其工艺过程和优缺点(12分)。
画出CMCs的应力-应变曲线, 将其与低碳钢作比较;简述CMCs在拉伸载荷作用下的断裂过程, 画出示意图。
(20分)一、判断题1×2√3×4×5×6×7×8×9√10√(每小题2分)1.二填空题(每空1分, 共18分)2.机械结合3.脆性断裂韧性断裂混合断裂4.相乘效应诱导效应系统效应共振效应5.安全设计单项性能设计等强度设计等刚度设计优化设计6.钨丝碳丝涂钨的石英纤维涂碳的石英纤维增强体不是采用外加方法进入基体的, 而是通过化学反应的方法在基体内部生成的三简答题1.(1)池窑拉丝法采用的漏板上小孔数目大幅度增加, 提高了拉丝效率;(2)池窑拉丝采用玻璃料直接熔化而不是采用玻璃小球, 提高了原料利用率(3)池窑拉丝的废料可以直接再熔化, 减少了浪费满分4分, (2), (3)共2分。

习 题一、 单向纤维板受力后发生面内变形,%4.0=x ε,%2.0=y ε, %1.0=xy γ,纤维与x 轴夹角为︒=30θ ,求该材料主轴坐标系下的应变分量。
二、已知碳/环氧单向板的工程弹性常数为:GPa E L 140=,GPa E T 10=,GPa G LT 5=, 3.0=TL ν,求柔量分量ij S 和模量分量ij Q 。
若材料主轴方向的应力状态为:MPa 501=σ,MPa 302=σ,MPa 2512=τ,计算单向板的应变。
三、复合材料单向板承受偏轴向压缩(︒=60θ),MPa y 160-=σ。
[1] 求在材料主轴向下的应力分量和应变分量。
[2] 分别用最大应力准则、蔡-希尔和Hoffman 准则判断该板是否安全。
已知单向板的主轴向柔量和强度参数分别为:111)(20-=TPa S , 122)(200-=TPa S112)(12--=TPa S , 166)(250-=TPa SMPa X t 1200=, MPa X c 900= MPa Y t 48=, MPa Y c 180=, MPa S 70=-----------------------------------------------------------------------------------------------四、 正交铺设对称层合板[]0/90s 受到拉伸,mm N N x /400=,单层厚度为 mm t k 2.0=,求各铺层应力。
已知:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=80012303150Q GPa 五、 由碳/环氧复合材料制成的对称层合板[0/45/90]S ,受正则化面内力MPa N xy 50*= 的作用,求各铺层应变和应力。
已知:[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=6.5004.108.308.3160Q GPa 六、 正交铺设对称层合板[]0/90s ,单层厚度为 mm t k 2.0=,单层模量为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=5.10004.256.806.8120Q GPa [1] 计算层合板的刚度; [2] 确定合力-变形关系式;[3] 层合板沿x 方向受到拉伸,)/(200mm N N x =, 求各铺层应力。

《复合材料结构设计》习题§1 绪论1.1 什么是复合材料?1.2 复合材料如何分类?1.3 复合材料中主要的增强材料有哪些?1.4 复合材料中主要的基体材料有哪些?1.5 纤维复合材料力学性能的特点哪些?1.6 复合材料结构设计有何特点?1.7 根据复合材料力学性能的特点在复合材料结构设计时应特别注意到哪些问题?§2 纤维、树脂的基本力学性能2.1 玻璃纤维的主要种类及其它们的主要成分的特点是什么?2.2 玻璃纤维的主要制品有哪些?玻璃纤维纱和织物规格的表示单位是什么?2.3 有一玻璃纤维纱的规格为2400tex,求该纱的横截面积(取玻璃纤维的密度为2.54g/cm3)?2.4 有一玻璃纤维短切毡其规格为450 g/m2,求该毡的厚度(取玻璃纤维的密度为2.54g/cm3)?2.5 无碱玻璃纤维(E-glass)的拉伸弹性模量、拉伸强度及断裂伸长率的大致值是多少?2.6 碳纤维T-300的拉伸弹性模量、拉伸强度及断裂伸长率的大致值是多少?密度为多少?2.7 芳纶纤维(kevlar纤维)的拉伸弹性模量、拉伸强度及断裂伸长率的大致值是多少?密度为多少?2.8 常用热固性树脂有哪几种?它们的拉伸弹性模量、拉伸强度的大致值是多少?密度为多少?热变形温度值大致值多少?2.9 简述单向纤维复合材料抗拉弹性模量、抗拉强度的估算方法。
2.10 试比较玻璃纤维、碳纤维单向复合材料顺纤维方向拉压弹性模量和强度值,指出其特点。
2.11 简述温度、湿度、大气、腐蚀质对复合材料性能的影响。
2.12 如何确定复合材料的线膨胀系数?2.13已知玻璃纤维密度为ρf=2.54g/cm3,树脂密度为ρR=1.20g/cm3,采用规格为450 g/m2的玻璃纤维短切毡制作内衬时,其树脂含量为70%,这样制作一层其GFRP的厚度为多少?2.14 采用2400Tex的玻璃纤维(ρf=2.54g/cm3)制造管道,其树脂含量为35%(ρR=1.20g/cm3),缠绕密度为3股/10 mm,试求缠绕层单层厚度?2.15 试估算上题中单层板顺纤维方向和垂直纤维方向的抗拉弹性模量和抗拉强度。

复合材料力学试题答案判断题(正确的在括弧内划√,错误的在括弧内划×)。
1.“宏观力学”是在研究复合材料力学性能时,假定材料是均质的。
(√)2.单层是层合板的基本单元,在复合材料结构设计中又叫做三次结构。
(×)3.层合板由若干具体不同纤维方向的单层叠合而成,在复合材料机构设计中又叫二次结构。
(√)4.复合材料力学中,1为纵向,2为横向,应力规定拉为负,压为正。
(×)5.在单层板(正交各向异性)材料中,τ12不仅形成剪切变形,还存在剪拉耦合效应。
(×)6.在单层正交各向异性板中,11)1(11σεE =。
(√) 7.在单层正交各向异性板中,11122)1(2)2(221συσεεεE E -=+=。
(√) 8.单层板的工程弹性常数有5个,且相互独立。
(×)9.柔量矩阵{S}是对称矩阵,而模量举证{Q}不是对称矩阵。
(×)10.在正交单层板中,Q16=Q26=0,Q61=Q62,但其值不为零。
(×)11.在复合材料力学中,对于工程弹性常数存在如下关系:2121υυ=E E 。
(√) 12.在单层板偏轴刚度中,应力转换和应变转换关系式中,m=sin θ,n=cos θ。
(×)13. 在单层板偏轴刚度中,应力转换和应变转换关系式中存在如下关系:[][][]T T T 1-=σε。
(√)14.在ij Q 中,11Q 、22Q 是θ的偶函数,16Q 、26Q 也是θ的偶函数。
(×) 15.玻璃钢复合材料在拉伸时发生变形,所以是一种塑性材料。
(×)16.利用复合材料的强度准则,可以判断复合材料设计过程的安全性,同时可以计算极限载荷。
(×)17.利用最大应力准则判断材料安全性时,如果判断式大于1,说明材料的机构是安全的。
(×)18.在复合材料中,利用强度比可以计算复合材料的极限载荷。
(√)20.在对称层合板中,)()(z z --=θθ。


《复合材料力学》考试题1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.5×104MPa,环氧E m =3.5×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =60GPa,E2 =20GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.0×104MPa,环氧E m =3.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =55GPa,E2 =17.5GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =8.0×104MPa,环氧E m =4.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =65GPa,E2 =22GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。

复合材料力学讲义第一部分简单层板宏观力学性能1.1各向异性材料的应力—应变关系应力—应变的广义虎克定律可以用简写符号写成为:(1—1)其中σi 为应力分量,Cij为刚度矩阵εj为应变分量.对于应力和应变张量对称的情形(即不存在体积力的情况),上述简写符号和常用的三维应力—应变张量符号的对照列于表1—1。
按表1—l,用简写符号表示的应变定义为:表1—1 应力——应变的张量符号与简写符号的对照注:γij (i≠j)代表工程剪应变,而εij(i≠j)代表张量剪应变(1—2)其中u,v,w是在x,y,z方向的位移。
在方程(1—2)中,刚度矩阵Cij有30个常数.但是当考虑应变能时可以证明弹性材料的实际独立常数是少于36个的.存在有弹性位能或应变能密度函数的弹性材料当应力σi 作用于应变dεj时,单位体积的功的增量为:(1—3)由应力—应变关系式(1—1),功的增量为:(1—4)沿整个应变积分,单位体积的功为:(1—5)虎克定律关系式(1—1)可由方程(1—5)导出:(1—6)于是(1—7)同样(1—8)因W的微分与次序无,所以:(1—9)这样刚度矩阵是对称的且只有21个常数是独立的。
用同样的方法我们可以证明:(1—10)其中S是柔度矩阵,可由反演应力—变关系式来确定应变应力关系式为ij(1—11)同理(1—12)即柔度矩阵是对称的,也只有21个独立常数.刚度和柔度分量可认为是弹性常数。
在线性弹性范围内,应力—应变关系的一般表达式为:(1—13)实际上,关系式(1—13)是表征各向异性材料的,因为材料性能没有对称平面.这种各向异性材料的别名是全不对称材料.比各向异性材料有更多的性能对称性的材料将在下面几段中叙述.各种材料性能对称的应力—应变关系式的证明由蔡(Tais)等给出。
如果材料有一个性能对称平面应力—应变关系式可简化为(1—14)对称平是z=0.这种材料称为单对称材料.单对称材料有13个独立的弹性常数。

工程力学(静力学与材料力学)习题解答第17章 复合材料的力学行为17-1 图示结构中,两种材料的弹性模量分别为E a 和E b ,且已知E a >E b ,二杆的横截面面积均为bh ,长度为l ,两轮之间的间距为a ,试求: 1.二杆横截面上的正应力;2.杆的总伸长量及复合弹性模量;3.各轮所受的力。
知识点:静不定问题,复合弹性模量 难度:很难 解答:解:1.P Nb Na F F F =+ (1) b a l l ∆=∆ (2) bhE lF l a Na a =∆ (3) bhE lF l b b Nb =∆ (4)将(3)、(4)代入(2),得bNba Na E F E F =(5)(1)、(5)联立解得P b a a Na F E E E F +=,P b a bNb F E E E F +=bh F E E E bh F P b a a Na a +==σ,bh F E E E bh F Pb a b Nb b +==σ2.由(3)式 bhE E lF bh E l F l )(b a P a Na a +==∆ 设复合弹性模量E c)2(c P bh E lF l =∆,由于a l l ∆=∆,比较两式得2ba c E E E +=3.由于F Na >F Nb ,所以,轮C 、轮G 脱离接触面,所以受力为零。
0)(=∑F k M ,022R Nb Na =--a F hF h F H∴ b a b a P R 2E E E E a h F F H +-=,ba ba P R R 2E E E E a h F F F H D +-==17-2 玻璃纤维/环氧树脂单层复合材料由2.5kg 纤维与5kg 树脂组成。
已知玻璃纤维的弹性模量E f =85GPa ,密度f ρ= 2500kg/m 3,环氧树脂的弹性模量E m = 5GPa ,密度m ρ= 1200kg/m 3。
试求垂直于纤维方向和平行于纤维方向的弹性模量E y 和E x 。


复合材料力学答案【篇一:材料力学】教程第二版 pdf格式下载单辉祖主编本书是单辉祖主编《材料力学教程》的第2版。
是根据高等工业院校《材料力学教学基本要求》修订而成。
可作为一般高等工业院校中、少学时类材料力学课程的教材,也可作为多学时类材料力学课程基本部分的教材,还可供有关工程技术人员参考。
内容简介回到顶部↑本教村是普通高等教育“十五”国家级规划教材。
. 本教材仍保持第一版模块式的特点,由《材料力学(Ⅰ)》与《材料力学(Ⅱ)》两部分组成。
《材料力学(Ⅰ)》包括材料力学的基本部分,涉及杆件变形的基本形式与组合形式,涵盖强度、刚度与稳定性问题。
《材料力学(Ⅱ)》包括材料力学的加深与扩展部分。
本书为《材料力学(Ⅱ)》,包括非对称弯曲与特殊梁能量法(二)、能量法(二)、静不定问题分析、杆与杆系分析的计算机方法、应力分析的实验方法、疲劳与断裂以及考虑材料塑性的强度计算等八章。
各章均附有复匀题与习题,个别章还安排了利用计算机解题的作业。
..与第一版相同,本教材具有论述严谨、文字精炼、重视基础与应用、重视学生能力培养、专业面宽与教学适用性强等特点,而且,在选材与论述上,特别注意与近代力学的发展相适应。
本教材可作为高等学校工科本科多学时类材料力学课程教材,也可供高职高专、成人高校师生以及工程技术人员参考。
以本教材为主教材的相关教学资源,尚有《材料力学课堂教学多媒体课件与教学参考》、《材料力学学习指导书》、《材料力学网上作业与查询系统》与《材料力学网络课程》等。
...作译者回到顶部↑本书提供作译者介绍单辉祖,北京航空航天大学教。
1953年毕业于华东航空学院飞机结构专业,1954年在北京航空学院飞机结构专业研究生班学习。
1992—1993年,在美国特拉华大学复合材料中心.从事合作研究。
.历任教育部工科力学教材编审委员、国家教委工科力学课程指导委员会委员、中国力学学会教育工作委员会副主任委员、北京航空航天大学校务委员会委员、校学科评审组成员与校教学指导委员会委员等。
实验1 环氧树脂的环氧值测定一、实验目的掌握分析环氧树脂环氧值的方法。
二、实验原理环氧值E 定义为100g 环氧树脂中环氧基团物质的量(摩尔数)。
基于0.1mol 高氯酸标准滴定液与溴化四乙铵作用所生成的初生态溴化氢同环氧基的反应。
使用结晶紫作指示剂,或对于深色产物使用电位滴定法测定终点。
其化学反应方程式为()()HBr NClO H C HClO NBr H C +→+44524452 OH Br CH CH 2HBr +CH 2CH一旦高氯酸过量则HBr 就过量。
由空白实验与试样所耗高氯酸的差值计算样品的环氧值。
该方法的缺点是不适用于含氮元素的环氧树脂。
三、实验仪器和设备分析天平、滴定管等及必要的分析纯化学试剂。
四、实验步骤1、 取100ml 冰乙酸与0.1g 结晶紫溶解后作为滴定指示剂。
2、 取8.5ml 70%高氯酸水溶液加入1000ml 的容量瓶中,在加入 300ml 冰乙酸,摇匀后再加20ml 乙酸酐,最后以冰乙酸冲稀到刻度。
3、 标定高氯酸溶液。
称m 克邻苯二甲酸氢钾(分子质量204.22),用冰乙酸溶解,再用V 毫升高氯酸溶液滴定至显绿色终点,高氯酸浓度(单位:mol/L )为:22.2041000⨯=N V m 4、 取100g 溴化四乙铵溶于400ml 冰乙酸中,加几滴结晶紫指示剂于其中。
5、 称取环氧树脂0.5g 左右(精确至0.2mg )放入烧瓶中,加入10ml 三氯甲烷溶解,加入20ml 冰乙酸,再用移液管移10ml 溴化四乙铵溶液,立即用已标定了的高氯酸溶液滴定,由紫色变为稳定绿色为滴定终点。
记下所耗毫升数V 1和温度t 。
6、 同时并行取10ml 三氯甲烷、20ml 冰乙酸以及用移液管移10ml 溴化四乙铵溶液放入烧瓶中,立即用高氯酸滴定,同样由紫色变成稳定绿色为滴定终点。
记录所耗毫升数V 0(空白实验)。
7、 环氧值按下式计算:mN V V E 10)(01-=式中:m ——环氧树脂质量g; N ——高氯酸标准溶液浓度mol/L ;V 1、V 0——试样和空白试验所耗高氯酸体积ml ;8、 注意所用环氧树脂应不含氮元素。
复合材料力学试题答案判断题(正确的在括弧内划√,错误的在括弧内划×)。
1.“宏观力学”是在研究复合材料力学性能时,假定材料是均质的。
(√)2.单层是层合板的基本单元,在复合材料结构设计中又叫做三次结构。
(×)3.层合板由若干具体不同纤维方向的单层叠合而成,在复合材料机构设计中又叫二次结构。
(√)4.复合材料力学中,1为纵向,2为横向,应力规定拉为负,压为正。
(×)5.在单层板(正交各向异性)材料中,τ12不仅形成剪切变形,还存在剪拉耦合效应。
(×)6.在单层正交各向异性板中,11)1(11σεE =。
(√) 7.在单层正交各向异性板中,11122)1(2)2(221συσεεεE E -=+=。
(√) 8.单层板的工程弹性常数有5个,且相互独立。
(×)9.柔量矩阵{S}是对称矩阵,而模量举证{Q}不是对称矩阵。
(×)10.在正交单层板中,Q16=Q26=0,Q61=Q62,但其值不为零。
(×)11.在复合材料力学中,对于工程弹性常数存在如下关系:2121υυ=E E 。
(√) 12.在单层板偏轴刚度中,应力转换和应变转换关系式中,m=sin θ,n=cos θ。
(×)13. 在单层板偏轴刚度中,应力转换和应变转换关系式中存在如下关系:[][][]T T T 1-=σε。
(√)14.在ij Q 中,11Q 、22Q 是θ的偶函数,16Q 、26Q 也是θ的偶函数。
(×) 15.玻璃钢复合材料在拉伸时发生变形,所以是一种塑性材料。
(×)16.利用复合材料的强度准则,可以判断复合材料设计过程的安全性,同时可以计算极限载荷。
(×)17.利用最大应力准则判断材料安全性时,如果判断式大于1,说明材料的机构是安全的。
(×)18.在复合材料中,利用强度比可以计算复合材料的极限载荷。
(√)20.在对称层合板中,)()(z z --=θθ。
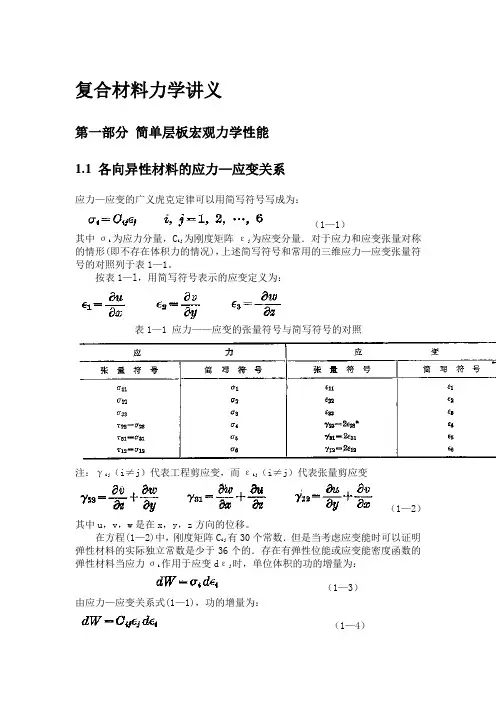
复合材料力学讲义
第一部分简单层板宏观力学性能
1.1各向异性材料的应力—应变关系
应力—应变的广义虎克定律可以用简写符号写成为:
(1—1)
其中σi为应力分量,C ij为刚度矩阵εj为应变分量.对于应力和应变张量对称的情形(即不存在体积力的情况),上述简写符号和常用的三维应力—应变张量符号的对照列于表1—1。
按表1—l,用简写符号表示的应变定义为:
表1—1 应力——应变的张量符号与简写符号的对照
注:γij(i≠j)代表工程剪应变,而εij(i≠j)代表张量剪应变
(1—2)其中u,v,w是在x,y,z方向的位移。
在方程(1—2)中,刚度矩阵C ij有30个常数.但是当考虑应变能时可以证明弹性材料的实际独立常数是少于36个的.存在有弹性位能或应变能密度函数的弹性材料当应力σi作用于应变dεj时,单位体积的功的增量为:
(1—3)
由应力—应变关系式(1—1),功的增量为:
(1—4)
沿整个应变积分,单位体积的功为:
(1—5)
虎克定律关系式(1—1)可由方程(1—5)导出:
(1—6)
于是
(1—7)
同样
(1—8)
因W的微分与次序无,所以:
(1—9)
这样刚度矩阵是对称的且只有21个常数是独立的。
用同样的方法我们可以证明:
(1—10)
其中S ij是柔度矩阵,可由反演应力—变关系式来确定应变应力关系式为
(1—11)
同理
(1—12)即柔度矩阵是对称的,也只有21个独立常数.刚度和柔度分量可认为是弹性常数。
在线性弹性范围内,应力—应变关系的一般表达式为:。