线性电阻电路分析

一、实验目的：
（1）学习线性电阻元件和非线性电阻元件伏安特性的测试方式。

（2）学习直流稳压电源、万用表、电压表的使用方法。

二、实验原理及说明
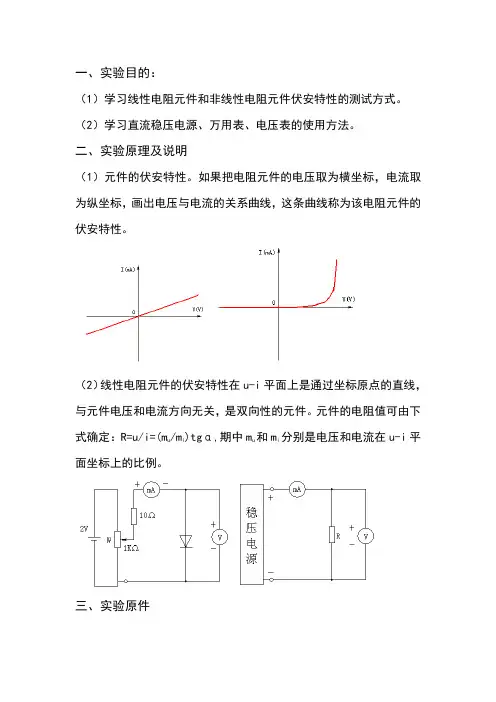
（1）元件的伏安特性。

如果把电阻元件的电压取为横坐标，电流取为纵坐标，画出电压与电流的关系曲线，这条曲线称为该电阻元件的伏安特性。

（2）线性电阻元件的伏安特性在u-i平面上是通过坐标原点的直线，与元件电压和电流方向无关，是双向性的元件。

元件的电阻值可由下式确定：R=u/i=(m u/m i)tgα,期中m u和m i分别是电压和电流在u-i平面坐标上的比例。

三、实验原件
U s是接电源端口，R1=120Ω,R2=51Ω,二极管D3为IN5404，电位器Rw
四、实验内容
（1）线性电阻元件的正向特性测量。

（2）反向特性测量。

（3）计算阻值，将结果记入表中
（4）测试非线性电阻元件D3的伏安特性
（5）测试非线性电阻元件的反向特性。

表1-1 线性电阻元件正（反）向特性测量
表1-5 二极管IN4007正（反）向特性测量
五、实验心得
（1）每次测量或测量后都要将稳压电源的输出电压跳回到零值（2）接线时一定要考虑正确使用导线。

线性电路的分析方法解析线性电路是由被动元件（如电阻、电容、电感等）和有源元件（如电源、放大器等）组成的一种电路。

线性电路主要通过应用基本电路定律和电路分析方法来分析和解决电路问题。

以下是常见的线性电路分析方法：1.基本电路定律：线性电路分析的基础是基本电路定律，包括欧姆定律（电流与电压成正比关系）、基尔霍夫电压定律（环路电压之和为0）和基尔霍夫电流定律（节点电流之和为0）。

通过这些定律可以建立电路的等式，进一步解决电路问题。

2.等效电路：将复杂的线性电路简化为等效电路是简化分析的常见方法。

等效电路可以用简单的电路元件（如电阻、电流源等）来代替原始电路，但仍然保持电路特性不变。

常见的等效电路包括电阻串联、并联、电流源串联和电压源并联等。

3.节点电压法：节点电压法是一种常用的线性电路分析方法。

它通过将电路中的节点连接到地（或任意选定基准点）上，使用基尔霍夫电流定律分析各节点的电压。

通过列写节点电压方程，可以解得节点的电压值，进而计算电路中的电流和功率等参数。

4.微分方程法：微分方程法是分析线性电路的另一种常见方法。

通过对电路中的元件进行建模，可以得到元件之间的基本关系式，进而得到描述电路行为的微分方程。

通过求解微分方程可以得到电路中的电流和电压等参数。

5.模拟计算：模拟计算是一种常用的线性电路分析方法。

通过使用模拟计算软件，将电路图输入并设置元件参数和初始条件，软件可以自动计算电路中的电流、电压和功率等参数，并绘制相应的波形图。

模拟计算可以方便地分析复杂的线性电路，并可以进行参数的优化和灵敏度分析。

6.相量法：对于交流电路，相量法是一种便捷的分析方法。

相量法将交流电压和电流看作有大小和相位的量，通过将它们用复数表示来进行分析。

通过相量法可以方便地计算交流电路中的电路参数，如电流、电压、功率等。

7.频域分析：频域分析是分析交流电路的另一种常用方法。

频域分析通过将电路中的电压和电流信号进行傅里叶变换，将它们从时域转换为频域。

线性电阻和非线性电阻实验报告线性电阻和非线性电阻实验报告引言：电阻是电路中常见的元件之一，它的作用是限制电流的流动。

在实际应用中，电阻可以分为线性电阻和非线性电阻两种类型。

本实验旨在通过实际测量和分析，探讨线性电阻和非线性电阻的特性和应用。

实验一：线性电阻特性测量1. 实验目的本实验旨在测量线性电阻的电流-电压特性曲线，并分析其特性。

2. 实验步骤（1）搭建线性电阻电路，将电流表和电压表连接到电路中。

（2）通过改变电源电压，记录不同电压下的电流值。

（3）根据测得的电流和电压值，绘制电流-电压特性曲线。

3. 实验结果与分析根据实验测量结果，我们绘制了线性电阻的电流-电压特性曲线。

从曲线可以看出，电流和电压之间呈现线性关系，符合欧姆定律。

线性电阻的电阻值可以通过曲线的斜率计算得出。

实验二：非线性电阻特性测量1. 实验目的本实验旨在测量非线性电阻的电流-电压特性曲线，并分析其特性。

2. 实验步骤（1）搭建非线性电阻电路，将电流表和电压表连接到电路中。

（2）通过改变电源电压，记录不同电压下的电流值。

（3）根据测得的电流和电压值，绘制电流-电压特性曲线。

3. 实验结果与分析根据实验测量结果，我们绘制了非线性电阻的电流-电压特性曲线。

与线性电阻不同，非线性电阻的电流-电压关系不是简单的线性关系。

在低电压范围内，电流随电压的增加而迅速增加，但随后增长速度逐渐减慢，形成曲线的饱和区域。

这是由于非线性电阻的电阻值随电压的改变而变化，导致电流-电压关系不再是线性的。

结论：通过本实验的测量和分析，我们深入了解了线性电阻和非线性电阻的特性和应用。

线性电阻的电流-电压关系呈现线性，符合欧姆定律；而非线性电阻的电流-电压关系则不是简单的线性关系，其电阻值随电压的改变而变化。

这些特性使得非线性电阻在电路设计和电子器件中具有广泛的应用，如温度传感器、光敏电阻等。

总结：通过本实验，我们不仅学习了线性电阻和非线性电阻的特性，还掌握了测量和分析电流-电压特性曲线的方法。

第二章 电阻电路的分析主要内容：定理法：叠加定理、替代定理、戴维南定理（诺顿定理）； 等效变换法：独立电源的等效变换、电阻的Y -Δ转换、移源法； 系统化法：节点电压法、回路电流法。

§2-1 线性电路的性质·叠加定理(superposition theorem)一、 线性电路的概念由线性元件及独立电源组成的电路。

电源的作用是激励，其它元件则是对电源的响应。

二、 线性电路的性质 1、齐次性： 若有图示的线性电路，在单电源激励下，以2R 的电流2i 为输出响应，则容易得到：s u R R R R R R R i 13322132++=由于321,,R R R 为常数，故有：s ku i =2显然，2i 与su 成比例。

在数学中，被称为“齐次性”，而在电路理论中则称为“比例性”。

2、相加性在图示的两激励电路中，若仍以2R 的电流2i 作为输出响应，则有：u+ |2us u+ ||2us s i R R R u R R i 2112121+++=显然，2i 由两项组成，第一项为电压源单独作用时，在电阻上引起的响应，每二项为电流源单独作用时，在电阻上引起的响应，每一项只与某个激励源成比例。

也即，由两个激励所产生的响应，表示为每一个激励单独作用时产生的响应之和。

这在数学中称为“相加性”，在电路理论中则称为“叠加性”。

三、 叠加定理在任何线性电阻电路中，每一元件的电流或电压都是电路中各个独立电源单独作用时在该元件产生的电流或电压的叠加。

叠加性是线性电路的一个根本属性。

注：叠加定理适用于线性电路。

在叠加的各分电路中，不作用的电压源置零（即，电压源用短路代替），不作用的电流源置零（即，电流源用开路代替），电阻不更动，受控源保留在各分电路中。

和分电路中的电压、电流的参考方向可以取为原电路中的相同方向，求和时，应注意各分量前的“+”、“-”号。

原电路的功率不等于按各分电路计算所得的功率叠加，这是因为功率是电压和电流的乘积。