高斯定理求电场E

静电场中的高斯定理：高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。

可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。

表达式为01()1/n i i S E ds q φε==∙=∑⎰⎰ （1）高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。

典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。

根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。

选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。

最后由高斯定理求出场强。

高斯定理说明的是通过闭合曲面的电通量与闭合曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。

但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。

下面举一些例子来说静电场中高定理的应用：例1：一半径为R 的带电球体，其电荷体密度分布为()Ar r R ρ=≤，0()r R ρ=>，A 为大于零的常量。

电场的高斯定理及其应用1. 高斯定理的背景高斯定理，也称为高斯电场定理，是电磁学中的基本定律之一。

它描述了电场通过任意闭合曲面的电通量与该闭合曲面内部的总电荷之间的关系。

这个定理是由德国数学家和物理学家卡尔·弗里德里希·高斯在19世纪初期提出的。

高斯定理在电磁学、物理学和工程学等领域有着广泛的应用。

2. 高斯定理的数学表述高斯定理的数学表述如下：对于任意闭合曲面S，电场通过S的电通量（记作ΦE）与曲面S内部的总电荷（记作q）之间存在以下关系：ΦE = ∫∫S E·dA = q / ε₀其中，E是电场强度，dA是曲面元素的面积向量，ε₀是真空的电介质常数（也称为电常数），其值约为8.85×10^-12 C2/N·m2。

3. 高斯定理的物理意义高斯定理的物理意义可以从两个方面来理解：（1）电场线与闭合曲面的关系：高斯定理说明，对于任意闭合曲面S，电场线通过S的电通量等于曲面S内部的总电荷。

这意味着，无论曲面S如何选择，只要它是闭合的，电场线穿过它的总通量都与曲面内部的电荷有关，而与曲面的形状和位置无关。

（2）电场的分布与电荷的关系：高斯定理表明，电场是通过闭合曲面的电通量的度量，而电通量与曲面内部的总电荷成正比。

这意味着，电场的强度和分布与曲面内部的电荷量有关，而与曲面的具体形状和位置无关。

4. 高斯定理的应用高斯定理在电场分析和计算中有着广泛的应用，下面列举几个常见的应用例子：（1）计算静电场中的电荷分布：通过高斯定理，可以计算静电场中某个闭合曲面内的电荷分布。

只需测量通过该曲面的电通量，然后根据电通量与电荷的关系，可以确定曲面内部的电荷量。

（2）设计电容器和绝缘材料：在电容器和绝缘材料的设计中，高斯定理可以用来分析电场的分布和电荷的积累。

通过合理选择闭合曲面的形状和位置，可以优化电场分布，提高电容器的性能和绝缘材料的可靠性。

（3）研究电磁波的传播：在研究电磁波的传播过程中，高斯定理可以用来分析电磁波在不同介质中的电场分布和电荷的变化。

有电介质时的高斯定理
有电介质时的高斯定理是电学中的一个重要定理，它描述了电场的分布与电荷分布的关系。

此定理的公式表述为：电场穿过一个封闭曲面的通量等于该曲面内部的电荷总量的比例，即ΦE=Q/ε0，其中ΦE为电场的通量，Q为曲面内部的电荷总量，ε0为真空中的电介质常数。

在有电介质时，电场的分布受到电介质的影响。

电介质的存在会使电场强度发生改变，这是因为电介质的分子会被电场极化，从而产生极化电荷。

这些极化电荷会改变电场的分布，使电场在电介质中的强度比在真空中的强度小。

因此，在有电介质时，要考虑电介质对电场的影响，才能准确地计算电荷的分布。

在应用高斯定理时，通常需要选择一个适当的曲面来计算电场的通量。

曲面的选择应当考虑到电荷分布的对称性，以便简化计算。

在有电介质时，曲面的选择也需要考虑到电介质的影响。

如果曲面穿过电介质，那么在计算电荷总量时，需要将电介质中的极化电荷也计算在内。

高斯定理的应用范围很广，包括电场的计算、电容器的设计、电荷分布的测量等。

在电场的计算中，高斯定理可以用来求解各种电场分布，例如电偶极子、均匀带电球面等。

在电容器的设计中，高斯定理可以用来计算电容器的电容量，从而确定电容器的电荷储存能
力。

在电荷分布的测量中，高斯定理可以用来测量电荷的总量，从而确定电荷的分布情况。

有电介质时的高斯定理是电学中的一个重要定理，它描述了电场的分布与电荷分布的关系。

在应用该定理时，需要考虑到电介质的影响，并选择适当的曲面来计算电场的通量。

高斯定理的应用范围很广，包括电场的计算、电容器的设计、电荷分布的测量等。

电磁场的高斯定律高斯定律是电磁学中非常重要的一个定律，它描述了与电荷和电场在空间分布有关的关系。

高斯定律由德国物理学家卡尔·弗里德里希·高斯在19世纪初发现和发表，被广泛应用于电磁学的研究和应用中。

高斯定律的表述是：电场通过一个闭合曲面的通量等于该闭合曲面内的总电荷除以真空介电常数。

这个定律用数学形式可以表示为：∮E·dA = Q/ε₀其中，∮E·dA表示电场E在某一个闭合曲面上的通量，Q表示该闭合曲面内的总电荷，ε₀表示真空介电常数。

高斯定律有着广泛的应用，下面将从静电场和静磁场两个方面来介绍高斯定律的应用。

一、静电场中的高斯定律静电场是指电荷不随时间变化的电场。

在静电场中，高斯定律可以简化为以下形式：一个闭合曲面上的电场通量等于该闭合曲面内的电荷除以真空介电常数。

利用高斯定律，我们可以推导出一些重要的结论。

比如，如果闭合曲面内没有电荷，那么该闭合曲面上的电场通量为零。

这是因为没有电荷产生的电场通过闭合曲面。

另外，如果闭合曲面内存在正电荷，那么该闭合曲面上的电场通量为正值；如果闭合曲面内存在负电荷，那么该闭合曲面上的电场通量为负值。

二、静磁场中的高斯定律在静磁场中，没有磁荷（单极子），因此高斯定律在磁场中不成立。

高斯定律只适用于描述与电荷和电场有关的情况。

但是在一些特殊情况下，我们可以利用高斯定律来计算磁场。

例如，考虑一个闭合的曲面，通过该曲面的磁场通量为Φ,那么根据高斯定律，磁场的通量Φ等于零。

这意味着，在静磁场中，磁场的通量是守恒的，即从一个闭合曲面的内部流出的磁场通量等于从该闭合曲面的外部流入的磁场通量。

结论高斯定律是描述电磁场中电荷和电场关系的重要定律。

它在静电场中的形式是电场通过闭合曲面的通量等于该闭合曲面内的总电荷除以真空介电常数。

它在静磁场中的形式可以用来说明磁场通量的守恒性质。

高斯定律的应用广泛，不仅可以用于解决静电场和静磁场中的问题，还可以扩展到动态的电磁场中。

电学高斯定理全文共四篇示例，供读者参考第一篇示例：电学高斯定理是电学领域中的重要定理之一，它描述了电场的性质与电荷之间的关系。

高斯定理的提出者是德国数学家卡尔·弗里德里希·高斯，他在通过对电场分析的基础上，发现了电场的一种非常有用的特性，这就是高斯定理。

电学高斯定理是电场理论的基石之一，它提供了一种简单而优雅的方法来计算静电场中的电荷分布和电场强度。

高斯定理描述了一个有无限小体积的闭合曲面，其内部电荷的总电量等于曲面上的电荷总和乘以一个常数，即真空介电常数乘以电场的通量。

高斯定理的数学形式如下：\[\oint\limits_S \vec{E} \cdot d\vec{A} =\frac{Q_{enc}}{\varepsilon_0}\]\(\oint\limits_S \vec{E} \cdot d\vec{A}\)表示电场强度在闭合曲面S上的通量，\(d\vec{A}\)表示曲面元素的面积微元，它与曲面的法线方向一致，\(Q_{enc}\)表示闭合曲面S内部的电荷总量，\(\varepsilon_0\)表示真空介电常数。

高斯定理的物理意义在于，它告诉我们，一个闭合曲面的电场通量只取决于曲面内部的电荷分布，与曲面的具体形状和大小无关。

这使得高斯定理成为了电场分布的计算利器，在许多问题的求解中起到了至关重要的作用。

举个简单的例子来说明高斯定理的应用。

假设我们有一个均匀带电的无限长线段，电荷密度为\(\lambda\)，现在我们希望确定距离这个线段距离为r处的电场强度。

我们可以选取一个半径为r的闭合球面，这个球面的中心位于线段上，利用高斯定理可以得到线段上的电荷等于球面包围电荷的总和，即：\[Q_{enc} = \lambda \cdot 2\pi r\]根据高斯定理，我们可以得到球面上的电场通量等于：如果我们假设球面上的电场强度与球面法线方向垂直，并且与球面上的法向面积元素大小相等，那么可以将上式简化为：解得电场强度为：这就是距离带电线段距离为r处的电场强度。

静电场的高斯定理引言静电场是指电荷在没有运动的情况下所形成的电场分布。

静电场的高斯定理是描述电场分布的一个重要定理，它由物理学家卡尔·弗里德里希·高斯在19世纪初提出。

高斯定理可以被用来计算任意闭合曲面内的电场强度，并且被广泛应用于电场的分析和解题中。

高斯定理的表述高斯定理的表述为：通过任意闭合曲面的电场通量等于该闭合曲面内部所包围电荷的总电量的1/ε0 倍，其中ε0为真空中的介电常数。

数学表达式为：∮E·dA = Q/ε0其中∮表示闭合曲面上的面积分，E为闭合曲面上的电场强度，dA为闭合曲面上的面积元素，Q为被闭合曲面包围的总电量。

高斯定理的表述说明了电场强度的分布与所包围电荷分布的关系，即闭合曲面上的电场通量与所包围电荷的性质直接相关。

高斯定理的证明高斯定理的证明可以通过以下几个步骤完成：1.假设存在一个闭合曲面，我们可以通过取一个小区域在曲面上，该小区域面积为dA。

假设该小区域上的电场强度为E，那么在该小区域上的电场通量为E·dA。

2.通过不断增大小区域的数量，将整个闭合曲面分成许多小区域，那么闭合曲面上的电场通量可以表示为所有小区域上电场通量的和。

3.由于电场可以穿过某些小区域而不通过闭合曲面，因此我们需要将穿过闭合曲面的电场通量作为负数计算。

这可以通过将某些小区域上的电场通量乘以-1来实现。

4.根据电场强度的定义，可以知道通过闭合曲面的电场通量与闭合曲面内部所包围的电荷有关。

因此，我们可以将电场通量表示为闭合曲面内电荷分布的函数。

5.结合步骤2和步骤3，我们可以将闭合曲面上的电场通量表示为闭合曲面内电荷分布的累加。

通过进一步的数学推导，最终可以得到高斯定理的数学表达式。

高斯定理的应用高斯定理在电场分析和解题中有着广泛的应用。

通过高斯定理，我们可以方便地计算出一个闭合曲面内部的电场强度。

一些常见的应用场景包括： 1. 计算均匀带电球壳内外的电场强度。

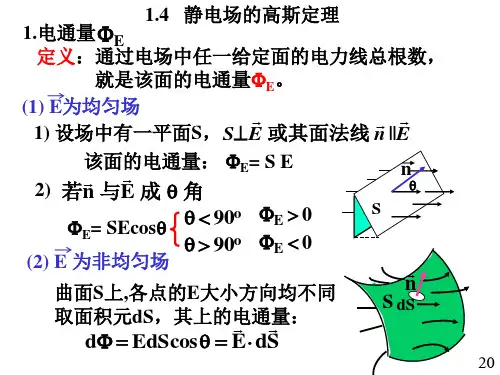
静电场中的高斯定理：高斯定理是静电学中的一个重要定理, 它反映了静电场的一个基本性质, 即静电场是有源场, 其源即是电荷。

可表述为: 在静电场中, 通过任意闭合曲面的电通量, 等于该闭合曲面所包围的电荷的代数和的1/ε倍, 与闭合曲面外的电荷无关。

表达式为01()1/ni i S E ds q φε==∙=∑⎰⎰ （1）高斯定理是用来求场强E 分布, 定理中, S 是任意曲面, 由于数学水平的限制, 要由高斯定理计算出E,则对由场的分布有一定的要求, 即电荷分布具有严格的对称性( 若电荷分布不对称性即不是均匀的, 引起电场分布不对称, 不能从高斯定理求空间场强分布,高斯定理当然仍是成立的) , 由于电荷分布的对称性导致场强分布的对称性, 场强分布的对称性应包括大小和方向两个方面。

典型情况有三种:1) 球对称性, 如点电荷, 均匀带电球面或球体等;2) 轴对称性, 如无限长均匀带电直线, 无限长均匀带电圆柱或圆柱面, 无限长均匀带电同轴圆柱面3) 面对称性, 如均匀带电无限大平面或平板,或者若干均匀带电无限大平行平面。

根据高斯定理计算场强时, 必须先根据电荷分布的对称性, 分析场强分布的对称性; 再适当选取无厚度的几何面作为高斯面。

选取的原则是:○1 待求场强的场点必须在高斯面上;○2 使高斯面的各个部分或者与E 垂直, 或者E 平行;○3 与E 垂直的那部分高斯面上各点的场强应相等;○4 高斯面的形状应是最简单的几何面。

最后由高斯定理求出场强。

高斯定理说明的是通过闭合曲面的电通量与闭合 曲面所包围的所有电荷的代数和之间的关系, 即闭合曲面的总场强E 的电通量只与曲面所包围的电荷有关, 但与曲面内电荷的分布无关。

但闭合曲面上的电场强度却是与曲面内外所有电荷相联系的,是共同激发的结果。

下面举一些例子来说静电场中高定理的应用：例1：一半径为R 的带电球体，其电荷体密度分布为()Ar r R ρ=≤，0()r R ρ=>，A 为大于零的常量。

静电场的高斯定理和环路定理
静电场是指电荷分布静止不动的情况下所产生的电场。

在静电场中，高斯定理和环路定理是两个非常重要的定理。

高斯定理是描述电场通量的定理，它表明：在任何闭合曲面内，电场的通量等于该曲面内的电荷总量除以介质常数。

即：ΦE = ∫E · dS = Q/ε0
其中，ΦE表示电场的通量，E表示电场强度，dS表示曲面元素的面积，Q表示该曲面内的电荷总量，ε0表示真空中的介电常数。

环路定理则是描述电场中电势的变化的定理，它表明：沿着任意闭合回路的线积分等于该回路内的电荷的代数和除以电容。

即：∮Edl = 0
其中，∮Edl表示沿着回路的电场强度的线积分，E表示电场强度，dl表示回路的微元长度，如果回路内有电荷则其代数和为Q。

电容则是电荷和电势之间的比值。

高斯定理和环路定理是静电学中的基本定理，对于研究静电场的性质和计算电场强度、电势等都具有重要的意义。

- 1 -。

关于电场的高斯定理高斯定律（gauss' law），属物理定律。

在静电场中，穿过任一封闭曲面的电场强度通量只与封闭曲面内的电荷的代数和有关，且等于封闭曲面的电荷的代数和除以真空中的电容率。

该定律表明在闭合曲面内的电荷分布与产生的电场之间的关系。

静电场中通过任意闭合曲面（称高斯面）s 的电通量等于该闭合面内全部电荷的代数和除以真空中的电容率，与面外的电荷无关。

物理定律由于磁力线总是闭合曲线，因此任何一条进入一个闭合曲面的磁力线必定会从曲面内部出来，否则这条磁力线就不会闭合起来了。

如果对于一个闭合曲面，定义向外为正法线的指向，则进入曲面的磁通量为负，出来的磁通量为正，那么就可以得到通过一个闭合曲面的总磁通量为0。

这个规律类似于电场中的高斯定理，因此也称为高斯定理。

与静电场中的高斯定理相比较，两者有著本质上的区别。

在静电场中，由于自然界中存有着单一制的电荷，所以电场线存有起点和终点，只要闭合面内有净余的也已（或负）电荷，沿着闭合面的电通量就不等于零，即为静电场就是有源场；而在磁场中，由于自然界中没单独的磁极存有，n极和s极就是无法拆分的，磁感线都就是无头无尾的滑动线，所以通过任何闭合面的磁通量必等于零。

特别要强调两点： 1.关于电场线的方向的规定：电场线上每一点的切线方向就是该点电场的方向。

2.关于电场线的疏密的规定：电场线在某处的疏密要反映电场强度的大小，即在电场中通过某一点的电场线的数密度与该点电场强度的大小呈正相关，即： e=dn/ds，其中ds是在电场中的某一点取一个通过该点的且与电场线垂直的微分面，dn就是穿过该面ds的电场线的根数。

高斯定理来源于库仑定律,依赖场强共振原理,只有当电场线密度等同于场强悍小时场线通量就可以与场强通量等同于,并统一遵守高斯定理。

高斯面上的实际场强就是其内外所有电荷产生的场强共振而变成的合场强。

但利用高斯面所求出的场强则仅仅就是分析高斯面上场强原产时所牵涉的电荷在高斯面上产生的合场强,而不涵盖未牵涉的电荷所产生的场强。

电场中的高斯定律与电容器电场是物理学中重要而广泛研究的一个概念，它描述了电荷之间相互作用的力以及它们引起的电场。

而高斯定律是描述电场分布的一条基本规律。

本文将介绍高斯定律的原理以及它在电场中的应用，以及电容器在电路中的作用。

一、高斯定律的原理高斯定律是由德国物理学家卡尔·弗里德里希·高斯于19世纪初提出的。

它表明，电场通过一个闭合曲面的通量正比于该曲面内的电荷总量。

具体来说，高斯定律可以用如下公式表示：Φ = ε0 * Q其中，Φ表示通过闭合曲面的电场通量，ε0是真空介电常数，Q是该曲面内的电荷总量。

这个定律适用于静电场，即电荷不发生变化的情况。

二、高斯定律在电场中的应用高斯定律在电场中的应用非常广泛。

下面将介绍两个典型的应用情况。

1. 对称电场中的高斯定律在一些特殊情况下，电场具有对称性，此时可以利用高斯定律简化计算。

例如，对于一个球形电荷分布，以球心为原点建立球坐标系，可以通过高斯定律来计算球外的电场强度。

根据高斯定律，球外任意一点的电场通量只与球内电荷总量有关，与球外的分布无关。

因为球形电荷分布具有球对称性，所以球外的电场强度与距离r的关系可以简化为：E = k * Q / r²其中，E表示电场强度，k为电场常数，Q为球内电荷总量，r为球外点到球心的距离。

2. 无限大带电平面的高斯定律另一个常见的应用情况是对于无限大带电平面的电场计算。

假设有一无限大的平面带上均匀分布了电荷密度σ，我们要求该平面上任意点的电场强度。

将平面设为xy平面，带电平面位于z=0处，选取z轴垂直平面向上为正方向。

对于高斯面，可以选取一个与带电平面平行的、与之距离为d的平面作为高斯面，这样在该高斯面上的电场强度垂直于面积。

根据高斯定律，可以得到：E * A = ε0 * σ * A其中E表示电场强度，A表示高斯面的面积，ε0为真空介电常数，σ为带电平面的电荷密度。

由于高斯面上的电场强度是常数，所以电场强度与高斯面面积的比例为常数，这样带电平面上任意点的电场强度为：E = σ / (2 * ε0)三、电容器在电路中的作用除了高斯定律，电容器也是电学中的重要概念。

高斯定理物理表达式
高斯定理是物理学中一项重要的基础定理，也被称为高斯通量定理。

该定理表达了电场、磁场等物理场在闭合曲面内外的通量之间的关系。

以下是高斯定理的物理表达式以及相关概念的解释：
1. 高斯定理的物理表达式：
高斯定理的物理表达式可以用数学公式表示为：
∮S E·dA = Q/ε0，其中∮S表示对闭合曲面S所围体积的积分，E表示
电场强度，dA表示面积微元，Q表示闭合曲面内固定的电荷总量，ε0
表示真空中的介电常数。

2. 闭合曲面的概念：
闭合曲面是一个在三维空间中完全封闭的曲面，可以看成是由许多面
积微元组成的。

高斯定理是针对闭合曲面内外的物理场通量之间的关
系而言的。

3. 电场强度：
电场强度是指在任意一点处，单位电荷所受的电力的大小和方向。

在
高斯定理中，电场强度是重要的物理量之一，用来衡量电场的强度和方向。

4. 电荷总量：
电荷总量指的是一个闭合曲面内的所有电荷的代数和，可以是正的、负的或零，也可以是分布式电荷或点电荷。

5. 真空中介电常数：
真空中的介电常数是一个比例系数，用于描述真空中电场强度与电荷密度之间的关系。

在高斯定理中，介电常数是一个常量，用来计算电荷总量与电场强度之间的关系。

6. 高斯定理的意义：
高斯定理是重要的物理学原理之一，对于电场、磁场等物理场的研究有着重要的意义。

它可以帮助我们更好地理解、描述和计算物理场的性质和变化规律，特别是在电场强度和电荷分布较为复杂的情况下，能够简化计算过程。

同时，高斯定理也为物理学中的其他定理和理论提供了重要的基础。

高斯定理求电场强度的条件1. 引言大家好，今天我们来聊聊高斯定理，听起来可能有点高大上，但其实它就像我们日常生活中的一块小拼图，懂了它，电场的秘密就都在你掌握之中了。

高斯定理告诉我们，如何通过一些简单的条件来求出电场强度，就像开窍一样，瞬间明了！所以，咱们就从这里开始，慢慢深入，最终达到“运筹帷幄”的境地。

2. 高斯定理的基础2.1 定义首先，高斯定理是关于电场与电荷之间关系的一个重要定理。

简而言之，它告诉我们，封闭表面内的电通量与这个表面包围的电荷总量成正比。

这么说吧，就像你在派对上，空气中充满了欢乐的气氛，而这气氛的浓烈程度正好取决于派对上有多少人。

人多，气氛就火爆；人少，气氛就冷清。

这就是高斯定理的道理！2.2 应用场景这一定理在很多场景中都能派上用场，比如说求取均匀带电球体、平面电荷分布等等。

要是你碰上这种情况，简直就像找到了一把打开宝藏的钥匙，轻松又方便。

不过，咱们得先满足一些条件，才能顺利使用这把钥匙，接下来就让我们看看那些“门槛”吧。

3. 求电场强度的条件3.1 对称性首先，咱们得考虑对称性。

高斯定理最适合在高度对称的情况下使用，比如球对称、柱对称或平面对称。

如果你拿到的电场情况就像是一团乱麻，啥对称性都没有，那就真的“无从下手”了！所以，找到电场的对称性，像是找到了一个指南针，让你在复杂的电场中不至于迷失方向。

3.2 封闭表面的选择其次，选择一个合适的封闭表面也是至关重要的。

这个封闭面必须能够很好地包围电荷，这就像我们在选择一个适合的容器装食物一样，得确保容器的形状和大小能把食物完全包裹住。

比如说，面对一个均匀带电的球体，你可以选择一个同心球面作为封闭面，这样就能轻松算出电场强度。

如果选择的封闭面不合适，结果就会跟“东施效颦”一样，搞得一团糟。

4. 计算电场强度4.1 公式应用好了，条件都满足了，接下来就是计算电场强度了。

根据高斯定理，电场强度的计算公式为：电场强度E=Q/ε₀·S。