下载文档原格式
3 第四章弯曲内力一、教学目标和教学内容1、教学目标⑴掌握弯曲变形与平面弯曲等基本概念；⑵熟练掌握用截面法求弯曲内力；⑶熟练列出剪力方程和弯矩方程并绘制剪力图和弯矩图；⑷利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图；⑸掌握叠加法绘制剪力图和弯矩图。
2教学内容⑴平面弯曲等基本概念；⑵截面法及简便方法求弯曲内力；⑶剪力方程和弯矩方程、绘制剪力图和弯矩图；⑷用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯矩图；⑸叠加法绘制剪力图和弯矩图。
二．重点难点1、平面弯曲的概念；2、剪力和弯矩，剪力和弯矩的正负符号规则；3、剪力图和弯矩图；4、剪力、弯矩和载荷集度的微分、积分关系；5、叠加法绘制剪力图和弯矩图。
讲课提纲§4.1 弯曲的概念和实例§4.2 受弯杆件的简化§4.5 载荷集度、剪力和弯矩之间的关系§4.3 剪力和弯矩§4.4 剪力方程和弯矩方程剪力图和弯矩图F §4.6 平面曲杆的弯曲内力§4.1 弯曲的概念和实例1.实例(1)桥式起重机大梁（2）火车轮轴（3）镗刀刀杆（4）轧板机的轧辊2.弯曲变形作用于杆件上垂直于杆件轴线，使原为直线的轴线变成曲线，这种变形成为弯曲变形。
梁——凡以弯曲变形为主的杆件，习惯上称为梁。
对称弯曲（1）横截面有一根对称轴（2）整个杆件有一包含对称轴的纵向对称截面（3）所有外力都作用在纵向截面内（4）弯曲变形后轴线变成纵向截面内的一条平面曲线§ 4.2 受弯杆件的简化根据支座和载荷简化，最后可以的到梁的计算简化图，计算简化图以梁的轴线和支承来表示梁。
⎪⎩⎪⎨⎧）悬臂梁（）外伸梁（简支梁32)1(三种梁的基本形式 （1）简支梁(2)外伸梁(3)悬臂梁↑↑FFBFA↓BA↑↑AB↓FAFBFy xF F F F ←纵截面↓对称轴↓F§4.3 剪力和弯矩 （1）求支反力∑M A =0 ∑M B =0 (2)求内力（截面法）一般截面上有剪力F s 和弯矩M ，一截面一侧为研究对象列平衡方程就可以计算出剪力和弯矩。
第十一讲内容一 用内力方程法绘制剪力图和弯矩图为了计算梁的强度和刚度问题，除了要计算指定截面的剪力和弯矩外，还必须知道剪力和弯矩沿梁轴线的变化规律，从而找到梁内剪力和弯矩的最大值以及它们所在的截面位置。
(一)、剪力方程和弯矩方程从上节的讨论可以看出，梁内各截面上的剪力和弯矩一般随截面的位置而变化的。
若横截面的位置用沿梁轴线的坐标x 来表示，则各横截面上的剪力和弯矩都可以表示为坐标x 的函数，即)(x Q Q =， )(x M M =以上两个函数式表示梁内剪力和弯矩沿梁轴线的变化规律，分别称为剪力方程和弯矩方程。
(二)、剪力图和弯矩图为了形象地表示剪力和弯矩沿梁轴线的变化规律，可以根据剪力方程和弯矩方程分别绘制剪力图和弯矩图。
以沿梁轴线的横坐标x 表示梁横截面的位置，以纵坐标表示相应横截面上的剪力或弯矩，在土建工程中，习惯上把正剪力画在x 轴上方，负剪力画在x 轴下方；而把弯矩图画在梁受拉的一侧，即正弯矩画在x 轴下方，图。
【解】（1）求支座反力 因对称关系，可得ql R R 21B A == (↑)(2)列剪力方程和弯矩方程取距A 点为x 处的任意截面，将梁假想截开，考虑左段平衡，可得(a )(b ) (c )图9-13 例9-4图)0( 21)(A l x qx ql qx R x Q <<-=-= (1) )0( 212121)(22A l x qx qlx qx x R x M ≤≤-=-= (2)(3)画剪力图和弯矩图由式(1)可见，)(x Q 是x 的一次函数，即剪力方程为一直线方程，剪力图是一条斜直线。
当 0=x 时2A qlQ =l x = 时 2B qlQ -=根据这两个截面的剪力值，画出剪力图，如图9-13b 所示。
由式(2)知，Ｍ(x )是x 的二次函数，说明弯矩图是一条二次抛物线，应至少计算三个截面的弯矩值,才可描绘出曲线的大致形状。
当 0=x 时， 0A =M2lx = 时， 82C ql M =l x = 时， 0B =M根据以上计算结果，画出弯矩图，如图9-13c 所示。
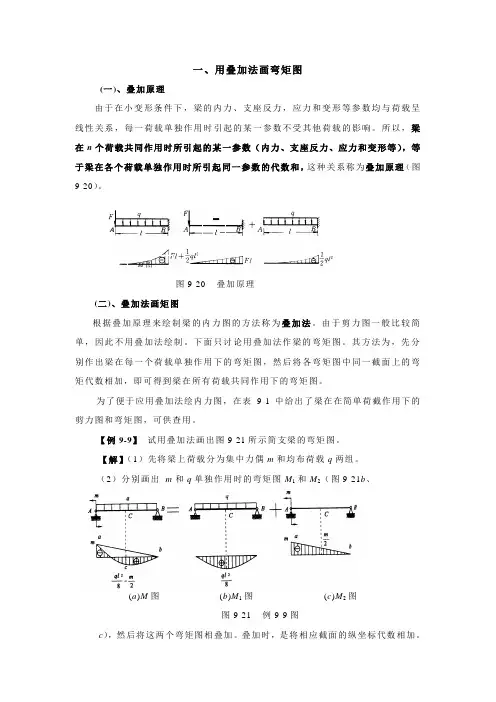
一、用叠加法画弯矩图(一)、叠加原理由于在小变形条件下，梁的内力、支座反力，应力和变形等参数均与荷载呈线性关系，每一荷载单独作用时引起的某一参数不受其他荷载的影响。
所以，梁在n个荷载共同作用时所引起的某一参数（内力、支座反力、应力和变形等），等于梁在各个荷载单独作用时所引起同一参数的代数和，这种关系称为叠加原理（图9-20）。
=M图图9-20 叠加原理(二)、叠加法画矩图根据叠加原理来绘制梁的内力图的方法称为叠加法。
由于剪力图一般比较简单，因此不用叠加法绘制。
下面只讨论用叠加法作梁的弯矩图。
其方法为，先分别作出梁在每一个荷载单独作用下的弯矩图，然后将各弯矩图中同一截面上的弯矩代数相加，即可得到梁在所有荷载共同作用下的弯矩图。
为了便于应用叠加法绘内力图，在表9-1中给出了梁在在简单荷截作用下的剪力图和弯矩图，可供查用。
【例9-9】试用叠加法画出图9-21所示简支梁的弯矩图。
【解】（1）先将梁上荷载分为集中力偶m和均布荷载q两组。
（2）分别画出m和q单独作用时的弯矩图M1和M2（图9-21b、(a)M图(b)M1图(c)M2图图9-21 例9-9图c），然后将这两个弯矩图相叠加。
叠加时，是将相应截面的纵坐标代数相加。
叠加方法如图9-21a 所示。
先作出直线形的弯矩图M 1（即ab 直线，可用虚线画出），再以ab 为基准线作出曲线形的弯矩图M 2 。
这样，将两个弯矩图相应纵坐标代数相加后，就得到m 和q 共同作用下的最后弯矩图M （图9-21a ）。
其控制截面为A 、B 、C 。
即A 截面弯矩为 ：m m M -=+-=0A ，B 截面弯矩为 ：000B =+=M跨中C 截面弯矩为：282C mql M -= 叠加时宜先画直线形的弯矩图，再叠加上曲线形或折线形的弯矩图。
由上例可知，用叠加法作弯矩图，一般不能直接求出最大弯矩的精确值，若需要确定最大弯矩的精确值，应找出剪力Q =0的截面位置，求出该截面的弯矩，即得到最大弯矩的精确值。
第十一讲内容一 用内力方程法绘制剪力图和弯矩图为了计算梁的强度和刚度问题，除了要计算指定截面的剪力和弯矩外，还必须知道剪力和弯矩沿梁轴线的变化规律，从而找到梁内剪力和弯矩的最大值以及它们所在的截面位置。
(一)、剪力方程和弯矩方程从上节的讨论可以看出，梁内各截面上的剪力和弯矩一般随截面的位置而变化的。
若横截面的位置用沿梁轴线的坐标x 来表示，则各横截面上的剪力和弯矩都可以表示为坐标x 的函数，即)(x Q Q =， )(x M M =以上两个函数式表示梁内剪力和弯矩沿梁轴线的变化规律，分别称为剪力方程和弯矩方程。
(二)、剪力图和弯矩图为了形象地表示剪力和弯矩沿梁轴线的变化规律，可以根据剪力方程和弯矩方程分别绘制剪力图和弯矩图。
以沿梁轴线的横坐标x 表示梁横截面的位置，以纵坐标表示相应横截面上的剪力或弯矩，在土建工程中，习惯上把正剪力画在x 轴上方，负剪力画在x 轴下方；而把弯矩图画在梁受拉的一侧，即正弯矩画在x 轴下方，图。
【解】（1）求支座反力 因对称关系，可得ql R R 21B A == (↑)(2)列剪力方程和弯矩方程取距A 点为x 处的任意截面，将梁假想截开，考虑左段平衡，可得(a )(b ) (c )图9-13 例9-4图)0( 21)(A l x qx ql qx R x Q <<-=-= (1) )0( 212121)(22A l x qx qlx qx x R x M ≤≤-=-= (2)(3)画剪力图和弯矩图由式(1)可见，)(x Q 是x 的一次函数，即剪力方程为一直线方程，剪力图是一条斜直线。
当 0=x 时2A qlQ =l x = 时 2B qlQ -=根据这两个截面的剪力值，画出剪力图，如图9-13b 所示。
由式(2)知，Ｍ(x )是x 的二次函数，说明弯矩图是一条二次抛物线，应至少计算三个截面的弯矩值,才可描绘出曲线的大致形状。
当 0=x 时， 0A =M2lx = 时， 82C ql M =l x = 时， 0B =M根据以上计算结果，画出弯矩图，如图9-13c 所示。
从剪力图和弯矩图中可知，受均布荷载作用的简支梁，其剪力图为斜直线，弯矩图为二次抛物线；最大剪力发生在两端支座处，绝对值为ql Q 21max=；而最大弯矩发生在剪力为零的跨中截面上，其绝对值为2max81ql M=。
结论：在均布荷载作用的梁段，剪力图为斜直线，弯矩图为二次抛物线。
在剪力等于零的截面上弯矩有极值。
【例9-5】 简支梁受集中力作用如图9-14a 所示，试画出梁的剪力图和弯矩图。
【解】(1)求支座反力 由梁的整体平衡条件0B =∑M ， l FbR =A (↑) 0A =∑M ， lFaR =B (↑)校核： 0B A =-+=-+=∑F lFal Fb F R R Y计算无误。
(2)列剪力方程和弯矩方程梁在C 处有集中力作用，故AC 段和CB 段的剪力方程和弯矩方程不相同，要 分段列出。
(a )(b )(c )图9-14 例9-5图AC 段：距A 端为x 1的任意截面处将梁假想截开，并考虑左段梁平衡，列出剪力方程和弯矩方程为)(0 )(1A 1a x l FbR x Q <<== (1) )0( )(111A 1a x x lFbx R x M ≤≤== (2)CB 段：距A 端为x 2 的任意截面外假想截开，并考虑左段的平衡，列出剪力方程和弯矩方程为)( )(2A 2l x a lFaF l Fb F R x Q <<-=-=-= (3) )( )()()(2222A 2l x a x l lFaa x F x R x M ≤≤-=--= (4)(3)画剪力图和弯矩图根据剪力方程和弯矩方程画剪力图和弯矩图。
Q 图：AC 段剪力方程Q (x 1)为常数，其剪力值为lFb，剪力图是一条平行于x 轴的直线，且在x 轴上方。
CB 段剪力方程Q(x 2)也为常数，其剪力值为lFa-，剪力图也是一条平行于x 轴的直线，但在x 轴下方。
画出全梁的剪力图，如图9-14b 所示。
M 图：AC 段弯矩M (x 1)是x 1的一次函数，弯矩图是一条斜直线，只要计算两个截面的弯矩值，就可以画出弯矩图。
当 01=x 时 0A =Ma x =1 时 lFabM =C 根据计算结果，可画出AC 段弯矩图。
CB 段弯矩M (x 2)也是x 2的一次函数，弯矩图仍是一条斜直线。
当 a x =2 时 lFabM =C l x =2 时 0B =M由上面两个弯矩值，画出CB 段弯矩图。
整梁的弯矩图如图9-14c 所示。
从剪力图和弯矩图中可见，简支梁受集中荷载作用，当 a >b 时，lFaQ =max ，发生在BC 段的任意截面上；lFabM =max，发生在集中力作用处的截面上。
若集中力作用在梁的跨中，则最大弯矩发生在梁的跨中截面上，其值为：4max Fl M =。
结论：在无荷载梁段剪力图为平行线，弯矩图为斜直线。
在集中力作用处，左右截面上的剪力图发生突变，其突变值等于该集中力的大小，突变方向与该集中力的方向一致；而弯矩图出现转折，即出现尖点，尖点方向与该集中力方向一致。
【例9-6】 如图9-15a 所示简支梁受集中力偶作用，试画出梁的剪力图和弯矩图。
【解】(1)求支座反力由整梁平衡得 (a ),0B =∑M l mR =A （↑） ,0A =∑M lmR -=B （↓）校核：0B A =-=+=∑lm l m R R Y 计算无误。
(b ) （2）列剪力方程和弯矩方程在梁的Ｃ截面的集中力偶m 作用，分两段列出剪力方程和弯矩方程。
(c )AC 段：在 A 端为x 1的截面处假想将梁截开，考虑左段梁平衡， 图9-15 例9-6图 列出剪力方程和弯矩方程为)0( )(1A 1a x l mR x Q ≤<== （1） )0( )(111A 1a x x lmx R x M <≤== （2）CB 段：在 A 端为x 2的截面处假想将梁截开，考虑左段梁平衡，列出剪力方程和弯矩方程为)( )(2A 2l x a lmR x Q <≤== (3) )( )()(222A 2l x a x l lmm x R x M ≤<--=-= (4)(3)画剪力图和弯矩图Q 图：由式（1）、（3）可知，梁在AC 段和CB 段剪力都是常数，其值为lm，故剪力是一条在x 轴上方且平行于x 轴的直线。
画出剪力图如图9-15 b 所示。
M 图：由式（2）、（4）可知，梁在AC 段和CB 段内弯矩都是x 的一次函数，故弯矩图是两段斜直线。
AC 段：当01=x 时， 0A =Ma x =1时， l maM =C 左 CB 段：当a x =2时， lmbM -=2右 当l x =2 时， 0B =M画出弯矩图如图9-15c 所示。
由内力图可见，简支梁只受一个力偶作用时，剪力图为同一条平行线，而弯矩图是两段平行的斜直线，在集中力偶处左右截面上的弯矩发生了突变。
结论：梁在集中力偶作用处，左右截面上的剪力无变化，而弯矩出现突变，其突变值等于该集中力偶矩。
二、 微分关系法绘制剪力图和弯矩图 (一)、荷载集度、剪力和弯矩之间的微分关系上一节从直观上总结出剪力图、弯矩图的一些规律和特点。
现进一步讨论剪力图、弯矩图与荷载集度之间的关系。
如图9-16a 所示，梁上作用有任意的分布荷载)(x q ，设)(x q 以向上为正。
取A 为坐标原点， x 轴以向右为正。
现取分布荷载作用下的一微段d x 来研究(图9-16b )。
(a ) (b )图9-16 荷载与内力的微分关系由于微段的长度d x 非常小，因此，在微段上作用的分布荷载)(x q 可以认为是均布的。
微段左侧横截面上的剪力是)(x Q 、弯矩是)(x M ；微段右侧截面上的剪力是)(d )(x Q x Q +、弯矩是)(d )(x M x M +，并设它们都为正值。
考虑微段的平衡，由0=∑Y 0)](d )([d )()(=+-+x Q x Q x x q x Q得)(d )(d x q xx Q = （9-1） 结论一：梁上任意一横载面上的剪力对x 的一阶导数等于作用在该截面处的分布荷载集度。
这一微分关系的几何意义是，剪力图上某点切线的斜率等于相应截面处的分布荷载集度。
再由0c =∑M 0)](d )([2d d )(d )()(=++---x M x M xxx q x x Q x M 上式中，Ｃ点为右侧横截面的形心， 经过整理，并略去二阶微量2d )(2x x q 后，得)(d )(d x Q xx M = （9-2） 结论二：梁上任一横截面上的弯矩对x 的一阶导数等于该截面上的剪力。
这一微分关系的几何意义是，弯矩图上某点切线的斜率等于相应截面上剪力。
将式（9-2）两边求导，可得)(d )(d 22x q x x M = （9-3） 结论三：梁上任一横截面上的弯矩对x 的二阶导数等于该截面处的分布荷载集度。
这一微分关系的几何意义是，弯矩图上某点的曲率等于相应截面处的荷载集度，即由分布荷载集度的正负可以确定弯矩图的凹凸方向。
(二)、用微分关系法绘制剪力图和弯矩图利用弯矩、剪力与荷载集度之间的微分关系及其几何意义。
可总结出下列一些规律，以用来校核或绘制梁的剪力图和弯矩图。
1．在无荷载梁段，即0)(=x q 时由式(9-1)可知，)(x Q 是常数，即剪力图是一条平行于x 轴的直线；又由式(9-2)可知该段弯矩图上各点切线的斜率为常数，因此，弯矩图是一条斜直线。
2．均布荷载梁段，即=)(x q 常数时由式(9-1)可知，剪力图上各点切线的斜率为常数，即)(x Q 是x 的一次函数，剪力图是一条斜直线；又由式(9-2)可知，该段弯矩图上各点切线的斜率为x 的一次函数，因此，)(x M 是x 的二次函数，即弯矩图为二次抛物线。
这时可能出现两种情况，如图9-17所示。
)(0↓<q )(0↑>q M M图9-17 M 图的凹凸向与q (x )的关系3．弯矩的极值 由0)(d )(d ==x Q xx M 可知，在0)(=x Q 的截面处，)(x M 具有极值。
即剪力等于零的截面上，弯矩具有极值；反之，弯矩具有极值的截面上，剪力一定等于零。
利用上述荷载、剪力和弯矩之间的微分关系及规律，可更简捷地绘制梁的剪力图和弯矩图，其步骤如下：（1）分段，即根据梁上外力及支承等情况将梁分成若干段；（2）根据各段梁上的荷载情况，判断其剪力图和弯矩图的大致形状； （3）利用计算内力的简便方法，直接求出若干控制截面上的Q 值和M 值； （4）逐段直接绘出梁的Q 图和M 图。
(a )(b )8 8R DQ 图(kN)(c )图9-18 例9-18图【例9-7】 一外伸梁，梁上荷载如图9-18a 所示，已知l ＝４m ，利用微分关系绘出外伸梁的剪力图和弯矩图。
