黄昆 固体物理 课件(全)
- 格式:pdf
- 大小:7.19 MB
- 文档页数:274
̯ ҂➘⤵⮳ⵃ⾥ 䆐
҂➘⤵ ⵃ⾥ ҂⮳㐂 ㏳ ㇁ 喈 Ƞ⻪ Ƞ⩤ ͺ䬣Ⱗρҋ⩗̽䓿 㻳 Д䬿 㘬̽⩗䕃⮳ ⼀ȡ
҂ ㆪ
҂喈 喉喚 ̯ ⮳ 㻳 ⮳ ҂喈䪮⼺ 喉喌Һ 喚 ♥⮳ ⯿ȠⅣ Д ϩ ⮳ ҂䩆Ƞ 䘬 ҂喛
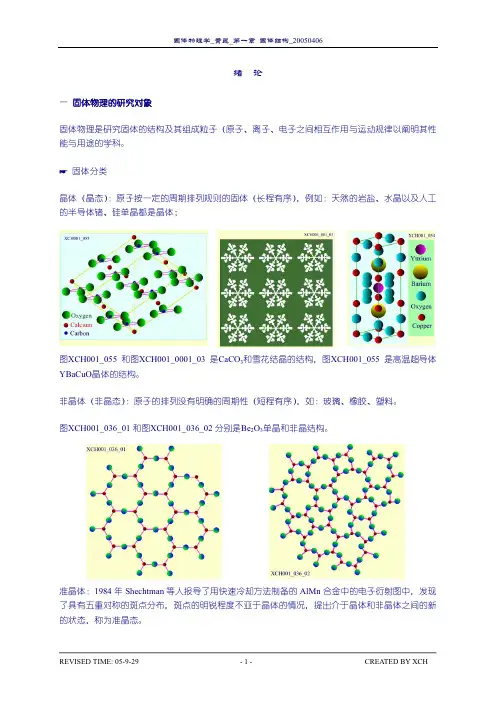
XCH001_055 XCH001_0001_03 CaCO3 䰙㟠㐂 ⮳㐂 喌 XCH001_055 倇⍘䊴 ҂YBaCuO ҂⮳㐂 ȡ
䲍 ҂喈䲍 喉喚 ⮳ ⇐ ⮳ 喈ⴜ⼺ 喉喌 喚⣪⦲Ƞᾐ㘥Ƞ ȡ
XCH001_036_01 XCH001_036_02 Be2O3 䲍 㐂 ȡ
҂喚1984 Shechtmanへϩ ε⩗ 䕎 ∄ ⮳AlMn 䜀͜⮳⩤ 㵼 ͜喌 ⣟ε σ䛼 ⼟⮳ ◨ 喌 ◨⮳ 䨿⼺ ̼ων ҂⮳ 喌 Ϻν ҂ 䲍 ҂ͺ䬣⮳ ⮳⟥ 喌⼟ͩ ȡ
⤵ ҂喚 㐂 㻳 ⮳ ҂喌 ҂喛
䭴 ҂喚 ҂͜ ̼㻳 喌 㻳 喈 喉⮳㗻 ͜ 䛾̼㻳 ⮳ ҂ 䔀ͽ ⮳ ҂ȡ
λ ҂➘⤵⮳ 䓶⼺
҂ 㻳 ⮳ ҄ ⟥ ҂ ⮳ ⼟ ̽ Ѕ➘⤵ 䉗ͺ䬣 ̯ 㖃㈪喛 ҂ ⮳㻳 䘗㻳 ⮳ ȡ
̲ͅ㏙ 喈䄄 ДṜ⤲ ⼞⮳ὐ 㼒䛹 㼒ⴢ⮳ 䉗 㼒⤵䲑喛
ͅ㏙喌䭮㓬ӌ䃓ͩ 㼒ⴢ ҂ ⩠̯ϊ ⮳ȠⰧ ⮳Ƞ 㵻 䲑 ⮳ Ć ⴢć 㻳 䛼 䯵㔻 ⮳ 䔈͙ ⵯ̹喛
Όͅ㏙͜ 喌 㤡 ε⾩䬣◨䭤 䄣喌ằ ε ⮳➨ ȡ
Όͅ㏙ 喛䉨 ≊ 喌⚹ Ƞ 㒆へ⠛⿺ ε ν ҂ 㻱 ҄㐂 ⮳⤵䃩҂㈪喌ͩ䔊̯ₔⵃ⾥ ҂㐂 ⮳㻳 ӊε⤵䃩ӌ 喌 ⼞㉞⮳ 䛾 侻κ Όͅ㏙ϩЛ䔇 㐂ε㠔 䛼㺰⮳㏾侻㻳 Һ ν ҂℃☜⮳ 䮵⣯ 喌 ν䜀 ☜ ⩤ 䉗⮳偾 喍Ҋ 喌ͩε䔊̯ₔε㼒䔈ϊ㏾侻㻳 ⮳ 䉗喌 ⣟ε̯ϊ 䄣ȡ
ͅ㏙ ➨冰 ≊ѕ ⿺ε㏾ ⮳䜀 㜙⩠⩤ 䃩へ喌 ͅ㏙ 喌䔀В➘⤵ ⮳ 喌ҮϩЛ ҂⮳䃓䃵䔊 ε̯͙ ⮳䭥⃤Ƞ 喌X ㏮ ӊεϩㆪⰣ ⿔ ҂ 䘗㐂 ⮳ ȡ






第一章晶体结构§1-1 绪论固体物理与力学、电动力学、量子力学等学科不同,这些学科学习的是一种运动形式,而固体物理学习的则是一类物质,固体物理学习晶体的几何结构,学习形成晶体结构的原子的最普遍的运动形式,即晶格振动,学习晶体中的能量特征和运动,然后学习半导体物理超导电性等一些专题问题。
引入:固体是指在承受切应力时具有一定程度刚性的物质。
在相当长的时间里,人们研究的固体主要是晶体,晶体知识作为一门科学的出现,科学界公认是在17世纪中叶,距今已有300多年。
固体是由什么原子组成?它们是怎样排列和结合的?这种结构是如何形成的?一、固体物理的研究对象固体物理是研究固体的微观结构,组成固体的粒子(原子、离子、电子)之间相互作用与运动规律,并在此基础之上阐明固体的宏观性质和应用的学科。
它分为:晶体、非晶体和准晶体三类。
1、晶体:原子按一定的周期排列成规则的固体(即,长程有序) 例如:天然的岩盐、水晶以及人工的半导体锗、硅单晶都是晶体。
——图XCH001_055 和图XCH001_0001_03 是CaCO3和雪花结晶的结构——图XCH001_055 是高温超导体YBaCuO晶体的结构2、非晶体:原子的排列没有明确的周期性(短程有序),如:玻璃、橡胶、塑料。
——图XCH001_036_01 和图XCH001_036_02 分别是Be2O3单晶和非晶结构。
3、准晶体:介于晶体和非晶体之间的新的状态——称为准晶态。
理想晶体:内在结构完全规则的固体,又叫做完整晶体;实际晶体:固体中或多或少地存在有不规则性,在规则(排列)的背景中尚存在微量不规则性的晶体——近乎完整的晶体。
二固体物理的研究方法固体物理主要是一门实验性学科。
为了阐明所揭示出来的现象之间内在的本质联系,需要建立和发展关于固体的微观理论。
固体(晶体)是一个很复杂的客体,每一立方米中包含10个原子、电子,而且它们之间的相互作用相当强.固体的宏观性质就是如此大量有约23的粒子之间的相互作用和集体运动的总表现。


§1.5 晶体的宏观对称性晶体在几何外形上表现出明显的对称性,同时这些对称性性质也在物理性质上得以体现。
—— 介电常数可以表示为一个二阶张量:),,,(z y x =βαεαβ—— 电位移分量∑=ββαβαεE D可以证明对于立方对称的晶体:αβαβδεε0=——对角张量所以:E D KK 0ε=—— 介电常数可以看作一个简单的标量。
在六角对称的晶体中,如果将坐标轴选取在六角轴和垂直于六角轴的平面内,介电常数具有如下形式: ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⊥⊥εεε000000//对于平行轴(六角轴)的分量://E //////E D ε=对于垂直于轴(垂直于六角轴的平面)的分量:⊥E ⊥⊥⊥=E D ε正是由于六角晶体的各向异性,而具有光的折射现象。
而立方晶体的光学性质则是各向同性的。
原子的周期性排列形成晶格,不同的晶格表现出不同的宏观对称性,怎样描述晶体的宏观对称性? 概括晶体宏观对称性的系统方法就是考察晶体在正交变换的不变性。
在三维情况下,正交变换表示为:⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛=⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛→⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛z y x a a a a a a a a a z y x z y x 331313232212131211'''—— 矩阵是正交矩阵。
3,2,1,},{=j i a ij —— 如图XCH001_062所示,绕z 轴转θ角的正交矩阵: ⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−1000cos sin 0sin cos θθθθ—— 中心反演的正交矩阵:⎟⎟⎟⎠⎞⎜⎜⎜⎝⎛−−−100010001—— 一个变换为空间转动,矩阵行列式等于+1; —— 变换为空间转动加中心反演,矩阵行列式等于-1。
一个物体在某一个正交变换下保持不变,称之为物体的一个对称操作,物体的对称操作越多,其对称性越高。
1 立方体的对称操作1) 绕三个立方轴转动:23,,2πππ,共有9个对称操作;如图XCH001_026_01所示。

