6—5 电容 电场的能量 电介质的相对电容率.
- 格式:ppt
- 大小:624.00 KB
- 文档页数:14




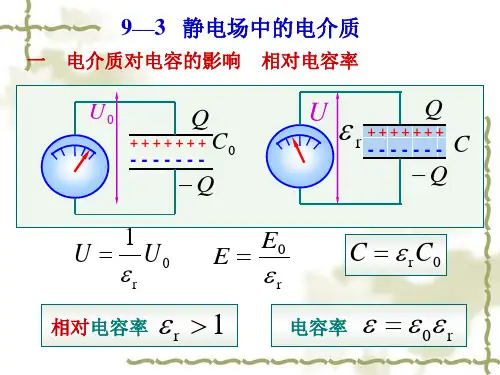
电容与电介质介电常数与电场能量与电场能量密度之间的关系电容是电学中一个重要的概念,它描述了电路元件对电荷的存储能力。
而电介质介电常数则是衡量电介质的极化能力,它与电场能量和电场能量密度之间存在紧密的关系。
首先,让我们回顾一下电容的概念。
电容是电路元件对电荷存储能力的度量,用单位电压下的电容量来表示。
在一个理想的理论电容器中,电容量的计算公式为C = Q/V,其中C表示电容量,Q表示电荷量,V表示电压。
这意味着当电容器的电压增加时,可以存储的电荷量也会增加。
然而,在实际的应用中,电容器常常由电介质填充,以增加电容量。
电介质介电常数是衡量电介质极化能力的物理量,用εr来表示。
理想情况下,如果电介质介电常数为1,则电介质对电场几乎没有影响。
但是,在实际情况下,绝大多数电介质都有介电常数大于1,这意味着它们能够存储更多的电荷。
因此,对于一个实际的电容器而言,其电容量的计算公式可以表示为C = εrε0A/d,其中ε0表示真空中的介电常数,A表示电容器的极板面积,d表示极板之间的距离。
由此可见,电介质介电常数的增加会导致电容量的增加。
现在,让我们思考一下电场能量与电场能量密度之间的关系。
在电磁学中,电场能量是电场对电荷进行的功的总和。
假设一个点电荷q在电场E中移动一个距离d,那么它所受到的力F等于qE,因此电场对电荷所做的功W等于F·d = qEd。
由此可见,电场能量与电荷量、电场强度和电位移之间存在紧密的联系。
而电场能量密度则是单位体积内的电场能量,用u表示。
它表示了电场能量在空间中的分布情况。
对于一个电容器而言,它的电场能量密度可以表示为u =1/2εE²,其中ε表示电介质介电常数,E表示电场强度。
这意味着电场能量密度的大小与电介质的极化能力和电场强度成正比。
综上所述,电容与电介质介电常数与电场能量和电场能量密度之间存在着密切的关系。
电介质的介电常数决定了电容器的电容量,而电场能量和电场能量密度则分别与电介质的极化能力和电场强度有关。

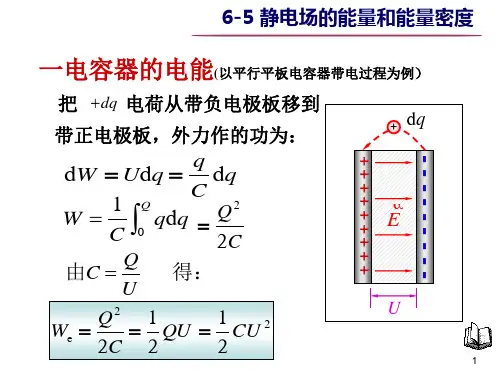
1-1、试比较电介质中各种极化的性质和特点。
在外电场的作用下,介质原子中的电子运动轨道将相对于原子核发生弹性位移,此为电子式极化或电子位移极化。
离子式结构化合物,出现外电场后,正负离子将发生方向相反的偏移,使平均偶极距不再为零,此为离子位移极化。
极性化合物的每个极性分子都是一个偶极子,在电场作用下,原先排列杂乱的偶极子将沿电场方向转动,显示出极性,这称为偶极子极化。
在电场作用下,带电质点在电介质中移动时,可能被晶格缺陷捕获或在两层介质的界面上堆积,造成电荷在介质空间中新的分布,从而产生电矩,这就是空间电荷极化。
补充:1、说明巴申定律的实验曲线的物理意义是什么?答:巴申曲线如下图所示:其物理意义在于:在均匀的电场中,击穿电压b U 是气体的相对密度δ、极间距离S 乘积的函数,只要S ⋅δ的乘积不变,b U 也就不变。
其原因可解释如下:假设S 保持不变,当气体密度δ增大时,电子的平均自由行程缩短了,相邻两次碰撞之间,电子积聚到足够动能的几率减小了,故b U 必然增大。
反之当δ减小时,电子在碰撞前积聚到足够动能的几率虽然增大了,但气体很稀薄,电子在走完全程中与气体分子相撞的总次数却减到很小,欲使击穿b U 也须增大。
故在这两者之间,总有一个δ值对造成撞击游离最有利,此时b U 最小。
同样,可假设δ保持不变,S 值增大时欲得一定的场强,电压必须增大。
当S 值减到过小时,场强虽大增,但电于在走完全程中所遇到的撞击次数己减到很小,故要求外加电压增大,才能击穿。
这两者之间,也总有一个S 的值对造成撞击游离最有利,此时b U 最小。
第一章1-4、电解质电导与金属电导本质区别为何?答:金属导电的原因是自由电子移动;电介质通常不导电,是在特定情况下电离、化学分解或热离解出来的带电质点移动导致。
1-6、某些电容量较大的设备经直流高压试验后,其接地放电时间要求长达5--10min ,为什么?答:由于介质夹层极化,通常电气设备含多层介质,直流充电时由于空间电荷极化作用,电荷在介质夹层界面上堆积,初始状态时电容电荷与最终状态时不一致;接地放电时由于设备电容较大且设备的绝缘电阻也较大则放电时间常数较大(电容较大导致不同介质所带电荷量差别大,绝缘电阻大导致流过的电流小,界面上电荷的释放靠电流完成),放电速度较慢故放电时间要长达5~10min 。



目录1. 质点的运动及其规律 (5)1.1 质点运动的描述 (5)1.2 圆周运动 (5)1.4 牛顿定律 (6)1.4.1 牛顿三定律 (6)1.4.2 几种常见的力 (6)2. 动量守恒定律和能量守恒定律 (6)2.1 质点和质点系的动量定理动量守恒定律 (6)2.2 动能定理保守力与非保守力能量守恒定律 (7)3. 刚体与流体 (7)3.1 刚体的定轴转动 (7)3.1.2 刚体绕定轴转动的角速度和角加速度 (7)3.1.3 力矩转动定律转动惯量 (8)3.2 刚体定轴转动的角动量角动量定理角动量守恒定律 (8)4. 机械振动与机械波 (9)4.1 简谐运动旋转矢量简谐运动的能量 (9)4.1.1 简谐运动 (9)4.1.2 旋转矢量 (10)4.1.3 弹簧振子的能量 (10)4.2两个同向同频率简谐运动的合成 (10)4.4 机械波 (10)4.4.1 机械波的形成波长周期和波速 (10)4.4.2 平面简谐波的波函数 (11)4.5 惠更斯原理波的衍射和干涉 (11)4.5.2 波的干涉 (11)5. 气体动理论和热力学 (11)5.1 平衡态理想气体物态方程热力学第零定律 (11)5.1.1 气体的物态参量 (11)5.1.3 理想气体物态方程 (12)5.2 气体分子热运动及其统计规律 (12)5.2.2 气体分子速率分布律 (12)5.3 理想气体的压强公式平均平动动能与温度的关系 (13)5.4 能量均分定理理性气体的内能 (13)5.5 准静态过程热力学第一定律 (13)5.6 理想气体的等值过程和绝热过程 (13)5.6.1等体过程 (13)5.6.2等压过程 (14)5.6.3等温过程 (14)5.6.4绝热过程 (14)5.7 循环过程热力学第二定律 (15)5.7.2 热机和制冷机 (15)5.7.3 卡诺循环 (15)5.7.4热力学第二定律 (15)6. 静电场 (15)6.1 电场强度 (15)6.1.3 电场强度 (16)6.2 高斯定理 (17)6.2.2 电场强度通量 (17)6.2.3 高斯定理 (17)6.2.4 高斯定理应用举例 (17)6.3 静电场的环路定理电势 (18)6.3.1 静电场力所做的功 (18)6.3.2 静电场的环路定理 (18)6.3.3 电势能 (18)6.3.4 电势 (18)6.4 静电场中的导体 (19)6.4.2 静电平衡时导体上电荷的分布 (19)6.5 电容电场的能量电介质的相对电容率 (19)6.5.1 电容器及其电容 (19)7. 恒定磁场和电磁效应 (20)7.1 恒定电流电流密度电动势 (20)7.1.1 电流 (20)7.1.2 电流密度 (20)7.1.3 电源的电动势 (20)7.2 磁感强度毕奥-萨戈尔定律磁场的高斯定理 (20)7.2.1 磁感强度 (20)7.2.2 毕奥-萨戈尔定律 (21)7.4 安培环路定理 (21)8. 光学 (22)8.2 光的干涉 (22)8.2.2 杨氏双缝干涉实验 (22)8.2.3 薄膜干涉 (22)8.3光的衍射 (23)8.3.2 单缝衍射 (23)8.3.4 圆孔衍射光学仪器的分辨本领 (23)1. 质点的运动及其规律1.1 质点运动的描述位矢 r xi y j zk =++x 位矢大小 2r x y z =++质点运动方程 ()()()()r r t x t i y t j z t k ==++ 位移 B A r r r ∆=-速度 d d x y rv v v t==+平均速度 r v t∆=∆ 加速度 d d va t=1.2 圆周运动角速度 d d tθω=线速度与角速度转换v r ω=法向加速度 22n v a r rω==切向加速度 d d t v a t=1.4 牛顿定律 1.4.1 牛顿三定律牛顿第一定律 0,F v ==常矢量 牛顿第二定律 p mv = 牛顿第二定律的推论 d d()d d p mv F ma t t=== 牛顿第三定律 F F '=- 1.4.2 几种常见的力万有引力 122r m m F Ge r= 摩擦力 f N F F μ=2. 动量守恒定律和能量守恒定律2.1 质点和质点系的动量定理 动量守恒定律d d d d p F F t p t=⇒=质点的动量定理212121()d t t F t t p p mv mv =-=-⎰质点系的动量定理21ex011d n nt i i i i t i i F t m v m v ===-∑∑⎰或 0I p p =-动量守恒定律 1ni ii p m v===∑常矢量在直角坐标系中的动量守恒定律 ex 1ex2ex 3,(0),(0),(0)x i ix x y i iy y z i izz p m v C F p m v C F p m v C F ⎧===⎪⎪===⎨⎪===⎪⎩∑∑∑2.2 动能定理 保守力与非保守力能量守恒定律功 d d cos d BBAAW W F r F s θ===⎰⎰⎰质点的动能定理 2122212111d 22v k k v W mv v mv mv E E ==-=-⎰万有引力做功 11B A W Gm m r r ⎛⎫'=- ⎪⎝⎭重力做功 W mgh = 弹性力做功 22211122W kx kx ⎛⎫=-- ⎪⎝⎭势能 p W E =-∆3. 刚体与流体3.1 刚体的定轴转动3.1.2 刚体绕定轴转动的角速度和角加速度角速度 d d t θω=角加速度 d d tωα=常用的计算式子 022002002()2t t t ωωαωωαθθθθωα=+⎧⎪=+-⎨⎪=++⎩线速度与角速度转换 v r ω=切向加速度 t a r α= 法向加速度 2n a r ω= 3.1.3 力矩 转动定律 转动惯量力矩 sin M Fd Fr θ==转动定律 22iiiiM r m r m αα=∆=∆∑∑转动惯量 2iiJ r m =∆∑在质量元连续分布的刚体的转动惯量 2d J r m =⎰在质量元连续分布的刚体的转动定律 M J α= 常用的几种刚体的转动惯量:细棒(绕中轴) 212ml J = (绕一端) 23ml J =球体 225mR J = 圆筒 ()22212m J R R =+3.2 刚体定轴转动的角动量 角动量定理 角动量守恒定律角动量定理22112121d d t L t L M t L L L J J ωω==-=-⎰⎰角动量守恒定律 ex0M J ω=⇒=常量4. 机械振动与机械波4.1 简谐运动 旋转矢量 简谐运动的能量 4.1.1 简谐运动弹簧振子回复力 F kx =- 加速度 F k a x m m==- 角频率转换 2kmω=变换后的加速度 2a x ω=-周期22T ππω==频率 12v T ωπ==角频率含义 2v ωπ=简谐运动方程 cos()x A t ωϕ=+速度 d sin()d xv A t t ωωϕ==-+加速度 222d cos()d x a A t tωωϕ==-+ 振幅A =tan v x ϕω-=,后多用有旋转矢量法代替。
西南科技大学2019-2020-2学期《电介质物理》学习测验一、名词解释(每题4分,共20分)1、离子位移极化:在外电场作用下原来正负电荷中心重合的分子发生正、负电荷中心分离,形成偶极矩的现象。
2、退极化电场:由极化电荷产生的场强被称为退极化电场。
3、电介质的极化:在电场作用下,电介质内部沿电场方向出现宏观偶极子,在电介质表面出现束缚电荷(极化电荷)的现象。
4、电偶极子:两个相距很近的等量异号点电荷组成的系统。
5、极化强度P:单位体积电介质的电偶极矩矢量总和。
6、电介质的损耗:在电场作用下,电介质将部分电能转变成热能的物理过程。
7、电介质的损耗包括:电导损耗,松弛极化损耗,谐振损耗。
8、电介质的热击穿:在电场作用下,电介质内部热量积累、温度过高而导致失去绝缘能力。
9、电介质的电击穿:电场使电介质中积聚起足够数量和能量的带电质点而导致电介质失去绝缘性能。
二、填空题(每空3分,共30分):1、一平行板真空电容器,极板的自由电荷面密度为δ,现充以介电系数为εr的介质。
如果板上的自由电荷面密度δ不变,则有:真空时板间场强E=δ/ε0,电位移D= δ ,极化强度P= 0 ;充以介质时场强E= δ/ε0 εr,电位移D= δ ,极化强度P= δ(1-1/εr) ,极化电荷产生的场强为δ(1-εr) /ε0εr。
3、根据电介质的极化微观机理,极化可分为:电子和离子位移极化,偶极子转向极化,热离子松弛极化,空间电荷极化。
1、气体在均匀电场中自持放电的条件:正离子在阴极表面碰撞产生 二次电子 ;非自持放电到自持放电的关系式: (3分)。
2、电介质的击穿包括: 热 击穿, 电 击穿, 电化学 击穿。
三、简述及问答题(共20分)1、已知洛伦兹有效场E e =E (εr +2)/ 3,试推导克劳休斯—莫索缔方程。
解:1、流经实际介质电容器的电流由哪几部分组成?作图说明。
解:电导电流,位移极化电流,松弛极化电流(有功,无功)。
习题解析6-1在坐标原点及0)点分别放置电量61 2.010Q C -=-⨯及62 1.010Q C -=⨯的点电荷,求1)P -点处的场强。
解 如图6.4所示,点电荷1Q 和2Q 在P 产生的场强分别为 1122122201102211,44Q r Q r E E r r r r πεπε== 而12123,,2,1r i j r j r r =-=-==,所以()()11111222011011662203111441 2.010 1.010422113.9 6.810Q r Q r E E E r r r r j j i j N C πεπεπε--=+=+⎛⎫-⨯-⨯-=+ ⎪ ⎪⎝⎭≈-+⨯∙总 6-2 长为15l cm =的直导线AB 上,设想均匀地分布着线密度为915.0010C m λ--=⨯⋅,的正电荷,如图6.5所示,求:(1)在导线的延长线上与B 端相距1 5.0d cm =处的P 点的场强;(2)在导线的垂直平分线上与导线中点相距2 5.0d cm =处的Q 点的场强。
解 (1)如图6.5(a )所示,以AB 中点为坐标原点,从A 到B 的方向为x 轴的正方向。
在导线AB 上坐标为x处,取一线元dx ,其上电荷为 dq dx λ= 它在P 点产生的场强大小为 2200111442dq dxdE r l d x λπεπε==⎛⎫+- ⎪⎝⎭方向沿x 轴正方向。
导线AB 上所有线元在P 点产生的电场的方向相同,因此P 点的场强大小为()1212122000112112992122111114442115.0010910 6.75105102010dq dx E r d l d l d x V m λπεπεπε------⎛⎫===- ⎪-⎛⎫⎝⎭+- ⎪⎝⎭⎛⎫=⨯⨯⨯⨯-=⨯∙ ⎪⨯⨯⎝⎭⎰方向沿x 轴正方向。
(2)如图6.5(b )所示,以AB 中点为坐标原点,从A 到B 的方向为x 轴正方向,垂直于AB 的轴为y 轴,在导线AB 上坐标为x 处,取一线元dx ,其上的电荷为 dq dx λ= 它在Q 点产生的电场的场强大小为 22220021144dq dx dE r d x λπεπε==+ 方向如图6.5(b )所示。