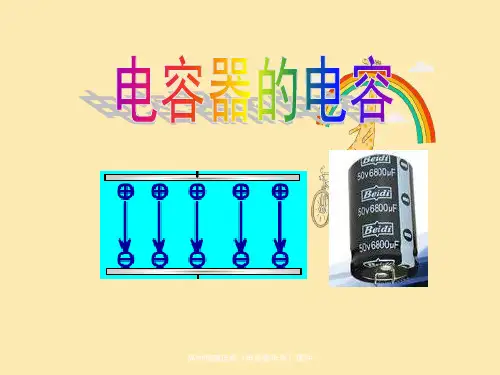
平板电容器中电场是均匀的,单位体积的电场能量是:
可以证明,上式虽然从特例导出,但这是一个普遍适用公式,对任意电场都是正确的,因此,计算任一带电系统整个电场的能量为:
电场空间所存储的能量
解:
例1 如图所示,球形电容器的内、外半径分别为R1和R2,所带电荷为±Q.若在两球壳间充以电容率为 的电介质,问此电容器贮存的电场能量为多少?
+
+
+
Q
-Q
-
讨论:改变电容器的电容的方法 S d
2) 同轴柱形电容器的电容
RA
RB
L
设长为L, 带电量为q , 内半径为 , 外半径为
3) 同心球形电容器的电容
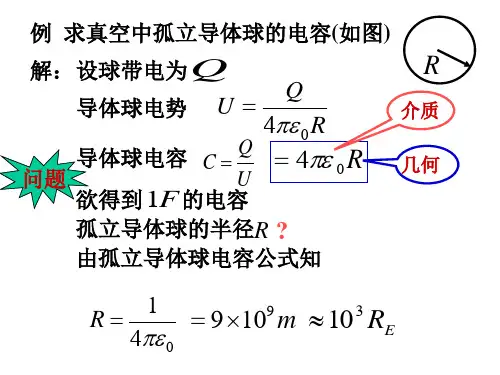
孤立导体球电容
+
+q
+
单击此处输入你的正文
+
设内球面半径RA,外球面半径RB,带电量为q + + + +
(2)介质外任一点P电势
球为等势体,电势为,
介质内任一点Q电势
R
PART 01
例4 常用的圆柱形电容器,是由半径为R1的长直圆柱导体和同轴的半径为R2的薄导体圆筒组成,并在直导体与导体圆筒之间充以相对电容率为 的电介质.设直导体和圆筒单位长度上的电荷分别为 和 .求(1)电介质中的电场强度、电位移和极化强度;(2)电介质内、外表面的极化电荷面密度; (3)此圆柱形电容器的电容.
+ + + + + + + + +
- - - - - - - - -
+
当电容器极板带电 ,两板电势差为 时,把电荷元 从B板移到A板,外力克服电场力作功为: