计算理论课后习题答案

大学计算机基础课后题答案第1章计算机基础知识一、选择题1.B2.B3.B4.B5.B6.B7.C8.D 9.B 10.D 11.C 12.A 13.B 14.D二、填空题1、1946 美国ENIAC2、4 电子管晶体管集成电路超大规模集成电路3、超导计算机量子计算机光子计算机生物计算机神经计算机4、专用计算机通用计算机5、信息基础技术信息系统技术信息应用技术6、运算器控制器存储器输入设备输出设备7、7445 682 3755 30088、0292 1717 A2FC B1B1 B7D9 E4AE9、500010、72 128三、问答题1、运算速度快计算精度高具有记忆和逻辑判断能力具有自动运行能力可靠性高2、巨型机大型机小型机微型机服务器工作站3、数据计算信息处理实时控制计算机辅助设计人工智能办公自动化通信与网络电子商务家庭生活娱乐4、计算机的工作过程就是执行程序的过程，而执行程序又归结为逐条执行指令：（1）取出指令：从存储器中取出要执行的指令送到CPU内部的指令寄存器暂存；（2）分析指令：把保存在指令寄存器中的指令送到指令译码器，译出该指令对应的操作；（3）执行指令：根据指令译码器向各个部件发出相应控制信号，完成指令规定的操作；（4）一条指令执行完成后，程序计数器加1或将转移地址码送入程序计数器，然后回到（1）。

为执行下一条指令做好准备，即形成下一条指令地址。

5、计算机自身电器的特性，电子元件一般有两个稳定状态，且二进制规则简单，运算方便。

四、操作题1、（111011）2=（59）10=（73）8=（3B）16（11001011）2=（203）10=（313）8=（CB）16（11010.1101）2=（26.8125）10=（32.64）16=（1A.D）162、（176）8=（1111110）2（51.32）8=（101001.011010）2（0.23）8=（0.010011）23、（85E）16=（100001011110）2（387.15）16=（001110000111.00010101）24、（79）=（01001111）原码=（01001111）反码=（01001111）补码（-43）=（10101011）原码=（11010100）反码=（11010101）补码第2章计算机硬件及软件系统一、选择题1.A2.D3.D4.C5.B6.C7.C8.A9.D 10.B 11.D 12.C 13.C 14.B 15.D 16.A 17.C 18.D 19.D 20.D二、填空题1、系统应用2、运算控制单元存储器输出/输入设备3、数据库管理系统4、1000赫兹5、ROM RAM Cache6.、RAM 数据丢失7、U盘的文件管理系统中密码8、同一部件内部连接同一台计算机各个部件主机与外设9、数据总线地址总线控制总线10、32 6411、图形加速接口12、CPU与内存内存13、控制器运算器14、CPU与内存15、指令数据16、CPU与内存及显存间数据的交换第3章操作系统基础一、选择题1.C2.B3.A4.D5.A6.D7.B8.B 9.B 10.A 11.B 12.B 13.A 14.B二、填充题1、文件管理2、并发性3、EXIT4、Am*.wav5、开始6、Alt+PrintScreen7、PrintScreen8、Ctrl+Z9、全选10、添加/删除程序11、输入法三、问答题1、管理和协调计算机各部件之间的资源分配与运行，它是计算机所有硬件的大管家，是用户与计算机的接口。

W5.1 证明EQ CFG 是不可判定的。

解：只须证明ALL CFG ≤m EQ CFG 即可。

构造CFG G 1，使L(G 1)=∑*。

设计从ALL CFG 到EQ CFG 的归约函数如下： F=“对于输入＜G ＞，其中G 是CFG ：1）输出＜G,G 1＞。

”若＜G ＞∈ALL CFG ，则<G,G 1>A ∈EQ CFG 。

若＜G ＞∉ALL CFG ，则<G, G 1>∉EQ CFG 。

F 将ALL CFG 归约到EQ CFG 即ALL CFG ≤m EQ CFG∵ALL CFG 是不可判定的，∴EQ CFG 是不可判定的。

5.2证明EQ CFG 是补图灵可识别的。

证明：注意到A CFG ={<G,w>|G 是能派生串w 的CFG}是可判定的。

构造如下TM ： F=“输入<G,H>，其中G,H 是CFG ，1) 对于字符串S 1, S 2,⋯，重复如下步骤。

2) 检测S i 是否可以由G 和H 派生。

3) 若G 和H 中有一个能派生w ，而另一个不能，则接受。

”F 识别EQ CFG 的补。

5.3 略。

5.4 如果A ≤m B 且B 是正则语言，这是否蕴涵着A 也是正则语言？为什么？ 解：否。

例如：对非正则语言A={0n 1n |n ≥0}和正则语言B={0}，可以构造一个可计算函数f 使得：f(w)=⎩⎨⎧≠=n n nn 10w 1,10w 0, 于是w ∈A ⇔f(w)∈B,故A ≤m B 。

5.5 证明A TM 不可映射规约到E TM 。

证明：反证法假设A TM ≤m E TM ， 则有TM m TM E A ≤。

而A TM 的补不是图灵可识别的，从而可知E TM 的补也不是图灵可识别的。

下面构造一个识别E TM 的补的图灵机S ：S=“输入<M>，M 是TM,1) 对i=1,2,…重复下一步。

2) 对S 1,S 2,…,S i 模拟M 运行i 步，若有接受，则接受。

计算机导论课后习题答案(总21页) -本页仅作为预览文档封面，使用时请删除本页-计算机导论课后习题答案汇编第一章一、简答题1、什么是计算机计算机系统是一种能够按照事先存储的程序，自动、高速的对数据进行输入、处理、输出和存储的系统。

一个计算机系统包括硬件和软件两大部分。

2、解释冯·诺依曼所提出的“存储程序”概念。

把程序和数据都以二进制的形式同意存放在存储器中，由机器自动执行。

不同的程序解决不同的问题，实现了计算机通用计算的功能，3、计算机有哪些主要的特点运算速度快`精度高计算机的字长越长，其精度越高，现在世界上最快的计算机每秒可以运算几十万次以上。

一般计算机可以有市纪委甚至几十位（二进制）有效数字，计算精度可由千分之几到百万分之几，是任何计算工具所望尘莫及的。

具有逻辑判断和记忆能力计算机有准确的逻辑判断能力和高超的记忆能力。

能够进行各种逻辑判断，并根据判断的结果自动决定下一步应该执行的指令。

高度的自动化和灵活性计算机采取存储程序方式工作，即把编号的程序输入计算机，机器便可依次逐条执行，这就使计算机实现了高度的自动化和灵活性。

4、计算机有哪些主要的用途（1）科学计算（2）数据处理(3) 实时控制（4）人工智能（5）计算机辅助工程和辅助教育（6）娱乐和游戏5、计算机发展中各个阶段的主要特点是什么第一代计算机特征是采用电子管作为主要元器件第二代计算机特征是采用晶体管作为主要器件第三代计算机特征是半导体中小规模集成电路第四代计算机特征是大规模和超大规模集成电路6信息化社会的主要特点是什么1·建立完善的信息基础设施2·采用现金的信息技术3·建立广泛的信息产业4·拥有高素质的信息人才5·构建良好的信息环境7、信息化社会对计算机人才的素质和知识结构有哪些要求在信息化社会中所需要的计算机人才是多方位的，不仅需要研究型、设计型的人才，而且需要应用型的人才；不仅需要开发型人才而且需要维护型、服务型、操作型的人才。

现代科学工程计算基础课后答案《现代科学与工程计算基础》较为详细地介绍了科学与工程计算中常用的数值计算方法、基本概念及有关的理论和应用。

全书共分八章，主要内容有误差分析，函数的插值与逼近，数值积分与数值微分，线性代数方程组的直接解法与迭代解法，非线性方程及非线性方程组的数值解法，矩阵特征值和特征向量的数值解法，以及常微分方程初、边值问题的数值解法等。

使用对象为高等院校工科类研究生及理工科类非“信息与计算科学”专业本科生，也可供从事科学与工程计算的科技工作者参考。

《现代科学与工程计算基础》讲授由浅人深，通俗易懂，具备高等数学、线性代数知识者均可学习。

基本信息出版社: 四川大学出版社; 第1版 (2003年9月1日)平装: 378页语种：简体中文开本: 32ISBN: 7561426879条形码: 9787561426876商品尺寸: 20 x 13.8 x 1.6 cm商品重量: 399 g品牌: 四川大学出版社ASIN: B004XLDT8C《研究生系列教材:现代科学与工程计算基础》是我们在长期从事数值分析教学和研究工作的基础上，根据多年的教学经验和实际计算经验编写而成。

其目的是使大学生和研究生了解数值计算的重要性及其基本内容，熟悉基本算法并能在计算机上实现，掌握如何构造、评估、选取、甚至改进算法的数学理论依据，培养和提高读者独立解决数值计算问题的能力。

目录第一章绪论§1 研究对象§2 误差的来源及其基本概念2.1 误差的来源2.2 误差的基本概念2.3 和、差、积、商的误差§3 数值计算中几点注意事项习题第二章函数的插值与逼近§1 引言1.1 多项式插值1.2 最佳逼近1.3 曲线拟合§2 Lagrange插值2.1 线性插值与抛物插值2.2 n次Lagrange插值多项式2.3 插值余项§3 迭代插值§4 Newton插值4.1 Newton均差插值公式4.2 Newton差分插值公式§5 Hermite插值§6 分段多项式插值6.1 分段线性插值6.2 分段三次Hermite插值§7 样条插值7.1 三次样条插值函数的定义7.2 插值函数的构造7.3 三次样条插值的算法7.4 三次样条插值的收敛性§8 最小二乘曲线拟合8.1 问题的引入及最小二乘原理8.2 一般情形的最小二乘曲线拟合8.3 用关于点集的正交函数系作最小二乘拟合8.4 多变量的最小二乘拟合§9 连续函数的量佳平方逼近9.1 利用多项式作平方逼近9.2 利用正交函数组作平方逼近§10 富利叶变换及快速富利叶变换10.1 最佳平方三角逼近与离散富利叶变换10.2 快速富利叶变换习题第三章数值积分与数值微分§1 数值积分的基本概念1.1 数值求积的基本思想1.2 代数精度的概念1.3 插值型求积公式§2 等距节点求积公式2.1 Newton—CoteS公式2.2 复化求积法及其收敛性2.3 求积步长的自适应选取§3 Romberg 求积法3.1 Romberg求积公式3.2 Richardson外推加速技术§4 Gauss型求积公式4.1 Gauss型求积公式的一般理论4.2几种常见的Gauss型求积公式§5 奇异积分和振荡函数积分的计算5.1 奇异积分的计算5.2 振荡函数积分的计算§6 多重积分的计算6.1 基本思想6.2 复化求积公式6.3 Gauss型求积公式§7 数值微分7.1 Taylor级数展开法7.2 插值型求导公式习题第四章解线性代数方程组的直接法§1 Gauss消去法§2 主元素消去法2.1 全主元素消去法2.2 列主元素消去法§3 矩阵三角分解法3.1 Doolittle分解法（或LU分解）3.2 列主元素三角分解法3.3 平方根法3.4 三对角方程组的追赶法§4 向量范数、矩阵范数及条件数4.1 向量和矩阵的范数4.2 矩阵条件数及方程组性态习题第五章解线性代数方程组的迭代法§1 Jacobi迭代法§2 Gauss-Seidel迭代法§3 超松弛迭代法§4 共轭梯度法习题第六章非线性方程求根§1 逐步搜索法及二分法1.1 逐步搜索法1.2 二分法§2 迭代法2.1 迭代法的算法2.2 迭代法的基本理论2.3 局部收敛性及收敛阶§3 迭代收敛的加速3.1 松弛法3.2 Aitken方法§4 New-ton迭代法4.1 Newton迭代法及收敛性4.2 Newton迭代法的修正4.3 重根的处理§5 弦割法与抛物线法5.1 弦割法5.2 抛物线法§6 代数方程求根6.1 多项式方程求根的Newton法6.2 劈因子法§7 解非线性方程组的Newton迭代法习题……第七章矩阵特征值和特征向量的计算第八章常微方分程数值解法附录参考文献欢迎下载，资料仅供参考!!!资料仅供参考!!!资料仅供参考!!!。

现代数值计算课后答案【篇一：数值计算课后答案4】>1、设x0?0,x1?1，写出f(x)?e?x的一次插值多项式l1(x)，并估计插值误差。

设插值函数为l1(x)?ax?b，由插值条件，建立线性方程组为?a?0?b?1??1?a?1?b?e?a?e?1?1解之得??b?1则l1(x)?(e?1?1)x?1因为y?(x)??e?x,y??(x)?e?x 所以，插值余项为r(x)?f(x)?p(x)??1f(n?1)(?)?(x)(n?1)!1(2)f(?)?(x)2!1?f(2)(?)(x?x0)(x?x1)2!1?e??(x?0)(x?1)(??(0,1))2所以1r(x)?maxe??maxx(x?1)0?x?120???1。

111??e?0??2482选用合适的三次插值多项式来近似计算f(0.2)和f(0.8)。

解：设三次插值多项式为f(x)?a0?a1x?a2x2?a3x3，由插值条件，建立方程组为?a0?a1?(?0.1)?a2?(?0.1)2?a3?(?0.1)3?0.995?23?a0?a1?0.3?a2?0.3?a3?0.3?0.995?23?a0?a1?0.7?a2?0.7?a3?0.7?0.765?a?a?1.1?a?1.12?a?1.13?0.4 5423?01即?a0?0.1a1?0.01a2?0.001a3?0.995?a0?0.1a1?0.01a2?0.001a3?0 .995?a?0.3a?0.09a?0.027a?0.995?0.4a1?0.08a2?0.028a3?0?0?1 23???a?0.7a?0.49a?0.343a?0.7650.8a1?0.48a2?0.344a3?1.76123?0?? ?0.4a1?0.72a2?0.988a3??0.311?a0?1.1a1?1.21a2?1.331a3?0.45 4??a0?0.1a1?0.01a2?0.001a3?0.995?0.4a1?0.08a2?0.028a3?0???0.32a2?0.288a3?1.76???0.384a3??3.831?解之得 ?a0?0.41?a??6.29?1?a??3.48?2??a3?9.98则所求的三次多项式为f(x)?0.41?6.29x?3.48x2?9.98x3。

李凡长版组合数学课后习题答案习题5第五章Pólya计数理论1. 计算,并指出它的共轭类. 解：题中出现了5个不同的元素：分别是：1，2，3，4，5。

即|Sn|＝5。

(123)(234)(5)(14)(23)?12345??12345??12 345? ???23145????13425????43215? ????????12345??12345????34125????432 15?? ?????12345????21435?? ???(12)(34)( 5) 的置换的型为1122而Sn中属于1122型的元素个数为个其共轭类为，，，，，，，，，，，，， 2. 设D是n元集合,G是D上的置换群.对于D 的子集A和B,如果存在??G,使得B?{?(a)|a?A},则称A与B是等价的.求G 的等价类的个数. 1n?c1(ai)，其中c1(ai)表示在置换ai作用下保持不变解：根据Burnside引理l?Gi?15!?152!1!1122的元素个数，则有c1(σI)=n; 设在σ的作用下，A的元素在B中的个数为i，则c2(σ)=n－2i；1若没有其他置换，则G诱出来的等价类个数为l=[n?(n?2i)]?n?i 23. 0,1,6,8,9组成的n位数,如果把一个数调转过来读得到另一个数,则称这两个数是相等的.例如,0168和8910,0890与0680是相等的.问不相等的n位数有多少个？解：该题可理解为相当于n位数，0，1，6，8，9这5个数存在一定的置换关系31 对于置换群G={g1,g2} g1为不动点置换，型为1n；为5n；n??n?g2置换：(2(n-1))(3(n-2))…(??2??2?) ????分为2种情况：n为奇数时12 ，但是只有中间的数字是0，1，8的时候，才可能调转过来的时候是相同的，所以这里的剩下的中间数字只能是有3种。

即：个数为3×5n2n2n?12 n2 n为偶数时 2 ，个数为 5 该置换群的轮换指标为1n122(5?5)?5 n为偶数时，等价类的个数l=221nn为奇数时，等价类的个数l=(5?3?52n?12n3n) 4. 现有8个人计划去访问3个城市,其中有3个人是一家,另外有2个人是一家.如果一家人必须去同一个城市,问有多少种方案？写出它们的模式. 解：令D={d1,d2,…,d8}，其中，d1,d2,d3为一家，d4,d5为一家。

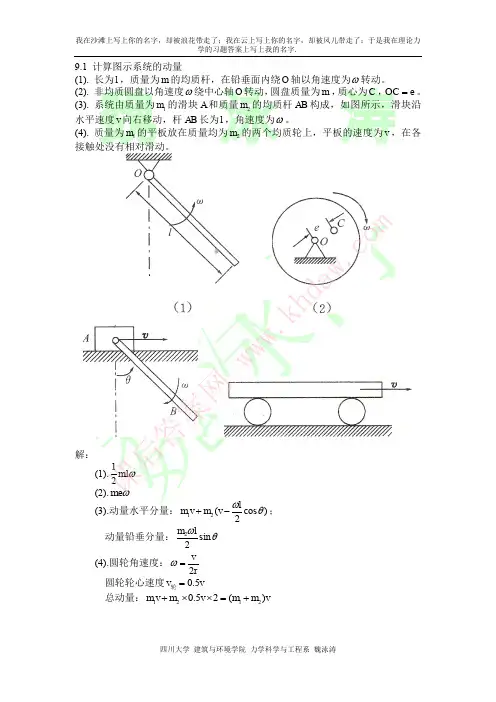
(a)A(a)O第10章 动能定理及其应用10－1 计算图示各系统的动能：1．质量为m ，半径为r 的均质圆盘在其自身平面内作平面运动。

在图示位置时，若已知圆盘上A 、B 两点的速度方向如图示，B 点的速度为v B ，θ = 45º（图a ）。

2．图示质量为m 1的均质杆OA ，一端铰接在质量为m 2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动，圆心速度为v（图b ）。

3．质量为m 的均质细圆环半径为R ，其上固结一个质量也为m 的质点A 。

细圆环在水平面上作纯滚动，图示瞬时角速度为ω（图c ）。

解：1．222222163)2(2121)2(212121BB BC C C mv r v mr v m J mv T =⋅+=+=ω 2．222122222214321)(21212121v m v m r v r m v m v m T +=⋅++=3．22222222)2(212121ωωωωmR R m mR mR T =++=10－2 图示滑块A 重力为1W ，可在滑道内滑动，与滑块A 用铰链连接的是重力为2W 、长为l 的匀质杆AB 。

现已知道滑块沿滑道的速度为1v ，杆AB 的角速度为1ω。

当杆与铅垂线的夹角为ϕ时，试求系统的动能。

解：图（a ）B A T T T +=)2121(21222211ωC C J v g W v g W ++=21221121212211122]cos 22)2[(22ωϕωω⋅⋅+⋅++++=l gW l l v l v l g W v g W]cos 31)[(2111221222121ϕωωv l W l W v W W g +++=10－3 重力为P F 、半径为r 的齿轮II 与半径为r R 3=的固定内齿轮I 相啮合。

齿轮II 通过匀质的曲柄OC 带动而运动。

曲柄的重力为Q F ，角速度为ω，齿轮可视为匀质圆盘。

试求行星齿轮机构的动能。

数值计算方法课后习题答案吕同富【篇一：《数值计算方法》(二)课程教学大纲】txt>课程编号： l124008课程类别：专业必修学分数： 3 学时数：48 适用专业：信息与计算科学应修(先修)课程：数学分析、高等代数一、本课程的地位和作用数值分析(二)为数值分析课程的第二部分，它是信息与计算科学专业的一门专业必修课。

主要内容包括函数最佳逼近、数值积分、数值微分、常微分方程数值解法。

通过本课程的学习，学生将初步具备用计算机去有效地解决实际问题的能力。

二、本课程的教学目标通过本课程的学习，使学生了解和掌握求解函数最佳逼近、数值积分、数值微分、常微分方程等问题所涉及的各种常用的数值计算方法、数值方法的构造原理及适用范围。

本课程坚持理论与实践教学并重的原则，理论上主要讲述求解函数最佳逼近、数值积分、数值微分、常微分方程等问题的基本理论和基本方法。

与此同时，通过上机实验加深学生对各种计算方法的理解，为今后用计算机去有效地解决实际问题打下基础。

三、课程内容和基本要求(“*”记号标记难点内容，“▽”记号标记重点内容，“▽*”记号标记既是重点又是难点的内容)第六章函数最佳逼近 1．教学基本要求（1）理解：几类常用的正交多项式。

（2）掌握：最佳一致逼近和最佳平方逼近。

（3）掌握：曲线拟合的最小二乘法。

2．教学内容（1）*正交多项式。

（2）▽*最佳一致逼近。

（3）▽最佳平方逼近。

（4）正交多项式的逼近性质。

（5）▽曲线拟合的最小二乘法。

第七章数值积分 1．教学基本要求（1）理解：机械求积公式的基本思想、插值型求积公式的特点。

（2）掌握：newton-cotes求积公式、复合求积公式。

（3）掌握：romberg求积公式、gauss求积公式。

2．教学内容（1）*机械求积公式。

（2）▽newton-cotes求积公式。

（3）▽复合求积公式。

（4）变步长求积公式。

（5）▽romberg求积公式。

（6）▽*gauss求积公式第八章数值微分 1．教学基本要求（1）了解：数值微分的中点法。

《大学计算机》课后习题习题一参考答案二、判断题1．电子计算机具有记忆和逻辑判断能力、计算速度快、运算精度高，但是运行过程不能自动连续进行，需人工干预。

（F）2．计算思维是计算机学科所关心的课题，与其他学科没有关系。

（F）3．人们在学习和应用计算机过程中改变了工作方式，但是，思维方式却没有变化。

（F）4．计算机是一种先进的工具，只要学会使用计算机，就能满足以后的工作要求，没有必要培养计算思维能力。

（F）5．计算思维能力培养的核心是发现问题能力、寻求解决问题的思路、分析比较不同方案和验证方案等。

（T）6．新型的光子计算机、生物计算机、量子计算机、纳米计算机是人类的设想，不可能生成制造出来。

（F）7．在计算机行业及其领域所形成的社会意识形态和伦理关系下,调整人与人之间、人与知识产权之间、人与计算机之间以及人与社会之间的行为规范总和称为计算机职业道德。

（T）8．计算机网络比任何一种媒介更能简便、有效地获取、传播、利用信息。

（T）9．计算机病毒是指编制的或者在计算机程序中插入的破坏计算机功能或者毁坏数据、影响计算机使用，并能自我复制的一组计算机指令或者程序代码。

（T）1．计算机运行速度降低一定是感染了病毒。

（F）三、选择题1．计算机发展过程按使用的电子器件不同可划分为四代，其中第二代计算机使用的器件为（B）。

A. 电子管B. 晶体管C. 中、小规模集成电路D. 大规模和超大规模集成电路3．计算机正朝两极方向发展，即（B）。

A. 专用机和通用机B. 微型机和巨型机C. 模拟计算机和数字计算机D. 单核计算机和多核计算机4．我国自行研制的第一台亿次巨型计算机是（C）。

A. 曙光B. 龙芯C. 银河ⅠD. 银河Ⅱ5．6．计算机应用最广泛的领域是（B）。

A.科学计算B. 信息处理C. 过程控制D. 人工智能7．CAI的中文含义是（D）。

A. 计算机辅助设计B. 计算机辅助制造C. 计算机辅助工程D. 计算机辅助教学8．目前大多数计算机工作原理基本上采用的是（C）。

第三章上下文无关语言略。

a. 利用语言A={a m b n c n | m,n0}和A={a n b n c m | m,n0}以及例，证明上下文无关语言在交的运算下不封闭。

b. 利用(a)和DeMorgan律(定理，证明上下文无关语言在补运算下不封闭。

证明：a.先说明A,B均为上下文无关文法，对A构造CFG C1S aS|T|T bTc|对B,构造CFG C2S Sc|R|R aRb由此知 A,B均为上下文无关语言。

但是由例, A∩B={a n b n c n|n0}不是上下文无关语言，所以上下文无关语言在交的运算下不封闭。

b.用反证法。

假设CFL在补运算下封闭，则对于(a)中上下文无关语言A,B，A,B也为CFL，且CFL对并运算封闭，所以BA 也为CFL，进而知道B A ⋃为CFL ，由DeMorgan 定律B A ⋃＝A ∩B ，由此A ∩B 是CFL,这与(a)的结论矛盾，所以CFL 对补运算不封闭。

略。

和 给出产生下述语言的上下文无关文法和PDA ，其中字母表={0,1}。

a. {w | w 至少含有3个1}S →A1A1A1A A →0A|1A|b. {w | w 以相同的符号开始和结束}S →0A0|1A1 A →0A|1A|c. {w | w 的长度为奇数,11,1 0,,1,11,1 1, 0,0,0 1,10,0 1, 0, 1,0,S →0A|1A A →0B|1B| B →0A|1Ad. {w | w 的长度为奇数且正中间的符号为0}S →0S0|1S1|0S1|1S0|0e. {w | w 中1比0多}S →A1AA →0A1|1A0|1A|AA|f. {w | w=w R}S →0S0|1S1|1|01,0 0,0,0 1,00,0 ,$ ,$1,1,10,0 ,1,$,$1,0 0,1g. 空集S →S给出产生下述语言的上下文无关文法：a ．字母表{a,b}上a 的个数是b 的个数的两倍的所有字符串组成的集合。

计算方法引论徐萃薇课后题答案徐萃薇(Xu Cuiwei)教授向学生们提出了一个有关计算方法的练习题，这里是课后习题的答案：题目一：定义“计算方法”计算方法是一种数值解决问题的方法，用计算机或者类比设备来完成一系列计算过程，以解决由某一特定问题及其变体而产生的一系列更复杂问题。

它是一种能用有限的资源（如时间、空间、技术等）产生正确结果的计算机程序，他可以安排合理的步骤，使用易于操作的方法来解决指定的问题。

题目二：分析计算方法的优缺点优点：1. 计算方法基于数理模型的明确理论，可以更好地解决问题；2. 相较于其他方法，它使用更简单的计算机程序来实现更复杂的功能；3. 它可以把不容易解决的问题转变为容易解决的形式，这将有助于系统更好地管理和管理空间。

缺点：1. 计算方法有一定的局限性，不一定适用于所有的情景；2. 数学建模常常非常耗时，而且可能有很多假设和过程；3. 数学建模的结果可能有很多偏差，可能不切实际。

题目三：对于复杂问题，需要用到哪些计算方法对于复杂问题，可以用到多种方法来解决，如：1. 动态规划法(DP)：动态规划法可以用来解决最优化问题，如旅行商问题、背包问题等。

2. 概率法：概率法可以跨越归纳和演绎，在可预期结果和把握风险方面有很大的优势。

3. 机器学习：机器学习可以帮助系统自动从数据中获取规律，从而有效地解决规模复杂的问题。

4. 启发式搜索：启发式搜索可以有效地模拟人类的求解思考方法，通过把问题分解为子问题，再变换为其他问题求解的方法，可以有效解决复杂的问题。

5. 分支定界法：分支定界法是一种能获得全局最优解的解决复杂问题的方法，它被广泛应用于思维密集型最优化问题。

总而言之，复杂问题可以用多种计算方法来解决。

正确使用和选择合适的方法是关键，从而能够获得更好的结果。