2019-2020学年浙江省温州市瑞安市集云实验学校等五校九年级(上)期末数学试卷 (解析版)

2019-2020学年浙江省温州市九年级（上）期末数学试卷一、选择题（共10小题，每小题3分，共30分）：1．已知O 的半径为4cm ，点P 在O 上，则OP 的长为( )A ．1cmB ．2cmC ．4cmD ．8cm 2．已知23a b =，则a b a +的值为( ) A ．52 B ．53 C ．32 D ．233．抛物线223y x x =-+ 的对称轴为( )A ．直线1x =-B ．直线2x =-C ．直线1x =D ．直线2x =4．如图，在O 中，点M 是AB 的中点，连结MO 并延长，交O 于点N ，连结BN ，若140AOB ∠=︒，则N ∠的度数为( )A ．70︒B ．40︒C ．35︒D ．20︒5．在一个不透明的口袋里装有2个白球，3个黑球和3个红球，它们除颜色外其余都相同，现随机从袋里摸出1个球，则摸出白球的概率是( )A ．12B ．38C ．13D ．146．如图， 四边形ABCD 是O 的内接四边形， 若3D B ∠=∠，则B ∠的度数为( )A ．30︒B ．36︒C ．45︒D ．60︒7．已知点(2,)A a -，(1,)B b ，(3,)C c 是抛物线222y x x =-+上的三点，则a ，b ，c 的大小关系为( )A ．a c b >>B ．b a c >>C ．c a b >>D ．b c a >>8．如图，正六边形ABCDEF 的边长为2，现将它沿AB 方向平移1个单位，得到正六边形A B C D E F ''''''，则阴影部分A BCDE F '''的面积是( )A ．B ．CD ．2+9．如图，在Rt ABC ∆中，20A ∠=︒，6AC =，将ABC ∆绕直角顶点C 按顺时针方向旋转得到△A B C ''，当点B '第一次落在AB 边上时，点A 经过的路径长（即AA '的长）为( )A ．23πB ．43πC ．2πD ．73π 10．如图，点A 为x 轴上一点，点B 的坐标为(,)a b ，以OA ，AB 为边构造OABC ，过点O ，C ，B 的抛物线与x 轴交于点D ，连结CD ，交边AB 于点E ，若AE BE =，则点C 的横坐标为( )A ．a b -B ．2bC ．3aD ．4a 二、填空题（共8小题，每小题3分，共24分）：11．如图，直线////AB CD EF ，已知3AC =，4CE =， 3.6BD =，则DF 的长为 ．12．某工厂从一批保温杯中随机抽取1000个进行质量检测，结果有980个保温杯质量合格，那么可以估计这批保温杯的合格率约为 ．13．请写出一个开口向上，且其图象经过原点的抛物线的解析式 ．14．已知扇形的圆心角为45︒，半径为3cm ，则该扇形的面积为 2cm ．15．如图，点P 是ABC ∆的重心，过点P 作//DE AB 交BC 于点D ，交AC 于点E ，若AB 的长度为6，则DE 的长度为 ．16．一根排水管的截面如图所示，已知水面宽40AB cm =，水的最大深度为8cm ，则排水管的半径为 cm ．17．函数28(y ax ax a =-为常数，且0)a >在自变量x 的值满足23x 剟时，其对应的函数值y的最大值为3-，则a 的值为 ．18．如图是一个摩天轮，它共有8个座舱，依次标为1~8号，摩天轮中心O 的离地高度为50米，摩天轮中心到各座舱中心均相距25米，在运行过程中，当1号舱比3号舱高5米时，1号舱的离地高度为 米．三、解答题（共6小题，共46分）：19．有三张分别标有数字2，5，9的卡片，它们的背面都相同．现将它们背面朝上，从中任意抽出一张卡片，不放回，再从剩余的两张卡片里任意抽出一张．（1）请用树状图或列表法表示出所有可能的结果．（2）求两张卡片的数字之和为偶数的概率．20．如图，在所给的方格纸中，每个小正方形边长都是1，ABC ∆是格点三角形（顶点在方格顶点处）．（1）在图1画格点△111A B C ，使△111A B C 与ABC ∆相似，相似比为2:1．（2）在图2画格点△222A B C ，使△222A B C 与ABC ∆相似，面积比为2:1．21．如图，抛物线223y x x =--与x 轴交于A ，B 两点(A 在B 的左侧），顶点为C ．（1）求A ，B 两点的坐标；（2）若将该抛物线向上平移t 个单位后，它与x 轴恰好只有一个交点，求t 的值．22．如图，在ABC ∆中，AB AC =，D 是BC 边上的中点，过A ，C ，D 三点的圆交BA 的延长线于点E，连接EC．（1）求证：90∠=︒；E（2）若6BC=，求AE的长．AB=，1023．创客联盟的队员想用3D打印完成一幅边长为4米的正方形作品ABCD，设计图案如图所示（四周阴影是四个全等的矩形，用材料甲打印；中心区是正方形A B C D''''，用材料乙打印）．在打印厚度保持相同的情况下，两种材料的消耗成本如下表设矩形的较短边AH的长为x米，打印材料的总费用为y元．（1）A D''的长为米（用含x的代数式表示）；（2）求y关于x的函数解析式；（3）当中心区的边长不小于3时，预备材料的购买资金700元够用吗？请利用函数的增减性来说明理由．24．如图，在平面直角坐标系中，(3,4)A，(5,0)B，连结AO，AB．点C是线段AO上的动点（不与A，O重合），连结BC，以BC为直径作H，交x轴于点D，交AB于点E，连结CD，CE，过E作EF x⊥轴于F，交BC于G．（1）AO的长为，AB的长为（直接写出答案）（2）求证：ACE BEF∽；∆∆（3）若圆心H落在EF上，求BC的长；（4）若CEG∆是以CG为腰的等腰三角形，求点C的坐标．参考答案与试题解析一、选择题（共10小题，每小题3分，共30分）：1．已知O 的半径为4cm ，点P 在O 上，则OP 的长为( )A ．1cmB ．2cmC ．4cmD ．8cm【解答】解：点P 在O 上，4OP cm ∴=．故选：C ．2．已知23a b =，则a b a +的值为( ) A ．52 B ．53C ．32D ．23 【解答】解：23a b =， ∴23522a b a ++==， 故选：A ．3．抛物线223y x x =-+ 的对称轴为( )A ．直线1x =-B ．直线2x =-C ．直线1x =D ．直线2x =【解答】解： 2223(1)2y x x x =-+=-+，∴对称轴为1x =，故选：C ．4．如图，在O 中，点M 是AB 的中点，连结MO 并延长，交O 于点N ，连结BN ，若140AOB ∠=︒，则N ∠的度数为( )A ．70︒B ．40︒C ．35︒D ．20︒【解答】解：点M 是AB 的中点，∴AM BM =，140AOB ∠=︒，1702BOM AOB ∴∠=∠=︒， 1352N BOM ∴∠=∠=︒， 故选：C ．5．在一个不透明的口袋里装有2个白球，3个黑球和3个红球，它们除颜色外其余都相同，现随机从袋里摸出1个球，则摸出白球的概率是( )A ．12B ．38C ．13D ．14【解答】解：口袋里装有2个白球，3个黑球和3个红球，∴口袋里共有8个球，∴摸出白球的概率是2184=； 故选：D ．6．如图， 四边形ABCD 是O 的内接四边形， 若3D B ∠=∠，则B ∠的度数为( )A ．30︒B ．36︒C ．45︒D ．60︒ 【解答】解：四边形ABCD 是O 的内接四边形，180B D ∴∠+∠=︒，3D B ∠=∠，4180B ∴∠=︒，解得：45B ∠=︒，故选：C ．7．已知点(2,)A a -，(1,)B b ，(3,)C c 是抛物线222y x x =-+上的三点，则a ，b ，c 的大小关系为( )A ．a c b >>B ．b a c >>C ．c a b >>D ．b c a >>【解答】解：抛物线2222(1)1y x x x =-+=-+，∴该抛物线的对称轴是直线1x =，当1x >时，y 随x 的增大而增大，当1x <时，y 随x 的增大而减小，点(2,)A a -，(1,)B b ，(3,)C c 是抛物线222y x x =-+上的三点，1(2)3--=，110-=，312-=，a cb ∴>>，故选：A ．8．如图，正六边形ABCDEF 的边长为2，现将它沿AB 方向平移1个单位，得到正六边形A B C D E F ''''''，则阴影部分A BCDE F '''的面积是( )A ．B ．CD ．2+【解答】解：连接A E ''，BD ，过F '作F H A E '⊥''于H ，则四边形A E DB ''是矩形，正六边形ABCDEF 的边长为2，120A F E ∠'''=︒，30F A E ∴∠'''=︒，1F H ∴'=，A H '=，A E ∴''=，将它沿AB 方向平移1个单位，1A B ∴'=，∴阴影部分A BCDE F '''的面积12112A F E BCD A E DB S S S '''∆''=++=⨯⨯+⨯=矩形， 故选：B ．9．如图，在Rt ABC∆中，20A∠=︒，6AC=，将ABC∆绕直角顶点C按顺时针方向旋转得到△A B C''，当点B'第一次落在AB边上时，点A经过的路径长（即AA'的长）为( )A．23πB．43πC．2πD．73π【解答】解：90ACB∠=︒，20A∠=︒，70B∴∠=︒，将ABC∆绕直角顶点C按顺时针方向旋转得到△A B C''，BC B C∴='，70BB C B∴∠'=∠=︒，40BCB∴∠'=︒，40ACA∴∠'=︒，∴点A经过的路径长40641803ππ⨯==，故选：B．10．如图，点A为x轴上一点，点B的坐标为(,)a b，以OA，AB为边构造OABC，过点O，C，B的抛物线与x轴交于点D，连结CD，交边AB于点E，若AE BE=，则点C的横坐标为()A ．a b -B ．2bC ．3aD ．4a 【解答】解：四边形OABC 为平行四边形，//BC OA ∴，BC OA =，设(,)C t b ，则BC a t =-，//BC AD ，EBC EAD ∴∠=∠，在EBC ∆和EAD ∆中BEC AED EB EAEBC EAD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()EBC EAD ASA ∴∆≅∆，BC AD a t ∴==-，∴点A 为OD 的中点，∴抛物线的对称轴为直线x a t =-，()a t t a a t ∴--=--，13t a ∴=． 故选：C ．二、填空题（共8小题，每小题3分，共24分）：11．如图，直线////AB CD EF ，已知3AC =，4CE =， 3.6BD =，则DF 的长为 4.8 ．【解答】解：直线////AB CD EF ，∴AC BD CE DF=， 即3 3.64DF =， 解得： 4.8DF =，故答案为：4.812．某工厂从一批保温杯中随机抽取1000个进行质量检测，结果有980个保温杯质量合格，那么可以估计这批保温杯的合格率约为 98% ．【解答】解：这批保温杯的合格率9801000100%98%=÷⨯=．故答案为：98%．13．请写出一个开口向上，且其图象经过原点的抛物线的解析式 2y x x =+ ．【解答】解：设抛物线解析式为2y ax bx c =++，抛物线开中向上， 0a ∴>，故可取1a =，抛物线过原点，0c ∴=，对称没有限制，∴可取1b =，故答案为：2y x x =+．14．已知扇形的圆心角为45︒，半径为3cm ，则该扇形的面积为 8 2． 【解答】解：2224539()3603608n r s cm πππ===， 故答案为98π． 15．如图，点P 是ABC ∆的重心，过点P 作//DE AB 交BC 于点D ，交AC 于点E ，若AB 的长度为6，则DE 的长度为 4 ．【解答】解：连接CP 并延长交AB 于F ，由重心的性质得，:2:1CP PF =．//DE AB ，::2:1CD DB CP PF ∴==，:2:3CD CB ∴=， ∴23DE CD AB CB ==， 6AB =，4DE ∴=，故答案为：4．16．一根排水管的截面如图所示，已知水面宽40AB cm =，水的最大深度为8cm ，则排水管的半径为 29 cm ．【解答】解：过点O 作OD AB ⊥，交AB 于点E ，40AB cm =，11402022BE AB cm ∴==⨯=， 在Rt OBE ∆中，8OE OB =-，222OB OE BE ∴=+，即22220(8)OB OB =+-，29OB cm ∴=；故答案为：2917．函数28(y ax ax a =-为常数，且0)a >在自变量x 的值满足23x 剟时，其对应的函数值y的最大值为3-，则a 的值为4 ． 【解答】解：228(4)16y ax ax a x a =-=--，∴函数28(y ax ax a =-为常数，且0)a >的大致函数图象如图所示，在自变量x 的值满足23x 剟时，其对应的函数值y 的最大值为3-， ∴当2x =时，3y =-最大值，即4163a a -=-，解得14a =． 故答案是：14．18．如图是一个摩天轮，它共有8个座舱，依次标为1~8号，摩天轮中心O 的离地高度为50米，摩天轮中心到各座舱中心均相距25米，在运行过程中，当1号舱比3号舱高5米时，1号舱的离地高度为 20 米．【解答】解：如图所示：作BA 、CD 分别垂直于摩天轮水平的直径，A 、D 为垂足，则90BAO ODC ∠=∠=︒，90AOB B ∠+∠=︒，由题意得：90BOC ∠=︒，25OB OC ==，5AB CD =+，90AOB COD ∴∠+∠=︒，B OCD ∴∠=∠，在AOB ∆和DCO ∆中，BAO ODC B OCD OB OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，()AOB DCO AAS ∴∆≅∆，OA CD ∴=，AB OD =，设OA x =，则5AB x =+，在Rt AOB ∆中，由勾股定理得：222(5)25x x ++=，解得：15x =，15520AB ∴=+=（米)，即号舱的离地高度为20米；故答案为：20．三、解答题（共6小题，共46分）：19．有三张分别标有数字2，5，9的卡片，它们的背面都相同．现将它们背面朝上，从中任意抽出一张卡片，不放回，再从剩余的两张卡片里任意抽出一张．（1）请用树状图或列表法表示出所有可能的结果．（2）求两张卡片的数字之和为偶数的概率．【解答】解：（1）根据题意画图如下：共有6种等可能的结果数；（2）共有6种等可能的结果数，抽取的两张卡片的数字之和为偶数的有2种情况，∴两张卡片的数字之和为偶数的概率是：13． 20．如图，在所给的方格纸中，每个小正方形边长都是1，ABC ∆是格点三角形（顶点在方格顶点处）．（1）在图1画格点△111A B C ，使△111A B C 与ABC ∆相似，相似比为2:1．（2）在图2画格点△222A B C ，使△222A B C 与ABC ∆相似，面积比为2:1．【解答】解：（1）如图所示：△111A B C 即为所求：（2）如图所示：△222A B C 即为所求：21．如图，抛物线223y x x =--与x 轴交于A ，B 两点(A 在B 的左侧），顶点为C ．（1）求A ，B 两点的坐标；（2）若将该抛物线向上平移t 个单位后，它与x 轴恰好只有一个交点，求t 的值．【解答】解：（1）当0y =时，2230x x --=，解得13x =，21x =-，所以A 点坐标为(1,0)-，B 点坐标为(3,0)；（2）抛物线223y x x =--向上平移t 个单位后所得抛物线解析式为223y x x t =--+， 则△2(2)4(3)0t =---+=，解得4t =．22．如图，在ABC ∆中，AB AC =，D 是BC 边上的中点，过A ，C ，D 三点的圆交BA 的延长线于点E ，连接EC ．（1）求证：90E ∠=︒；（2）若6AB =，10BC =，求AE 的长．【解答】解：（1）如图，连接AD ，AB AC =，D 是BC 中点，AD BC ∴⊥，即90ADC ADB ∠=∠=︒，∴点A ，C ，D 在以AC 为直径的圆上，90E ∴∠=︒；（2）10BC =， 152BD BC ∴==， B B ∠=∠，90ADB E ∠=∠=︒，BAD BCE ∴∆∆∽， ∴BA BD BC BE =，即65106AE=+， 解得：73AE =． 23．创客联盟的队员想用3D 打印完成一幅边长为4米的正方形作品ABCD ，设计图案如图所示（四周阴影是四个全等的矩形，用材料甲打印；中心区是正方形A B C D ''''，用材料乙打印）．在打印厚度保持相同的情况下，两种材料的消耗成本如下表设矩形的较短边AH 的长为x 米，打印材料的总费用为y 元． （1）A D ''的长为 42x - 米（用含x 的代数式表示）；（2）求y 关于x 的函数解析式；（3）当中心区的边长不小于3时，预备材料的购买资金700元够用吗？请利用函数的增减性来说明理由．【解答】解：（1）AH GD x ='=，4AD =，42A D x ∴''=-； 故答案为：42x -；（2）y 关于x 的函数解析式为：22604(4)30(42)120480480y x x x x x =⨯⨯-+⨯-=-++；（3）当中心区的边长不小于3米时，423x ∴-…，解得：0.5x …，2120480480y x x =-++，1200a =-<，22b a-=， ∴当0.5x …时，y 随x 增大而增大， 所以当12x =时，690700y =<， 所以当中心区的边长不小于3米时，预备材料的购买资金700元够用．24．如图，在平面直角坐标系中，(3,4)A ，(5,0)B ，连结AO ，AB ．点C 是线段AO 上的动点（不与A，O重合），连结BC，以BC为直径作H，交x轴于点D，交AB于点E，连结CD，CE，过E作EF x⊥轴于F，交BC于G．（1）AO的长为5，AB的长为（直接写出答案）（2）求证：ACE BEF∽；∆∆（3）若圆心H落在EF上，求BC的长；（4）若CEG∆是以CG为腰的等腰三角形，求点C的坐标．【解答】解：（1）(3,4)A，(5,0)B．∴=，5OA5OB=，AB==．故答案为：5；．（2）如图1中，==，5OA OB∴∠=∠，A EBFBC是直径，∴∠=∠=︒，BEC AEC90EF OB⊥，∴∠=︒，90EFBAEC EFB∴∠=∠=︒，90∴∆∆∽．ACE BEF（3）如图2中，当GC GE=时，点G与点H重合，∴==，GE GB GCGEB EBG∴∠=∠，∠+∠=︒，90GEB ABO∴∠+∠=︒，EBG ABO90=，OA OB∴∠=∠，A OBA∴∠+∠=︒，90A EBG∴∠=︒，90ACB∴⊥，BC AOOC OB AOB∴=∠=，cos3BC∴===；4（4）①如图2中，当GC GE=时，点G与点H重合，∴==，GE GB GCGEB EBG∴∠=∠，∠+∠=︒，90GEB ABO∴∠+∠=︒，EBG ABO90=，OA OBA OBA ∴∠=∠，90A EBG ∴∠+∠=︒，90ACB ∴∠=︒，BC AO ∴⊥，cos 3OC OB AOB ∴=∠=，9(5C ∴，12)5． ②如图3中，当CE CG =时，作AK OB ⊥于K ．设4CD k =，3OD k =．CE CG =，CEG CGE BGF ∴∠=∠=∠，90CEG BEF ∠+∠=︒，90BGF CBD ∠+∠=︒， CBD BEF ∴∠=∠，EF OB ⊥，AK PB ⊥，//EF AK ∴，BEF BAK ∴∠=∠，CBD BAK ∴∠=∠，90CDB AKB ∠=∠=︒，CBD BAK ∴∆∆∽， ∴CD BD BK AK =， ∴45324k k -=， 511k ∴=，15(11C ，20)11．。

2019-2020学年浙江省温州市九年级（上）期末数学试卷一、选择题（共10小题）.1．（3分）已知O 的半径为5cm ，点P 在O 上，则OP 的长为( )A ．4cmB ．5cmC ．8cmD ．10cm 2．（3分）若52x y =，则x y y -的值为( ) A ．52 B ．25 C ．32 D ．35- 3．（3分）将抛物线22y x =-向上平移1个单位后所得新抛物线的表达式为( )A ．21y x =-B ．23y x =-C ．2(1)2y x =+-D ．2(1)2y x =--4．（3分）如图，在56⨯的方格纸中，画有格点EFG ∆，下列选项中的格点，与E ，G 两点构成的三角形中和EFG ∆相似的是( )A ．点AB ．点BC ．点CD ．点D5．（3分）某单位进行内部抽奖，共准备了100张抽奖券，设一等奖10个，二等奖20个，三等奖30个．若每张抽奖券获奖的可能性相同，则1张抽奖券中奖的概率是( )A ．0.1B ．0.2C ．0.3D ．0.66．（3分）如图，ACB ∠是O 的圆周角，若O 的半径为10，45ACB ∠=︒，则扇形AOB 的面积为( )A ．5πB ．12.5πC ．20πD ．25π7．（3分）已知点(3,)A a -，(2,)B b -，(1,)C c 均在抛物线23(2)y x k =++上，则a ，b ，c 的大小关系是( )A ．c a b <<B ．a c b <<C ．b a c <<D ．b c a <<8．（3分）如图，AD 是O 的直径，以A 为圆心，弦AB 为半径画弧交O 于点C ，连结BC交AD 于点E ，若3DE =，8BC =，则O 的半径长为( )A ．256B ．5C ．163D ．2539．（3分）有一等腰三角形纸片ABC ，AB AC =，裁剪方式及相关数据如图所示，则得到的甲、乙、丙、丁四张纸片中，面积最大的是( )A ．甲B ．乙C ．丙D ．丁10．（3分）如图，抛物线2()5y x m =-++交x 轴于点A ，B ，将该抛物线向右平移3个单位后，与原抛物线交于点C ，则点C 的纵坐标为( )A ．52B ．114C ．3D ．134二、填空题（本题有8个小题，每小题3分，共24分）11．（3分）抛物线29y x =-与y 轴的交点坐标为 ．12．（3分）如图，是用卡钳测量容器内径的示意图．量得卡钳上A ，D 两端点的距离为4cm ，25AO DO OC OB ==，则容器的内径BC 的长为 cm ．13．（3分）如图，已知AB 是半圆O 的直径，20BAC ∠=︒，D 是弧AC 上任意一点，则D ∠的度数是 ．14．（3分）如图，ABC ∆绕点A 逆时针旋转得到△AB C ''，点C 在AB '上，点C 的对应点C '在BC 的延长线上，若80BAC '∠=︒，则B ∠= 度．15．（3分）如图，正五边形ABCDE 内接于O ，若O 的半径为10，则AB 的长为 ．16．（3分）如图，在ABC ∆中，90ABC ∠=︒，6AB =，4BC =，P 是ABC ∆的重心，连结BP ，CP ，则BPC ∆的面积为 ．17．（3分）已知二次函数243y x x =-+，当5a x a +时，函数y 的最小值为1-，则a 的取值范围是18．（3分）如图，AB 是半圆O 的直径，D 是半圆O 上一点，C 是BD 的中点，连结AC 交BD 于点E ，连结AD ，若4BE DE =，6CE =，则AB 的长为 ．三、解答题（本题有6小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程）19．（6分）甲乙两人参加一个幸运挑战活动，活动规则是：一个布袋里装有3个只有颜色不同的球，其中2个红球，1个白球．甲从布袋中摸出一个球，记下颜色后放回，搅匀，乙再摸出一个球，若颜色相同，则挑战成功．（1）用列表法或树状图法，表示所有可能出现的结果．（2）求两人挑战成功的概率．20．（6分）我们把端点都在格点上的线段叫做格点线段．如图，在77⨯的方格纸中，有一格点线段AB ，按要求画图．（1）在图1中画一条格点线段CD 将AB 平分．（2）在图2中画一条格点线段EF ．将AB 分为1:3．21．（6分）如图，在平面直角坐标系中，抛物线2122y x x a =-++交x 轴于点A ，B ，交y 轴于点C ，点A 的横坐标为2-．（1）求抛物线的对称轴和函数表达式．（2）连结BC 线段，BC 上有一点D ，过点D 作x 轴的平行线交抛物线于点E ，F ，若6EF =，求点D 的坐标．22．（8分）如图，四边形ABCD内接于O，点E在CB的延长线上，BA平分EBD∠，AE AB=．（1）求证：AC AD=．（2）当32AEEB=，6AD=时，求CD的长．23．（8分）总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，甲店一天可售出20件，每件盈利40元；乙店一天可售出32件，每件盈利30元．经调查发现，每件衬杉每降价1元，甲、乙两家店一天都可多售出2件．设甲店每件衬衫降价a元时，一天可盈利1y元，乙店每件衬衫降价b元时，一天可盈利2y元．（1）当5a=时，求1y的值．（2）求2y关于b的函数表达式．（3）若总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和最大，最大是多少元？24．（12分）如图，在矩形ABCD中，6AB=，8BC=，点E，F分别在边BC，AB上，2AF BE==，连结DE，DF．动点M在EF上从点E向终点F匀速运动，同时，动点N 在射线CD上从点C沿CD方向匀速运动，当点M运动到EF的中点时，点N恰好与点D重合，点M到达终点时，M，N同时停止运动．（1）求EF的长．（2）设CN x=，求y关于x的函数表达式，并写出自变量x的取值范围．=，EM y（3）连结MN，当MN与DEF∆的一边平行时，求CN的长．参考答案一、选择题（本题有10小题，每小题3分，共30分.每小题只有一个选项是正确的，不选、多选、错选均不给分）1．（3分）已知O 的半径为5cm ，点P 在O 上，则OP 的长为( )A ．4cmB ．5cmC ．8cmD ．10cm 解：点P 在O 上，5OP r cm ∴==， 故选：B ．2．（3分）若52x y =，则x y y -的值为( ) A ．52 B ．25 C ．32 D ．35- 解：52x y =， ∴531122x y x y y -=-=-=． 故选：C ．3．（3分）将抛物线22y x =-向上平移1个单位后所得新抛物线的表达式为( )A ．21y x =-B ．23y x =-C ．2(1)2y x =+-D ．2(1)2y x =-- 解：将抛物线22y x =-向上平移1个单位后所得新抛物线的表达式为221y x =-+，即21y x =-．故选：A ．4．（3分）如图，在56⨯的方格纸中，画有格点EFG ∆，下列选项中的格点，与E ，G 两点构成的三角形中和EFG ∆相似的是( )A ．点AB ．点BC ．点CD ．点D解：观察图形可得EFG ∆中，直角边的比为12FG EF =， 观各选项，51225EG DG ==，只有D 选项三角形符合，与所给图形的三角形相似． 故选：D ．5．（3分）某单位进行内部抽奖，共准备了100张抽奖券，设一等奖10个，二等奖20个，三等奖30个．若每张抽奖券获奖的可能性相同，则1张抽奖券中奖的概率是( )A ．0.1B ．0.2C ．0.3D ．0.6解：共准备了100张抽奖券，设一等奖10个，二等奖20个，三等奖30个．1∴张抽奖券中奖的概率是1020300.6100++=， 故选：D ．6．（3分）如图，ACB ∠是O 的圆周角，若O 的半径为10，45ACB ∠=︒，则扇形AOB 的面积为( )A ．5πB ．12.5πC ．20πD ．25π解：45ACB ∠=︒，90AOB ∴∠=︒， 半径为10，∴扇形AOB 的面积为：2901025360ππ⨯=， 故选：D ．7．（3分）已知点(3,)A a -，(2,)B b -，(1,)C c 均在抛物线23(2)y x k =++上，则a ，b ，c 的大小关系是( )A ．c a b <<B ．a c b <<C ．b a c <<D ．b c a << 解：函数的对称轴为：2x =-，30a =>，故开口向上，1x =比3x =-离对称轴远，故c 最大，b 为函数最小值，故选：C ．8．（3分）如图，AD 是O 的直径，以A 为圆心，弦AB 为半径画弧交O 于点C ，连结BC 交AD 于点E ，若3DE =，8BC =，则O 的半径长为( )A ．256B ．5C ．163D ．253 解：由作法得AC AB =，∴AB AC =，ADB ABE ∴∠=∠，AB 为直径，AD BC ∴⊥，142BE CE BC ∴===，90BEA BED ∠=∠=︒， 而BDE ABE ∠=∠，Rt ABE Rt BDE ∴∆∆∽，::BE DE AE BE ∴=，即4:3:4AE =，163AE ∴=， 1625333AD AE DE ∴=+=+=， O ∴的半径长为256． 故选：A ．9．（3分）有一等腰三角形纸片ABC ，AB AC =，裁剪方式及相关数据如图所示，则得到的甲、乙、丙、丁四张纸片中，面积最大的是( )A ．甲B ．乙C ．丙D ．丁 解：AD BC ⊥，AB AC =，527BD CD ∴==+=，213AD =+=， 1217322ABD ACD S S ∆∆∴==⨯⨯=//EF AD ， EBF ABD ∴∆∆∽，∴2525()749ABD S S ∆==甲， 7514S ∴=甲， 2175362147S ∴=-=乙， 同理224()39ACD S S ∆==丙， 429S ∴=丙， 2142952918S ∴=-=丁， 95751814>， ∴面积最大的是丁，故选：D ．10．（3分）如图，抛物线2()5y x m =-++交x 轴于点A ，B ，将该抛物线向右平移3个单位后，与原抛物线交于点C，则点C的纵坐标为()A．52B．114C．3D．134解：将抛物线2()5y x m=-++向右平移3个单位后得到2(3)5y x m=-+-+，根据题意得：22()5(3)5y x my x m⎧=-++⎨=-+-+⎩，解得：32114x my⎧=-⎪⎪⎨⎪=⎪⎩，∴交点C的坐标为3(2m-，11)4，故选：B．二、填空题（本题有8个小题，每小题3分，共24分）11．（3分）抛物线29y x=-与y轴的交点坐标为(0,9)-．解：令0x=，299y x=-=-，故答案为：(0,9)-12．（3分）如图，是用卡钳测量容器内径的示意图．量得卡钳上A，D两端点的距离为4cm，25AO DOOC OB==，则容器的内径BC的长为10cm．解：如图，连接AD，BC，25AO DO OC OB ==，AOD BOC ∠=∠， AOD BOC ∴∆∆∽，∴25AD AO BC CO ==， 又4AD cm =，5102BC AD cm ∴==． 故答案是：10cm ．13．（3分）如图，已知AB 是半圆O 的直径，20BAC ∠=︒，D 是弧AC 上任意一点，则D ∠的度数是 110︒ ．解：AB 是半圆O 的直径90ACB ∴∠=︒902070ABC ∴∠=︒-︒=︒18070110D ∴∠=︒-︒=︒故答案是：110︒．14．（3分）如图，ABC ∆绕点A 逆时针旋转得到△AB C ''，点C 在AB '上，点C 的对应点C '在BC 的延长线上，若80BAC '∠=︒，则B ∠= 30 度．解：ABC ∆绕点A 逆时针旋转得到△AB C ''，C AB CAB ∴∠''=∠，AC AC '=，80BAC '∠=︒，1402C AB CAB C AB ∴∠''=∠=∠'=︒， 70ACC ∴∠'=︒，30B ACC CAB ∴∠=∠'-∠=︒，故答案为：30．15．（3分）如图，正五边形ABCDE 内接于O ，若O 的半径为10，则AB 的长为 4π ．解：如图所示：连接OA 、OB ．O 为正五边形ABCDE 的外接圆，O 的半径为5，360725AOB ︒∴∠==︒， ∴AB 的长为：72104180ππ⨯=． 故答案为4π．16．（3分）如图，在ABC ∆中，90ABC ∠=︒，6AB =，4BC =，P 是ABC ∆的重心，连结BP ，CP ，则BPC ∆的面积为 4 ．解：ABC ∆的面积11641222S AB BC =⨯=⨯⨯=， 延长BP 交AC 于点E ，则E 是AC 的中点，且23BP BE =（证明见备注），BEC ∆的面积162S ==，23BP BE =， 则BPC ∆的面积23BEC =∆的面积4=， 故答案为4．备注：重心到顶点的距离与重心到对边中点的距离之比为2:1，例：已知：ABC ∆，E 、F 是AB ，AC 的中点．EC 、FB 交于G ．求证：12EG CG = 证明：过E 作//EH BF 交AC 于H ． AE BE =，//EH BF ，12AH HF AF ∴==， 又AF CF =，12HF CF ∴=， 1:2HF CF ∴=， //EH BF ，1::2EG CG HF CF ∴==， 12EG CG ∴=． 17．（3分）已知二次函数243y x x =-+，当5a x a +时，函数y 的最小值为1-，则a 的取值范围是 32a -解：二次函数2243(2)1y x x x =-+=--，∴对称轴为直线2x =，当25a a <<+时，则在5a x a +范围内，2x =时有最小值1-，当2a 时，则在5a x a +范围内，x a =时有最小值1-，2431a a ∴-+=-，解得2a =，当52a +时，则在5a x a +范围内，5x a =+时有最小值1-，2(5)4(5)31a a ∴+-++=-，解得3a =-，a ∴的取值范围是32a -，故答案为32a -．18．（3分）如图，AB 是半圆O 的直径，D 是半圆O 上一点，C 是BD 的中点，连结AC 交BD 于点E ，连结AD ，若4BE DE =，6CE =，则AB 的长为 410 ．解：如图，连接OC 交BD 于K ．CD BC =，OC BD ∴⊥，4BE DE =，∴可以假设DE k =．4BE k =，则 2.5DK BK k ==， 1.5EK k =，AB 是直径，90ADK DKC ACB ∴∠=∠=∠=︒，//AD CK ∴，::AE EC DE EK ∴=，:6:1.5AE k k ∴=，4AE ∴=，ECK EBC ∆∆∽，2EC EK EB∴=，36 1.54k k∴=⨯，k>，6k∴=，229636215BC BE EC∴=-=-=，222210(215)410AB AC BC∴=+=+=．故答案为410．三、解答题（本题有6小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程）19．（6分）甲乙两人参加一个幸运挑战活动，活动规则是：一个布袋里装有3个只有颜色不同的球，其中2个红球，1个白球．甲从布袋中摸出一个球，记下颜色后放回，搅匀，乙再摸出一个球，若颜色相同，则挑战成功．（1）用列表法或树状图法，表示所有可能出现的结果．（2）求两人挑战成功的概率．解：（1）用列表法表示所有可能出现的结果如下：（2）共有9种等可能出现的结果，其中颜色相同的有5种，()5 9P∴=颜色相同，答：获胜的概率为59．20．（6分）我们把端点都在格点上的线段叫做格点线段．如图，在77⨯的方格纸中，有一格点线段AB，按要求画图．（1）在图1中画一条格点线段CD将AB平分．（2）在图2中画一条格点线段EF．将AB分为1:3．解：（1）如图，线段CD 即为所求．（2）如图，线段EF 即为所求，注意有两种情形．21．（6分）如图，在平面直角坐标系中，抛物线2122y x x a =-++交x 轴于点A ，B ，交y 轴于点C ，点A 的横坐标为2-．（1）求抛物线的对称轴和函数表达式．（2）连结BC 线段，BC 上有一点D ，过点D 作x 轴的平行线交抛物线于点E ，F ，若6EF =，求点D 的坐标．解：（1）A 点的横坐标为2-，(2,0)A ∴-，点A 在抛物线2122y x x a =-++上， 240a ∴--+=，解得：6a =，∴函数的解析式为：21262y x x =-++， ∴对称轴为22122()2b x a =-=-=⨯-；（2）(2,0)A -，对称轴为2x =，∴点B 的坐标为(6,0)，∴直线BC 的解析式为6y x =-+，点D 在BC 上，∴设点D 的坐标为(,6)m m -+，∴点E 和点F 的纵坐标为6m -+，212662y x x m ∴=-++=-+，解得：2x =±2(2EF ∴=--=6EF =，6∴=，解得： 2.5m =，∴点D 的坐标为(2.5,3.5)．22．（8分）如图，四边形ABCD内接于O，点E在CB的延长线上，BA平分EBD∠，AE AB=．（1）求证：AC AD=．（2）当32AEEB=，6AD=时，求CD的长．【解答】（1）证明：BA平分EBD∠，ABE ABD∴∠=∠，ABE ADC∠=∠，ABD ACD∠=∠，ACD ADC∴∠=∠，AC AD∴=；（2）解：AE AB=，E ABE∴∠=∠，E ABE ACD ADC∴∠=∠=∠=∠，ABE ACD∴∆∆∽，∴32AE ADBE CD==，226433CD AD∴==⨯=．23．（8分）总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，甲店一天可售出20件，每件盈利40元；乙店一天可售出32件，每件盈利30元．经调查发现，每件衬杉每降价1元，甲、乙两家店一天都可多售出2件．设甲店每件衬衫降价a 元时，一天可盈利1y 元，乙店每件衬衫降价b 元时，一天可盈利2y 元．（1）当5a =时，求1y 的值．（2）求2y 关于b 的函数表达式．（3）若总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和最大，最大是多少元？解：（1）由题意可得，1(40)(202)y a a =-+，当5a =时，1(405)(2025)1050y =-⨯+⨯=，即当5a =时，1y 的值是1050；（2）由题意可得，22(30)(322)228960y b b b b =-+=-++，即2y 关于b 的函数表达式为22228960y b b =-++；（3）设两家下降的价格都为x 元，两家的盈利和为w 元，222(40)(202)(228960)48817604(11)2244w x x x x x x x =-++-++=-++=--+， ∴当11x =时，w 取得最大值，此时2244w =，答：每件衬衫下降11元时，两家分店一天的盈利和最大，最大是2244元．24．（12分）如图，在矩形ABCD 中，6AB =，8BC =，点E ，F 分别在边BC ，AB 上，2AF BE ==，连结DE ，DF ．动点M 在EF 上从点E 向终点F 匀速运动，同时，动点N 在射线CD 上从点C 沿CD 方向匀速运动，当点M 运动到EF 的中点时，点N 恰好与点D 重合，点M 到达终点时，M ，N 同时停止运动．（1）求EF 的长．（2）设CN x =，EM y =，求y 关于x 的函数表达式，并写出自变量x 的取值范围．（3）连结MN ，当MN 与DEF ∆的一边平行时，求CN 的长．解：（1）四边形ABCD是矩形，90B∴∠=︒，6AB CD==，8AD BC==，2AF BE==，624BF∴=-=，22224225EF BF BE∴=+=+=．（2）由题意：12EF EM CD CN=，∴56yx=5(012)6y x x∴=．（3）如图31-中，延长FE交DC的延长线于H．EFB EHC∆∆∽，∴EF BE BF EH EC CH ==， ∴25246EH CH ==， 65EH ∴=，12CH =， 当//MN DF 时，HM HN HF BD =， ∴65121885yx ++=， 56y x =， 解得125x =，这种情形不存在．如图32-中，当//MN DE 时，EH DH EM DN=，∴65186x =-， 5y x =， 解得12x =，综上所述，满足条件的CN 的值为125或12．。

2019-2020学年浙教版九年级上期末考试数学试卷一．选择题（共10小题，满分40分，每小题4分）1．下列抛物线中，与y轴交点坐标为（0，3）的是（）A．y＝（x﹣3）2B．y＝x2﹣3C．y＝2x2﹣3x D．y＝x2﹣2x+3 2．如图所示是一个旋转对称图形，若将它绕自身中心旋转一定角度之后不能与原图重合，则这个角度可能是（）A．60°B．90°C．120°D．180°3．已知一个扇形的弧长为3π，所含的圆心角为120°，则半径为（）A．9B．3C．D．4．把抛物线y＝﹣x2先向左平移1个单位，再向下平移2个单位，得到的抛物线的表达式是（）A．y＝﹣（x+1）2+2B．y＝﹣（x+1）2﹣2C．y＝﹣（x﹣1）2﹣2D．y＝（x+1）2﹣25．有两辆车按1，2编号，方方和成成两人可以任意选坐一辆车．则两人同坐1号车的概率为（）A．B．C．D．6．已知点（﹣2，y1），（，y2），（，y3）在函数y＝﹣（x﹣1）2的图象上，则y1，y2，y3的大小关系是（）A．y1＞y2＞y3B．y2＞y1＞y3C．y2＞y3＞y1D．y3＞y1＞y27．如图，已知在△ABC中，AB＝14，BC＝12，AC＝10，D是AC上一点，过点D画一条直线l，把△ABC分成两部分，使其中的一个三角形与△ABC相似，这样的直线有几条（）A．2B．3C．3或4D．48．甲、乙两人同时从A地出发，步行15km到B地，甲比乙每小时多走1km，结果甲比乙早到半小时，两人每小时各走几千米？设甲每小时走xkm，则可列出的方程为（）A．B．C．D．9．已知反比例函数的图象经过点P（4，﹣1），则该反比例函数的图象所在的象限是（）A．第一、二象限B．第一、三象限C．第二、三象限D．第二、四象限10．如图，在矩形ABCD中，AB＝3，BC＝5，点E在对角线AC上，连接BE，作EF⊥BE，垂足为E，直线EF交线段DC于点F，则＝（）A．B．C．D．二．填空题（共6小题，满分30分，每小题5分）11．（5分）醴陵市农科站在相同条件下经试验发现蚕豆种子的发芽率为97.5%，请估计醴陵地区1000斤蚕豆种子中不能发芽的大约有斤．12．（5分）若△ABC∽△A′B′C′，∠A＝50°，∠C＝110°，则∠B′的度数为．13．（5分）如图，隧道的截面是抛物线型，抛物线的解析式为y＝﹣2+4．隧道是单行道（车从正中间通过），为安全考虑，车顶与隧道顶部的垂直距离不少于0.5m，若货运汽车的宽为2米，则车安全通过隧道的限高为米．。

浙江瑞安市集云实验学校、安阳实验中学等五校2020届九年级上学期期末考试语文试题及答案部编人教版九年级总复习学年第一学期九年级语文卷.12亲爱的同学：欢迎参加考试！请你认真审题，积极思考，细心答题，发挥出最佳水平。

答题时，请注意以下几点：1.全卷共6页，有3大题，18小题。

满分150分（含书写5分）。

考试时间120分钟。

2.答案必须写在答题纸相应的位置上，写在试题卷、草稿纸上均无效。

祝你成功！一、积累（16分）1．根据拼音写出相应的汉字。

（4分）2．古诗小组积累卡。

根据提示，完成填空。

（12分）对偶：前后两句字数等，结构相同意对称。

写景叙事语言简，论人评事情意浓。

出处诗句赏析刘长卿《长沙过贾谊宅》秋草独寻人去后，①。

斜阳衰草，寒林空寂，斯人已去，唯有嗟叹。

许浑《咸阳城东楼》②，③。

溪云乍起，夕阳沉落；山雨将至，风声满楼。

萧条苍凉，危机四伏。

温庭筠《商山早行》槲叶落山路，④。

槲叶随地飘洒，枳花明丽可爱，却无法抑止思乡的愁绪。

欧阳修《醉翁亭记》野芳发而幽香，⑤。

野花的幽香，繁茂的绿荫，野趣无尽。

用典：引用过去之有关人、地、事、物之史实，或语言文字，怀古伤今，抒发了诗人情感。

出处诗句赏析李白《行路难》闲来垂钓碧溪上，⑥。

引用姜太公和伊尹的典故，表达了⑦。

刘禹锡《酬乐天扬州初逢席上见赠》⑧，⑨。

借向秀《思旧赋》和烂柯人的典故，寄寓了作者还乡时的怅惘之情。

李商隐《无题》蓬山此去无多路，⑩。

借青鸟传信，寄思念之情，惆怅伤感。

杜甫《蜀相》.，.。

借三顾茅庐的典故，表达了对诸葛亮雄才大略，忠心报国的赞颂之情。

二、阅读（69分）（一）《水浒传》小组探究卡（8分）探究主题《水浒传》的个性化人物语言探究方法对比探究参考文献金圣叹《第五才子书施耐庵水浒传》横向对比3.金圣叹评《水浒》人物语言：“一样人，便还他一样说话”。

以下是众好汉初见宋江时说的话，根据小说内容，将序号填入相应的横线处。

（3分）A.“这黑汉子是谁?”B.“小人‘有眼不识泰山’！一时冒渎兄长，望乞恕罪！”C.“天幸今日甚风吹得到此，大慰平生渴仰之念，多幸！多幸！”①柴进▲②李逵▲③武松▲纵向对比话语摘抄A“不合吃着他的请受，权且让他一次。

2019-2020学年浙江省温州市九年级（上）期末数学试卷一、选择题（本题有10小题，每小题3分，共30分，每小题只有一个选项是正确的，不选、多选错选均不给分）1．（3分）下列选项中的事件，属于随机事件的是（）A．在一个只装有黑球的袋中，摸出红球B．两个正数相加，和是正数C．一打开电视机，正在播新闻D．在一个只装有黑球的袋中，摸出黑球2．（3分）抛物线y＝x2﹣9与y轴的交点坐标是（）A．（﹣9，0）B．（0，﹣9）C．（3，0）D．（0，3）3．（3分）如图，在2×3的方格中，画有格点△ABC，下列选项的方格中所画格点三角形（阴影部分）与△ABC相似的是（）A．B．C．D．4．（3分）如图，在△ABC中，∠C＝90°，AB＝5，AC＝4，D，E分别是AC，AB的中点，若作半径为2的⊙D，则下列选项中的点在⊙D外的是（）A．点A B．点B C．点C D．点E5．（3分）如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC．若AD＝3BD，△ADE的周长为3，则△ABC的周长为（）A ．4B ．6C ．9D ．126．（3分）如图，在3×3的方格中，已有两个小正方形被涂黑，若在其余空白小正方形中任选一个涂黑，则所得图案是一个轴对称图形的概率是（ ）A ．17B ．27C ．37D ．47 7．（3分）已知点A （﹣2，a ），B （﹣1，b ），C （3，c ）均在抛物线y ＝﹣2（x +1）2+3上，则a ，b ，c 的大小关系为（ ）A ．a ＜c ＜bB ．b ＜a ＜cC ．c ＜a ＜bD ．a ＜b ＜c8．（3分）如图，圆上有两点A ，B ，连接AB ，分别以A ，B 为圆心，AB 的长为半径画弧，两弧相交于点C ，D ，CD 交AB 于点E ，交AB̂于点F ．若EF ＝1，AB ＝6，则该圆的半径长是（ ）A ．4B ．5C ．6D ．109．（3分）如图，P 是矩形ABCD 内一点，连结P 与矩形ABCD 各顶点，矩形EFGH 各顶点分别在边AP ，BP ，CP ，DP 上，已知AE ＝2EP ，EF ∥AB ，图中两块阴影部分的面积和为S ．则矩形ABCD 的面积为（ ）A．4S B．6S C．12S D．18S10．（3分）如图，在坐标系网格中，过点B的抛物线顶点为A，且点A，B，C，D，E，F，O都在格点上，则该抛物线还经过下列选项中的（）A．点C B．点D C．点E D．点F二、填空题（本题有8个小题，每小题3分，共24分）11．（3分）已知xy =43，则x−yy=．12．（3分）将抛物线y＝x2+2向上平移1个单位后所得新抛物线的表达式为．13．（3分）如图，AB∥CD∥EF，点E，F分别在线段AD，BC上，已知BF＝4，CF＝6，AE＝5，则DE的长为．14．（3分）如图，在一个半径为3的圆中，若圆周角∠ABC为30°，则AĈ的长为．15．（3分）如图，AB是半圆O的直径，点D，E在半圆上，∠DOE＝100°，点C在DÊ上，连接CD，CE，则∠DCE等于度．16．（3分）如图，两个完全相同的正五边形ABCDE，AFGHM的边DE，MH在同一直线上，且有一个公共顶点A，若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合，则x的最小值为．17．（3分）如图1，G为△ABC纸片的重心，DG∥AC交BC于点D，连结BG，剪去△BGD 纸片，剩余部分纸片如图2所示，若原△ABC纸片面积为5，则图2纸片的面积为．18．（3分）如图，四边形ABDC内接于半圆O，AB为直径，AD平分∠CAB，AB﹣AC＝4，AD＝3√7，作DE⊥AB于点E，则BE的长为，AC的长为．三、解答题（本题有6小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程）19．（6分）有4张卡片，正面分别写上1，2，3，4，它们的背面都相同．现将它们背面朝上，先从中任意摸出一张，卡片不放回，再任意摸出一张．（1）请用树状图或列表法表示出所有可能的结果．（2）求摸出的两张卡片上的数之和大于5的概率．20．（6分）如图，△ABC内接于⊙O，请用直尺和圆规按要求作图（保留作图痕迹）．（1）在图1中画出一个圆心角，所作角的度数是∠ACB的2倍．（2）在图2中画出一个圆周角，所作角的度数是∠ACB的2倍．21．（6分）已知抛物线y＝x2﹣4x+a+1．（1）若抛物线经过点（3，5），求该抛物线的表达式．（2）若该抛物线与x轴有且只有一个交点，求a的值．22．（8分）如图，在Rt△ABC中，∠B＝90°，BC＞AB，在BC边上取点D，使AB＝BD，构造正方形ABDE，DE交AC于点F，作EG⊥AC交AC于点G，BC于点H．（1）求证：△AEF≌△EDH．（2）若AB＝3，DH＝2DF，求BC的长．23．（8分）小张准备给长方形客厅铺设瓷砖，已知客厅长AB＝8m，宽BC＝6m，现将其划分成一个长方形EFGH区域I和环形区域Ⅱ，区域Ⅰ用甲、乙瓷砖铺设，其中甲瓷砖铺设成的是两个全等的菱形图案，区域Ⅱ用丙瓷砖铺设，如图所示，已知N是GH中点，点M在边HE上，HN＝3HM，设HM＝x（m）．（1）用含x的代数式表示以下数量．铺设甲瓷砖的面积为m2．铺设丙瓷砖的面积为m2．（2）若甲、乙、丙瓷砖单价分别为300元/m2，200元/m2，100元/m2，且EF≥FG+2，铺设好整个客厅，三种瓷砖总价至少需要多少钱？24．（12分）如图，在矩形BCD中，AB＝3，AD＝8，O为AD中点，P是线段AO上一动点，以O为圆心，OP为半径作⊙O分别交BO及BO延长线于点E，F，延长AE交BC 于点H．（1）当OP＝2时，求BH的长．（2）当AH交⊙O于另一点G时，连接FG，DF，作DM⊥BF于点M，求证：△EFG ∽△FDM．（3）连结HO，当△EHO是直角三角形时，求OP的长．2018-2019学年浙江省温州市九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分，每小题只有一个选项是正确的，不选、多选错选均不给分）1．（3分）下列选项中的事件，属于随机事件的是（）A．在一个只装有黑球的袋中，摸出红球B．两个正数相加，和是正数C．一打开电视机，正在播新闻D．在一个只装有黑球的袋中，摸出黑球【分析】根据必然事件、不可能事件、随机事件的概念可区别各类事件．【解答】解：A、在一个只装有黑球的袋中，摸出红球是不可能事件，错误；B、两个正数相加，和是正数是必然事件，错误；C、一打开电视机，正在播新闻是随机事件，正确；D、在一个只装有黑球的袋中，摸出黑球是必然事件，错误；故选：C．【点评】本题考查了随机事件，解决本题需要正确理解必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件．不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．2．（3分）抛物线y＝x2﹣9与y轴的交点坐标是（）A．（﹣9，0）B．（0，﹣9）C．（3，0）D．（0，3）【分析】令x＝0，求出y的值，然后写出交点坐标即可．【解答】解：x＝0时，y＝﹣9，所以，抛物线与y轴的交点坐标为（0，﹣9）．故选：B．【点评】本题考查了二次函数图象上点的坐标特征，熟练掌握二次函数图象与坐标轴的交点的求解方法是解题的关键．3．（3分）如图，在2×3的方格中，画有格点△ABC，下列选项的方格中所画格点三角形（阴影部分）与△ABC相似的是（）A．B．C．D．【分析】利用两组对应边的比相等且夹角对应相等的两个三角形相似对各选项进行判断．【解答】解：∠ACB＝90°，AC＝2，BC＝1，AC：BC＝2，A选项中，三条线段的长为√2，2√2，√10，因为（√2）2+（2√2）2＝（√10）2，此三角形为直角三角形，长直角边与短直角边的比为2，所以A选项的方格中所画格点三角形（阴影部分）与△ABC相似；而B选项中长直角边与短直角边的比为3，C、D选项中的两直角边的比为1：1．故选：A．【点评】本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．4．（3分）如图，在△ABC中，∠C＝90°，AB＝5，AC＝4，D，E分别是AC，AB的中点，若作半径为2的⊙D，则下列选项中的点在⊙D外的是（）A．点A B．点B C．点C D．点E【分析】分别求出AD、CD、BD、ED的长，根据点与圆的位置关系的判断方法进行判断即可．【解答】解：∵∠C＝90°，AB＝5，AC＝4，∴BC＝3，∵且点D，E分别是AC，AB的中点，∴CD ＝AD ＝2，BE ＝AE =52，DE =12BC =32，∴BD =√22+32=√13，∵半径为2，∴点B 在⊙C 外，∴点E 在⊙C 内，∴点A ，C 在⊙C 上，故选：B ．【点评】本题考查的是点与圆的位置关系的判断．关键要记住若半径为r ，点到圆心的距离为d ，则有：当d ＞r 时，点在圆外；当d ＝r 时，点在圆上，当d ＜r 时，点在圆内．5．（3分）如图，在△ABC 中，点D ，E 分别在边AB ，AC 上，DE ∥BC ．若AD ＝3BD ，△ADE 的周长为3，则△ABC 的周长为（ ）A ．4B ．6C ．9D ．12【分析】证明△ADE ∽△ABC ，根据相似三角形的周长比等于相似比计算即可．【解答】解：∵AD ＝3BD ，∴AD AB =34， ∵DE ∥BC ，∴△ADE ∽△ABC ，∴△ADE 的周长△ABC 的周长=34， ∵△ADE 的周长为3，∴△ABC 的周长＝4，故选：A ．【点评】本题考查的是相似三角形的判定和性质，掌握相似三角形的周长比等于相似比是解题的关键．6．（3分）如图，在3×3的方格中，已有两个小正方形被涂黑，若在其余空白小正方形中任选一个涂黑，则所得图案是一个轴对称图形的概率是（ ）A ．17B ．27C ．37D ．47 【分析】在7个空白处分别涂黑，再根据轴对称图形的对应进行判断，然后根据概率公式求解．【解答】解：在其余空白小正方形中任选一个涂黑，则所得图案是一个轴对称图形的概率=37．故选：C ．【点评】本题考查了概率公式：随机事件A 的概率P （A ）＝事件A 可能出现的结果数除以所有可能出现的结果数．也考查了轴对称图形．7．（3分）已知点A （﹣2，a ），B （﹣1，b ），C （3，c ）均在抛物线y ＝﹣2（x +1）2+3上，则a ，b ，c 的大小关系为（ ）A ．a ＜c ＜bB ．b ＜a ＜cC ．c ＜a ＜bD ．a ＜b ＜c 【分析】根据二次函数的性质得到抛物线y ＝﹣2（x +1）2+3的开口向下，对称轴为直线x ＝﹣1，然后根据三个点离对称轴的远近判断函数值a 、b 、c 的大小．【解答】解：∵抛物线y ＝﹣2（x +1）2+3的开口向下，对称轴为直线x ＝﹣1，而B （﹣1，b ）直线x ＝﹣1上，C （3，c ）点离直线x ＝﹣1最远，A （﹣2，a ）离直线x ＝﹣1的距离较近，∴c ＜a ＜b ．故选：C ．【点评】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．8．（3分）如图，圆上有两点A ，B ，连接AB ，分别以A ，B 为圆心，AB 的长为半径画弧，两弧相交于点C ，D ，CD 交AB 于点E ，交AB̂于点F ．若EF ＝1，AB ＝6，则该圆的半径长是（ ）A ．4B ．5C ．6D ．10【分析】先根据作图知AB ⊥CD ，再根据垂径定理知AE ＝BE =12AB ＝3，设该圆的半径为r ，根据r 2＝（r ﹣1）2+32求解可得． 【解答】解：由作图知AB ⊥CD 且AB 平分CD ， ∴AE ＝BE =12AB ＝3， 设该圆的半径为r ， 则r 2＝（r ﹣1）2+32，解得：r ＝5，即该圆的半径长是5， 故选：B ．【点评】本题主要考查作图﹣基本作图，解题的关键是熟练掌握线段中垂线的尺规作图和垂径定理及勾股定理等知识点．9．（3分）如图，P 是矩形ABCD 内一点，连结P 与矩形ABCD 各顶点，矩形EFGH 各顶点分别在边AP ，BP ，CP ，DP 上，已知AE ＝2EP ，EF ∥AB ，图中两块阴影部分的面积和为S ．则矩形ABCD 的面积为（ ）A ．4SB ．6SC ．12SD ．18S【分析】根据矩形的性质得到∠DAB ＝∠HEF ＝90°，根据平行线的性质得到∠PEF ＝∠P AB ，求得∠PEH ＝∠P AD ，推出EH ∥AD ，同理，FG ∥BC ，根据相似三角形的性质得到S △PEH S △PAD=（PE PA）2=19，同理，S △PFG S △PBC=19，于是得到结论．【解答】解：∵AE ＝2EP ， ∴PE PA=13，∵四边形ABCD 与四边形EFGH 是矩形， ∴∠DAB ＝∠HEF ＝90°， ∵EF ∥AB ， ∴∠PEF ＝∠P AB ， ∴∠PEH ＝∠P AD ， ∴EH ∥AD ， 同理，FG ∥BC ， ∵EF ∥AB ， ∴△PEF ∽△P AB ， ∴PEPA =PFPB =13，∴S △PEH S △PAD=（PE PA）2=19，同理，S △PFG S △PBC=19，∵S △P AD +S △PBC =12S 矩形ABCD ， ∴S =19（S △P AD +S △PBC ）=19×12S 矩形ABCD， ∴矩形ABCD 的面积＝18S ． 故选：D ．【点评】本题考查了相似三角形的判定和性质，矩形的性质，熟练掌握相似三角形的判定和性质是解题的关键．10．（3分）如图，在坐标系网格中，过点B 的抛物线顶点为A ，且点A ，B ，C ，D ，E ，F ，O 都在格点上，则该抛物线还经过下列选项中的（ ）A ．点CB ．点DC ．点ED ．点F【分析】根据二次函数的性质和图象，可以解答本题． 【解答】解：由图象可得， 该抛物线经过点A 、B 、F ， 故选：D ．【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征，解答本题的关键是明确题意，利用数形结合的思想解答．二、填空题（本题有8个小题，每小题3分，共24分） 11．（3分）已知xy=43，则x−y y =13．【分析】由xy=43，得x =43y ，再代入所求的式子化简即可．【解答】解：x y=43，得x =43y ，把x =43y ，代入x−y y=13．故答案为：13．【点评】考查了比例的性质，找出x 、y 的关系，代入所求式进行约分．12．（3分）将抛物线y ＝x 2+2向上平移1个单位后所得新抛物线的表达式为 y ＝x 2+3 ． 【分析】根据“上加下减，左加右减”的原则进行解答即可．【解答】解：将抛物线y ＝x 2+2向上平移1个单位后所得新抛物线的表达式为y ＝x 2+2+1，即y ＝x 2+3． 故答案是：y ＝x 2+3．【点评】本题考查的是二次函数的图象与几何变换，熟知“上加下减，左加右减”的原则是解答此题的关键．13．（3分）如图，AB ∥CD ∥EF ，点E ，F 分别在线段AD ，BC 上，已知BF ＝4，CF ＝6，AE ＝5，则DE 的长为152．【分析】三条平行线截两条直线，所得的对应线段成比例．依据平行线分线段成比例定理可得结论．【解答】解：∵AB ∥CD ∥EF ， ∴AE DE=BF CF，即5DE=46，∴DE =152， 故答案为：152．【点评】本题主要考查了平行线分线段成比例定理，三条平行线截两条直线，所得的对应线段成比例．14．（3分）如图，在一个半径为3的圆中，若圆周角∠ABC 为30°，则AĈ的长为 π ．【分析】连接OA ，OC ，根据圆周角定理求出∠AOC ，利用弧长公式计算，得到答案． 【解答】解：连接OA ，OC ，由圆周角定理得，∠AOC ＝2∠ABC ＝60°， ∴AC ̂的长=60π×3180=π， 故答案为：π．【点评】本题考查的是弧长的计算，圆周角定理，掌握弧长公式是解题的关键． 15．（3分）如图，AB 是半圆O 的直径，点D ，E 在半圆上，∠DOE ＝100°，点C 在DE ̂上，连接CD ，CE ，则∠DCE 等于 130 度．【分析】补全⊙O ，在⊙O 上AB 的下方取一点M ，连接DM ，EM ．根据圆周角定理，圆内接四边形的性质即可解决问题．【解答】解：补全⊙O，在⊙O上AB的下方取一点M，连接DM，EM．∵∠M=12∠DOE＝50°，∠M+∠DCE＝180°，∴∠DCE＝130°，故答案为130【点评】本题考查圆周角定理，圆内接四边形的性质等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．16．（3分）如图，两个完全相同的正五边形ABCDE，AFGHM的边DE，MH在同一直线上，且有一个公共顶点A，若正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合，则x的最小值为144°．【分析】根据多边形的内角和，可求出∠BAE＝∠AED＝∠F AM＝∠AMH= 180×(5−2)5=108°，即可求出∠EAM的度数，根据旋转的性质，可得x的最小值．【解答】解：∵五边形ABCDE，AFGHM是正五边形∴∠BAE＝∠AED＝∠F AM＝∠AMH=180×(5−2)5=108°，∴∠AEM＝∠AME＝72°，∴∠EAM＝180°﹣72°﹣72°＝36°，∵正五边形ABCDE绕点A旋转x度与正五边形AFGHM重合，顺时针旋转最小需144°，逆时针旋转最小需216°，∴x的最小值为36+108＝144°故答案为：144°【点评】本题考查了旋转的性质，多边形的内角与外角，利用多边形的内角和得出每个内角是解题关键．17．（3分）如图1，G为△ABC纸片的重心，DG∥AC交BC于点D，连结BG，剪去△BGD纸片，剩余部分纸片如图2所示，若原△ABC纸片面积为5，则图2纸片的面积为359．【分析】连接AG，延长AG交BD于E，如图1，设△DGE的面积为S，利用三角形重心的性质得到BE＝CE，AG＝2EG，根据平行线分线段成比例定理得到ED：DC＝EG：AG＝1：2，根据三角形的面积公式得到S△DGC＝2S，最后表示出S△ABC＝18S，即18S＝5，解得S=5 18，然后计算图2纸片的面积．【解答】解：连接AG，延长AG交BD于E，如图1，设△DGE的面积为S，∵G为△ABC纸片的重心，∴BE＝CE，AG＝2EG，∵DG∥AC，∴ED：DC＝EG：AG＝1：2，∴S△DGC＝2S△DEG＝2S，∴S△BEG＝S△CEG＝3S，∴S△ABG＝2S△BEG＝6S，∵S△ABE＝3S+6S＝9S，∴S△ABC＝2S△ABE＝18S，即18S＝5，解得S=5 18，∴S△BDG＝4S=10 9，∴图2纸片的面积＝5−109=359．故答案为359．【点评】本题考查了三角形的重心：三角形的重心是三角形三边中线的交点．重心到顶点的距离与重心到对边中点的距离之比为2：1． 也考查了三角形面积公式．18．（3分）如图，四边形ABDC 内接于半圆O ，AB 为直径，AD 平分∠CAB ，AB ﹣AC ＝4，AD ＝3√7，作DE ⊥AB 于点E ，则BE 的长为 2 ，AC 的长为 5 ．【分析】如图，作DF ⊥AC 交AC 的延长线于F ．由Rt △DFC ≌Rt △DEB （HL ），推出CF ＝BE ，由Rt △ADF ≌Rt △ADE （HL ），推出AF ＝AE ，由AB ﹣AC ＝AE +EB ﹣（AF ﹣CF ）＝2BE ＝4，推出BE ＝2，由△ADE ∽△ABD ，推出AD AB=AE AD，可得AD 2＝AE •AB ，设AE ＝x ，由此构建方程即可解决问题．【解答】解：如图，作DF ⊥AC 交AC 的延长线于F ．∵AD 平分∠CAB ，DF ⊥AC ，DE ⊥AB ， ∴DE ＝DF ， ∵∠DAC ＝∠DAB ， ∴CD ̂=BD ̂， ∴CD ＝DB ，∵∠F ＝∠DEB ＝90°， ∴Rt △DFC ≌Rt △DEB （HL ），∴CF ＝BE ，∵∠F ＝∠AED ＝90°，AD ＝AD ．DF ＝DE ， ∴Rt △ADF ≌Rt △ADE （HL ）， ∴AF ＝AE ，∵AB ﹣AC ＝AE +EB ﹣（AF ﹣CF ）＝2BE ＝4， ∴BE ＝2， ∵AB 是直径， ∴∠ADB ＝90°，∵∠DAE ＝∠BAD ，∠AED ＝∠ADB ＝90°， ∴△ADE ∽△ABD ， ∴AD AB=AE AD，∴AD 2＝AE •AB ，设AE ＝x ， 则有：63＝x （x +2）， 解得x ＝7或﹣9（舍弃）， ∴AE ＝7， ∴AB ＝AE +BE ＝9， ∵AB ﹣AC ＝4， ∴AC ＝5， 故答案为2，5．【点评】本题考查圆周角定理，角平分线的性质定理，全等三角形的判定和性质，勾股定理，相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题．三、解答题（本题有6小题，共46分，解答需写出必要的文字说明、演算步骤或证明过程） 19．（6分）有4张卡片，正面分别写上1，2，3，4，它们的背面都相同．现将它们背面朝上，先从中任意摸出一张，卡片不放回，再任意摸出一张． （1）请用树状图或列表法表示出所有可能的结果． （2）求摸出的两张卡片上的数之和大于5的概率．【分析】（1）首先根据题意画出树状图，得出所有等可能的结果数；（2）根据（1）得出所有等可能的结果数和两张卡片的数字之和大于5的情况数，再利用概率公式求解即可求得答案．【解答】解：（1）根据题意画图如下：共有12种等情况数；（2）根据（1）可得：共有12种等情况数，摸出的两张卡片上的数之和大于5的有4种，则摸出的两张卡片上的数之和大于5的概率是412=1 3．【点评】此题考查的是用列表法或树状图法求概率．注意画树状图法与列表法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件；树状图法适合两步或两步以上完成的事件；注意此题属于不放回实验．20．（6分）如图，△ABC内接于⊙O，请用直尺和圆规按要求作图（保留作图痕迹）．（1）在图1中画出一个圆心角，所作角的度数是∠ACB的2倍．（2）在图2中画出一个圆周角，所作角的度数是∠ACB的2倍．【分析】（1）根据同圆中，同弧所对圆心角等于圆周角的2倍连接OA＝OB即可得；（2）作直线BO，再过点A作BO的垂线，交⊙O于点D，连接CD，则∠ACD即为所求．【解答】解：（1）如图1，∠AOB＝2∠ACB；（2）如图2，∠ACD＝2∠ACB．【点评】本题主要考查作图﹣复杂作图，解题的关键是掌握圆心角、弧、弦的关系及过直线外一点作已知直线的垂线的尺规作图．21．（6分）已知抛物线y＝x2﹣4x+a+1．（1）若抛物线经过点（3，5），求该抛物线的表达式．（2）若该抛物线与x轴有且只有一个交点，求a的值．【分析】（1）利用待定系数法确定函数解析式；（2）利用抛物线与一元二次方程的关系以及根的判别式解答．【解答】解：（1）把（3，5）代入y＝x2﹣4x+a+1，得32﹣4×3+a+1＝5，解得a＝7，故该抛物线解析式是y＝x2﹣4x+8；（2）∵抛物线y＝x2﹣4x+a+1与x轴有且只有一个交点，∴△＝（﹣4）2﹣4（a+1）＝0，解得a＝3．【点评】考查了抛物线与x轴的交点，二次函数图象上点的坐标特征以及待定系数法确定函数解析式，难度不大．22．（8分）如图，在Rt△ABC中，∠B＝90°，BC＞AB，在BC边上取点D，使AB＝BD，构造正方形ABDE，DE交AC于点F，作EG⊥AC交AC于点G，BC于点H．（1）求证：△AEF≌△EDH．（2）若AB＝3，DH＝2DF，求BC的长．【分析】（1）根据ASA证明：△AEF≌△EDH；（2）设DF＝x，则DH＝2x，根据正方形的性质得：AB∥DF，得△DFC∽△BAC，列比例式可得DC的长，可得结论．【解答】证明：（1）∵四边形ABDE是正方形，∴AE ＝DE ，∠AED ＝∠EDH ＝90°，∵EG ⊥AC ，∴∠AGE ＝90°，∴∠GAE +∠AEG ＝∠AEG +∠DEH ＝90°，∴∠GAE ＝∠DEH ，在△AEF 和△EDH 中，∵{∠GAE =∠DEH AE =ED ∠AEF =∠EDH，∴△AEF ≌△EDH （ASA ）；（2）设DF ＝x ，则DH ＝2x ，∵△AEF ≌△EDH ．∴EF ＝DH ＝2x ，∴ED ＝EF +DF ＝3x ＝AB ，∵四边形ABDE 是正方形，∴AB ∥DF ，∴△DFC ∽△BAC ，∴DF AB =DC BC =x 3x ，∵BD ＝3，∴DC =32，∴BC ＝BD +CD ＝3+32=4.5．【点评】本题考查了三角形全等的性质和判定、正方形的性质、三角形相似的判定和性质等知识，熟练掌握三角形全等的判定是关键．23．（8分）小张准备给长方形客厅铺设瓷砖，已知客厅长AB ＝8m ，宽BC ＝6m ，现将其划分成一个长方形EFGH 区域I 和环形区域Ⅱ，区域Ⅰ用甲、乙瓷砖铺设，其中甲瓷砖铺设成的是两个全等的菱形图案，区域Ⅱ用丙瓷砖铺设，如图所示，已知N 是GH 中点，点M 在边HE 上，HN ＝3HM ，设HM ＝x （m ）．（1）用含x 的代数式表示以下数量．铺设甲瓷砖的面积为 12x 2 m 2．铺设丙瓷砖的面积为 48﹣24x 2 m 2．（2）若甲、乙、丙瓷砖单价分别为300元/m2，200元/m2，100元/m2，且EF≥FG+2，铺设好整个客厅，三种瓷砖总价至少需要多少钱？【分析】（1）由HM＝x（m）得出HN＝3x（m），则EF＝GH＝6x（m），再根据菱形的面积、三角形的面积、矩形的面积计算方法即可得出结果；（2）由已知条件EF≥FG+2，得出x≥1，求出三种瓷砖总价，即可得出结果．【解答】解：（1）设HM＝x（m），则HN＝3x（m），根据题意得：EF＝GH＝6x（m），FG＝4x（m），∴铺设甲瓷砖的面积为2×12×6x×2x＝12x2（m2），铺设乙瓷砖的面积为8×12×3x×x＝12x2（m2），∴铺设丙瓷砖的面积为8×6﹣12x2﹣12x2＝48﹣24x2（m2）；故答案为12x2，48﹣24x2；（2）∵EF≥FG+2，∴6x≥4x+2，解得：x≥1，∴铺设好整个客厅，三种瓷砖总价为300×12x2+200×12x2+100（48﹣24x2）＝3600x2+4800≥3600+4800＝8400（元），即铺设好整个客厅，三种瓷砖总价至少需要8400元．【点评】本题考查了菱形、矩形的性质，菱形、矩形和三角形面积的计算以及列代数式；熟练掌握菱形和矩形的性质，列出各种瓷砖的面积是解题关键．24．（12分）如图，在矩形BCD中，AB＝3，AD＝8，O为AD中点，P是线段AO上一动点，以O为圆心，OP为半径作⊙O分别交BO及BO延长线于点E，F，延长AE交BC 于点H．（1）当OP＝2时，求BH的长．（2）当AH 交⊙O 于另一点G 时，连接FG ，DF ，作DM ⊥BF 于点M ，求证：△EFG ∽△FDM ．（3）连结HO ，当△EHO 是直角三角形时，求OP 的长．【分析】（1）在Rt △ABO 中，利用勾股定理求出OB ，由BH ∥OA ，推出BH OA =BE EO ，由此即可解决问题；（2）利用两角对应相等两三角形相似即可证明；（3）分两种情形画出图形分别求解即可；【解答】解：（1）如图1中，∵四边形ABCD 是矩形，∴∠BAD ＝90°，AD ∥BC ，∵AB ＝3，AO ＝OD ＝4，∴OB =√32+42=5，∵OP ＝OE ＝2，∴BE ＝3，∵BH ∥OA ，∴BH OA =BE EO ， ∴BH 4=32，∴BH ＝6．（2）如图2中，∵EF 是直径，∴∠EGF ＝90°，∵OA ＝OD ，∠AOE ＝∠DOF ，OE ＝OF ，∴△AOE ≌△DOF （SAS ），∴∠EAO ＝∠ODF ，∴AH ∥DF ，∴∠DFG ＝∠EGF ＝90°，∵DM ⊥BF ，∴∠DMF ＝∠EGF ＝90°，∵∠GFE +∠DFM ＝90°，∠DFM +∠FDM ＝90°，∴∠EFG ＝∠FDM ，∴△EFG ∽△FDM ．（3）如图3﹣1中，当∠HEO ＝90°时，∵12•AB •AO =12•OB •AE ，∴AE =125， ∴OE =2−AE 2=165， ∴OP ＝OE =165．如图3﹣2中，当∠EOH ＝90°时，∵BC ∥AD ，∴∠BOA ＝∠OBH ，∵∠BAO ＝∠BOH ＝90°，∴△ABO ∽△OHB ，∴OB BH =OA OB ， ∴5BH=45，∴BH =254， ∵OA ∥BH ， ∴OE EB =OA BH =4254=1625，∴OE =1641•OB =8041，∴OP ＝OE =8041，综上所述，OP 的值为165或8041．【点评】本题属于圆综合题，考查了矩形的性质，圆周角定理，全等三角形的判定和性质，相似三角形的判定和性质，平行线分线段成比例定理等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考压轴题．。

浙江省温州市瑞安市五校联考九年级（上）期末数学试卷一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．（4分）若＝，则的值等于（）A．B．C．D．2．（4分）⊙O的半径为4cm，若点P到圆心的距离为3cm，点P在（）A．圆内B．圆上C．圆外D．无法确定3．（4分）二次函数y＝x2﹣1的图象与y轴的交点坐标是（）A．（0，1）B．（1，0）C．（﹣1，0）D．（0，﹣1）4．（4分）若两个三角形的相似比为1：2，则它们的面积比为（）A．1：2B．1：4C．2：1D．4：15．（4分）一个不透明的盒子里有n个除颜色外其他完全相同的小球，其中有9个黄球．每次摸球前先将盒子里的球摇匀，任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么估计盒子中小球的个数n为（）A．20B．24C．28D．306．（4分）已知二次函数的图象（0≤x≤4）如图，关于该函数在所给自变量的取值范围内，下列说法正确的是（）A．有最大值2，有最小值﹣2.5B．有最大值2，有最小值1.5C．有最大值1.5，有最小值﹣2.5D．有最大值2，无最小值．7．（4分）如图，D是等边△ABC外接圆上的点，且∠DAC＝20°，则∠ACD的度数为（）A．20°B．30°C．40°D．45°8．（4分）如图，有一块直角三角形余料ABC，∠BAC＝90°，D是AC的中点，现从中切出一条矩形纸条DEFG，其中E，F在BC上，点G在AB上，若BF＝4.5cm，CE＝2cm，则纸条GD的长为（）A．3 cm B．2cm C．cm D．cm9．（4分）二次函数y1＝x2+bx+c与一次函数y2＝kx﹣9的图象交于点A（2，5）和点B（3，m），要使y1＜y2，则x的取值范围是（）A．2＜x＜3B．x＞2C．x＜3D．x＜2或x＞3 10．（4分）如图，点A，B，C均在坐标轴上，AO＝BO＝CO＝1，过A，O，C作⊙D，E 是⊙D上任意一点，连结CE，BE，则CE2+BE2的最大值是（）A．4B．5C．6D．4+二、填空题（本题有6小题.每小题5分，共30分）11．（5分）某校九年1班共有45位学生，其中男生有25人，现从中任选一位学生，选中女生的概率是．12．（5分）已知扇形的圆心角为120°，弧长为6π，则它的半径为．13．（5分）如图，点B，E分别在线段AC，DF上，若AD∥BE∥CF，AB＝3，BC＝2，DE ＝4.5，则DF的长为．14．（5分）若二次函数y＝ax2+2ax﹣3的图象与x轴的一个交点是（2，0），则与x轴的另一个交点坐标是．15．（5分）如图，△ABC内接于⊙O，AD⊥BC于点D，AD＝BD．若⊙O的半径OB＝2，则AC的长为．16．（5分）两幢大楼的部分截面及相关数据如图，小明在甲楼A处透过窗户E发现乙楼F 处出现火灾，此时A，E，F在同一直线上．跑到一楼时，消防员正在进行喷水灭火，水流路线呈抛物线，在1.2m高的D处喷出，水流正好经过E，F．若点B和点E、点C和F的离地高度分别相同，现消防员将水流抛物线向上平移0.4m，再向左后退了m，恰好把水喷到F处进行灭火．三、解答题（本题有8小题，共80分）17．（6分）如图，在⊙O中，AB＝CD．求证：AD＝BC．18．（8分）一个不透明的袋子中装有红、白两种颜色的小球，这些球除颜色外都相同，其中红球有2个，若从中随机摸出一个球，这个球是白球的概率为．（1）求袋子中白球的个数；（请通过列式或列方程解答）（2）随机摸出一个球后，放回并搅匀，再随机摸出一个球，求两次都摸到相同颜色的小球的概率．（请结合树状图或列表解答）19．（10分）如图，点O是线段AB的中点，根据要求完成下题：（1）在图中补画完成：第一步，以AB为直径的画出⊙O；第二步，以B为圆心，以BO为半径画圆弧，交⊙O于点C，连接点CA，CO；（2）设AB＝6，求扇形AOC的面积．（结果保留π）20．（10分）如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的C'处，点D落在点D'处，C'D'交线段AE于点M．（1）求证：△BC'F∽△AMC'；（2）若C'是AB的中点，AB＝6，BC＝9，求AM的长．21．（10分）如图，二次函数的图象的顶点坐标为（1，），现将等腰直角三角板直角顶点放在原点O，一个锐角顶点A在此二次函数的图象上，而另一个锐角顶点B在第二象限，且点A的坐标为（2，1）．（1）求该二次函数的表达式；（2）判断点B是否在此二次函数的图象上，并说明理由．22．（10分）甲乙两位同学利用灯光下的影子来测量一路灯A的高度，如图，当甲走到点C处时，乙测得甲直立身高CD与其影子长CE正好相等，接着甲沿BC方向继续向前走，走到点E处时，甲直立身高EF的影子恰好是线段EG，并测得EG＝2.5m．已知甲直立时的身高为1.75m，求路灯的高AB的长．（结果精确到0.1m）23．（12分）如图，二次函数y＝﹣x2+x+2的图象与x轴交于点A，B，与y轴交于点C．点P是该函数图象上的动点，且位于第一象限，设点P的横坐标为x．（1）写出线段AC，BC的长度：AC＝，BC＝；（2）记△BCP的面积为S，求S关于x的函数表达式；（3）过点P作PH⊥BC，垂足为H，连结AH，AP，设AP与BC交于点K，探究：是否存在四边形ACPH为平行四边形？若存在，请求出的值；若不存在，请说明理由，并求出的最大值．24．（14分）如图，AB是⊙O的直径，＝，连结AC，过点C作直线l∥AB，点P是直线l上的一个动点，直线P A与⊙O交于另一点D，连结CD，设直线PB与直线AC交于点E．（1）求∠BAC的度数；（2）当点D在AB上方，且CD⊥BP时，求证：PC＝AC；（3）在点P的运动过程中①当点A在线段PB的中垂线上或点B在线段P A的中垂线上时，求出所有满足条件的∠ACD的度数；②设⊙O的半径为6，点E到直线l的距离为3，连结BD，DE，直接写出△BDE的面积．浙江省温州市瑞安市五校联考九年级（上）期末数学试卷参考答案一、选择题（本题有10小题，每小题4分，共40分．每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．C；2．A；3．D；4．B；5．D；6．A；7．C；8．C；9．A；10．C；二、填空题（本题有6小题.每小题5分，共30分）11．；12．9；13．7.5；14．（﹣4，0）；15．2；16．﹣10；三、解答题（本题有8小题，共80分）17．；18．；19．；20．；21．；22．；23．；2；24．；。

2019-2020学年九年级（上）期末数学试卷一、选择题1．抛物线y＝x2+2x+3与y轴的交点为（）A．（0，2）B．（2，0）C．（0，3）D．（3，0）2．如图，是一个纸折的小风车模型，将它绕着旋转中心旋转下列哪个度数后不能与原图形重合（）A．90°B．135°C．180°D．270°3．已知一个扇形的半径为3，弧长为2π，那么它所对的圆心角度数为（）A．240°B．120°C．90°D．60°4．若将函数y＝2x2的图象向右平行移动1个单位，再向上平移3个单位，得到的抛物线是（）A．y＝2（x+5）2﹣1 B．y＝2（x+5）2+1C．y＝2（x﹣1）2+3 D．y＝2（x+1）2﹣35．如图A是某公园的进口，B，C，D是三个不同的出口，小明从A处进入公园，那么从B，C，D三个出口中恰好在C出口出来的概率为（）A．B．C．D．6．已知点A（﹣2，a），B（2，b），C（4，c）是抛物线y＝x2﹣4x上的三点，则a，b，c 的大小关系为（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞c＞b7．如图，下面图形及各个选项均是由边长为1的小方格组成的网格，三角形的顶点均在小方格的顶点上，下列四个选项中哪一个阴影部分的三角形与已知△ABC相似（）A．B．C．D．8．“双11”前，小明的妈妈花了120元钱在淘宝上购买了一批室内拖鞋，在“双11”大减价期间她发现回款的拖鞋单价每双降了5元，于是又花了100元钱购买了一批回款室内拖鞋，且比上次还多了2双．若设拖鞋原价每双为x元，则可以列出方程为（）A．B．C．D．9．反比例函数y＝，y＝图象如图所示，点A在y＝图象上，连接OA交y＝图象于点B，则AB：BO的比为（）A．1：2 B．2：3 C．4：5 D．4：910．如图矩形ABCD中，E是CD延长线上一点，连结BE交AD于点F，连结CF，已知AB＝1，BC＝2，若△ABF与△CEF的面积相等，则DE的长为（）A．1 B．C．D．二、填空题（本题有6小题，每小题5分，共30分）11．某灯具厂从一批LED灯泡中随机抽取100个进行质量检测，结果有99个灯泡质量合格，那么可以估计这批灯泡的合格率约为．12．已知两个相似三角形△ABC与△DEF的相似比为3．则△ABC与△DEF的面积之比为．13．一个小球从水平面开始竖直向上发射，小球的高度h（m）关于运动时间t（s）的函数表达式为h＝at2+bt，其图象如图所示．若小球在发射后第2s与第6s时的高度相等，则小球从发射到回到水平面共需时间（s）．14．某公路上有一隧道，顶部是圆弧形拱顶，圆心为O，隧道的水平宽AB为24m，AB离地面的高度AE＝10 m，拱顶最高处C离地面的高度CD为18m，在拱顶的M，N处安装照明灯，且M，N离地面的高度相等都等于17m，则MN＝m．15．已知 Rt△ACB中，∠ACB＝90°，AB﹣BC＝2，AC＝4，以三边分别向外作三个正方形，连接DE，FG，HI，得到六边形DEFGHI，则六边形DEFGHI的面积为．16．如图，以AD为直径作⊙O，点B为半圆弧的中点，连接AB，以如图所示的AD，AB为邻边作平行四边形ABCD，连结AC交⊙O于点E，连结BE并延长交CD于F．若AD＝6，则DF＝．三、解答题（本题有8小题，共80分）17．（1）计算：+（π﹣2019）0﹣（+1）2（2）解方程：18．如图所示平行四边形ABCD中，EF分别是边AD，BC上的点，且AE＝CF．（1）求证：BE＝DF；（2）连结AF，若AD＝DF，∠ADF＝40°，求∠AFB的度数．19．在甲口袋中有三个球分别标有数码1，﹣2，3；在乙口袋中也有三个球分别标有数码4，﹣5，6；已知口袋均不透明，六个球除标码不同外其他均相同，小明从甲口袋中任取一个球，并记下数码，小林从乙口袋中任取一个球，并记下数码．（1）用树状图或列表法表示所有可能的结果；（2）求所抽取的两个球数码的乘积为负数的概率．20．如图Rt△ABC与 Rt△DEF中，∠A＝∠D＝90°，∠B＝40°，∠E＝20°，用一条过顶点的线段将 Rt△ABC分割成两个三角形，再用另一条过顶点的线段将 Rt△DEF也分割成两个三角形；所分割成的四个三角形恰好是两对相似三角形．（要求：1．用三种不同的方法；2．在图中标出相应的锐角度数．）21．如图，Rt△ABC中，∠C＝90°，在BC上取一点D使AD＝BD，连结AD，作△ACD的外接圆⊙O，交AB于点E．（1）求证：AE＝BE；（2）若CD＝3，AB＝4，求AC的长．22．如图直角坐标系中，△ABO，O为坐标原点，A（0，3），B（6，3），二次函数y＝﹣x2+bx+c的图象经过点A，B，点P为抛物线上AB上方的一个点，连结PA，作PQ⊥AB垂足为H，交OB于点Q．（1）求b，c的值；（2）当∠APQ＝∠B时，求点P的坐标；（3）当△APH面积是四边形AOQH面积的2倍时，求点P的坐标．23．如图一个五边形的空地ABCDE，AB∥CD，BC∥DE，∠C＝90°，已知AB＝4（m），BC ＝10（m），CD＝14（m），DE＝5（m），准备在五边形中设计一个矩形的休闲亭MNPQ，剩下部分设计绿植．设计要求NP∥CD，PQ∥BC，矩形MNPQ到五边形ABCDE三边AB，BC，CD的距离相等，都等于x（m），延长QM交AE与H，MH＝1（m）．（1）五边形ABCDE的面积为（m2）；（2）设矩形MNPQ的面积为y（m2），求y关于x的函数关系式；（3）若矩形MNPQ休闲亭的造价为每平方米0.5万元，剩下部分绿植的造价为每平方米0.1万元，求总造价的最大值．24．如图 Rt△ABC中，∠ABC＝90°，P是斜边AC上一个动点，以BP为直径作⊙O交BC 于点D，与AC的另一个交点E，连接DE．（1）当时，①若＝130°，求∠C的度数；②求证AB＝AP；（2）当AB＝15，BC＝20时①是否存在点P，使得△BDE是等腰三角形，若存在，求出所有符合条件的CP的长；②以D为端点过P作射线DH，作点O关于DE的对称点Q恰好落在∠CPH内，则CP的取值范围为．（直接写出结果）参考答案一、选择题（本题有10小题，每小题4分，共40分每小题只有一个选项是正确的，不选、多选、错选，均不给分）1．抛物线y＝x2+2x+3与y轴的交点为（）A．（0，2）B．（2，0）C．（0，3）D．（3，0）解：把x＝0代入y＝x2+2x+3，求得y＝3，∴抛物线y＝x2+2x+3，与y轴的交点坐标为（0，3）．故选：C．2．如图，是一个纸折的小风车模型，将它绕着旋转中心旋转下列哪个度数后不能与原图形重合（）A．90°B．135°C．180°D．270°解：图案可以被平分成四部分，因而每部分被分成的圆心角是90°，并且圆具有旋转不变性，因而旋转90度的整数倍，就可以与自身重合，故选：B．3．已知一个扇形的半径为3，弧长为2π，那么它所对的圆心角度数为（）A．240°B．120°C．90°D．60°解：设扇形的圆心角为n°，∵扇形的半径为3，弧长为2π，∴2π＝，解得：n＝120，即圆心角是120°，故选：B．4．若将函数y＝2x2的图象向右平行移动1个单位，再向上平移3个单位，得到的抛物线是（）A．y＝2（x+5）2﹣1 B．y＝2（x+5）2+1C．y＝2（x﹣1）2+3 D．y＝2（x+1）2﹣3解：函数y＝2x2的图象向右平行移动1个单位，再向上平移3个单位，得到y＝2（x﹣1）2+3．故选：C．5．如图A是某公园的进口，B，C，D是三个不同的出口，小明从A处进入公园，那么从B，C，D三个出口中恰好在C出口出来的概率为（）A．B．C．D．解：∵小明从A处进入公园，那么从B，C，D三个出口出来共有3种等可能结果，其中从C出口出来是其中一种结果，∴恰好在C出口出来的概率为，故选：B．6．已知点A（﹣2，a），B（2，b），C（4，c）是抛物线y＝x2﹣4x上的三点，则a，b，c 的大小关系为（）A．b＞c＞a B．b＞a＞c C．c＞a＞b D．a＞c＞b解：∵抛物线y＝x2﹣4x＝（x﹣2）2﹣4，∴该抛物线的对称轴是直线x＝2，当x＞2时，y随x的增大而增大，当x＜2时，y随x 的增大而减小，∵点A（﹣2，a），B（2，b），C（4，c）是抛物线y＝x2﹣4x的三点，∵2﹣（﹣2）＝4，2﹣2＝0，4﹣2＝2，∴a＞c＞b，故选：D．7．如图，下面图形及各个选项均是由边长为1的小方格组成的网格，三角形的顶点均在小方格的顶点上，下列四个选项中哪一个阴影部分的三角形与已知△ABC相似（）A．B．C．D．解：根据题意得：AC＝＝，AB＝＝，BC＝1，∴BC：AB：AC＝1：：，A、三边之比为1：：，选项A符合题意；B、三边之比：：3，选项B不符合题意；C、三边之比为2：：，选项C不符合题意；D、三边之比为：：4，选项D不符合题意．故选：A．8．“双11”前，小明的妈妈花了120元钱在淘宝上购买了一批室内拖鞋，在“双11”大减价期间她发现回款的拖鞋单价每双降了5元，于是又花了100元钱购买了一批回款室内拖鞋，且比上次还多了2双．若设拖鞋原价每双为x元，则可以列出方程为（）A．B．C．D．解：设拖鞋原价每双为x元，则“双11”大减价期间该款拖鞋价格每双为（x﹣5）元，依题意，得：＝﹣2．故选：D．9．反比例函数y＝，y＝图象如图所示，点A在y＝图象上，连接OA交y＝图象于点B，则AB：BO的比为（）A．1：2 B．2：3 C．4：5 D．4：9解：作AM⊥x轴于M，BN⊥x轴于N，∵点A在y＝图象上，连接OA交y＝图象于点B，∴S△AOM＝×9＝，S△BOC＝＝2，∵AM∥BN，∴＝（）2＝，∴＝，∴＝，即＝，故选：A．10．如图矩形ABCD中，E是CD延长线上一点，连结BE交AD于点F，连结CF，已知AB＝1，BC＝2，若△ABF与△CEF的面积相等，则DE的长为（）A．1 B．C．D．解：设DE＝x．∵DF∥BC，∴△EFD∽△EBC，∴＝，∴＝，∴DF＝，AF＝2﹣＝，∵△ABF与△CEF的面积相等，∴•AF•AB＝•EC•DF，∴×1＝×x+1，∴解得x＝或（舍弃），故选：D．二、填空题（本题有6小题，每小题5分，共30分）11．某灯具厂从一批LED灯泡中随机抽取100个进行质量检测，结果有99个灯泡质量合格，那么可以估计这批灯泡的合格率约为99% ．解：这批LED灯泡的合格率＝99÷100×100%＝99%．故答案为：99%．12．已知两个相似三角形△ABC与△DEF的相似比为3．则△ABC与△DEF的面积之比为9 ．解：∵△ABC与△DEF的相似比为3，∴△ABC与△DEF的面积之比为9．故答案为9．13．一个小球从水平面开始竖直向上发射，小球的高度h（m）关于运动时间t（s）的函数表达式为h＝at2+bt，其图象如图所示．若小球在发射后第2s与第6s时的高度相等，则小球从发射到回到水平面共需时间8 （s）．解：由题意可知：小球在发射后第2s与第6s时的高度相等，则函数h＝at2+bt的对称轴t＝＝4，故小球从发射到回到水平面共需时间8秒，故答案是：8．14．某公路上有一隧道，顶部是圆弧形拱顶，圆心为O，隧道的水平宽AB为24m，AB离地面的高度AE＝10 m，拱顶最高处C离地面的高度CD为18m，在拱顶的M，N处安装照明灯，且M，N离地面的高度相等都等于17m，则MN＝10 m．解：设CD于AB交于G，与MN交于H，∵CD＝18m，AE＝10m，AB＝24m，HD＝17m，∴CG＝8m，AG＝12m，CH＝1m，设圆拱的半径为r，在Rt△AOG中，OA2＝OG2+AG2，∴r2＝（r﹣8）+122，解得r＝13，∴OC＝13m，∴OH＝13﹣1＝12m，在Rt△MOH中，OM2＝OH2+MH2，∴132＝122+MH2，解得MH2＝25，∴MH＝5m，∴MN＝10m，故答案为10．15．已知 Rt△ACB中，∠ACB＝90°，AB﹣BC＝2，AC＝4，以三边分别向外作三个正方形，连接DE，FG，HI，得到六边形DEFGHI，则六边形DEFGHI的面积为74 ．解：如图，作DJ⊥EA交EA的延长线于J．∵∠DAC＝∠JAB＝90°，∴∠DAJ＝∠CAB，∵AD＝AB，∠J＝∠ACB＝90，∴△ADJ≌△ABC（AAS），∴DJ＝BC，∵S△ABD＝•AE•DJ，S△ABC＝•AC•BC，AE＝AB，∴S△AED＝S△ABC，同理可证S△ABC＝S△BFG，∵AB﹣BC＝2，AC＝4，∴可以假设BC＝x，则AB＝x+2，∴（x+2）2＝x2+42解得x＝3，∴AC＝4，BC＝3，AB＝5，∴六边形DEFGHI的面积＝4××3×4+4×4+3×3+5×5＝74，故答案为74．16．如图，以AD为直径作⊙O，点B为半圆弧的中点，连接AB，以如图所示的AD，AB 为邻边作平行四边形ABCD，连结AC交⊙O于点E，连结BE并延长交CD于F．若AD＝6，则DF＝．解：如图，连接BD交AC于O，连接DE，作FM⊥AC于M，FN⊥DE于N．∵＝，∴AB＝BD，∵AD是直径，∴∠ABD＝∠AED＝90°，∴∠BAD＝∠BDA＝∠AEB＝45°，∵∠AEB＝∠CEF＝45°，∠CED＝90°，∴∠FED＝∠FEC＝45°，∵FM⊥EC．FN⊥ED，∴FM＝FN，∴＝＝＝，∵四边形ABCD是平行四边形，∴OB＝OD，AB∥CD，∴∠BAO＝∠DCE，∴tan∠DCE＝tan∠ABO＝＝＝，∴DF：CF＝DE+CE＝1：2，∴AD＝6，△ABD是等腰直角三角形，∴AB＝BD＝CD＝3，∴DF＝CD＝故答案为．三、解答题（本题有8小题，共80分）17．（1）计算：+（π﹣2019）0﹣（+1）2（2）解方程：解：（1）原式＝2+1﹣（3+2+1）＝2+1﹣4﹣2＝﹣3；（2）去分母得3（x﹣1）＝2（2x+3），去括号得3x﹣3＝4x+6，移项得3x﹣4x＝9，合并的得﹣x＝9，系数化为1得x＝﹣9．18．如图所示平行四边形ABCD中，EF分别是边AD，BC上的点，且AE＝CF．（1）求证：BE＝DF；（2）连结AF，若AD＝DF，∠ADF＝40°，求∠AFB的度数．【解答】（1）证明：在平行四边形ABCD中，AD∥BC，AD＝BC，∵AE＝CF，∴DE∥BF，DE＝BF∴四边形BEDF是平行四边形∴BE＝DF．（2）∵AD＝DF，∠ADF＝40°∴∠DAF＝∠AFD＝70°∵AD∥BC∴∠AFB＝∠FAD＝70°．19．在甲口袋中有三个球分别标有数码1，﹣2，3；在乙口袋中也有三个球分别标有数码4，﹣5，6；已知口袋均不透明，六个球除标码不同外其他均相同，小明从甲口袋中任取一个球，并记下数码，小林从乙口袋中任取一个球，并记下数码．（1）用树状图或列表法表示所有可能的结果；（2）求所抽取的两个球数码的乘积为负数的概率．解：（1）列表如下：（2）由表可知，共有9种等可能结果，其中所抽取的两个球数码的乘积为负数的由4种结果，∴所抽取的两个球数码的乘积为负数的概率为．20．如图Rt△ABC与 Rt△DEF中，∠A＝∠D＝90°，∠B＝40°，∠E＝20°，用一条过顶点的线段将 Rt△ABC分割成两个三角形，再用另一条过顶点的线段将 Rt△DEF也分割成两个三角形；所分割成的四个三角形恰好是两对相似三角形．（要求：1．用三种不同的方法；2．在图中标出相应的锐角度数．）解：方法一：方法二：方法三：方法四：方法五：21．如图，Rt△ABC中，∠C＝90°，在BC上取一点D使AD＝BD，连结AD，作△ACD的外接圆⊙O，交AB于点E．（1）求证：AE＝BE；（2）若CD＝3，AB＝4，求AC的长．解：（1）证明：连结DE，∵∠C＝90°，∴AD为直径，∴DE⊥AB，∵AD＝BD，∴AE＝BE；（2）设BD＝x，∵∠B＝∠B，∠C＝∠DEB＝90°∴△ABC～△DBE，∴，∴，∴x＝5．∴AD＝BD＝5，∴AC＝＝4．22．如图直角坐标系中，△ABO，O为坐标原点，A（0，3），B（6，3），二次函数y＝﹣x2+bx+c的图象经过点A，B，点P为抛物线上AB上方的一个点，连结PA，作PQ⊥AB垂足为H，交OB于点Q．（1）求b，c的值；（2）当∠APQ＝∠B时，求点P的坐标；（3）当△APH面积是四边形AOQH面积的2倍时，求点P的坐标．解：（1）把A（0，3），B（6，3）代入y＝﹣x2+bx+c并解得：；（2）设P（m，﹣m2+6m+3）∵∠P＝∠B，∠AHP＝∠OAB＝90°，∴△ABO～△HPA，∴，∴，解得m＝4．∴P（4，11）（3）当△APH的面积是四边形AOQH的面积的2倍时，则2（AO+HQ）＝PH∴，得：m1＝4，m2＝3，∴P（4，11）或P（3，12）23．如图一个五边形的空地ABCDE，AB∥CD，BC∥DE，∠C＝90°，已知AB＝4（m），BC ＝10（m），CD＝14（m），DE＝5（m），准备在五边形中设计一个矩形的休闲亭MNPQ，剩下部分设计绿植．设计要求NP∥CD，PQ∥BC，矩形MNPQ到五边形ABCDE三边AB，BC，CD的距离相等，都等于x（m），延长QM交AE与H，MH＝1（m）．（1）五边形ABCDE的面积为115 （m2）；（2）设矩形MNPQ的面积为y（m2），求y关于x的函数关系式；（3）若矩形MNPQ休闲亭的造价为每平方米0.5万元，剩下部分绿植的造价为每平方米0.1万元，求总造价的最大值．解：（1）五边形ABCDE的面积为＝5×14+（4+14）（10﹣5）＝70+45＝115（m2）；故答案为：115；（2）由题意可以得：PQ＝（10﹣2x），MQ＝（3+x），∴y＝（10﹣2x）（x+3）＝﹣2x2+4x+30，（3）设总造价为w（万元），由题意得，w＝115×0.1+0.4（﹣2x2+4x+30）w＝﹣0.8x2+1.6x+23.5，当x＝1时，w最大值＝24.3，答：总造价的最大值为24.3万元．24．如图 Rt△ABC中，∠ABC＝90°，P是斜边AC上一个动点，以BP为直径作⊙O交BC 于点D，与AC的另一个交点E，连接DE．（1）当时，①若＝130°，求∠C的度数；②求证AB＝AP；（2）当AB＝15，BC＝20时①是否存在点P，使得△BDE是等腰三角形，若存在，求出所有符合条件的CP的长；②以D为端点过P作射线DH，作点O关于DE的对称点Q恰好落在∠CPH内，则CP的取值范围为7＜CP＜12.5 ．（直接写出结果）【解答】（1）①解：连接BE，如图1所示：∵BP是直径，∴∠BEC＝90°，∵＝130°，∴＝50°，∵＝，∴＝100°，∴∠CBE＝50°，∴∠C＝40°；②证明：∵＝，∴∠CBP＝∠EBP，∵∠ABE+∠A＝90°，∠C+∠A＝90°，∴∠C＝∠ABE，∵∠APB＝∠CBP+∠C，∠ABP＝∠EBP+∠ABE，∴∠APB＝∠ABP，∴AP＝AB；（2）解：①由AB＝15，BC＝20，由勾股定理得：AC＝＝＝25，∵AB•BC＝AC•BE，即×15×20＝×25×BE∴BE＝12，连接DP，如图1﹣1所示：∵BP是直径，∴∠PDB＝90°，∵∠ABC＝90°，∴PD∥AB，∴△DCP∽△BCA，∴＝，∴CP＝＝＝CD，△BDE是等腰三角形，分三种情况：当BD＝BE时，BD＝BE＝12，∴CD＝BC﹣BD＝20﹣12＝8，∴CP＝CD＝×8＝10；当BD＝ED时，可知点D是Rt△CBE斜边的中线，∴CD＝BC＝10，∴CP＝CD＝×10＝；当DE＝BE时，作EH⊥BC，则H是BD中点，EH∥AB，如图1﹣2所示：AE＝＝＝9，∴CE＝AC﹣AE＝25﹣9＝16，CH＝BC﹣BH＝20﹣BH，∵EH∥AB，∴＝，即＝，解得：BH＝，∴BD＝2BH＝，∴CD＝BC﹣BD＝20﹣＝，∴CP＝CD＝×＝7；综上所述，△BDE是等腰三角形，符合条件的CP的长为10或或7；②当点Q落在∠CPH的边PH上时，CP最小，如图2所示：连接OD、OQ、OE、QE、BE，由对称的性质得：DE垂直平分OQ，∴OD＝QD，OE＝QE，∵OD＝OE，∴OD＝OE＝QD＝QE，∴四边形ODQE是菱形，∴PQ∥OE，∵PB为直径，∴∠PDB＝90°，∴PD⊥BC，∵∠ABC＝90°，∴AB⊥BC，∴PD∥AB，∴DE∥AB，∵OB＝OP，∴OE为△ABP中位线，∴PE＝AE＝9，∴PC＝AC﹣PE﹣AE＝25﹣9﹣9＝7；当点Q落在∠CPH的边PC上时，CP最大，如图3所示：连接OD、OQ、OE、QD，同理得：四边形ODQE是菱形，∴OD∥QE，连接DF，∵∠DBC＝90°，∴DF是直径，∴D、O、F三点共线，∴DF∥AQ，∴∠OFB＝∠A，∵OB＝OF，∴∠OFB＝∠OBF＝∠A，∴PA＝PB，∵∠OBF+∠CBP＝∠A+∠C＝90°，∴∠CBP＝∠C，∴PB＝PC＝PA，∴PC＝AC＝12.5，∴7＜CP＜12.5，故答案为：7＜CP＜12.5．。

浙江省温州市瑞安市集云实验学校等五校2019--2020学年九年级上学期期末联考科学试题学校:___________姓名：___________班级：___________考号：___________一、选择题1．在下列生活和生产中，发生了化学变化的是A．煤气燃烧B．开水沸腾C．雪糕熔化D．雕刻印章2．下图是生活中常见的水果的pH值。

其中碱性最强的水果是A．乌梅B．葡萄C．香蕉D．西瓜3．某宠物饮水机，铭牌上标有“3W”字样。

“3W”表示饮水机的（）A．额定电压B．额定电功C．额定电流D．额定功率4．生病除了药物治疗外，食疗和生活习惯也很重要。

医生对一位患者提出的健康建议是胡萝卜猪肝正对口，夜间出门结伴走。

据此推知这位患者可能患的是A．贫血症B．脚气病C．夜盲症D．佝偻病5．铱-192具有放射性，其裂变发出的物质能穿透三十多毫米厚的钢板，这一性质可用于金属内部探伤。

结合图示可推知，铱-192发出的用于金属内部探伤的最有可能的是A．可见光B．α射线C．β射线D．γ射线6．如图所示为小明学习“人体内的物质运输”后整理的部分笔记，他的标注正确的是A．标注①B．标注②C．标注③D．标注④7．用下列方法匀速提升同一重物，若不计绳子、滑轮的重力及摩擦，其中最省力的是A．B．C．D．8．自行车是简单机械的巧妙结合，如踏脚用到了杠杆原理。

若作用在脚踏板上的力为F，下列图中能正确表示出该力的力臂的是A．B．C．D．9．食醋里通常含有3%～5%的醋酸(CH3COOH)，食醋与鸡蛋壳反应产生能使澄清石灰水变浑浊的气体。

下列能作为醋酸属于酸的证据的是( )A．产生的气体是二氧化碳B．醋酸在水溶液里电离出的阳离子全部是H＋C．加水稀释食醋，溶液pH变大D．不宜用铝制容器盛装食醋10．图为“探究焦耳定律”的实验示意图。

用该实验装置在“研究电流做功产生的热量与电阻的关系”实验时，需要甲、乙两装置中相等的量是A．电阻和电流B．电流和通电时间C．电阻和通电时间D．电压、电流和通电时间11．科学家发明了一种车用制氢装置，其制氢气的原理是：硼（B）和水在高温下反应生成氢氧化硼和氢气．反应的化学方程式为：2B+6H2O 高温2B（OH）3+3H2 ，该反应属于（）A．置换反应B．分解反应C．化合反应D．复分解反应12．某智能百叶窗的叶片上贴有太阳能板，在光照时发电，给电动机供电以调节百叶窗的开合。

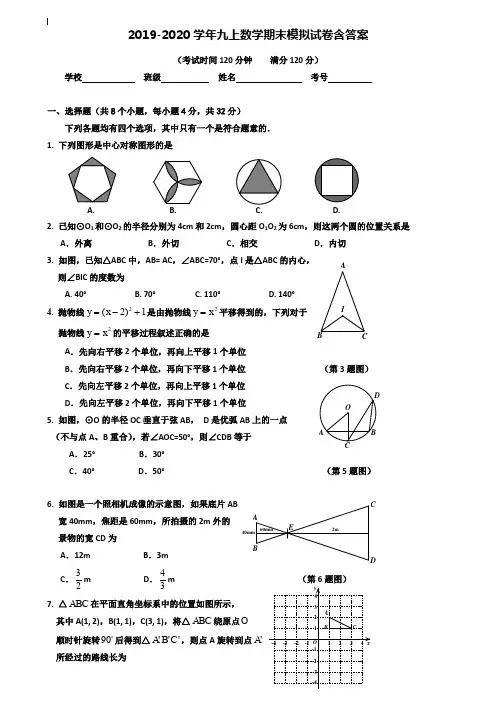
2019-2020学年九上数学期末模拟试卷含答案（考试时间120分钟 满分120分）学校 班级 姓名 考号一、选择题（共8个小题，每小题4分，共32分）下列各题均有四个选项，其中只有一个是符合题意的． 1. 下列图形是中心对称图形的是A. B.D.2. 已知⊙O 1和⊙O 2的半径分别为4cm 和2cm ，圆心距O 1O 2为6cm ，则这两个圆的位置关系是 A ．外离B ．外切C ．相交D ．内切3. 如图，已知△ABC 中，AB= AC ，∠ABC=70°，点I 是△ABC 的内心， 则∠BIC 的度数为A. 40°B. 70°C. 110°D. 140° 4. 抛物线1)2(2+-=x y 是由抛物线2x y =平移得到的，下列对于 抛物线2x y =的平移过程叙述正确的是 A ．先向右平移2个单位，再向上平移1个单位B ．先向右平移2个单位，再向下平移1个单位 （第3题图）C ．先向左平移2个单位，再向上平移1个单位D ．先向左平移2个单位，再向下平移1个单位5. 如图，⊙O 的半径OC 垂直于弦AB ， D 是优弧AB 上的一点 （不与点A 、B 重合），若∠AOC=50°，则∠CDB 等于A ．25°B ．30°C ．40°D ．50° （第5题图）6. 如图是一个照相机成像的示意图，如果底片AB 宽40mm ，焦距是60mm ，所拍摄的2m 外的 景物的宽CD 为A ．12mB ．3mC ．23m D ．34m （第6题图） 7. △ABC 在平面直角坐标系中的位置如图所示， 其中A(1, 2)，B(1, 1)，C(3, 1)，将△ABC 绕原点O 顺时针旋转90后得到△'''C B A ，则点A 旋转到点'A 所经过的路线长为A ．π25B ．π45 C ．π25D ．（第7题图） 8. 如图，Rt △ABC 中，∠C ＝90°，AC ＝3，BC ＝4，P 是斜边AB 上一动点（不与点A 、B 重合），PQ ⊥AB 交△ABC 的直角边于 点Q ，设AP 为x ，△APQ 的面积为y ，则下列图象中，能表示 y 关于x 的函数关系的图象大致是A. B. C. D. 二、填空题（共4个小题，每小题4分，共16分）9. 如图，△ABC 为等边三角形，D 是△ABC 内一点，且AD ＝3，将△ABD 绕点A 旋转到△ACE 的位置，连接DE ，则DE 的长为 .（第9题图）（第11题图）10. 如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型．若该圆的半径为1，扇形的圆心角等于60°，则这个扇形的半径R 的值是 .11. 如图，梯形ABCD 中，AD ∥BC ，∠C=90°，AB=AD=4，BC=6，以点A 为圆心在这个梯形内画出一个最大的扇形（图中阴影部分），则这个扇形的面积是 ．12. 古希腊著名的毕达哥拉斯学派把1，3，6，10 ，… 这样的数称为“三角形数”（如图①），而把1，4，9，16，…这样的数称为“正方形数”（如图②）． 如果规定11a =，23a =，36a =，410a =，…；11b =，24b =，39b =，416b =，…；1112y a b =+，2222y a b =+，3332y a b =+，4442y a b =+，…，那么，按此规定，=6y ，n y ＝ （用含n 的式子表示，n 为正整数）．三、解答题（共13个小题，共72 分） 13.（本小题满分5分）计算：︒-︒+︒30cos 245sin 60tan 2.y 5Ox14916图②图①10631y O14.（本小题满分5分）如图，已知4=AC ，求AB 和BC 的长.15.（本小题满分5分）如图，□ABCD 中，点E 在BA 的延长线上， 连接CE ，与AD 相交于点F. （1）求证：△EBC ∽△CDF ；（2）若BC ＝8，CD ＝3，AE ＝1，求AF 的长．16.（本小题满分4分）如图，在平面直角坐标系中，△ABC 和△'''C B A 是以 坐标原点O 为位似中心的位似图形，且点B （3，1）， B′（6，2）.（1）若点A （25，3），则A′的坐标为 ；（2）若△ABC 的面积为m ，则△A ′B ′C ′的面积＝ .17.（本小题满分5分）二次函数2y ax bx c =++的部分图象如图所示，其中图象与 x 轴交于点A （－1,0），与y 轴交于点C （0，－5），且经过点 D （3，－8）.（1）求此二次函数的解析式；（2）将此二次函数的解析式写成2()y a x h k =-+的形式，并直接写出此二次函数图象的顶点坐标以及它与x 轴的另一个交点B 的坐标.18. （本小题满分5分）经过18个月的精心酝酿和290多万首都市民投票参与，，“北京精神”表述语“爱国、创新、包容、厚德”正式向社会发布. 为了更好地宣传“北京精神”，小明同学参加了由街道组织的百姓宣讲小分队，利用周末时间到周边社区发放宣传材料. 第一周发放宣传材料300份，第三周发放宣传材料363份. 求发放宣传材料份数的周平均增长率.19. （本小题满分5分）如图，CD 与AB 是⊙O 内两条相交的弦，且AB 为⊙O 的直径， CE ⊥AB 于点E ，CE=5，连接AC 、BD. （1）若135sin =D ，则cosA= ；（2）在（1）的条件下，求BE 的长．A20. （本小题满分5分）小红在学习了教科书上相关内容后自制了一个测角仪（图①），并尝试用它来测量校园内一座教学楼CD 的高度（如图②）.她先在A 处测得楼顶C 的仰角=α30°，再向楼的方向直行10米到达B 处，又测得楼顶C 的仰角=β60°，若小红的目高（眼睛到地面的高度）AE 为1.60米，请你帮助她计算出这座教学楼CD 的高度（结果精确到0.1米，参考数据：41.12≈，73.13≈，24.25≈）.图① 图②21.（本小题满分5分）已知抛物线4)1(21-+++=m x m x y 与x（1）求m 的值； （2）画出这条抛物线；（2）若直线b kx y +=2过点B P （－2m ，－3m ），根据图象回答：当x 取什么值时，1y ≥2y .22. （本小题满分6分）某超市销售一款进价为50元/调查发现：以60元/个的价格销售，平均每周销售书包100个；若每个书包的销售价格每提高1元，则平均每周少销售书包2个.（1）求该超市这款书包平均每周的销售量y （个）与销售价x （元/个）之间的函数关系式； （2）求该超市这款书包平均每周的销售利润w （元）与销售价x （元/个）之间的函数关系式； （3）当每个书包的销售价为多少元时，该超市这款书包平均每周的销售利润最大？最大利润是多少元？23.（本小题满分6分）如图，在△ABC 中，∠ACB=90°，O 为BC 边上一点， 以O 为圆心，OB 为半径作半圆与AB 边和BC 边分别 交于点D 、点E ，连接CD ，且CD=CA ，BD=56， tan ∠ADC=2．（1）求证：CD 是半圆O 的切线；BC A（3）求AD 的长.24. （本小题满分8分）已知，在△ABC 中，∠BAC=90°，AB=AC ，BC=22，点D 、E 在BC 边上（均不与点B 、C 重合，点D 始终在点E 左侧），且∠DAE ＝45°．（1）请在图①中找出两对相似但不全等的三角形，写在横线上 ， ； （2）设BE ＝m ，CD ＝n ，求m 与n 的函数关系式，并写出自变量n 的取值范围； （3）如图②，当BE ＝CD 时，求DE 的长；（4）求证：无论BE 与CD 是否相等，都有DE 2=BD 2+CE 2.图① 图② 备用图25.（本小题满分8分）已知抛物线y ＝ax 2＋bx ＋6与x 轴交于A 、B 两点（点A 在原点的左侧，点B 在原点的右侧），与y 轴交于点C ，且OB=21OC ，tan ∠ACO=61，顶点为D ．（2）求直线CD 与x 轴的交点E 的坐标.（3）在此抛物线上是否存在一点F ，使得以点A 、C 、E 、F 为顶点的四边形是平行四边形？若存在，请求出点F 的坐标；若不存在，请说明理由．（4）若点M （2，y ）是此抛物线上一点，点N 是直线AM 上方的抛物线上一动点，当点N 运动到什么位置时，四边形ABMN 的面积S 最大? 请求出此时S 的最大值和点N 的坐标．（5）点P 为此抛物线对称轴上一动点，若以点P 为圆心的圆与（4）中的直线AM 及x 轴同时相切，则此时点P 的坐标为 .备用图① 备用图②数学试卷 参考答案及评分标准一、选择题（共8个小题，每小题4分，共32分）题号12345678答案D B C A A D A C二、填空题（共4个小题，每小题4分，共16分） 9. 3 10. 6 11.π4 12. 78，n n +22（每空2分）三、解答题（共13个小题，共72 分） 13.（本小题满分5分）解： 2322232⨯-⎪⎪⎭⎫ ⎝⎛+=原式，……………………………………………3分 21=. ……………………………………………………………………5分14.（本小题满分5分） 解：作CD ⊥AB 于点D ， 在Rt △ACD 中，∵∠A ＝30°， ∴∠ACD ＝90°－∠A ＝60°，221==AC CD ， 32cos =⋅=A AC AD . ……………………………………………………………3分在Rt △CDB 中，∵∠DCB ＝∠ACB －∠ACD ＝45°， ∴2==CD BD ，2245sin =︒=CDBC . …………………………………………………………………4分∴322+=+=BD AD AB .…………………………………………………………5分15.（本小题满分5分）（1）证明：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AB ∥CD.∴△EAF ∽△EBC ，△EAF ∽△CDF. ……………………………………………2分 ∴△EBC ∽△CDF. …………………………………………………………………3分（2）解：∵△EAF ∽△EBC ，∴BC AF EB EA =，即8311AF=+. 解得2=AF . …………………………………………………………………………5分16. （本小题满分4分）（1）（5，6）；…………………………………………………………………………………2分（2） 4m. ……………………………………………………………………………………4分17. （本小题满分5分） 解：（1）由题意，有⎪⎩⎪⎨⎧-=++-==+-.839,5,0c b a c c b a 解得 ⎪⎩⎪⎨⎧-=-==.5,4,1c b a ∴此二次函数的解析式为542--=x x y . …………………………………2分（2）9)2(2--=x y ，顶点坐标为（2，－9），B （5，0）. …………………………5分18. （本小题满分5分）解：设发放宣传材料份数的周平均增长率为x ，由题意，有.363)1(3002=+x …………………………………………………………………3分 解得 1.01=x ，1.22-=x . …………………………………………………………4分 ∵1.2-=x <0，不符合题意，舍去，∴%101.0==x . ……………………………………………………………………5分 答：这两次发放材料数的平均增长率为10%.19. （本小题满分5分） （1）1312. …………………………………………………………………………………2分 （2）解：如图，连接BC.∵AB 为⊙O 的直径，∴∠ACB ＝90°. ∴由（1）知AC ＝13， 12=AE ，1312cos =A . 在Rt △ACB 中，ABACA =cos ，∴12169=AB . ………………………………………………………………………4分 ∴1225=-=AE AB BE . …………………………………………………………5分20.（本小题满分5分）解：∵=α30°，=β60°，∴∠ECF ＝αβ-＝30°. ∴10==EF CF .在Rt △CFG 中，.35cos =⋅=βCF CG ……………………………………………3分 ∴3.106.135≈+=+=GD CG CD . ………………………………………………5分 答：这座教学楼的高度约为10.3米.A21.（本小题满分5分） 解：（1）由题意，有121-=+-m ，解得m ＝1. ……………………………………………………………2分（2）如图1；…………………3分图1图2（3）如图2，x ≤－2或x ≥1. ……………………………………………………………5分22.（本小题满分6分）解：（1）由题意，有 )60(2100--=x y ，即2202+-=x y ；………………………………………………………………………2分 （2）由题意，有 )2202)(50(+--=x x w ，即1100032022-+-=x x w ；…………………………………………………………4分（3）∵抛物线1100032022-+-=x x w 的开口向下，在对称轴80=x 的左侧，w 随x 的增大而增大. 由题意可知7060≤≤x ，………………………………………………………………5分 ∴当70=x 时，w 最大为1600. ………………………………………………………6分 因此，当每个书包的销售价为70元时，该超市可以获得每周销售的最大利润1600元.23.（本小题满分6分） （1）证明：如图，连接OD ，∵OD ＝OB ，∴∠1＝∠2. ∵CA ＝CD ，∴∠ADC ＝∠A. 在△ABC 中，∵∠ACB ＝90°，∴∠A ＋∠1＝90°. ∴∠ADC ＋∠2＝90°. ∴∠CDO ＝90°. ∵OD 为半圆O 的半径，∴CD 为半圆O 的切线. ………………………………………………………………2分 （2）解：如图，连接DE.BPA∵BE 为半圆O 的直径， ∴∠EDB ＝90°. ∴∠1＋∠3＝90°. ∴∠ADC ＝∠3. ∴23tan ==∠EDBD. ∴53=ED . ∴1522=+=DE BD EB . ………………………………………………………4分（3）解：作CF ⊥AD 于点F ，∴AF ＝DF.设x DF =，∵2tan =∠ADC ，∴CF ＝2x. ∵∠1＋∠FCB ＝90°， ∴ADC FCB ∠=∠. ∴2tan =∠FCB . ∴FB ＝4x. ∴BD ＝3 x ＝56. 解得52=x .∴A D ＝2D F ＝2x ＝54. ……………………………………………………………6分24.（本小题满分8分）解：（1）△ADE ∽△BAE ，△ADE ∽△CDA ，△BAE ∽△CDA ；（写出任意两对即可） （2）∵∠BAC ＝90°，AB ＝AC ，BC ＝22，由（1）知 △BAE ∽△CDA ， ∴CABECD BA =. ∴22m n =. ∴nm 4= （222<<n ）. ……………………………………4分（3）由（2）只BE·CD ＝4，∴BE ＝CD ＝2.∴BD ＝BC －CD ＝222-.∴DE ＝BE －BD ＝224-.………………………………………………………5分 （4）如图，依题意，可以将△AEC 绕点A 顺时针旋转90°至△AFB 的位置，则FB ＝CE ，AF ＝AE ，∠1＝∠2， ∴∠FBD ＝90°.∴22222CE BD FB BD DF +=+=. (6)∵∠3＋∠1＝∠3＋∠2＝45°， ∴∠FAD ＝∠DAE. 又∵AD ＝AD ，AF ＝AE ， ∴△AFD ≌△AED.∴DE ＝DF. ………………………………………………………………………7分 ∴222CE BD DE +=. …………………………………………………………8分25.（本小题满分8分）解：（1）根据题意，得C （0,6）.在Rt △AOC 中，61tan =∠ACO ，OC ＝6， ∴OA ＝1. ∴A （－1,0）. ……………………………………………………………1分 （2）∵OC OB 21=，∴OB ＝3. ∴B （3,0）. 由题意，得 ⎩⎨⎧=++=+-.0639,06b a b a 解得⎩⎨⎧=-=.4,2b a ∴6422++-=x x y .∴D （1,8）. ……………………………………………………………………2分 可求得直线CD 的解析式为62+=x y .∴E （－3,0）. ……………………………………………………………………3分 （3）假设存在以点A 、C 、F 、E 为顶点的平行四边形，则F 1（2,6），F 2（－2,6），F 3（－4,－6）.经验证，只有点（2,6）在抛物线6422++-=x x y 上，∴F （2,6）. ………………………………………………………………………4分（4）如图，作NQ ∥y 轴交AM 于点Q ，设N （m, 6422++-m m ）.当x ＝2时，y ＝6，∴M （2,6）. 可求得直线AM 的解析式为22+=x y . ∴Q （m ，2m ＋2）.∴NQ ＝422)22(64222++-=+-++-m m m m m . ∵AMN ABM S S S ∆∆+=，其中126421=⨯⨯=∆ABM S ， ∴当AMN S ∆最大时，S 值最大. ∵MNQ ANQ AMN S S S ∆∆∆+=)422(3212++-⨯⨯=m m , 6332++-=m m ,427)21(32+--=m .∴当21=m 时，AMN S ∆的最大值为427. ∴S 的最大值为475.……………………………………………………………………6分 当21=m 时，2156422=++-m m . ∴N （21，215）. ……………………………………………………………………7分 （5）P 1（1，15-），P 2（1，15--）. …………………………………………8分说明：写成P 1（1，154+），P 2（1，154--）不扣分.2019-2020学年九上数学期末模拟试卷含答案一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．1．如果3x=4y（y≠0），那么下列比例式中正确的是（）A．B．C．D．2．在Rt△ABC中，∠C=90°，，AC=2，则tanA的值为（）A．B．2 C．D．3．如图，AB是⊙O的直径，点C、D在⊙O上．若∠ACD=25°，则∠BOD的度数为（）A．100°B．120°C．130°D．150°4．如图，在⊙O中，弦AB垂直平分半径OC．若⊙O的半径为4，则弦AB的长为（）A．B．C．D．5．如果在二次函数的表达式y=ax2+bx+c中，a＞0，b＜0，c＜0，那么这个二次函数的图象可能是（）A．B．C．D．6．若二次函数y=x2+2x+m的图象与坐标轴有3个交点，则m的取值范围是（）A．m＞1 B．m＜1 C．m＞1且m≠0 D．m＜1且m≠07．如图，将函数的图象沿y轴向上平移得到新函数图象，其中原函数图象上的两点A（1，m）、B（4，n）平移后对应新函数图象上的点分别为点A′、B′．若阴影部分的面积为6，则新函数的表达式为（）A．B．C．D．8．如图，点M为▱ABCD的边AB上一动点，过点M作直线l垂直于AB，且直线l与▱ABCD的另一边交于点N．当点M从A→B匀速运动时，设点M的运动时间为t，△AMN的面积为S，能大致反映S与t函数关系的图象是（）A．B．C．D．二、填空题（本题共16分，每小题2分）9．如果两个相似三角形的周长比为2：3，那么这两个相似三角形的面积比为．10．如图，在△ABC中，点D、E分别在边AB、AC上．若∠ADE=∠C，AB=6，AC=4，AD=2，则EC=．11．如图，扇形的圆心角∠AOB=60°，半径为3cm．若点C、D是的三等分点，则图中所有阴影部分的面积之和是cm2．12．“平改坡”是指在建筑结构许可条件下，将多层住宅的平屋顶改建成坡屋顶，并对外立面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为．如图是某小区对楼顶进行“平改坡”改造的示意图．根据图中的数据，如果要使坡面BC的坡度达到1：1.2，那么立柱AC的长为米．13．如图，一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A和点B．当y1＞y2＞0时，x的取值范围是．14．如图，在Rt△ABC中，∠C=90°，AB=10，若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，则AC的长等于．15．如图，在平面直角坐标系xOy中，△ABC经过若干次图形的变化（平移、轴对称、旋转）得到△DEF，写出一种由△ABC得到△DEF的过程：．16．石景山区八角北路有一块三角形空地（如图1）准备绿化，拟从点A出发，将△ABC分成面积相等的三个三角形，栽种三种不同的花草．下面是小美的设计（如图2）．作法：（1）作射线BM；（2）在射线BM上顺次截取BB1=B1B2=B2B3；（3）连接B3C，分别过B1、B2作B1C1∥B2C2∥B3C，交BC于点C1、C2；（4）连接AC1、AC2．则．请回答，成立的理由是：①；②．三、解答题（本题共68分）解答应写出文字说明，演算步骤或证明过程.17．（5分）计算：3tan30°﹣cos245°+﹣2sin60°．18．（5分）用配方法求二次函数y=x2﹣10x+3的顶点坐标．19．（5分）在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c．若a=2，sin，求b和c．20．（5分）小红和小丁玩纸牌游戏：如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小丁从剩余的3张牌中也抽出一张．比较两人抽出的牌面上的数字，数字大者获胜．（1）请用树状图或列表法表示出两人抽牌可能出现的所有结果；（2）这个游戏公平吗？请说明理由．21．（5分）如图，小明想测量山的高度．他在点B处仰望山顶A，测得仰角∠ABN=30°，再向山的方向（水平方向）行进100m至索道口点C处，在点C处仰望山顶A，测得仰角∠ACN=45°．求这座山的高度．（结果精确到0.1m，小明的身高忽略不计）（参考数据：≈1.41，≈1.73）22．（5分）在平面直角坐标系xOy中，一次函数y=x+b的图象与x轴交于点A（2，0），与反比例函数y=的图象交于点B（3，n）．（1）求一次函数与反比例函数的表达式；（2）若点P为x轴上的点，且△PAB的面积是2，则点P的坐标是．23．（5分）如图，四边形ABCD是平行四边形，CE⊥AD于点E，DF⊥BA交BA的延长线于点F．（1）求证：△ADF∽△DCE；（2）当AF=2，AD=6，且点E恰为AD中点时，求AB的长．24．（5分）二次函数y=x2﹣2mx+5m的图象经过点（1，﹣2）．（1）求二次函数图象的对称轴；（2）当﹣4≤x≤1时，求y的取值范围．25．（6分）如图，AC是⊙O的直径，点D是⊙O 上一点，⊙O的切线CB与AD的延长线交于点B，点F 是直径AC上一点，连接DF并延长交⊙O于点E，连接AE．（1）求证：∠ABC=∠AED；（2）连接BF，若AD=，AF=6，tan∠AED=，求BF的长．26．（7分）在平面直角坐标系xOy中，抛物线y=﹣x2+mx+n经过点A（﹣1，0）和B（0，3）．（1）求抛物线的表达式；（2）抛物线与x轴的正半轴交于点C，连接BC．设抛物线的顶点P关于直线y=t的对称点为点Q，若点Q 落在△OBC的内部，求t的取值范围．27．（7分）在正方形ABCD中，点P在射线AC上，作点P关于直线CD的对称点Q，作射线BQ交射线DC于点E，连接BP．（1）当点P在线段AC上时，如图1．①依题意补全图1；②若EQ=BP，则∠PBE的度数为，并证明；（2）当点P在线段AC的延长线上时，如图2．若EQ=BP，正方形ABCD的边长为1，请写出求BE长的思路．（可以不写出计算结果）28．（8分）在平面直角坐标系xOy中，点P的坐标为（x1，y1），点Q的坐标为（x2，y2），且x1≠x2，y1≠y2，若PQ为某个等腰三角形的腰，且该等腰三角形的底边与x轴平行，则称该等腰三角形为点P，Q的“相关等腰三角形”．下图为点P，Q的“相关等腰三角形”的示意图．（1）已知点A的坐标为（0，1），点B的坐标为，则点A，B的“相关等腰三角形”的顶角为°；（2）若点C的坐标为，点D在直线y=4上，且C，D的“相关等腰三角形”为等边三角形，求直线CD的表达式；（3）⊙O的半径为，点N在双曲线y=﹣上．若在⊙O上存在一点M，使得点M、N的“相关等腰三角形”为直角三角形，直接写出点N的横坐标x N的取值范围．参考答案与试题解析一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合题意的选项只有一个．1．如果3x=4y（y≠0），那么下列比例式中正确的是（）A．B．C．D．【分析】根据比例的性质，可得答案．【解答】解：A、由比例的性质，得4x=3y与3x=4y不一致，故A不符合题意；B、由比例的性质，得xy=12与3x=4y不一致，故B不符合题意；C、由比例的性质，得4x=3y与3x=4y不一致，故C不符合题意；D、由比例的性质，得3x=4y与3x=4y一致，故D符合题意；故选：D．【点评】本题考查了比例的性质，利用比例的性质是解题关键．2．在Rt△ABC中，∠C=90°，，AC=2，则tanA的值为（）A．B．2 C．D．【分析】本题需先根据已知条件，得出BC的长，再根据正切公式即可求出答案．【解答】解：∵∠C=90°，AB=，AC=2，∴BC=1，∴tanA==．故选：A．【点评】本题主要考查了锐角三角函数的定义，在解题时要根据在直角三角形中，正切等于对边比邻边这个公式计算是本题的关键．3．如图，AB是⊙O的直径，点C、D在⊙O上．若∠ACD=25°，则∠BOD的度数为（）A．100°B．120°C．130°D．150°【分析】根据圆周角定理求出∠AOD即可解决问题．【解答】解：∵∠AOD=2∠ACD，∠ACD=25°，∴∠AOD=50°，∴∠BOD=180°﹣∠AOD=180°﹣50°=130°，故选：C．【点评】本题考查圆周角定理，邻补角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．4．如图，在⊙O中，弦AB垂直平分半径OC．若⊙O的半径为4，则弦AB的长为（）A．B．C．D．【分析】连接OA，由AB垂直平分OC，求出OD的长，再利用垂径定理得到D为AB的中点，在直角三角形AOD中，利用垂径定理求出AD的长，即可确定出AB的长．【解答】解：连接OA，由AB垂直平分OC，得到OD=OC=2，∵OC⊥AB，∴D为AB的中点，则AB=2AD=2=2=4．故选：B．【点评】此题考查了垂径定理，以及勾股定理，根据题意作出辅助线，构造出直角三角形是解本题的关键．5．如果在二次函数的表达式y=ax2+bx+c中，a＞0，b＜0，c＜0，那么这个二次函数的图象可能是（）A．B．C．D．【分析】由a＞0，b＜0，c＜0，推出﹣＞0，可知抛物线的图象开口向上，对称轴在y轴的右边，交y 轴于负半轴，由此即可判断．【解答】解：∵a＞0，b＜0，c＜0，∴﹣＞0，∴抛物线的图象开口向上，对称轴在y轴的右边，交y轴于负半轴，故选：C．【点评】本题考查二次函数的图象，解题的关键是熟练掌握基本知识，灵活运用所学知识解决问题，属于中考常考题型．6．若二次函数y=x2+2x+m的图象与坐标轴有3个交点，则m的取值范围是（）A．m＞1 B．m＜1 C．m＞1且m≠0 D．m＜1且m≠0【分析】由抛物线与坐标轴有三个交点可得出：方程x2+2x+m=0有两个不相等的实数根，且m≠0，利用根的判别式△＞0可求出m的取值范围，此题得解．【解答】解：∵二次函数y=x2+2x+m的图象与坐标轴有3个交点，∴方程x2+2x+m=0有两个不相等的实数根，且m≠0，∴△=22﹣4m＞0，∴m＜1．∴m＜1且m≠0．故选：D．【点评】本题考查了抛物线与x轴的交点以及根的判别式，利用根的判别式△＞0找出关于m的一元一次不等式是解题的关键．7．如图，将函数的图象沿y轴向上平移得到新函数图象，其中原函数图象上的两点A（1，m）、B（4，n）平移后对应新函数图象上的点分别为点A′、B′．若阴影部分的面积为6，则新函数的表达式为（）A．B．C．D．【分析】先根据二次函数图象上点的坐标特征求出A、B两点的坐标，再过A作AC∥x轴，交B′B的延长线于点C，则C（4，1），AC=4﹣1=3，根据平移的性质以及曲线段AB扫过的面积为6（图中的阴影部分），得出AA′=2，然后根据平移规律即可求解．【解答】解：∵函数y=（x﹣2）2+1的图象过点A（1，m），B（4，n），∴m=（1﹣2）2+1=1，n=（4﹣2）2+1=2，∴A（1，1），B（4，2），过A 作AC ∥x 轴，交B′B 的延长线于点C ，则C （4，1）， ∴AC=4﹣1=3，∵曲线段AB 扫过的面积为6（图中的阴影部分）， ∴AC•AA′=3AA′=6， ∴AA′=2，即将函数y=（x ﹣2）2+1的图象沿y 轴向上平移2个单位长度得到一条新函数的图象，∴新图象的函数表达式是y=（x ﹣2）2+3． 故选：B ．【点评】此题主要考查了二次函数图象与几何变换以及平行四边形面积求法等知识，根据已知得出AA′是解题关键．8．如图，点M 为▱ABCD 的边AB 上一动点，过点M 作直线l 垂直于AB ，且直线l 与▱ABCD 的另一边交于点N ．当点M 从A→B 匀速运动时，设点M 的运动时间为t ，△AMN 的面积为S ，能大致反映S 与t 函数关系的图象是（ ）A ．B ．C ．D ．【分析】当点N 在AD 上时，可得前半段函数图象为开口向上的抛物线的一部分；当点N 在DC 上时，MN 长度不变，可得后半段函数图象为一条线段．【解答】解：设∠A=α，点M 运动的速度为a ，则AM=at ， 当点N 在AD 上时，MN=tanα×AM=tanα•at ，此时S=×at ×tanα•at=tanα×a 2t 2，∴前半段函数图象为开口向上的抛物线的一部分， 当点N 在DC 上时，MN 长度不变，此时S=×at ×MN=a ×MN ×t ， ∴后半段函数图象为一条线段， 故选：C ．【点评】本题主要考查了动点问题的函数图象，用图象解决问题时，要理清图象的含义即会识图．函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．二、填空题（本题共16分，每小题2分）9．如果两个相似三角形的周长比为2：3，那么这两个相似三角形的面积比为4：9．【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答．【解答】解：因为两个相似三角形的周长比为2：3，所以这两个相似三角形的相似比为2：3，所以这两个相似三角形的面积比为4：9；故答案为：4：9．【点评】本题考查的是相似三角形的性质，相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．10．如图，在△ABC中，点D、E分别在边AB、AC上．若∠ADE=∠C，AB=6，AC=4，AD=2，则EC=1．【分析】只要证明△ADE∽△ACB，推出=，求出AE即可解决问题；【解答】解；∵∠A=∠A，∠ADE=∠C，∴△ADE∽△ACB，∴=，∴=，∴AE=3，∴EC=AC﹣AE=4﹣3=1，故答案为1．【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型．11．如图，扇形的圆心角∠AOB=60°，半径为3cm．若点C、D是的三等分点，则图中所有阴影部分的面积之和是cm2．【分析】由题意可知C、D是弧AB的三等分点，通过平移可把阴影部分都集中到一个小扇形中，可发现阴影部分正好是扇形AOB的，先求出扇形AOB的面积再求阴影部分的面积或者直接求圆心角是20度，半径是3的扇形的面积皆可．【解答】解：S扇形OAB=，S阴影=S扇形OAB=×π=π．故答案为：【点评】此题考查扇形的面积问题，通过平移的知识把小块的阴影部分集中成一个规则的图形﹣﹣扇形，再求算扇形的面积即可．利用平移或割补把不规则图形变成规则图形求面积是常用的方法．12．“平改坡”是指在建筑结构许可条件下，将多层住宅的平屋顶改建成坡屋顶，并对外立面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为．如图是某小区对楼顶进行“平改坡”改造的示意图．根据图中的数据，如果要使坡面BC的坡度达到1：1.2，那么立柱AC的长为 2.5米．【分析】由坡度的概念得出=，根据AB=3可得AC的长度．【解答】解：根据题意知=，∵AB=3，∴=，解得：AC=2.5，故答案为：2.5．【点评】本题主要考查解直角三角形的应用﹣坡度坡角问题，解题的关键是熟练掌握坡度的定义．13．如图，一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A和点B．当y1＞y2＞0时，x的取值范围是﹣2＜x＜﹣0.5．【分析】根据一次函数与反比例函数交点纵坐标，结合图象确定出所求x的范围即可．【解答】解：根据图象得：当y1＞y2＞0时，x的取值范围是﹣2＜x＜﹣0.5，故答案为：﹣2＜x＜﹣0.5【点评】此题考查了反比例函数与一次函数的交点问题，利用了数形结合的思想，弄清数形结合思想是解本题的关键．14．如图，在Rt△ABC中，∠C=90°，AB=10，若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，则AC的长等于5．【分析】连接CD，根据直角三角形斜边上的中线等于斜边的一半可得AB=2CD，求出圆的半径的长，再利用勾股定理列式进行计算即可得解．【解答】解：如图，∵∠C=90°，点D为AB的中点，∴AB=2CD=10，∴CD=5，∴BC=CD=5，在Rt△ABC中，AC===5．故答案为：5．【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理的应用，求出圆的半径的长是解题的关键．15．如图，在平面直角坐标系xOy中，△ABC经过若干次图形的变化（平移、轴对称、旋转）得到△DEF，写出一种由△ABC得到△DEF的过程：向右平移4个单位，沿对称轴BC翻折，再绕点C逆时针旋转90°．【分析】根据对应点C与点F的位置，结合两三角形在格结构中的位置解答．【解答】解：△ABC向右平移4个单位，沿对称轴BC翻折，再绕点C逆时针旋转90°即可得到△DEF，所以，过程为：向右平移4个单位，沿对称轴BC翻折，再绕点C逆时针旋转90°．故答案为：向右平移4个单位，沿对称轴BC翻折，再绕点C逆时针旋转90°．【点评】本题考查了几何变换的类型，平移、旋转，准确识图是解题的关键．16．石景山区八角北路有一块三角形空地（如图1）准备绿化，拟从点A出发，将△ABC分成面积相等的三个三角形，栽种三种不同的花草．下面是小美的设计（如图2）．作法：（1）作射线BM；（2）在射线BM上顺次截取BB1=B1B2=B2B3；（3）连接B3C，分别过B1、B2作B1C1∥B2C2∥B3C，交BC于点C1、C2；（4）连接AC1、AC2．则．请回答，成立的理由是：①平行线分线段成比例定理；②等底共高．【分析】根据平行线分线段成比例定理和等底共高求解可得．【解答】解：由BB1=B1B2=B2B3且B1C1∥B2C2∥B3C，依据平行线分线段成比例定理知BC1=C1C2=C2C，再由△ABC1，△AC1C2与△AC2C等底共高知，故答案为：①平行线分线段成比例定理；②等底共高．【点评】本题主要考查作图﹣应用与设计作图，解题的关键是掌握平行线分线段成比例定理和等底共高的两三角形面积关系．三、解答题（本题共68分）解答应写出文字说明，演算步骤或证明过程.17．（5分）计算：3tan30°﹣cos245°+﹣2sin60°．【分析】根据特殊角三角函数值，可得答案．【解答】解：原式=3×﹣（）2+﹣2×=﹣+2﹣=．【点评】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键．18．（5分）用配方法求二次函数y=x2﹣10x+3的顶点坐标．【分析】把解析式化为顶点式即可．【解答】解：∵y=x2﹣10x+3=（x﹣5）2﹣22，∴二次函数的顶点坐标为（5，﹣22）．【点评】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a（x﹣h）2+k中，顶点坐标为（h，k），对称轴为x=h．19．（5分）在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c．若a=2，sin，求b和c．【分析】先根据sinA=知c==6，再根据勾股定理求解可得．【解答】解：如图，∵a=2，sin，∴c===6，则b===4．【点评】本题主要考查锐角三角函数的定义，解题的关键是掌握正弦函数的定义及勾股定理．20．（5分）小红和小丁玩纸牌游戏：如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小丁从剩余的3张牌中也抽出一张．比较两人抽出的牌面上的数字，数字大者获胜．（1）请用树状图或列表法表示出两人抽牌可能出现的所有结果；（2）这个游戏公平吗？请说明理由．【分析】（1）根据题意画出树状图，即可解决问题；（2）根据树状图，利用概率公式即可求得小红获胜的概率，由概率相等，即可判定这个游戏公平；【解答】解：（1）树状图如右：则小红获胜的概率：=，小丁获胜的概率：=，所以这个游戏比较公平．【点评】本题考查的是用列表法与树状图法求事件的概率，解题的关键是学会正确画出树状图，判断游戏。