洛必达法则word版
- 格式:doc
- 大小:219.50 KB
- 文档页数:6
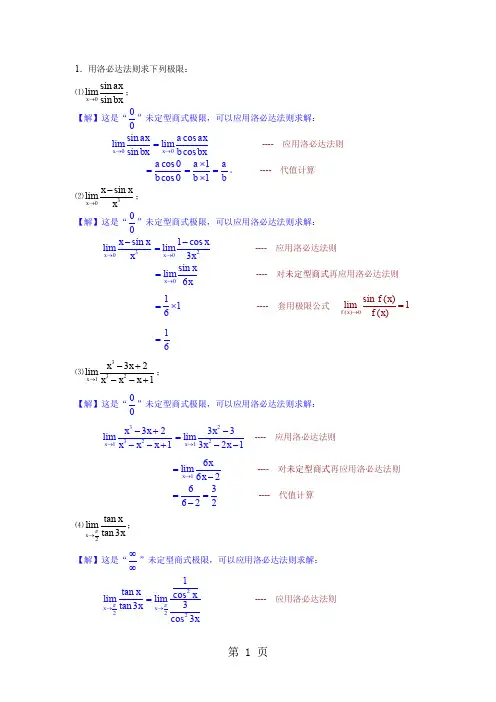
1.用洛必达法则求下列极限:⑴0sin limsin x axbx→;【解】这是“00”未定型商式极限,可以应用洛必达法则求解:0sin lim sin x ax bx →0cos limcos x a axb bx→= ---- 应用洛必达法则 cos 0cos 0a b =11a b ⨯=⨯ab=。
---- 代值计算 ⑵30sin lim x x x x→-; 【解】这是“00”未定型商式极限,可以应用洛必达法则求解:30sin lim x x x x →-201cos lim3x xx →-= ---- 应用洛必达法则 0sin lim6x xx→= ---- 对未定型商式再应用洛必达法则 116=⨯ ---- 套用极限公式 ()0sin ()lim1()f x f x f x →= 16=⑶332132lim 1x x x x x x →-+--+; 【解】这是“”未定型商式极限,可以应用洛必达法则求解: 332132lim 1x x x x x x →-+--+22133lim 321x x x x →-=-- ---- 应用洛必达法则 16lim62x xx →=- ---- 对未定型商式再应用洛必达法则63622==- ---- 代值计算 ⑷2tan limtan 3x xxπ→; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2tan lim tan 3x xx π→2221cos lim 3cos 3x x xπ→= ---- 应用洛必达法则222cos 3lim3cos x xx π→= ---- 整理繁分式 22cos3(sin 3)3lim32cos (sin )x x x x x π→⋅-⋅=⋅⋅- ---- 对未定型商式再应用洛必达法则2sin 6limsin 2x xxπ→= ---- 化简复杂分式 26cos6lim2cos 2x xxπ→= ---- 对未定型商式再应用洛必达法则3cos3cos ππ=---- 代值计算3=⑸2(ln )lim x x x→+∞; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2(ln )limx x x→+∞12ln lim 12x x x x→+∞⋅= ---- 应用洛必达法则 4ln limx xx→+∞= ---- 化简繁分式14lim 12x x x→+∞= ---- 对未定型商式再应用洛必达法则 8limx x→+∞= ---- 化简繁分式 0=⑹2ln()2lim tan x x x ππ+→-; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解:2ln()2lim tan x x x ππ+→-2212lim 1cos x x xππ+→-= ---- 应用洛必达法则 22cos lim 2x x x ππ+→=----- 化简繁分式22cos (sin )lim 1x x x π+→-= ---- 对未定型商式再应用洛必达法则2cossin22ππ=-0= ---- 代入计算⑺212lim x x x e →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:212lim xx x e →2102lim 1x x e x →= ---- 化为商式后,成为“∞∞”未定型商式极限 212021()'lim1()'x x e x x→= ---- 应用洛必达法则 2211lim x x e →+∞= ---- 化简繁分式 =+∞ ---- 代入计算⑻0lim cot x x x →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:lim cot x x x →0limtan x xx →= ---- 化为商式后,成为“∞∞”未定型商式极限021lim 1cos x x →= ---- 应用洛必达法则 20limcos x x →= ---- 化简繁分式2cos 01== ---- 代入计算⑼2lim(sec tan )x x x π→-;【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:2lim(sec tan )x x x π→-21sin lim()cos cos x x x xπ→=- ---- 为通分化为商式作准备 21sin limcos x xx π→-= ---- 成为“00”未定型商式极限2cos limsin x xxπ→-=- ---- 应用洛必达法则cos 20sin2ππ== ---- 代入计算⑽11lim()1ln x x x x→--; 【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:11lim()1ln x x x x→--1ln (1)lim(1)ln x x x x x x →--=- ---- 通分化为商式,成为“00”未定型 1ln 11lim1ln x x x x x→+-=-+---- 应用洛必达法则1ln limln 1x x xx x x →=+- ---- 化简繁分式,成为“00”未定型 1ln 1limln 11x x x →+=++ ---- 应用洛必达法则 011022+==+ ---- 代入计算 ⑾tan 0lim xx x +→;【解】这是“00”幂指函数未定型极限,应化为商式极限后应用洛必达法则求解: 【解法一】应用对数法,令tan xy x=,则tan ln ln ln tan ln cot xxy xx x x===, 于是,00ln lim ln lim cot x x xy x ++→→= ---- 成为“∞∞”未定型021lim 1sin x x x+→=- ---- 应用洛必达法则20sin lim x x x +→= ---- 化简繁分式,成为“00”未定型 02sin cos lim 1x x x+→= ---- 应用洛必达法则2sin0cos00== ---- 代入计算得到 0l i m l n 0x y +→=,亦即0ln lim 0x y +→=, 从而有 0l i m 1x y e +→==,亦即tan 0lim 1xx x +→=。




导数结合洛必达法则巧解高考压轴题○2 洛必达法则可处理0 0, ,0 ,1 ,,0 , 型。
2010 年和 2011 年高考中的全国新课标卷中的第 21 题中的第 ○2 步,由不等式恒成立来求参数的0 0取值范围问题,分析难度大,但用洛必达法则来处理却可达到事半功倍的效果。
则不适用,应从另外途径求极限。
洛必达法则简介: ○4 若条件符合,洛必达法则可连续多次使用,直到求出极限为止。
法则 1 若函数 f(x) 和 g(x) 满足下列条件: (1) lim f x 0 及 lim g x 0;x a x a(2) a f(x) g(x) g'(x) 0 在点 的去心邻域内, 与 可导且 ≠ ;二.高考题处理1.(2010 年全国新课标理 )设函数x 2f (x) e 1 x ax 。
(3) limx af xg xl ,(1) 若a 0,求 f (x) 的单调区间; (2) 若当 x 0时 f (x) 0,求 a 的取值范围那么 limx af xg x= limx af xg xl 。
x x原解:(1) a 0时, ( ) 1f x e x , f '( x) e 1.法则 2 若函数 f(x) 和 g(x) 满足下列条件: (1) lim f x 0 及lim g x 0;x x当 x ( ,0) 时, f '( x) 0;当 x (0, ) 时, f '( x) 0 .故 f (x) 在( ,0) 单调减少,在(2) A f 0,f(x) 和 g(x) 在 ,A 与 A, 上可导,且 g'(x) ≠0;(0, ) 单调增加(3) limxf xg x l ,x(II ) '( ) 1 2f x e ax那么 limxf xg x=limxf xg xl。
x 由(I )知 1e x ,当且仅当 x 0时等号成立 .故f '( x) x 2ax (1 2a)x ,法则 3 若函数 f(x) 和 g(x) 满足下列条件: (1) limx af x 及 lim x ag x ;从而当 1 2a 0,即 1 a 时, f '( x) 0 ( x 0) ,而 f (0) 0 ,2(2) 在点 a 的去心邻域内, f(x) 与 g(x) 可导且 g'(x) ≠0;于是当 x 0时, f (x) 0 .(3) limx af xg xl ,x x由 e 1 x(x 0) 可得 e 1 x(x 0) .从而当1 a 时, 2那么 limf x= limx af xl 。




2.“洛必达法则”的有关定理,适用形式及计算定理(I ) 若函数()x f 与()x g 满足下列条件: (i )0lim ()0x x f x →=,0lim ()0x x g x →=;(ii )()f x 与()g x 在点0x 的某空心邻域内可导,且'()0g x ≠; (iii )0''()lim()x x f x A g x →=, 则0''()()limlim()()x x x x f x f x A g x g x →→==.定理(II ) 若函数()x f 与()x g 满足下列条件: (i )0lim ()x x f x →=∞,0lim ()x x g x →=∞;(ii )()f x 与()g x 在0x 点的某一邻域内可导,且'()0g x ≠; (iii )0''()lim()x x f x A g x →=, 则0''()()limlim()()x x x x f x f x A g x g x →→==.定理(I )和(II )可以接连应用几次,只要'()f x ,'()g x ,"()f x ,"()g x 等满足定理的条件即可。
除了00型和∞∞型未定式,还有∞∙0,∞-∞,1∞,00,∞0,等几种类型的未定式,这些未定式均可以化为00型或∞∞型未定式来计算。
1)0∞∙型未定式当0x x →或∞时,若()0f x →,()g x →∞,则()()()()x g x f x g x f 1≡∙或()()()()x f x g x g x f 1≡∙,这样,∞∙0型未定式就变为00型或∞∞型未定式。
2)∞-∞型未定式当0x x →或∞时,若()f x →∞,()g x →∞,则()()()()()()x g x f x g x f x g x f 1111∙-≡-这样,∞-∞型未定式就变为0型未定式。

(完整word版)导数结合洛必达法则巧解高考压轴题第一部分:历届导数高考压轴题(全国2理)设函数f (x) = (x+ 1)1 n( x + 1),若对所有的x>0,都有f (x) >ax成立,求实数a的取值范围.(辽宁理)设函数f(x)悝lnx In(x 1).1 x⑴求f(x)的单调区间和极值;(I)设a 0,讨论y f x的单调性;(U)若对任意x 0,1恒有f x 1,求a的取值范围. (全国1理)设函数f(x) e x e x.(I)证明:f(x)的导数f (x) > 2 ;(U)若对所有x > 0都有f (x) > ax,求a的取值范围.(新课标理)设函数f(x)=e x 1 x ax2.(I)若a 0,求f(x)的单调区间;(U)若当x>0时f(x) >0,求a的取值范围.导数结合洛必达法则巧解高考压轴题(I)求f(x)的单调区间;(全国1理)已知函数f x ax ⑵是否存在实数a ,使得关于x的不等式f (x)…a的解集为(0, 取值范围;若不存在,试说明理由.)?若存在,求a的(全国2理)设函数f(x)sin x2 cosx(新课标文)已知函数f(x) x(e x 1) ax2.(U)如果对任何x > 0,都有f(x) < ax,求a的取值范围.(I)若f(x)在x 1时有极值,求函数f(x)的解析式;例题:若不等式sin x x ax3对于x (0,三)恒成立,求a的取值范围(U)当x 0时,f(x) 0,求a的取值范围.(全国大纲理)设函数f (x) 1(I)证明:当x 1时,f(x)x 1(U)设当x 0时,f(x)—,求a的取值范围.ax 1第二部分:泰勒展开式(新课标理)已知函数f(x)霁x,曲线y f(x)在点(1,f(1))处的切线方程为x 2y 3 0.(I)求a、b的值;(U)如果当x 0,且x 1时,f(x)也k,求k的取值范围.x 1 x 1. e x 1 x1!x2!x3!K2 3x x2. ln(1 x) x2! 3!3 5x x3. sin x x ——K3! 5!2 4x x4. cosx 1 K2! 4!2 3(nxn!n 1xe(n 1)!nK ( 1)n1—n!2k 11)*,其中(0Rn,其中R nR n,其中R n1);n 11)n I^+)n1;2k 1k x(1) cos x ;(2 k 1)!2k 2(1)k4 Rn,其中R n2k(1)k話严x;1.(新课标理)已知函数f(x)b,曲线y f(x)在点(l,f(l))处的切线方x 1 x程为x 2y 3 0.(I)求a、b的值;(U)如果当x 0,且x 1时,f(x) 也k,求k的取值范围.x 1 x常规解法(I)略解得a 1,b 1.(n)方法一:分类讨论、假设反证法2 h(x) 0,与题设矛盾?综上可得,k的取值范围为(,0].1 x注:分三种情况讨论:① k 0 :②0 k 1 :③k 1不易想到.尤其是② 0 k 1时,许多考生都停留在此层面,举反例x (1,—1 )更难想到.而这方面根1 k据不同题型涉及的解法也不相同,这是高中阶段公认的难点,即便通过训练也很难提升.第三部分:洛必达法则及其解法洛必达法则:设函数f(x)、g(x)满足:(1)lim f(x) lim g(x) 0 ;x a x a(2)在U o(a)内,f (x)和g (x)都存在,且g (x) 0 ;(3)lim 3 A ( A可为实数,也可以是).x a g(x)则|im 他x m 3 A.x a g(x) x a g(x) 由(I)知f(x)—x 1,所以f (x) (罟-) 1 (2ln x(k 1)(x2丄)).x 1 x x 1 x 1 x x考虑函数h ;x) 2ln x(k1)(x2 1)(x 0),则h'(x)(k 1)(x221) 2xx x(i)当k 0时,由h'((x) k(x2 1) (x x2°知,当x1时,h'(x) 0.因为h(1) 0 ,所以当x (0,1)时,h(x) 0 ,可得」12 h(x) 0 ;x当x (1, )时,h(x)0,可得12 h(x)0,从而当x 0且x 1时,f(x) (ln:*) 0,即lnx f (x)k;1 x x 1 x x 1 x (ii )当0 k 1时,由于当X (1,1k)时,(k 1)(: x2 1) 2x 0,故h'(x) 0 ,而h(1)0 ,故当x (1, 1)时,h(x) 0,可得1 2 h(x) 0,与题设矛盾1 k 1 x(iii )当k 1时,h'(x) 0,而h(1)0,故当x (1, )时,h(x) 0 ,可得洛必达法则解法当x 0,且x也即k 则g '(x) xln xx 12(x21时,f(x)必兰,即x 1 x x 11 xln x 2x ln x亍1,记g(x)x x 1 1 x1)l nx 2(1 x2) 2(x21)“形= 羽(l nx(1 x2)2(1 x2)2ln x 1 ln x kx x 1 x3 1 , x 0,且x 11 x」)x2 1),t记h(x) In x2\2x )2 只,则h'(x)【儲= £+x2)从而h(x)在(0,)上单调递增,且h(1) 0,因此当(0,1)时,h(x) 0,当x (1,)时,h(x) 0 ;当x (0,1)时,g'(x) 0,当(1,)时,g'(x) 0 , 所以g(x)在(0,1)上单调递减,在(1,)上单调递增.由洛必达法则有xln x lim(-x 1 1 x1 时,g(x)l i m1g(x)即当xx l n x1) 1 lim r 1x 1 1 x20 ,即当x 0,且xIn xlimx 122x因为k g (x)恒成立, 所以k 0.综上所述, 成立, k的取值范围为(,0].1时,g(x) 0.0,且x 1 时,f(x)In x kx 1 x注:本题由已知很容易想到用分离变量的方法把参数出来的函数g(x)空与1求导,研究其单调性、极值1 x函数g(x)值没有意义”这一问题,很多考生会陷入困境k分离出来.然后对分离.此时遇到了“当x=1时, .如果考前对优秀的学生讲洛必达法则的应用,再通过强化训练就能掌握解决此类难题的这一有效方法2.(新课标理)设函数f (x) e x 1 x ax2.(I)若a 0,求f (x)的单调区间;(U)当x 0时,f(x) 0,求a的取值范围.应用洛必达法则和导数(U)当x 0 时,f(x) 0,即e x 1 x ax2.①当x记g(x)记h(x)h''(x)0时,axe 1 x2x(xxxe2)e xx (0,+0,所以h'(x)所以h(x) (x 2)e xx (0,+ )时,g'(x)由洛必达法则有,x女叫g(x)x叫一厂必XU XU x0时,e x 1 x ax2等价于),则g'(x) (x 2)e:x 2 x(0,+ ),则h'(x) (x 1)e x(x 1)e x 1在(0,+ )上单调递增,x 2在(0,+ )上单调递增,且h(x)0 ,从而g(x)xxe 1 x ,2 在(0,+xlimxxe 10 2xx..e 1limx 0 2 212综上所述,当a -且x2即当x 0 时,g(x) ,所以当x (0,+ )时,所以g(x)0时,f(x) 0成立.e x 1 x2 .x当x (0,+ )时,且h'(x) h'(0) 0 ,h(0) 0 ,因此当)上单调递增.1 1-,因此a丄.2 21故a 时,不等式sinx x ax 3对于x (0,—)恒成立.6 2例题:若不等式sinx x ax 3对于x (0,?)恒成立,求a 的取值范围.应用洛必达法则和导数当x (0,2)时,原不等式等价于ax sin x通过以上例题的分析,我们不难发现应用洛必达法则解决的试题应满足: ① 可以分离变量;② 用导数可以确定分离变量后一端新函数的单调性;③ 出现“ 0”型式子.x 3 x sinx 3sin x xcosx 2x 记 f(x) 3 ,则 f '(x) 4 . x x 记g(x) 3sinx xcosx 2x ,贝U g '(x) 2cosx xsinx 2 . 因为 g''(x) xcosx sinx cosx(x tanx), (海南宁夏文)已知函数 f (x) x(e x 1) ax 2.(I)若f (x)在x 1时有极值,求函数f (x)的解析式; (U)当x 0时,f(x) 0,求a 的取值范围.解: ( I)略(n)应用洛必达法则和导数g'''(x) xsi nx 0,所以g ''(x)在(0,?)上单调递减,且g''(x),所以g'(x)在(0-)上单调递减,且g'(x) 0.因此g(x)在(0-)上单调递减, 2 2 且g(x) 0,故f'(x) ?啤 0,因此f(x) x 严在(0_)上单调递减. x x 2 由洛必达法则有 li 叫 f(x)x sin x x 3 1 cosx sin x cosx lim 2 lim lim x 03x2 x 06x x 06①当x 0时, a R ;②当x 0时, x(e x 1)ax 2等价于e x x11 ax ,也即a.x记 g(x)xe 1, x (0,),则 g '(x) (x 1)e x 1xx记 h(x) (x 1)e x1 , x(0,),则h'(x) xe x 0,因此 h(x) (x 1)e x 1 在当 x 0 时,f(x) 0,即 x(e x 1) ax 2. 即当x 0时,g(x) 6,即有f(x)右(0,)上单调递增,且h(x)Xh(0) 0,所以 g'(x) 她 0,从而 g(x) -1在xx(0,)上单调递增. 由洛必达法则有(U)设当X 0时,f(x)—,求a的取值范围?ax 1解:(I)略(n)应用洛必达法则和导数由题设x 0,此时f (X) 0.①当a 0时,若x 1 a 则」0 ,ax 1 f(x) 不成立;ax 1②当a 0时,当X 0时,/ 、Xf(x) ,即1 X Xeax 1 ax 1 若x 0,则a R;若x 0,则1X eX X等价于1 e 1X X-,即 a Xe x e 1ax 1 x ax 1 xe X xxx, 2x2XcX, xxe e 1 e x e 2e 1 e z x 2 x、记g(x) x ,则g(x)x 2 = x 2(e x 2 e). xe x (xe x) (xe x)(I)求f(x)的单调区间;(n)如果对任何x > 0,都有f(x) < ax,求a的取值范围.(2 cosx)cos x sin x( sin x) 2cosx 1 解:(I) f(x) -) yco^2 n 2 n当2k n E x 2k n孑(k Z)时,cosxX叫g(x)X lim —x 0 x即当X 0时,g(x) 1 记h(x) e x x2 2 e x,则h'(x) e x 2x e x,h''(x) e x+e x 2 0.因此,h'(x) e x 2x e x在(0,)上单调递增,且h'(0) 0,所以h'(x) 0,所以g(X) 1,即有a 1.综上所述,当a 1 , X 0时,f (X) 0成立. 因此g'(x)=Xex 2(xe x)h(x) 0,所以g(x)在(0,)上单调递增.(全国大纲理) 设函数f (x) 1 (I)证明:当X 1 时,f(x) 由洛必达法则有X叫g(x)g(x)X Xxe elim x——x 0 xe xXxelim x x x 0 exeXxeXxe0时, i,即有g(x) 2,所以a i.综上所述,a的取值范围是((全国2理)设函数f(x)sin x2 cosx12,即f(X) 0;2 n当 2k n x4n (k Z )时,cosx1—,即 f (x)332因此f(x)在每- 」个区间 2k nNfk n2 n(kZ )是增函数,33f(x)在每一个区间 2k n2 n3 4 n ,2k n 3(k Z ) 是减函数.另一方面,当x [,)时,g(x )xj ;:sx )2 J 2,因此a 右解:(I)略(n)应用洛必达法则和导数sin x ax 2 cosx 0,则 a R ;2xcosx 2sin x sin xcosx x 则 g '(x)-------------------------- x ^厂o 击 ----------记 h(x) 2xcosx 2sinx sin xcosx x , h'(x) 2cosx 2xsinx 2cosx cos2x 122xsinx cos2x 1 2sin x 2xsinx 2sin x(sinx x)因此,当x (0,)时,h'(x) O,h(x)在(0,)上单调递减,且h(0)0,故g'(x) 0,所以g(x)在(0, )上单调递减,而 lim g(x) x 0 limx 0 sin x x(2 cosx) lim cosxx 02+cosx xsinxf(x)若x若x 0,贝U sin x ax 等价于a2 cosxsin x x(2 cosx)即 g(x)sin x x(2 cosx)。

洛必达法则若0)(lim =→x f ax ,0)(lim =→x g ax ,则 )()(limx g x f ax → 称为00的待定型。
类似的待定型有:00,∞∞,∞⋅0,∞-∞,∞1,00,0∞。
xx x sin lim0→,x xx ln lim +∞→,x x x ln lim 0+→,)11(lim 22--+∞→x x x , xx x 1)1(lim +→,x x x )(sin lim 0→,下面的洛必达(L 'hospital ,1661一1704)法则,有助于我们求解这类待定型的极限. 定理5.6 若(1) ()f x ,()g x 在(,)a a δ+可导且()g x '0≠,其中0δ>; (2) lim x a+→()f x =lim x a+→()g x =0;(3) lim x a +→()()f xg x ''=A ,则 ()lim ()x a f x A g x +→=. 证明 补充定义()f a =()g a =0,则当x ∈(,)a a δ+时,用柯西中值定理()()f x g x =()()()()f x f a g x g a --=()()f g ξξ'',a x ξ<<.当+→a x 时,a ξ+→,故 ()lim ()x af x Ag x +→= 定理5.6证完。
定理5.7 若(1) ()f x ,()g x 在(,)a +∞可导,且()g x '0≠,其中a 是某个实数; (2) lim x →+∞()f x =lim x →+∞()g x =0;(3) limx →+∞()()f xg x ''=A , )()(lim )()(lim x g x f x g x f a x a x ''=++→→在直观上是不难理解的:两个无穷小量的比等于它们变化速度的比.注1 极限A 可以是有限数,也可以是∞或∞±,结论仍成立。
1.用洛必达法则求下列极限:⑴0sin limsin x axbx→;【解】这是“00”未定型商式极限,可以应用洛必达法则求解:0sin lim sin x ax bx →0cos limcos x a axb bx→= ---- 应用洛必达法则 cos 0cos 0a b =11a b ⨯=⨯ab=。
---- 代值计算 ⑵30sin lim x x x x→-; 【解】这是“00”未定型商式极限,可以应用洛必达法则求解:30sin lim x x x x →-201cos lim 3x x x →-= ---- 应用洛必达法则 0sin lim 6x x x→= ---- 对未定型商式再应用洛必达法则116=⨯ ---- 套用极限公式 ()0sin ()lim1()f x f x f x →=16=⑶332132lim 1x x x x x x →-+--+;【解】这是“0”未定型商式极限,可以应用洛必达法则求解:332132lim 1x x x x x x →-+--+22133lim 321x x x x →-=-- ---- 应用洛必达法则 16lim62x xx →=- ---- 对未定型商式再应用洛必达法则63622==- ---- 代值计算 ⑷2tan limtan 3x xxπ→;【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2tan lim tan 3x x x π→2221cos lim 3cos 3x x xπ→= ---- 应用洛必达法则 222cos 3lim3cos x xx π→= ---- 整理繁分式 22cos3(sin 3)3lim32cos (sin )x x x x x π→⋅-⋅=⋅⋅- ---- 对未定型商式再应用洛必达法则2sin 6limsin 2x xxπ→= ---- 化简复杂分式 26cos6lim2cos 2x xxπ→= ---- 对未定型商式再应用洛必达法则3cos3cos ππ=---- 代值计算3=⑸2lim x ; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解:2limx12ln lim 1x x x →+∞⋅= ---- 应用洛必达法则limx = ---- 化简繁分式14lim 1x x →+∞= ---- 对未定型商式再应用洛必达法则limx →+∞= ---- 化简繁分式 0=⑹2ln()2lim tan x x x ππ+→-; 【解】这是“∞∞”未定型商式极限,可以应用洛必达法则求解: 2ln()2lim tan x x x ππ+→-2212lim 1cos x x xππ+→-= ---- 应用洛必达法则 22cos lim 2x x x ππ+→=----- 化简繁分式22cos (sin )lim 1x x x π+→-= ---- 对未定型商式再应用洛必达法则2cossin22ππ=-0= ---- 代入计算⑺2120lim x x x e →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:212lim xx x e →2102lim 1x x e x→= ---- 化为商式后,成为“∞∞”未定型商式极限212021()'lim 1()'x x e x x→= ---- 应用洛必达法则2211lim x x e →+∞= ---- 化简繁分式 =+∞ ---- 代入计算⑻0lim cot x x x →;【解】这是“0⨯∞”未定型极限,应化为商式极限后应用洛必达法则求解:lim cot x x x →0limtan x xx →= ---- 化为商式后,成为“∞∞”未定型商式极限21lim1cos x x→= ---- 应用洛必达法则 20limcos x x →= ---- 化简繁分式2cos 01== ---- 代入计算⑼2lim(sec tan )x x x π→-;【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:2lim(sec tan )x x x π→-21sin lim()cos cos x x x xπ→=- ---- 为通分化为商式作准备21sin limcos x xx π→-= ---- 成为“00”未定型商式极限2cos limsin x xxπ→-=- ---- 应用洛必达法则cos 20sin2ππ== ---- 代入计算⑽11lim()1ln x x x x→--; 【解】这是“∞-∞”未定型极限,应化为商式极限后应用洛必达法则求解:11lim()1ln x x x x→--1ln (1)lim(1)ln x x x x x x →--=- ---- 通分化为商式,成为“00”未定型1ln 11lim1ln x x x x x →+-=-+---- 应用洛必达法则1ln limln 1x x xx x x →=+- ---- 化简繁分式,成为“00”未定型1ln 1limln 11x x x →+=++ ---- 应用洛必达法则011022+==+ ---- 代入计算 ⑾tan 0lim x x x +→;【解】这是“00”幂指函数未定型极限,应化为商式极限后应用洛必达法则求解:【解法一】应用对数法,令tan x y x =,则tan ln ln ln tan ln cot x xy x x x x===, 于是,00ln lim ln limcot x x xy x ++→→= ---- 成为“∞∞”未定型021lim 1sin x x x +→=- ---- 应用洛必达法则 20sin lim x x x +→= ---- 化简繁分式,成为“00”未定型2sin cos lim 1x x x+→= ---- 应用洛必达法则2sin0cos00== ---- 代入计算得到 0lim ln 0x y +→=,亦即0ln lim 0x y +→=,从而有 00lim 1x y e +→==,亦即tan 0lim 1x x x +→=。
第十七讲Ⅰ 授课题目:§3.2 洛必塔法则 Ⅱ 教学目的与要求:1.掌握用罗必塔法则求极限;2.明了使用罗必塔法则的条件;3.了解将罗必塔法则与极限运算性质结合使用常能简化运算。
Ⅲ 教学重点与难点:重点:各种类型的未定式转化为00或∞∞型的未定式 难点:罗必塔法则与极限运算性质的结合使用 Ⅳ 讲授内容:§3.2 洛必塔法则如果当a x →(或∞→x )时,两个函数)(x f 与)(x F 都趋于零或都趋于无穷大,那末极限)()(lim)(x F x f x a x ∞→→可能存在、也可能不存在.通常把这种极限叫做未定式,并分别简记为00或∞∞.在第一章第六节中讨论过的极限x x x sin lim 0→就是未定式00的一个例子.对于这类极限,即使它存在也不能用“商的极限等于极限的商”这—法则.下面我们将根据柯西中值定理来推出求这类极限的一种简便且重要的方法. 我们着重讨论a x →时的未定式的情形,关于这情形有以下定理: 定理1 设 (1)当a x →时,函数)(x f 及)(x F 都趋于零;(2)在点a 的某去心邻域内,)(x f '及)(x F '都存在且0)(≠'x F ; (3))()(limx F x f ax ''→存在(或为无穷大), 那么 )()(lim )()(limx F x f x F x f a x ax ''=→→. 这就是说,当)()(lim x F x f ax ''→存在时,)()(lim x F x f a x →也存在且等于)()(lim x F x f a x ''→;当)()(lim x F x f a x ''→为无穷大时,)()(limx F x f ax →也是无穷大.这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必塔(L ’Hospital )法则 证明 因为求)()(x F x f 当a x →时的极限与)(a f 及)(a F 无关,所以可以假定0)()(==a F a f ,于是由条件(1)、(2)知道,)(x f 及)(x F 在点a 的某一邻域内是连续的.设x 是这邻域内的一点,那么在以x 及a 为端点的区间上,柯西中值定理的条件均满足,因此有)()()()()()()()(ξξF f a F x F a f x f x F x f ''=--= (ξ在x 与a 之间). 令a x →,并对上式两端求极限,注意到a x →时a →ξ,再根据条件(3)便得说明: 1.如果)()(limx F x f a x ''→仍属于00型, 且)(x f '和)(x F '满足洛必达法则的条件,可继续使用洛必达法则, 即 =''''=''=→→→)()(lim )()(lim )()(limx F x f x F x f x F x f a x a x a x ;2.当∞→x 时, 该法则仍然成立, 有)()(lim )()(lim x F x f x F x f x x ''=∞→∞→;3.对a x →(或∞→x )时的未定式∞∞,也有相应的洛必达法则;4. 洛必达法则是充分条件,反之不成立;5. 如果数列极限也属于未定式的极限问题,需先将其转换为函数极限,然后使用洛必达法则,从而求出数列极限.(因为数列不连续,不能求导) 例1 求下列极限(1)x xx tan lim 0→, (00型) (2)123lim 2331+--+-→x x x x x x , (00型) 解 原式=)()(tan lim 0''→x x x =11sec lim 20=→x x 原式= 12333lim 221---→x x x x = =-→266lim 1x x x 23注 上式中的266lim1-→x xx 已不是未定式,不能对它应用洛必达法则,否则要导致错误结果.以后使用洛必达法则时应当经常注意这一点,如果不是未定式,就不能应用洛必达法则.(3)xx x 1arctan 2lim -+∞→π, (00型) 原式=22111limxx x -+-+∞→=221lim x x x ++∞→=1 (4)bx ax x sin ln sin ln lim0→, (∞∞型). 原式= ax bx b bx ax a x sin cos sin cos lim0⋅⋅→= ax bx x cos cos lim 0→=1(5)xx x 3tan tan lim 2π→, (∞∞型) 原式=x x x 3sec 3sec lim 222π→= x x x 222cos 3cos lim 31π→= x x x x x sin cos 23sin 3cos 6lim 312--→π= x x x 2sin 6sin lim 2π→= 32cos 26cos 6lim 2=→x xx π注意:洛必达法则是求未定式的一种有效方法,但与其它求极限方法结合使用,效果更好.例2 求下列极限(1)x x xx x tan tan lim 20-→ 原式30tan lim x x x x→-== 22031sec lim x x x -→=220tan lim 31x x x →=31 (2)0ln lim ln(1)x x x e +→- 原式0001111lim lim lim 11x x x x x x x x e x x e x e x ee +++→→→-==⋅=⋅=- (3)1ln cos(1)lim 1sin 2x x xπ→-- 原式2111sin(1)2sin(1)4cos(1)cos(1)lim lim lim cos cos sin 2222x x x x x x x x x x ππππππ→→→-----===--24π=-练习:(1)30arcsin lim sin x x xx→- (2)20ln(1)lim sec cos x x x x →+- 二.0,1,0,,0∞∞-∞∞⋅∞型未定式的求法关键: 将其它类型未定式化为洛必达法则可解决的类型00型和∞∞型.1.∞⋅0型未定式的求法 步骤:,10∞⋅∞⇒∞⋅或0100⋅⇒∞⋅ 例3 求下列极限(1).lim 2xx e x -+∞→ 原式=2lim x e x x +∞→=x e x x 2lim +∞→2lim xx e +∞→=.+∞=(2)0lim cot x x x → 原式20011limlim tan 22sec 2x x x x x →→===型∞-∞.2步骤:0101-⇒∞-∞.0000⋅-⇒ 例4 求下列极限 (1)).1sin 1(lim 0x x x -→ 原式=xx x x x sin sin lim 0⋅-→x x x x x cos sin cos 1lim 0+-=→.0=(2)011lim ln(1)x x x →⎡⎤-⎢⎥+⎣⎦原式200011ln(1)ln(1)1lim lim lim ln(1)2x x x x x x x x x x x x→→→--+-++===+ 011lim2(1)2x x →==+型00,1,0.3∞∞步骤: ⎪⎩⎪⎨⎧∞⋅⋅∞⋅−−→−⎪⎭⎪⎬⎫∞∞ln 01ln 0ln 01000取对数.0∞⋅⇒例3 求下列极限(1).lim 0xx x +→ 原式=xx x eln 0lim +→xx x eln lim 0+→=xxx e 1ln lim 0+→=2011lim xxx e-+→=0e =.1=(2)11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭原式0lnsin ln 1lim1cos 3...x x x xee →---===例4 求下列极限(1).lim111xx x-→ 原式=x xx eln 111lim -→xx x e-→=1ln lim111lim 1-→=x x e .1-=e(2)10lim(1sin )xx x →+ 原式00cos ln(1sin )1sin lim lim 1x x xx x xeee →→++===例5 求下列极限(1).)(cot lim ln 10xx x +→ 原式20011ln(cot )cot sin limlim1ln 1/x x x x x x xe ee ++→→-⋅-===(2)()1lim ln xx x →+∞原式11ln(ln )ln lim lim 011x x x x x xeee →+∞→+∞⋅====例6 求)]24([tan lim nnn +→∞π解 设)]24([tan )(x x f x +=π,则)]24([tan )(nn f n +=π 因为)]24tan(ln lim exp[)(lim xx x f x x +=+∞→+∞→π=]1)24tan(ln limexp[x x x ++∞→π])24tan(1)2)(24(sec lim exp[222x xx x x +--+=+∞→ππ=4e 从而 原式=4)(lim )(lim e x f n f x n ==+∞→∞→练习:1))1(cot lim 0xx x -→ (2)x x x ln 10)(cot lim +→ (3)xx x tan 0lim +→(4)xx x 2tan 4)(tan lim π→(5)xx x cot 0)sin 1(lim -→Ⅴ 小结与提问:小结:1.使用罗必塔法则之前应该验明其是否满足罗必塔法则条件。
2.罗必塔法则是求未定型极限的有效方法,但不是万能的。
提问:求极限xx xx x cos 23sin 3lim -+∞→时能否使用罗必塔法则?Ⅵ 课外作业:137P 1. (6) (7) (9) (12) (16) 4.(注:本资料素材和资料部分来自网络,仅供参考。
请预览后才下载,期待您的好评与关注!)。