最优化方法之 对偶理论讲解
- 格式:ppt
- 大小:1.23 MB
- 文档页数:59






优化问题中的对偶理论在数学中,优化问题是一种求解最优解的问题,而对偶理论则是用来解决优化问题中的复杂性的一种方法。
对偶理论的核心思想是将原问题转化为它的对偶问题,并在对偶问题中求解最优解。
本文将介绍优化问题中的对偶理论及其应用。
1. 对偶问题的定义对偶问题是指将一个优化问题转化为另一个优化问题的过程。
具体来说,对于一个原始问题(称为Primal Problem),我们可以通过构造一个对应的对偶问题(称为Dual Problem),来找到原始问题的最优解。
这个对应关系是双向的,即可以从原始问题得到对偶问题,也可以从对偶问题得到原始问题。
对于一个具体的优化问题,我们可以定义它的原始问题和对偶问题。
原始问题通常形式如下:Minimize f(x)subject to g_i(x) ≤ 0, i = 1, 2, ..., mh_j(x) = 0, j = 1, 2, ..., n其中,f(x)是目标函数,g_i(x)是不等式约束,h_j(x)是等式约束。
而对偶问题的形式如下:Maximize g(λ, μ)subject to λ_i ≥ 0, i = 1, 2, ..., m其中,g(λ, μ)是对偶函数,λ_i和μ_j分别是对应原始问题中不等式约束和等式约束的Lagrange乘子。
2. 对偶问题的求解对于一个原始问题,我们可以通过下列步骤求解它的对偶问题:1)构造对偶函数:对偶函数是原始问题的Lagrange对偶,它定义为:g(λ, μ) = inf{ f(x) + ∑ λ_i g_i(x) + ∑ μ_j h_j(x) }其中,inf{}表示检查所有可行解的最小值。
2)求对偶问题:将对偶函数最大化,得到对偶问题的最优解。
3)寻找最优解:将对偶问题的最优解带回到原始问题中,可以获得原始问题的最优解。
这个过程可能看起来很抽象和复杂,但对偶理论的优点在于它可以将复杂的原始问题转化为相对简单的对偶问题,从而更容易求解。


对偶理论知识点总结一、一般理解对偶理论是运筹学和数学中的一个重要理论,主要研究优化问题的对偶性质和利用对偶问题来解决原始问题的方法。
优化问题是现实世界中的一种普遍问题,它的目标是在一定的约束条件下找到最优解。
而对偶理论则是研究优化问题的一个重要角度,它告诉我们,对于每一个原始问题都存在一个对偶问题,通过对偶问题我们可以获得原始问题的一些重要信息,比如最优解的下界。
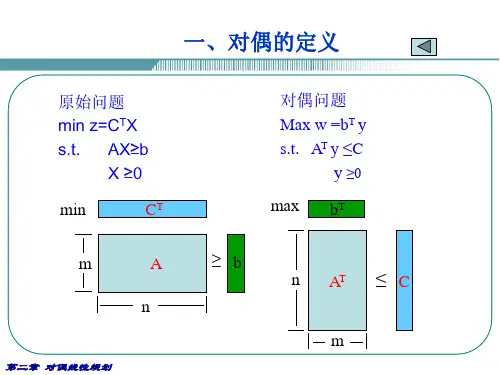
二、对偶问题的定义在深入了解对偶理论之前,我们首先需要了解什么是对偶问题。
对于一个原始优化问题:\[ \begin{cases} inf \ c^T x \\ Ax=b \\ x\geq0 \end{cases}\]它的对偶问题可以定义为:\[ \begin{cases} sup \ b^T y \\ A^Ty+c=y \\ y\geq0 \end{cases}\]其中,\(c,x\)是原始问题的目标函数和解向量,\(A,b\)是原始问题的约束条件,对偶问题的目标函数和解向量分别为\(b,y\)。
原始问题和对偶问题之间存在着一种对偶关系,通过对偶问题我们可以获得原始问题的一些重要信息。
三、对偶性质对偶理论的一个重要性质就是对偶性质,它告诉我们原始问题和对偶问题之间存在着一种非常紧密的联系。
具体来讲,对偶性质包括弱对偶性和强对偶性两个方面。
1. 弱对偶性:对于任意一个优化问题,其对偶问题的目标函数值不会超过原始问题的目标函数值,即对于原始问题的任意可行解x和对偶问题的任意可行解y,有\[c^Tx\geqb^Ty\]2. 强对偶性:若原始问题和对偶问题均存在最优解,则它们的目标函数值相等,即\[inf \c^Tx=sup \ b^Ty\]这两个对偶性质告诉我们,对偶问题的解可以为原始问题的最优解提供一个下界,并且在某些情况下,对偶问题的解可以等于原始问题的最优解。
四、对偶问题的应用对偶理论不仅仅是一种理论概念,更是一种实际问题求解的工具。
在实际问题中,我们经常可以通过对偶问题来求解原始问题,或者通过对偶问题的解来获得原始问题的解。


对偶优化方法
对偶优化方法是一种处理优化问题的方法,它将原始问题转化为对偶问题,以简化求解过程。
以下是关于对偶优化方法的一些关键点:
1. 对偶问题的定义:对于给定的优化问题,其原始问题是寻找一个最优解,使得某些目标函数达到最小值。
而对偶问题则是寻找一个最优解,使得一些约束条件下的某些目标函数达到最大值。
2. 对偶优化方法的特点:对偶优化方法的主要特点在于其对原始问题的转化。
通过对偶变换,可以将复杂的问题转化为相对简单的问题,从而更容易找到最优解。
此外,对偶优化方法还可以利用一些特殊的性质,如对偶性、互补性等,来简化计算过程。
3. 对偶优化方法的应用:对偶优化方法在许多领域都有广泛的应用,如机器学习、信号处理、网络优化等。
例如,在机器学习中,一些算法(如支持向量机、梯度下降法等)可以通过对偶优化方法进行求解。
4. 对偶优化方法的局限:虽然对偶优化方法具有许多优点,但也有其局限性。
例如,对于一些非线性、非凸的问题,对偶优化方法可能无法找到全局最优解。
此外,对偶优化方法也可能涉及到大规模的计算,需要高效的算法和计算资源才能实现。
总之,对偶优化方法是一种重要的优化技术,它可以有效地解决许多复杂的问题。
然而,在使用对偶优化方法时,需要注意其局限性和适用范围,以便更好地应用该方法。