三角函数1234567

三角函数公式大全一、定义锐角三角函数任意角三角函数图形直正弦（sin）余弦（cos）正切（tan或tg）余切（cot或ctg）正割（sec）余割（csc）二、函数关系倒数关系：；；商数关系：；．平方关系：；；三、诱导公式口诀：奇变偶不变，符号看象限公式一：设为任意角，终边相同的角的同一三角函数的值相等：公式二：设为任意角，与的三角函数值之间的关系：公式三：任意角与的三角函数值之间的关系：公式四：与的三角函数值之间的关系：公式五：与的三角函数值之间的关系：公式六：及与的三角函数值之间的关系：四、基本公式1.和差角公式口诀：正余同余正，余余反正正；；；2.和差化积口诀：正加正，正在前。

正减正，余在前。

余加余，余并肩。

余减余，余不见，负号很讨厌。

；；3.积化和差4.倍角公式sin4A=-4*(cosA*sinA*（2*sinA^2-1））cos4A=1+(-8*cosA^2+8*cosA^4）tan4A=（4*tanA-4*tanA^3）/（1-6*tanA^2+tanA^4）5.半角公式五、万能公式六、辅助角公式七、三角形定理1.正弦定理在任意△ABC中，角A、B、C所对的边长分别为a、b、c，三角形外接圆的半径为R．则有正弦定理变形可得：2.余弦定理在如图所示的在△ABC中，有或（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。

可复制、编制，期待你的好评与关注）。

【数学知识点】特殊三角函数值顺口溜1、三十，四五，六十度，三角函数记牢固；分母弦二切是三，分子要把根号添；一二三来三二一，切值三九二十七；递增正切和正弦，余弦函数要递减。

2、三角函数是函数，象限符号坐标注。

函数图象单位圆，周期奇偶增减现。

同角关系很重要，化简证明都需要。

正六边形顶点处，从上到下弦切割。

三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

也可以等价地用与单位圆有关的各种线段的长度来定义。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

常见的三角函数包括正弦函数、余弦函数和正切函数。

在航海学、测绘学、工程学等其他学科中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。

不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

三角函数一般用于计算三角形中未知长度的边和未知的角度，在导航、工程学以及物理学方面都有广泛的用途。

另外，以三角函数为模版，可以定义一类相似的函数，叫做双曲函数。

常见的双曲函数也被称为双曲正弦函数、双曲余弦函数等等。

三角函数（也叫做圆函数）是角的函数；它们在研究三角形和建模周期现象和许多其他应用中是很重要的。

三角函数通常定义为包含这个角的直角三角形的两个边的比率，也可以等价的定义为单位圆上的各种线段的长度。

更现代的定义把它们表达为无穷级数或特定微分方程的解，允许它们扩展到任意正数和负数值，甚至是复数值。

感谢您的阅读，祝您生活愉快。

三角函数0~360°表sin(0°)=0.000000,cos(0°)=1.000000,tan(0°)=0.000000 sin(1°)=0.017452,cos(1°)=0.999848,tan(1°)=0.017455 sin(2°)=0.034899,cos(2°)=0.999391,tan(2°)=0.034921 sin(3°)=0.052336,cos(3°)=0.998630,tan(3°)=0.052408 sin(4°)=0.069756,cos(4°)=0.997564,tan(4°)=0.069927 sin(5°)=0.087156,cos(5°)=0.996195,tan(5°)=0.087489 sin(6°)=0.104528,cos(6°)=0.994522,tan(6°)=0.105104 sin(7°)=0.121869,cos(7°)=0.992546,tan(7°)=0.122785 sin(8°)=0.139173,cos(8°)=0.990268,tan(8°)=0.140541 sin(9°)=0.156434,cos(9°)=0.987688,tan(9°)=0.158384 sin(10°)=0.173648,cos(10°)=0.984808,tan(10°)=0.176327 sin(11°)=0.190809,cos(11°)=0.981627,tan(11°)=0.194380 sin(12°)=0.207912,cos(12°)=0.978148,tan(12°)=0.212557 sin(13°)=0.224951,cos(13°)=0.974370,tan(13°)=0.230868 sin(14°)=0.241922,cos(14°)=0.970296,tan(14°)=0.249328 sin(15°)=0.258819,cos(15°)=0.965926,tan(15°)=0.267949 sin(16°)=0.275637,cos(16°)=0.961262,tan(16°)=0.286745 sin(17°)=0.292372,cos(17°)=0.956305,tan(17°)=0.305731 sin(18°)=0.309017,cos(18°)=0.951057,tan(18°)=0.324920 sin(19°)=0.325568,cos(19°)=0.945519,tan(19°)=0.344328 sin(20°)=0.342020,cos(20°)=0.939693,tan(20°)=0.363970 sin(21°)=0.358368,cos(21°)=0.933580,tan(21°)=0.383864 sin(22°)=0.374607,cos(22°)=0.927184,tan(22°)=0.404026 sin(23°)=0.390731,cos(23°)=0.920505,tan(23°)=0.424475 sin(24°)=0.406737,cos(24°)=0.913545,tan(24°)=0.445229 sin(25°)=0.422618,cos(25°)=0.906308,tan(25°)=0.466308 sin(26°)=0.438371,cos(26°)=0.898794,tan(26°)=0.487733sin(27°)=0.453990,cos(27°)=0.891007,tan(27°)=0.509525 sin(28°)=0.469472,cos(28°)=0.882948,tan(28°)=0.531709 sin(29°)=0.484810,cos(29°)=0.874620,tan(29°)=0.554309 sin(30°)=0.500000,cos(30°)=0.866025,tan(30°)=0.577350 sin(31°)=0.515038,cos(31°)=0.857167,tan(31°)=0.600861 sin(32°)=0.529919,cos(32°)=0.848048,tan(32°)=0.624869 sin(33°)=0.544639,cos(33°)=0.838671,tan(33°)=0.649408 sin(34°)=0.559193,cos(34°)=0.829038,tan(34°)=0.674509 sin(35°)=0.573576,cos(35°)=0.819152,tan(35°)=0.700208 sin(36°)=0.587785,cos(36°)=0.809017,tan(36°)=0.726543 sin(37°)=0.601815,cos(37°)=0.798636,tan(37°)=0.753554 sin(38°)=0.615661,cos(38°)=0.788011,tan(38°)=0.781286 sin(39°)=0.629320,cos(39°)=0.777146,tan(39°)=0.809784 sin(40°)=0.642788,cos(40°)=0.766044,tan(40°)=0.839100 sin(41°)=0.656059,cos(41°)=0.754710,tan(41°)=0.869287 sin(42°)=0.669131,cos(42°)=0.743145,tan(42°)=0.900404 sin(43°)=0.681998,cos(43°)=0.731354,tan(43°)=0.932515 sin(44°)=0.694658,cos(44°)=0.719340,tan(44°)=0.965689 sin(45°)=0.707107,cos(45°)=0.707107,tan(45°)=1.000000 sin(46°)=0.719340,cos(46°)=0.694658,tan(46°)=1.035530 sin(47°)=0.731354,cos(47°)=0.681998,tan(47°)=1.072369 sin(48°)=0.743145,cos(48°)=0.669131,tan(48°)=1.110613 sin(49°)=0.754710,cos(49°)=0.656059,tan(49°)=1.150368 sin(50°)=0.766044,cos(50°)=0.642788,tan(50°)=1.191754 sin(51°)=0.777146,cos(51°)=0.629320,tan(51°)=1.234897 sin(52°)=0.788011,cos(52°)=0.615661,tan(52°)=1.279942 sin(53°)=0.798636,cos(53°)=0.601815,tan(53°)=1.327045 sin(54°)=0.809017,cos(54°)=0.587785,tan(54°)=1.376382 sin(55°)=0.819152,cos(55°)=0.573576,tan(55°)=1.428148 sin(56°)=0.829038,cos(56°)=0.559193,tan(56°)=1.482561sin(57°)=0.838671,cos(57°)=0.544639,tan(57°)=1.539865 sin(58°)=0.848048,cos(58°)=0.529919,tan(58°)=1.600335 sin(59°)=0.857167,cos(59°)=0.515038,tan(59°)=1.664279 sin(60°)=0.866025,cos(60°)=0.500000,tan(60°)=1.732051 sin(61°)=0.874620,cos(61°)=0.484810,tan(61°)=1.804048 sin(62°)=0.882948,cos(62°)=0.469472,tan(62°)=1.880726 sin(63°)=0.891007,cos(63°)=0.453990,tan(63°)=1.962611 sin(64°)=0.898794,cos(64°)=0.438371,tan(64°)=2.050304 sin(65°)=0.906308,cos(65°)=0.422618,tan(65°)=2.144507 sin(66°)=0.913545,cos(66°)=0.406737,tan(66°)=2.246037 sin(67°)=0.920505,cos(67°)=0.390731,tan(67°)=2.355852 sin(68°)=0.927184,cos(68°)=0.374607,tan(68°)=2.475087 sin(69°)=0.933580,cos(69°)=0.358368,tan(69°)=2.605089 sin(70°)=0.939693,cos(70°)=0.342020,tan(70°)=2.747477 sin(71°)=0.945519,cos(71°)=0.325568,tan(71°)=2.904211 sin(72°)=0.951057,cos(72°)=0.309017,tan(72°)=3.077684 sin(73°)=0.956305,cos(73°)=0.292372,tan(73°)=3.270853 sin(74°)=0.961262,cos(74°)=0.275637,tan(74°)=3.487414 sin(75°)=0.965926,cos(75°)=0.258819,tan(75°)=3.732051 sin(76°)=0.970296,cos(76°)=0.241922,tan(76°)=4.010781 sin(77°)=0.974370,cos(77°)=0.224951,tan(77°)=4.331476 sin(78°)=0.978148,cos(78°)=0.207912,tan(78°)=4.704630 sin(79°)=0.981627,cos(79°)=0.190809,tan(79°)=5.144554 sin(80°)=0.984808,cos(80°)=0.173648,tan(80°)=5.671282 sin(81°)=0.987688,cos(81°)=0.156434,tan(81°)=6.313752 sin(82°)=0.990268,cos(82°)=0.139173,tan(82°)=7.115370 sin(83°)=0.992546,cos(83°)=0.121869,tan(83°)=8.144346 sin(84°)=0.994522,cos(84°)=0.104528,tan(84°)=9.514364 sin(85°)=0.996195,cos(85°)=0.087156,tan(85°)=11.430052 sin(86°)=0.997564,cos(86°)=0.069756,tan(86°)=14.300666sin(87°)=0.998630,cos(87°)=0.052336,tan(87°)=19.081137sin(88°)=0.999391,cos(88°)=0.034899,tan(88°)=28.636253sin(89°)=0.999848,cos(89°)=0.017452,tan(89°)=57.289962sin(90°)=1.000000,cos(90°)=0.000000,tan(90°)=无意义sin(91°)=0.999848,cos(91°)=-0.017452,tan(91°)=-57.289962 sin(92°)=0.999391,cos(92°)=-0.034899,tan(92°)=-28.636253 sin(93°)=0.998630,cos(93°)=-0.052336,tan(93°)=-19.081137 sin(94°)=0.997564,cos(94°)=-0.069756,tan(94°)=-14.300666 sin(95°)=0.996195,cos(95°)=-0.087156,tan(95°)=-11.430052 sin(96°)=0.994522,cos(96°)=-0.104528,tan(96°)=-9.514364 sin(97°)=0.992546,cos(97°)=-0.121869,tan(97°)=-8.144346 sin(98°)=0.990268,cos(98°)=-0.139173,tan(98°)=-7.115370 sin(99°)=0.987688,cos(99°)=-0.156434,tan(99°)=-6.313752 sin(100°)=0.984808,cos(100°)=-0.173648,tan(100°)=-5.671282 sin(101°)=0.981627,cos(101°)=-0.190809,tan(101°)=-5.144554 sin(102°)=0.978148,cos(102°)=-0.207912,tan(102°)=-4.704630 sin(103°)=0.974370,cos(103°)=-0.224951,tan(103°)=-4.331476 sin(104°)=0.970296,cos(104°)=-0.241922,tan(104°)=-4.010781 sin(105°)=0.965926,cos(105°)=-0.258819,tan(105°)=-3.732051 sin(106°)=0.961262,cos(106°)=-0.275637,tan(106°)=-3.487414 sin(107°)=0.956305,cos(107°)=-0.292372,tan(107°)=-3.270853 sin(108°)=0.951057,cos(108°)=-0.309017,tan(108°)=-3.077684 sin(109°)=0.945519,cos(109°)=-0.325568,tan(109°)=-2.904211 sin(110°)=0.939693,cos(110°)=-0.342020,tan(110°)=-2.747477 sin(111°)=0.933580,cos(111°)=-0.358368,tan(111°)=-2.605089 sin(112°)=0.927184,cos(112°)=-0.374607,tan(112°)=-2.475087 sin(113°)=0.920505,cos(113°)=-0.390731,tan(113°)=-2.355852 sin(114°)=0.913545,cos(114°)=-0.406737,tan(114°)=-2.246037 sin(115°)=0.906308,cos(115°)=-0.422618,tan(115°)=-2.144507 sin(116°)=0.898794,cos(116°)=-0.438371,tan(116°)=-2.050304sin(117°)=0.891007,cos(117°)=-0.453990,tan(117°)=-1.962611 sin(118°)=0.882948,cos(118°)=-0.469472,tan(118°)=-1.880726 sin(119°)=0.874620,cos(119°)=-0.484810,tan(119°)=-1.804048 sin(120°)=0.866025,cos(120°)=-0.500000,tan(120°)=-1.732051 sin(121°)=0.857167,cos(121°)=-0.515038,tan(121°)=-1.664279 sin(122°)=0.848048,cos(122°)=-0.529919,tan(122°)=-1.600335 sin(123°)=0.838671,cos(123°)=-0.544639,tan(123°)=-1.539865 sin(124°)=0.829038,cos(124°)=-0.559193,tan(124°)=-1.482561 sin(125°)=0.819152,cos(125°)=-0.573576,tan(125°)=-1.428148 sin(126°)=0.809017,cos(126°)=-0.587785,tan(126°)=-1.376382 sin(127°)=0.798636,cos(127°)=-0.601815,tan(127°)=-1.327045 sin(128°)=0.788011,cos(128°)=-0.615661,tan(128°)=-1.279942 sin(129°)=0.777146,cos(129°)=-0.629320,tan(129°)=-1.234897 sin(130°)=0.766044,cos(130°)=-0.642788,tan(130°)=-1.191754 sin(131°)=0.754710,cos(131°)=-0.656059,tan(131°)=-1.150368 sin(132°)=0.743145,cos(132°)=-0.669131,tan(132°)=-1.110613 sin(133°)=0.731354,cos(133°)=-0.681998,tan(133°)=-1.072369 sin(134°)=0.719340,cos(134°)=-0.694658,tan(134°)=-1.035530 sin(135°)=0.707107,cos(135°)=-0.707107,tan(135°)=-1.000000 sin(136°)=0.694658,cos(136°)=-0.719340,tan(136°)=-0.965689 sin(137°)=0.681998,cos(137°)=-0.731354,tan(137°)=-0.932515 sin(138°)=0.669131,cos(138°)=-0.743145,tan(138°)=-0.900404 sin(139°)=0.656059,cos(139°)=-0.754710,tan(139°)=-0.869287 sin(140°)=0.642788,cos(140°)=-0.766044,tan(140°)=-0.839100 sin(141°)=0.629320,cos(141°)=-0.777146,tan(141°)=-0.809784 sin(142°)=0.615661,cos(142°)=-0.788011,tan(142°)=-0.781286 sin(143°)=0.601815,cos(143°)=-0.798636,tan(143°)=-0.753554 sin(144°)=0.587785,cos(144°)=-0.809017,tan(144°)=-0.726543 sin(145°)=0.573576,cos(145°)=-0.819152,tan(145°)=-0.700208 sin(146°)=0.559193,cos(146°)=-0.829038,tan(146°)=-0.674509sin(147°)=0.544639,cos(147°)=-0.838671,tan(147°)=-0.649408 sin(148°)=0.529919,cos(148°)=-0.848048,tan(148°)=-0.624869 sin(149°)=0.515038,cos(149°)=-0.857167,tan(149°)=-0.600861 sin(150°)=0.500000,cos(150°)=-0.866025,tan(150°)=-0.577350 sin(151°)=0.484810,cos(151°)=-0.874620,tan(151°)=-0.554309 sin(152°)=0.469472,cos(152°)=-0.882948,tan(152°)=-0.531709 sin(153°)=0.453990,cos(153°)=-0.891007,tan(153°)=-0.509525 sin(154°)=0.438371,cos(154°)=-0.898794,tan(154°)=-0.487733 sin(155°)=0.422618,cos(155°)=-0.906308,tan(155°)=-0.466308 sin(156°)=0.406737,cos(156°)=-0.913545,tan(156°)=-0.445229 sin(157°)=0.390731,cos(157°)=-0.920505,tan(157°)=-0.424475 sin(158°)=0.374607,cos(158°)=-0.927184,tan(158°)=-0.404026 sin(159°)=0.358368,cos(159°)=-0.933580,tan(159°)=-0.383864 sin(160°)=0.342020,cos(160°)=-0.939693,tan(160°)=-0.363970 sin(161°)=0.325568,cos(161°)=-0.945519,tan(161°)=-0.344328 sin(162°)=0.309017,cos(162°)=-0.951057,tan(162°)=-0.324920 sin(163°)=0.292372,cos(163°)=-0.956305,tan(163°)=-0.305731 sin(164°)=0.275637,cos(164°)=-0.961262,tan(164°)=-0.286745 sin(165°)=0.258819,cos(165°)=-0.965926,tan(165°)=-0.267949 sin(166°)=0.241922,cos(166°)=-0.970296,tan(166°)=-0.249328 sin(167°)=0.224951,cos(167°)=-0.974370,tan(167°)=-0.230868 sin(168°)=0.207912,cos(168°)=-0.978148,tan(168°)=-0.212557 sin(169°)=0.190809,cos(169°)=-0.981627,tan(169°)=-0.194380 sin(170°)=0.173648,cos(170°)=-0.984808,tan(170°)=-0.176327 sin(171°)=0.156434,cos(171°)=-0.987688,tan(171°)=-0.158384 sin(172°)=0.139173,cos(172°)=-0.990268,tan(172°)=-0.140541 sin(173°)=0.121869,cos(173°)=-0.992546,tan(173°)=-0.122785 sin(174°)=0.104528,cos(174°)=-0.994522,tan(174°)=-0.105104 sin(175°)=0.087156,cos(175°)=-0.996195,tan(175°)=-0.087489 sin(176°)=0.069756,cos(176°)=-0.997564,tan(176°)=-0.069927sin(177°)=0.052336,cos(177°)=-0.998630,tan(177°)=-0.052408 sin(178°)=0.034899,cos(178°)=-0.999391,tan(178°)=-0.034921 sin(179°)=0.017452,cos(179°)=-0.999848,tan(179°)=-0.017455 sin(180°)=0.000000,cos(180°)=-1.000000,tan(180°)=-0.000000 sin(181°)=-0.017452,cos(181°)=-0.999848,tan(181°)=0.017455 sin(182°)=-0.034899,cos(182°)=-0.999391,tan(182°)=0.034921 sin(183°)=-0.052336,cos(183°)=-0.998630,tan(183°)=0.052408 sin(184°)=-0.069756,cos(184°)=-0.997564,tan(184°)=0.069927 sin(185°)=-0.087156,cos(185°)=-0.996195,tan(185°)=0.087489 sin(186°)=-0.104528,cos(186°)=-0.994522,tan(186°)=0.105104 sin(187°)=-0.121869,cos(187°)=-0.992546,tan(187°)=0.122785 sin(188°)=-0.139173,cos(188°)=-0.990268,tan(188°)=0.140541 sin(189°)=-0.156434,cos(189°)=-0.987688,tan(189°)=0.158384 sin(190°)=-0.173648,cos(190°)=-0.984808,tan(190°)=0.176327 sin(191°)=-0.190809,cos(191°)=-0.981627,tan(191°)=0.194380 sin(192°)=-0.207912,cos(192°)=-0.978148,tan(192°)=0.212557 sin(193°)=-0.224951,cos(193°)=-0.974370,tan(193°)=0.230868 sin(194°)=-0.241922,cos(194°)=-0.970296,tan(194°)=0.249328 sin(195°)=-0.258819,cos(195°)=-0.965926,tan(195°)=0.267949 sin(196°)=-0.275637,cos(196°)=-0.961262,tan(196°)=0.286745 sin(197°)=-0.292372,cos(197°)=-0.956305,tan(197°)=0.305731 sin(198°)=-0.309017,cos(198°)=-0.951057,tan(198°)=0.324920 sin(199°)=-0.325568,cos(199°)=-0.945519,tan(199°)=0.344328 sin(200°)=-0.342020,cos(200°)=-0.939693,tan(200°)=0.363970 sin(201°)=-0.358368,cos(201°)=-0.933580,tan(201°)=0.383864 sin(202°)=-0.374607,cos(202°)=-0.927184,tan(202°)=0.404026 sin(203°)=-0.390731,cos(203°)=-0.920505,tan(203°)=0.424475 sin(204°)=-0.406737,cos(204°)=-0.913545,tan(204°)=0.445229 sin(205°)=-0.422618,cos(205°)=-0.906308,tan(205°)=0.466308 sin(206°)=-0.438371,cos(206°)=-0.898794,tan(206°)=0.487733sin(207°)=-0.453990,cos(207°)=-0.891007,tan(207°)=0.509525 sin(208°)=-0.469472,cos(208°)=-0.882948,tan(208°)=0.531709 sin(209°)=-0.484810,cos(209°)=-0.874620,tan(209°)=0.554309 sin(210°)=-0.500000,cos(210°)=-0.866025,tan(210°)=0.577350 sin(211°)=-0.515038,cos(211°)=-0.857167,tan(211°)=0.600861 sin(212°)=-0.529919,cos(212°)=-0.848048,tan(212°)=0.624869 sin(213°)=-0.544639,cos(213°)=-0.838671,tan(213°)=0.649408 sin(214°)=-0.559193,cos(214°)=-0.829038,tan(214°)=0.674509 sin(215°)=-0.573576,cos(215°)=-0.819152,tan(215°)=0.700208 sin(216°)=-0.587785,cos(216°)=-0.809017,tan(216°)=0.726543 sin(217°)=-0.601815,cos(217°)=-0.798636,tan(217°)=0.753554 sin(218°)=-0.615661,cos(218°)=-0.788011,tan(218°)=0.781286 sin(219°)=-0.629320,cos(219°)=-0.777146,tan(219°)=0.809784 sin(220°)=-0.642788,cos(220°)=-0.766044,tan(220°)=0.839100 sin(221°)=-0.656059,cos(221°)=-0.754710,tan(221°)=0.869287 sin(222°)=-0.669131,cos(222°)=-0.743145,tan(222°)=0.900404 sin(223°)=-0.681998,cos(223°)=-0.731354,tan(223°)=0.932515 sin(224°)=-0.694658,cos(224°)=-0.719340,tan(224°)=0.965689 sin(225°)=-0.707107,cos(225°)=-0.707107,tan(225°)=1.000000 sin(226°)=-0.719340,cos(226°)=-0.694658,tan(226°)=1.035530 sin(227°)=-0.731354,cos(227°)=-0.681998,tan(227°)=1.072369 sin(228°)=-0.743145,cos(228°)=-0.669131,tan(228°)=1.110613 sin(229°)=-0.754710,cos(229°)=-0.656059,tan(229°)=1.150368 sin(230°)=-0.766044,cos(230°)=-0.642788,tan(230°)=1.191754 sin(231°)=-0.777146,cos(231°)=-0.629320,tan(231°)=1.234897 sin(232°)=-0.788011,cos(232°)=-0.615661,tan(232°)=1.279942 sin(233°)=-0.798636,cos(233°)=-0.601815,tan(233°)=1.327045 sin(234°)=-0.809017,cos(234°)=-0.587785,tan(234°)=1.376382 sin(235°)=-0.819152,cos(235°)=-0.573576,tan(235°)=1.428148 sin(236°)=-0.829038,cos(236°)=-0.559193,tan(236°)=1.482561sin(237°)=-0.838671,cos(237°)=-0.544639,tan(237°)=1.539865 sin(238°)=-0.848048,cos(238°)=-0.529919,tan(238°)=1.600335 sin(239°)=-0.857167,cos(239°)=-0.515038,tan(239°)=1.664279 sin(240°)=-0.866025,cos(240°)=-0.500000,tan(240°)=1.732051 sin(241°)=-0.874620,cos(241°)=-0.484810,tan(241°)=1.804048 sin(242°)=-0.882948,cos(242°)=-0.469472,tan(242°)=1.880726 sin(243°)=-0.891007,cos(243°)=-0.453990,tan(243°)=1.962611 sin(244°)=-0.898794,cos(244°)=-0.438371,tan(244°)=2.050304 sin(245°)=-0.906308,cos(245°)=-0.422618,tan(245°)=2.144507 sin(246°)=-0.913545,cos(246°)=-0.406737,tan(246°)=2.246037 sin(247°)=-0.920505,cos(247°)=-0.390731,tan(247°)=2.355852 sin(248°)=-0.927184,cos(248°)=-0.374607,tan(248°)=2.475087 sin(249°)=-0.933580,cos(249°)=-0.358368,tan(249°)=2.605089 sin(250°)=-0.939693,cos(250°)=-0.342020,tan(250°)=2.747477 sin(251°)=-0.945519,cos(251°)=-0.325568,tan(251°)=2.904211 sin(252°)=-0.951057,cos(252°)=-0.309017,tan(252°)=3.077684 sin(253°)=-0.956305,cos(253°)=-0.292372,tan(253°)=3.270853 sin(254°)=-0.961262,cos(254°)=-0.275637,tan(254°)=3.487414 sin(255°)=-0.965926,cos(255°)=-0.258819,tan(255°)=3.732051 sin(256°)=-0.970296,cos(256°)=-0.241922,tan(256°)=4.010781 sin(257°)=-0.974370,cos(257°)=-0.224951,tan(257°)=4.331476 sin(258°)=-0.978148,cos(258°)=-0.207912,tan(258°)=4.704630 sin(259°)=-0.981627,cos(259°)=-0.190809,tan(259°)=5.144554 sin(260°)=-0.984808,cos(260°)=-0.173648,tan(260°)=5.671282 sin(261°)=-0.987688,cos(261°)=-0.156434,tan(261°)=6.313752 sin(262°)=-0.990268,cos(262°)=-0.139173,tan(262°)=7.115370 sin(263°)=-0.992546,cos(263°)=-0.121869,tan(263°)=8.144346 sin(264°)=-0.994522,cos(264°)=-0.104528,tan(264°)=9.514364 sin(265°)=-0.996195,cos(265°)=-0.087156,tan(265°)=11.430052 sin(266°)=-0.997564,cos(266°)=-0.069756,tan(266°)=14.300666sin(267°)=-0.998630,cos(267°)=-0.052336,tan(267°)=19.081137 sin(268°)=-0.999391,cos(268°)=-0.034899,tan(268°)=28.636253 sin(269°)=-0.999848,cos(269°)=-0.017452,tan(269°)=57.289962 sin(270°)=-1.000000,cos(270°)=-0.000000,tan(270°)=无意义sin(271°)=-0.999848,cos(271°)=0.017452,tan(271°)=-57.289962 sin(272°)=-0.999391,cos(272°)=0.034899,tan(272°)=-28.636253 sin(273°)=-0.998630,cos(273°)=0.052336,tan(273°)=-19.081137 sin(274°)=-0.997564,cos(274°)=0.069756,tan(274°)=-14.300666 sin(275°)=-0.996195,cos(275°)=0.087156,tan(275°)=-11.430052 sin(276°)=-0.994522,cos(276°)=0.104528,tan(276°)=-9.514364 sin(277°)=-0.992546,cos(277°)=0.121869,tan(277°)=-8.144346 sin(278°)=-0.990268,cos(278°)=0.139173,tan(278°)=-7.115370 sin(279°)=-0.987688,cos(279°)=0.156434,tan(279°)=-6.313752 sin(280°)=-0.984808,cos(280°)=0.173648,tan(280°)=-5.671282 sin(281°)=-0.981627,cos(281°)=0.190809,tan(281°)=-5.144554 sin(282°)=-0.978148,cos(282°)=0.207912,tan(282°)=-4.704630 sin(283°)=-0.974370,cos(283°)=0.224951,tan(283°)=-4.331476 sin(284°)=-0.970296,cos(284°)=0.241922,tan(284°)=-4.010781 sin(285°)=-0.965926,cos(285°)=0.258819,tan(285°)=-3.732051 sin(286°)=-0.961262,cos(286°)=0.275637,tan(286°)=-3.487414 sin(287°)=-0.956305,cos(287°)=0.292372,tan(287°)=-3.270853 sin(288°)=-0.951057,cos(288°)=0.309017,tan(288°)=-3.077684 sin(289°)=-0.945519,cos(289°)=0.325568,tan(289°)=-2.904211 sin(290°)=-0.939693,cos(290°)=0.342020,tan(290°)=-2.747477 sin(291°)=-0.933580,cos(291°)=0.358368,tan(291°)=-2.605089 sin(292°)=-0.927184,cos(292°)=0.374607,tan(292°)=-2.475087 sin(293°)=-0.920505,cos(293°)=0.390731,tan(293°)=-2.355852 sin(294°)=-0.913545,cos(294°)=0.406737,tan(294°)=-2.246037 sin(295°)=-0.906308,cos(295°)=0.422618,tan(295°)=-2.144507 sin(296°)=-0.898794,cos(296°)=0.438371,tan(296°)=-2.050304sin(297°)=-0.891007,cos(297°)=0.453990,tan(297°)=-1.962611 sin(298°)=-0.882948,cos(298°)=0.469472,tan(298°)=-1.880726 sin(299°)=-0.874620,cos(299°)=0.484810,tan(299°)=-1.804048 sin(300°)=-0.866025,cos(300°)=0.500000,tan(300°)=-1.732051 sin(301°)=-0.857167,cos(301°)=0.515038,tan(301°)=-1.664279 sin(302°)=-0.848048,cos(302°)=0.529919,tan(302°)=-1.600335 sin(303°)=-0.838671,cos(303°)=0.544639,tan(303°)=-1.539865 sin(304°)=-0.829038,cos(304°)=0.559193,tan(304°)=-1.482561 sin(305°)=-0.819152,cos(305°)=0.573576,tan(305°)=-1.428148 sin(306°)=-0.809017,cos(306°)=0.587785,tan(306°)=-1.376382 sin(307°)=-0.798636,cos(307°)=0.601815,tan(307°)=-1.327045 sin(308°)=-0.788011,cos(308°)=0.615661,tan(308°)=-1.279942 sin(309°)=-0.777146,cos(309°)=0.629320,tan(309°)=-1.234897 sin(310°)=-0.766044,cos(310°)=0.642788,tan(310°)=-1.191754 sin(311°)=-0.754710,cos(311°)=0.656059,tan(311°)=-1.150368 sin(312°)=-0.743145,cos(312°)=0.669131,tan(312°)=-1.110613 sin(313°)=-0.731354,cos(313°)=0.681998,tan(313°)=-1.072369 sin(314°)=-0.719340,cos(314°)=0.694658,tan(314°)=-1.035530 sin(315°)=-0.707107,cos(315°)=0.707107,tan(315°)=-1.000000 sin(316°)=-0.694658,cos(316°)=0.719340,tan(316°)=-0.965689 sin(317°)=-0.681998,cos(317°)=0.731354,tan(317°)=-0.932515 sin(318°)=-0.669131,cos(318°)=0.743145,tan(318°)=-0.900404 sin(319°)=-0.656059,cos(319°)=0.754710,tan(319°)=-0.869287 sin(320°)=-0.642788,cos(320°)=0.766044,tan(320°)=-0.839100 sin(321°)=-0.629320,cos(321°)=0.777146,tan(321°)=-0.809784 sin(322°)=-0.615661,cos(322°)=0.788011,tan(322°)=-0.781286 sin(323°)=-0.601815,cos(323°)=0.798636,tan(323°)=-0.753554 sin(324°)=-0.587785,cos(324°)=0.809017,tan(324°)=-0.726543 sin(325°)=-0.573576,cos(325°)=0.819152,tan(325°)=-0.700208 sin(326°)=-0.559193,cos(326°)=0.829038,tan(326°)=-0.674509sin(327°)=-0.544639,cos(327°)=0.838671,tan(327°)=-0.649408 sin(328°)=-0.529919,cos(328°)=0.848048,tan(328°)=-0.624869 sin(329°)=-0.515038,cos(329°)=0.857167,tan(329°)=-0.600861 sin(330°)=-0.500000,cos(330°)=0.866025,tan(330°)=-0.577350 sin(331°)=-0.484810,cos(331°)=0.874620,tan(331°)=-0.554309 sin(332°)=-0.469472,cos(332°)=0.882948,tan(332°)=-0.531709 sin(333°)=-0.453990,cos(333°)=0.891007,tan(333°)=-0.509525 sin(334°)=-0.438371,cos(334°)=0.898794,tan(334°)=-0.487733 sin(335°)=-0.422618,cos(335°)=0.906308,tan(335°)=-0.466308 sin(336°)=-0.406737,cos(336°)=0.913545,tan(336°)=-0.445229 sin(337°)=-0.390731,cos(337°)=0.920505,tan(337°)=-0.424475 sin(338°)=-0.374607,cos(338°)=0.927184,tan(338°)=-0.404026 sin(339°)=-0.358368,cos(339°)=0.933580,tan(339°)=-0.383864 sin(340°)=-0.342020,cos(340°)=0.939693,tan(340°)=-0.363970 sin(341°)=-0.325568,cos(341°)=0.945519,tan(341°)=-0.344328 sin(342°)=-0.309017,cos(342°)=0.951057,tan(342°)=-0.324920 sin(343°)=-0.292372,cos(343°)=0.956305,tan(343°)=-0.305731 sin(344°)=-0.275637,cos(344°)=0.961262,tan(344°)=-0.286745 sin(345°)=-0.258819,cos(345°)=0.965926,tan(345°)=-0.267949 sin(346°)=-0.241922,cos(346°)=0.970296,tan(346°)=-0.249328 sin(347°)=-0.224951,cos(347°)=0.974370,tan(347°)=-0.230868 sin(348°)=-0.207912,cos(348°)=0.978148,tan(348°)=-0.212557 sin(349°)=-0.190809,cos(349°)=0.981627,tan(349°)=-0.194380 sin(350°)=-0.173648,cos(350°)=0.984808,tan(350°)=-0.176327 sin(351°)=-0.156434,cos(351°)=0.987688,tan(351°)=-0.158384 sin(352°)=-0.139173,cos(352°)=0.990268,tan(352°)=-0.140541 sin(353°)=-0.121869,cos(353°)=0.992546,tan(353°)=-0.122785 sin(354°)=-0.104528,cos(354°)=0.994522,tan(354°)=-0.105104 sin(355°)=-0.087156,cos(355°)=0.996195,tan(355°)=-0.087489 sin(356°)=-0.069756,cos(356°)=0.997564,tan(356°)=-0.069927sin(357°)=-0.052336,cos(357°)=0.998630,tan(357°)=-0.052408 sin(358°)=-0.034899,cos(358°)=0.999391,tan(358°)=-0.034921 sin(359°)=-0.017452,cos(359°)=0.999848,tan(359°)=-0.017455 sin(360°)=-0.000000,cos(360°)=1.000000,tan(360°)=-0.000000。

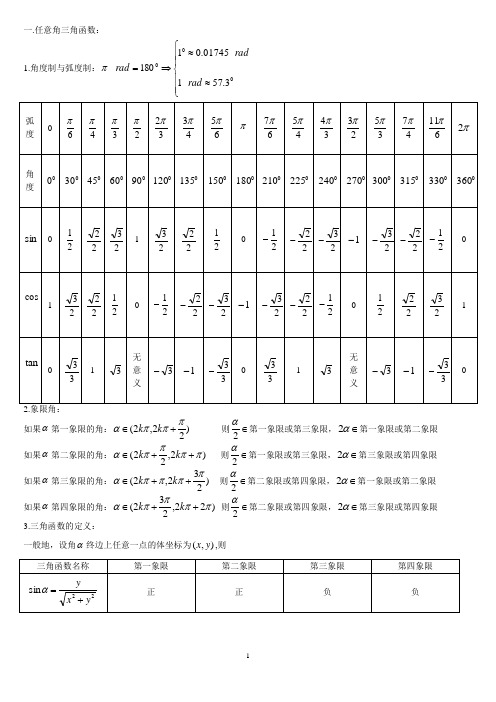
一.任意角三角函数：1.角度制与弧度制：0180=rad π⎪⎪⎩⎪⎪⎨⎧≈≈⇒003.57101745.01rad rad2.象限角：如果α第一象限的角：)22,2(πππα+∈k k 则∈2α第一象限或第三象限，∈α2第一象限或第二象限 如果α第二象限的角：)2,22(ππππα++∈k k 则∈2α第一象限或第三象限，∈α2第三象限或第四象限如果α第三象限的角：)232,2(ππππα++∈k k 则∈2α第二象限或第四象限，∈α2第一象限或第二象限如果α第四象限的角：)22,232(ππππα++∈k k 则∈2α第二象限或第四象限，∈α2第三象限或第四象限3.三角函数的定义：一般地，设角α终边上任意一点的体坐标为),(y x ,则二.三角公式1.同角三函数的关系:1cos sin 22=+αα αααcos sin tan =αα22cos 11tan =+ 2.诱导公式：主要应用于α的三个三角函数值与)(2Z k k ∈⋅+πα的三个三角函数值之间的关系（“奇变偶不变，符号看象限” 、“全、S 、T 、C”）(注：这里面所说的“奇”和“偶”指的是2π的系数k ,如果k 是奇数，则三角函数中的正弦变成余弦，余弦变成正弦，如果是偶数，则不改变三角函数的名称。

正负号由)(2Z k k ∈⋅+πα的象限决定)(1)⎪⎩⎪⎨⎧=+∈=+=+,tan )2tan()(,cos )2cos(,sin )2sin(απααπααπαk z k k k 其中 )(函数值相等终边相同的角的各三角 (2)⎪⎩⎪⎨⎧=++-=+-=+,tan )tan()(,cos )cos(,sin )sin(ααπαπααπααπ是第三象限角其中 (3)⎪⎩⎪⎨⎧-=-=--=-,tan )tan(),,(,cos )cos(,sin )sin(αααααα而余弦是偶函数正切是奇函数其中正弦 (4)⎪⎩⎪⎨⎧-=---=-=-,tan )tan()(,cos )cos(,sin )sin(ααπαπααπααπ是第二象限角其中 (5))2(,sin )2cos(,cos )2sin(是第一象限角其中απααπααπ-⎪⎪⎩⎪⎪⎨⎧=-=- (6)⎪⎪⎩⎪⎪⎨⎧-=--=-,sin )23cos(,cos )23sin(ααπααπ)23(是第三象限角其中απ-(7)⎪⎪⎩⎪⎪⎨⎧-=+=+,sin )2cos(,cos )2sin(ααπααπ)2(是第二象限角其中απ+ (8)⎪⎪⎩⎪⎪⎨⎧=+-=+,sin )23cos(,cos )23sin(ααπααπ)23(是第四象限角其中απ+ (9) ⎪⎪⎩⎪⎪⎨⎧=--=--,sin )23cos(,cos )23sin(ααπααπ)23(是第一象限角其中απ-- (10) ⎪⎪⎩⎪⎪⎨⎧-=---=--,sin )2cos(,cos )2sin(ααπααπ)23(是第三象限角其中απ-- (11) ⎪⎩⎪⎨⎧-=-----=--=--,tan )tan()(,cos )cos(,sin )sin(ααπαπααπααπ是第二象限角其中 3.两角和与差的三角函数公式:βαβαβαsin cos cos sin )sin(±=± βαβαβαsin sin cos cos )cos( =±βαβαβαtan tan 1tan tan )tan( ±=±4.二倍角公式⎪⎪⎩⎪⎪⎨⎧-=-=-=-=-=--=-+==ααααααααααααααααα244222222tan 1tan 22tan sin cos 1cos 2sin 21sin cos 2cos )cos (sin 11)cos (sin cos sin 22sin5.半角公式⎪⎪⎪⎩⎪⎪⎪⎨⎧+-=-=+=αααααααcos 1cos 12tan 2cos 12sin 2cos 12cos 222(降幂扩角公式)αααααααcos 1cos 1sin cos 1cos 1sin 2tan+-±=-=+=6.积化和差公式⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--+-=-++=--+=-++=)]cos()[cos(21sin sin )]cos()[cos(21cos cos )]sin()[sin(21sin cos )]sin()[sin(21cos sin βαβαβαβαβαβαβαβαβαβαβαβα 7.和差化积公式⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-+-=--+=+-+=--+=+2sin2sin 2cos cos 2cos 2cos 2cos cos 2sin 2cos 2sin sin 2cos 2sin 2sin sin βαβαβαβαβαβαβαβαβαβαβαβα 8.辅助角的三角函数公式],[)sin(cos sin 222222b a b a b a b a y ++-∈±+=±=ϕααα)tan ,cos ,sin (2222a bb a ab a b =+=+=ϕϕϕ其中9.关于一般三角函数)sin(ϕω+=x A y 的性质(0,0>>ωA )(1)振幅：A (2)||2:min ωπ=+T 周期 (3)T f 1:=频率πω2||= (4)ϕω+x :相位 (5)ϕ:初相 10.正弦函数：x y sin =(1)定义域：R x ∈ (2)值域：]1,1[-∈y (3)单调性：↓++∈↑+-∈]232,22[,]22,22[ππππππππk k x k k x(4)周期性:最小正周期为π2 (5)奇偶性:奇函数 (6)对称轴方程:2ππ+=k x ,相邻两条对称轴间的距离是最小正周期的一半.(7)当自变量取对称轴时,函数值取得最大值或最小值. (8)当22ππ+=k x 时,函数取最大值1;(9)当232ππ+=k x 时,函数取最小值－1.(10)相邻的两个最大值之间的水平距离是一个最小正周期; (11)相邻的两个最小值之间的水平距离是一个最小正周期;(12)相邻的一个最大值和一个最小值之间的水平距离是一个最小正周期的一半. (13)对称点: )0,(πk ,相邻的两个对称点间的距离是最小正周期的一半. 11.余弦函数x y cos =(1)定义域:∈x R (2)值域]1.1[:-∈y (3)单调性：↑++∈↓+∈]22,2[,]2,2[πππππππk k x k k x (4)周期性:最小正周期为π2(5)奇偶性:偶函数(6)对称轴方程:πk x =(7)相邻两条对称轴间的距离是最小正周期的一半 (8)当自变量取对称轴时,函数值取得最大值或最小值 (9)当πk x 2=时,函数取最大值1(10)当ππ+=k x 2时,函数取最小值－1(11)相邻的两个最大值之间的水平距离是一个最小正周期 (12)相邻的两个最小值之间的水平距离是一个最小正周期(13)相邻的一个最大值和一个最小值之间的水平距离是一个最小正周期的一半.(14)对称点方程: )0,2(ππ+k12.正切函数x y tan =(1)定义域: 2ππ+≠k x(2)值域R y ∈: (3)单调性：↑+-∈)2,2(ππππk k x(4)周期性:最小正周期为π (5)奇偶性:奇函数 (6)对称点方程: )0,(πk13.图象变换：由x y sin =到)sin(ϕω+=x A y +B 的图像变换：(1)值域:]||,||[B A B A y ++-∈(2)单调区间(利用复合函数的“同增异减”原理来判定)当0>ω时:○1]22,22[ππππϕω+-∈+k k x 解出x 的区是为单调递增区间○2]232,22[ππππϕω++∈+k k x 解出x 的区是为单调递减区间 当0<ω时:○1]232,22[ππππϕω++∈+k k x 解出x 的区是为单调递增区间 ○2]22,22[ππππϕω+-∈+k k x 解出x 的区是为单调递减区间(3)对称轴方程的求法:令2ππϕω+=+k x 解出x 并注明Z k ∈(4)对称点的求法: 令πϕωk x =+解出x 并注明Z k ∈(5)限定定义域求值域：根据定义域x 的范围求出ϕω+x 的范围，然后根据三角函数的图象求出)sin(ϕω+x 的范围，进而求出)sin(ϕω+=x A y 的范围.。

所有的三角函数及名称说到三角函数，哎哟，那可真是让很多同学头疼的一个话题。

你一听到“正弦、余弦、正切”这些名词，脑袋瓜就开始冒烟，心里默默想：“这啥玩意儿，咋弄啊？”三角函数啊，说白了，就是跟三角形有关系的数学小工具，帮助我们解决一些看起来复杂的几何问题。

你知道吗，三角函数并不是天外飞来的仙丹，它就像是你生活中的万能钥匙，能解开很多你看似无法解决的问题。

大家别着急，先深呼吸，跟我一起慢慢捋一下这些“怪兽”到底是什么。

首先得从三角形说起。

你想，三角形是由三条边和三个角组成的，听起来挺简单对吧？不过，实际上一些角度和边长之间的关系，直接决定了你能否找到那个完美的解。

三角函数就是用来描述这些关系的，像个秘密小帮手。

大家听说过“三角函数”这个词，它包括了正弦（sin）、余弦（cos）、正切（tan）这几个大名鼎鼎的角色。

你想，正弦和余弦就是这帮小伙伴中最“稳”的两个，正切就像个“搞笑担当”，总是让你捧腹大笑，但有时候也会把你弄得晕头转向。

先说正弦和余弦吧，简直是数学中的黄金搭档。

它们俩的关系特别简单，正弦就是三角形的对边长度和斜边长度的比，余弦呢，就是邻边长度和斜边长度的比。

说白了，正弦是站在三角形的对面，余弦则站在邻近你角度的旁边。

你试着想象一下，正弦和余弦像两个闺蜜，一个总是站在你面前，另一个则躲在你身旁。

它们俩总是形影不离，相互补充，让你在面对角度的时候，能更好地看清楚对比的关系。

然后啊，说到正切，那可是个活宝。

正切就是正弦和余弦的“合体”，它是正弦和余弦的比值。

就是那种，你吃了一块蛋糕，它吃了另一块，两者结合，你俩就可以一起组成一个新甜品了。

正切也是三角函数中的“野路子”，它不仅能够让你解题，还能给你带来一些意外的惊喜。

你看，正切特别像那种社交达人，总是能一蹦一跳地把你带入各种情况，但有时候它也让你差点头晕目眩，尤其是当角度达到90度时，正切就会失控，变成个大无穷，哎呀，这时候你得小心了，不然就容易“翻车”。

单位圆定义六个三角函数也可以依据半径为1中心为原点的单位圆来定义。

单位圆定义在实际计算上没有大的价值；实际上对多数角它都依赖于直角三角形。

但是单位圆定义的确允许三角函数对所有正数和负数辐角都有定义，而不只是对于在 0 和π/2 弧度之间的角。

它也提供了一个图像，把所有重要的三角函数都包含了。

根据勾股定理，三角函数单位圆的方程是：x^2+y^2=1图像中给出了用弧度度量的一些常见的角。

逆时针方向的度量是正角，而顺时针的度量是负角。

设一个过原点的线，同x轴正半部分得到一个角θ，并与单位圆相交。

这个交点的x和y坐标分别等于 cos θ和 sin θ。

图像中的三角形确保了这个公式；半径等于斜边且长度为1，所以有 sin θ = y/1 和 cos θ = x/1。

单位圆可以被视为是通过改变邻边和对边的长度，但保持斜边等于 1的一种查看无限个三角形的方式。

对于大于 2π或小于等于2π的角度，可直接继续绕单位圆旋转。

在这种方式下，正弦和余弦变成了周期为 2π的周期函数：对于任何角度θ和任何整数k。

周期函数的最小正周期叫做这个函数的“基本周期”。

正弦、余弦、正割或余割的基本周期是全圆，也就是 2π弧度或360°；正切或余切的基本周期是半圆，也就是π弧度或180°。

上面只有正弦和余弦是直接使用单位圆定义的，其他四个三角函数的定义如图所示。

其他四个三角函数的定义在正切函数的图像中，在角kπ附近变化缓慢，而在接近角 (k+ 1/2)π的时候变化迅速。

正切函数的图像在θ = (k + 1/2)π有垂直渐近线。

这是因为在θ从左侧接进 (k + 1/2)π的时候函数接近正无穷，而从右侧接近 (k + 1/2)π的时候函数接近负无穷。

另一方面，所有基本三角函数都可依据中心为O的单位圆来定义，类似于历史上使用的几何定义。

特别三角函数是，对于这个圆的弦AB，这里的θ是对向角的一半，sin θ是AC（半弦），这是印度的阿耶波多介入的定义。

完整三角函数公式表三角函数公式表同角三角函数的基本关系式三角函数之间有着特定的关系，这些关系被称为同角三角函数的基本关系式。

其中，倒数关系包括tanα ·cotα＝1、sinα ·cscα＝1和cosα ·secα＝1；商的关系包括sinα/cosα＝tanα＝secα/cscα和cosα/sinα＝cotα＝cscα/secα；平方关系包括sinα＋cosα＝1、221＋tanα＝secα和221＋cotα＝cscα。

这些关系可以用六边形记忆法来记忆，也可以用其他方法来记忆。

诱导公式诱导公式是指通过某些变换，将一个三角函数转化为另一个三角函数的公式。

其中，口诀“奇变偶不变，符号看象限”可以帮助我们记忆。

例如，sin（－α）＝－sinα、cos（－α）＝cosα、tan（－α）＝－tanα和cot（－α）＝－cotα。

此外，还有其他的诱导公式，如sin（3π/2－α）＝－cosα、cos（3π/2－α）＝－sinα、sin（2π－α）＝－sinα、cos（2π－α）＝cosα等。

两角和与差的三角函数公式两角和与差的三角函数公式可以将两个角的三角函数转化为一个角的三角函数。

其中，sin（α＋β）＝sinαcosβ＋cosαsinβ、sin（α－β）＝sinαcosβ－cosαsinβ和cos（α＋β）＝cosαcosβ－sinαsinβ是两角和的公式，而sin（α＋β）＝sinαcosβ－cosαsinβ、cos（α－β）＝cosαcosβ＋sinαsinβ和cos （α＋β）＝cosαcosβ＋sinαsinβ是两角差的公式。

这些公式可以帮助我们简化计算。

cos（α－β）可以用cosαcosβ＋sinαsinβ表示。

tan（α＋β）可以用tanα＋tanβ和1－tanα·tanβ的倒数表示。

万能公式是2tan(α/2) = sinα/(1+cosα)和cosα/(1+sinα)。

sin tan cos三角函数表前言在数学领域中，三角函数是一类非常重要的函数，其中最常见的三个是正弦函数（sin）、余弦函数（cos）和正切函数（tan）。

它们在数学运算、物理学和工程学中都有广泛的应用。

本文将介绍sin、tan、cos三角函数的基本定义、性质和常用数值范围，以及它们在实际问题中的应用。

正弦函数sin正弦函数是最基础的三角函数之一，通常表示为sin(x)，其中x为自变量（弧度）。

正弦函数的定义域为实数集，值域为[-1, 1]。

正弦函数在二维平面上表示了单位圆上的点的y 坐标。

若角度为x度，则sin(x)表示单位圆上与对应角度相对应的点的y坐标值。

余弦函数cos余弦函数是另一个常见的三角函数，通常表示为cos(x)，其中x为自变量（弧度）。

余弦函数的定义域也为实数集，值域为[-1, 1]。

余弦函数在二维平面上表示了单位圆上的点的x坐标。

若角度为x度，则cos(x)表示单位圆上与对应角度相对应的点的x坐标值。

正切函数tan正切函数是第三个常见的三角函数，通常表示为tan(x)，其中x为自变量（弧度）。

正切函数的定义域为实数集，但在特定点上会有无定义的情况（如π/2 + nπ）。

正切函数的值域为实数集，即它可以取任意实数值。

三角函数表下面是一些常见角度下sin、tan、cos函数的数值表：角度（度）正弦值sin余弦值cos正切值tan0010300.5√3/2√3/345√2/2√2/2160√3/20.5√39010无定义应用举例三角函数在数学、物理、工程等领域有广泛的应用。

例如，在物理学的力学中，三角函数可以用来描述物体受到的力和受力方向之间的关系；在工程学中，三角函数可以用来分析电路中的交流信号波形等。

因此，熟练掌握三角函数的性质和应用是非常重要的。

总结本文介绍了三角函数sin、tan、cos的定义、性质和常用数值范围，以及它们在实际问题中的应用。

通过学习和掌握三角函数的基本知识，读者可以更好地理解数学和物理问题，提高解决问题的能力。

sin tan cos三角函数表三角函数是数学中的重要概念，它们在几何学、物理学、工程学等学科中发挥着重要的作用。

其中，sin、tan和cos是最常用的三角函数之一。

本文将给出它们的数值表格，方便读者查找和使用。

1. sin函数表角度（度）弧度值sin值00030π/60.545π/40.70760π/30.86690π/21180π0 2703π/2-1 3602π02. tan函数表角度（度）弧度值tan值00030π/60.577 45π/4160π/3 1.732 90π/2无穷大180π0 2703π/2无穷大3602π03. cos函数表角度（度）弧度值cos值00130π/60.866 45π/40.707 60π/30.590π/20180π-12703π/203602π1以上表格列出了常见角度下sin、tan和cos的值。

其中，“度”表示角度，可以理解为我们通常所用的角度单位；“弧度值”则是以弧度为单位表示的角度值；“sin值”、“tan值”和“cos 值”分别表示对应角度下的sin、tan和cos函数值。

需要注意的是，由于sin和cos函数的值在一个周期内是周期性的，所以在表格中我们仅列出了一个周期内的部分角度值。

读者可以根据需要进行推算，得到其他角度下的函数值。

另外，要特别注意角度为90度和270度时，tan函数的值为无穷大。

这是因为在这两个角度时，cos函数的值为0，而根据tan函数的定义，tan值等于sin值除以cos值，此时导致分母为0，从而导致tan值无穷大。

以上就是sin、tan和cos三角函数的数值表格，希望这个表格能够帮助到读者在数学计算和应用中使用三角函数。

在实际应用中，需要根据具体问题的需求使用适当的函数值，以达到相应的计算和分析效果。