用枚举法设计算法

谈谈用枚举算法解决问题的编程思路与步骤方法一．问题上海市普通高中在信息科技学科中开展《算法与程序设计》教学，教材中有一章名为“算法实例”的内容，其中有一节介绍“枚举算法”。

教材中关于枚举算法的描述：有一类问题可以采用一种盲目的搜索方法，在搜索结果的过程中，把各种可能的情况都考虑到，并对所得的结果逐一进行判断，过滤掉那些不合要求的，保留那些符合要求的。

这种方法叫做枚举算法（enumerative algorithm）。

枚举法就是按问题本身的性质，一一列举出该问题所有可能的解，并在逐一列举的过程中，检验每个可能解是否是问题的真正解，若是，我们采纳这个解，否则抛弃它。

在列举的过程中，既不能遗漏也不应重复。

生活和工作中，人们经常会不经意间运用“枚举算法”的基本原理，进行问题的解决。

比如，让你用一串钥匙，去开一把锁，但是不知道具体是用哪一把钥匙，你就会一把一把地挨个地逐个尝试，最终打开锁为止。

又如，要对1000个零件，进行合格检验，等等。

二．用枚举算法的思想编写程序的思路与步骤枚举算法，归纳为八个字：一一列举，逐个检验。

在实际使用中，一一列举；采用循环来实现，逐个检验：采用选择来实现。

下面，通过一个问题的解决来说明这一类问题的解决过程的方法与步骤；例1：在1—2013这些自然数中，找出所有是37倍数的自然数。

这个问题就可以采用枚举算法来解决：1)．一一列举；采用循环来实现；循环需要确定范围：本循环控制变量假设用i，起始值是1，终止值是2013。

2)．逐个检验：采用选择来实现；选择需要列出判断的关系表达式：i Mod 37 = 0这样，就可以写出整个求解的VB代码：Dim i As IntegerFor i = 1 To 2013If i Mod 37 = 0 ThenPrint iEnd IfNext i说白了，用枚举算法解决问题，其实是利用计算机的高速度这一个优势，就好比上题完全可以使用一张纸和一支笔，采用人工的方法完成问题的解，从1开始，一一试除以37，这样计算2013次，也可以找到问题的答案。

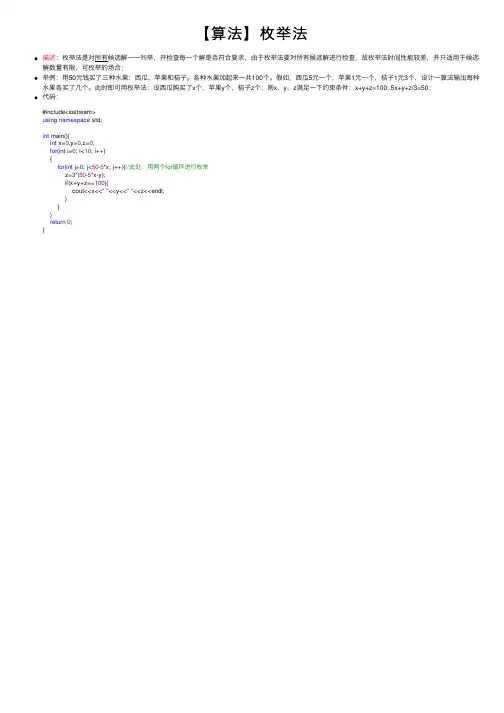
【算法】枚举法
描述：枚举法是对所有候选解⼀⼀列举，并检查每⼀个解是否符合要求，由于枚举法要对所有候选解进⾏检查，故枚举法时间性能较差，并只适⽤于候选解数量有限、可枚举的场合；
举例：⽤50元钱买了三种⽔果：西⽠、苹果和桔⼦。

各种⽔果加起来⼀共100个。

假如，西⽠5元⼀个，苹果1元⼀个，桔⼦1元3个，设计⼀算法输出每种⽔果各买了⼏个。

此时即可⽤枚举法：设西⽠购买了x个，苹果y个，桔⼦z个；则x、y、z满⾜⼀下约束条件：x+y+z=100; 5x+y+z/3=50；
代码：
#include<iostream>
using namespace std;
int main(){
int x=0,y=0,z=0;
for(int i=0; i<10; i++)
{
for(int j=0; j<50-5*x; j++){//此处，⽤两个for循环进⾏枚举
z=3*(50-5*x-y);
if(x+y+z==100){
cout<<x<<""<<y<<""<<z<<endl;
}
}
}
return0;
}。

枚举算法的步骤介绍枚举算法是一种简单却有效的解决问题的方法。

它通过穷举所有可能的解决方案来找到问题的解。

本文将详细介绍枚举算法的步骤，包括问题描述、解设计、穷举和解决方案验证。

通过深入了解枚举算法的步骤，读者可以更好地理解和应用这一算法。

问题描述首先，我们需要明确问题的描述。

问题描述应该清晰而具体，直观地表达问题的要求和限制。

在枚举算法中，问题描述是我们开始设计解决方案的基础。

解设计解设计是指为了解决问题而设计的解决方案的结构和思路。

在枚举算法中，解设计是整个算法的核心。

下面是解设计的一些重要步骤：确定问题解空间问题解空间是指问题的所有可能的解决方案构成的空间。

在枚举算法中，我们需要明确问题解空间的结构和范围，以便穷举所有可能的解。

制定解决方案的表示解决方案的表示是指如何表示问题的解。

这个表示应该能够表示问题的所有可能解，并能够在算法中被穷举和验证。

设计解穷举的算法解穷举是指枚举算法中穷举解空间的过程。

设计解穷举的算法需要考虑解的范围和解的顺序，以便能够穷举所有可能的解，并将其作为解决方案的候选。

解决方案的验证解决方案的验证是指对穷举出来的解进行筛选和验证，以确认其是否满足问题的要求和限制。

解决方案的验证是保证最终解是正确的关键。

穷举穷举是指枚举算法中对解空间进行遍历的过程。

在穷举过程中，我们逐个尝试解空间中的解，并对其进行验证。

为了实现穷举，我们需要使用循环和条件判断等控制结构。

一般来说，我们会使用嵌套循环来穷举所有可能的组合。

解决方案验证解决方案验证是指对穷举出来的解进行筛选和验证的过程。

通过解决方案验证，我们可以确定哪些解是满足问题要求和限制的。

解决方案验证可以包括以下步骤：检查解的有效性首先，我们需要检查解是否满足问题的约束条件。

这些约束条件可以是数学方程、逻辑条件等。

如果解不满足约束条件，那么该解是无效的，我们应该继续穷举其他解。

检查解的优劣除了满足约束条件外，我们还需要评估解的优劣。

谈谈用枚举算法解决问题的编程思路与步骤方法一．问题上海市普通高中在信息科技学科中开展《算法与程序设计》教学，教材中有一章名为“算法实例”的内容，其中有一节介绍“枚举算法”。

教材中关于枚举算法的描述：有一类问题可以采用一种盲目的搜索方法，在搜索结果的过程中，把各种可能的情况都考虑到，并对所得的结果逐一进行判断，过滤掉那些不合要求的，保留那些符合要求的。

这种方法叫做枚举算法（enumerative algorithm）。

枚举法就是按问题本身的性质，一一列举出该问题所有可能的解，并在逐一列举的过程中，检验每个可能解是否是问题的真正解，若是，我们采纳这个解，否则抛弃它。

在列举的过程中，既不能遗漏也不应重复。

生活和工作中，人们经常会不经意间运用“枚举算法”的基本原理，进行问题的解决。

比如，让你用一串钥匙，去开一把锁，但是不知道具体是用哪一把钥匙，你就会一把一把地挨个地逐个尝试，最终打开锁为止。

又如，要对1000个零件，进行合格检验，等等。

二．用枚举算法的思想编写程序的思路与步骤枚举算法，归纳为八个字：一一列举，逐个检验。

在实际使用中，一一列举；采用循环来实现，逐个检验：采用选择来实现。

下面，通过一个问题的解决来说明这一类问题的解决过程的方法与步骤；例1：在1—2013这些自然数中，找出所有是37倍数的自然数。

这个问题就可以采用枚举算法来解决：1)．一一列举；采用循环来实现；循环需要确定范围：本循环控制变量假设用i，起始值是1，终止值是2013。

2)．逐个检验：采用选择来实现；选择需要列出判断的关系表达式：i Mod 37 = 0这样，就可以写出整个求解的VB代码：Dim i As IntegerFor i = 1 To 2013If i Mod 37 = 0 ThenPrint iEnd IfNext i说白了，用枚举算法解决问题，其实是利用计算机的高速度这一个优势，就好比上题完全可以使用一张纸和一支笔，采用人工的方法完成问题的解，从1开始，一一试除以37，这样计算2013次，也可以找到问题的答案。

枚举法是一种通过列举所有可能情况来解决问题的方法。

对于1到100的数字，我们可以使用Python的for循环来枚举所有的数字。

以下是一个简单的Python程序，使用枚举法找出1到100之间的所有奇数：python复制代码for i in range(1, 101):if i % 2 != 0:print(i)这个程序会打印出1到100之间的所有奇数。

range(1, 101)函数生成一个从1到100的数字序列，然后for 循环遍历这个序列。

在循环中，我们使用if语句检查当前的数字是否是奇数（即除以2的余数不等于0），如果是，就打印出来。

如果你想找出1到100之间的所有素数，你可以使用一个稍微复杂的算法，比如埃拉托斯特尼筛法（Sieve of Eratosthenes）。

这个算法的基本思想是，从2开始，把所有的偶数都标记为合数，然后找出所有的未被标记的数字，这些数字就是素数。

以下是一个使用Python实现的埃拉托斯特尼筛法的例子：python复制代码def sieve_of_eratosthenes(n):primes = [True] * (n+1)primes[0] = primes[1] = Falsefor i in range(2, int(n**0.5)+1):if primes[i]:for j in range(i**2, n+1, i):primes[j] = Falsereturn [p for p in range(2, n+1) if primes[p]]print(sieve_of_eratosthenes(100))这个程序会打印出1到100之间的所有素数。

8算法策略之枚举法蛮⼒法蛮⼒法是基于计算机运算速度快这⼀特性，在解决问题时采取的⼀种“懒惰”的策略。

这种策略不经过（或者说是经过很少的）思考，把问题的所有情况或所有过程交给计算机去⼀⼀尝试，从中找出问题的解。

蛮⼒策略的应⽤很⼴，具体表现形式各异，数据结构课程中学习的：选择排序、冒泡排序、插⼊排序、顺序查找、朴素的字符串匹配等，都是蛮⼒策略具体应⽤。

⽐较常⽤还有枚举法、盲⽬搜索算法等。

枚举法枚举（ enumerate）法（穷举法）是蛮⼒策略的⼀种表现形式，也是⼀种使⽤⾮常普遍的思维⽅法。

它是根据问题中的条件将可能的情况⼀⼀列举出来，逐⼀尝试从中找出满⾜问题条件的解。

但有时⼀⼀列举出的情况数⽬很⼤，如果超过了我们所能忍受的范围，则需要进⼀步考虑，排除⼀些明显不合理的情况，尽可能减少问题可能解的列举数⽬。

⽤枚举法解决问题，通常可以从两个⽅⾯进⾏算法设计：1）找出枚举范围：分析问题所涉及的各种情况。

2）找出约束条件：分析问题的解需要满⾜的条件，并⽤逻辑表达式表⽰。

【例1】百钱百鸡问题。

中国古代数学家张丘建在他的《算经》中提出了著名的“百钱百鸡问题”：鸡翁⼀，值钱五；鸡母⼀，值钱三；鸡雏三，值钱⼀；百钱买百鸡，翁、母、雏各⼏何?算法设计1：通过对问题的理解，读者可能会想到列出两个三元⼀次⽅程，去解这个不定解⽅程，就能找出问题的解。

这确实是⼀种办法，但这⾥我们要⽤“懒惰”的枚举策略进⾏算法设计：设x，y，z分别为公鸡、母鸡、⼩鸡的数量。

尝试范围：由题意给定共100钱要买百鸡，若全买公鸡最多买100/5=20只，显然x的取值范围1~20之间；同理，y的取值范围在1~33之间，z的取值范围在1~100之间。

约束条件： x+y+z=100 且 5*x+3*y+z/3=100算法1如下：main( ){ int x,y,z;for(x=1;x<=20;x=x+1)for(y=1;y<=34;y=y+1)for(z=1;z<=100;z=z+1)if(100=x+y+z and 100=5*x+3*y+z/3){print("the cock number is",x)；print("the hen number is", y)；print("the chick number is“,z);}}算法分析：以上算法需要枚举尝试20*34*100=68000次。

python枚举算法例子简单枚举算法是一种常用的算法思想，它通过列举所有可能的情况来解决问题。

枚举算法在解决一些简单问题时非常有效，但对于复杂的问题可能会导致计算量过大，因此需要谨慎使用。

以下是一些常见的使用枚举算法解决问题的例子：1.查找数组中的最大值和最小值：给定一个整数数组，我们可以使用枚举算法来查找其中的最大值和最小值。

我们可以使用两个变量分别记录当前找到的最大值和最小值，然后遍历数组，依次比较每个元素与当前最大值和最小值的大小关系，更新最大值和最小值。

2.找到数组中的两个元素使其和为给定值：给定一个整数数组和一个目标值，我们可以使用枚举算法来找到数组中的两个元素，使其和等于目标值。

我们可以使用两层循环遍历数组中的所有元素，对于每对元素，判断它们的和是否等于目标值。

如果找到了满足条件的元素，就输出它们的索引或值。

3.找到数组中的三个元素使其和为给定值：类似地，我们也可以使用枚举算法来找到数组中的三个元素，使其和等于给定值。

这可以通过使用三层循环遍历数组中的所有元素来实现。

对于每三个元素的组合，判断它们的和是否等于目标值。

如果找到了满足条件的三个元素，就输出它们的索引或值。

4.穷举法解决密码破解问题：某种密码由4个数字组成，每个数字的范围是0-9之间的一个整数。

穷举法可以用来解决这类密码破解问题。

我们可以使用四层循环来穷举所有可能的密码组合，并与已知密码进行比对，直到找到正确的密码。

这种方法在密码位数较少、可能取值较少的情况下比较实用。

5.枚举所有子串：给定一个字符串，枚举所有可能的子串是一个常见的问题。

我们可以使用两层循环来遍历字符串的所有可能的起始和结束索引，并输出对应的子串。

这种方法可以帮助我们快速检查字符串中是否包含指定的子串。

以上例子只是枚举算法的一些基本应用，实际上枚举算法可以应用在很多不同的问题中。

但需要注意的是，由于枚举算法需要遍历所有可能的情况，所以在解决复杂问题时会导致计算量过大，效率较低。

枚举算法之算法实现枚举算法是一种常用的算法设计思想，其核心思想是通过遍历所有可能的解空间，逐一枚举所有可能的解，并通过比较得到最优解。

枚举算法的实现一般包括以下几个步骤：1.确定问题的解空间：首先需要明确问题的解空间是什么，即问题的可能解有哪些。

对于一些简单的问题，解空间可能是固定的范围，如整数的解空间是[0,n]；对于一些复杂的问题，解空间可能需要通过一些规律和约束来确定。

2.枚举所有可能的解：确定了解空间后，就可以通过循环或递归来枚举解空间中的所有可能解。

如果解空间是一个固定的范围，可以使用循环来遍历解空间中的每一个值；如果解空间是不定的，可以使用递归来遍历解空间中的每一个可能。

3.判断解的有效性：对于问题的解，可能不是所有的解都是有效的解，需要通过一些条件来判断解的有效性。

如果解无效，可以直接跳过或排除该解，减少后续的计算量。

4.比较得到最优解：在枚举的过程中，需要将当前枚举得到的解与当前最优解进行比较，并根据问题的要求更新最优解。

最优解可以是最大值、最小值、最优组合等，根据具体问题而定。

枚举算法的实现需要一定的时间复杂度，因为需要遍历解空间中的所有解。

对于解空间较大的问题，枚举算法的时间复杂度可能会非常高，甚至是指数级的。

在实际应用中，需要根据具体问题的规模和要求来选择是否使用枚举算法。

下面以两个例子来说明枚举算法的实现。

1. 求解在一个整数数组中找到两个数之和等于给定值的问题。

假设给定一个整数数组arr和目标值target，需要找到两个数a和b，使得a + b = target。

可以使用枚举算法来遍历数组中的每一个数，并用目标值减去当前数字，看是否存在解。

具体实现如下：```pythondef findTwoSum(arr, target):for i in range(len(arr)):for j in range(i + 1, len(arr)):if arr[i] + arr[j] == target:return [i, j]return []arr = [2, 7, 11, 15]target = 9print(findTwoSum(arr, target)) # 输出[0, 1]```2.求解在一个字符串中找到最长的回文子串的问题。