抛物线平移、对称变换

函数图象变换和零点一、函数图像1、平移变换Ⅰ、水平平移：函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向左(0)a >或向右(0)a <平移||a 个单位即可得到；1）y =f (x )h 左移→y =f (x +h)； 2）y =f (x ) h右移→y =f (x -h)；Ⅱ、竖直平移：函数()y f x a =+的图像可以把函数()y f x =的图像沿x 轴方向向上(0)a >或向下(0)a <平移||a 个单位即可得到；1）y =f (x ) h 上移→y =f (x )+h ； 2）y =f (x ) h下移→y =f (x )-h 。

2、对称变换Ⅰ、函数()y f x =-的图像可以将函数()y f x =的图像关于y 轴对称即可得到；y =f (x ) 轴y →y =f (-x ) Ⅱ、函数()y f x =-的图像可以将函数()y f x =的图像关于x 轴对称即可得到；y =f (x ) 轴x →y = -f (x ) Ⅲ、函数()y f x =--的图像可以将函数()y f x =的图像关于原点对称即可得到；y =f (x ) 原点→y = -f (-x ) Ⅳ、函数)(y f x =的图像可以将函数()y f x =的图像关于直线y x =对称得到。

y =f (x ) xy =→直线x =f (y )Ⅴ、函数)2(x a f y -=的图像可以将函数()y f x =的图像关于直线a x =对称即可得到；y =f (x )ax =→直线y =f (2a -x )。

3、翻折变换Ⅰ、函数|()|y f x =的图像可以将函数()y f x =的图像的x 轴下方部分沿x 轴翻折到x 轴上方，去掉原x 轴下方部分，并保留()y f x =的x 轴上方部分即可得到；Ⅱ、函数(||)y f x =的图像可以将函数()y f x =的图像右边沿y 轴翻折到y 轴左边替代原y 轴左边部分并保留()y f x =在y 轴右边部分即可得到4、伸缩变换Ⅰ、函数()y af x =(0)a >的图像可以将函数()y f x =的图像中的每一点横坐标不变纵坐标伸长(1)a >或压缩（01a <<）为原来的a 倍得到；y =f (x )ay ⨯→y =af (x )Ⅱ、函数()y f ax =(0)a >的图像可以将函数()y f x =的图像中的每一点纵坐标不变横坐标伸长(1)a >或压缩（01a <<）为原来的1a倍得到。

二次函数图像变换
二次函数图像变换有3种：平移、对称、旋转。

一、专用解法
1、平移：左加右减自变量，上加下减常数项
2、对称、旋转：取原抛物线上一点（x,y），然后根据对称或旋转规律找到对应点，
将对应点坐标代入原抛物线解析式，然后化解得到的解析式即所求。

例1：原抛物线上y=ax^2+bx+c有一点（x,y），其关于x轴对称的点坐标为（x,-y），将（x,-y）代入到原解析式得到-y=ax^2+bx+c，即y=-ax^2-bx-c
例2：原抛物线上y=x^2+2x绕点（1,0）旋转180°，求旋转后的解析式解：设点（x,y）是原抛物线y=x^2+2x上一点，（x,y）绕点（1,0）旋转180°，通过中点坐标公式得出对应点为（2-x,-y），将（2-x,-y）代入y=x^2+2x得到
-y=(2-x)^2+2(2-x)，即y=-x^2+6x-8
注意：以上方法也适用于一次函数
二、通用解法
①将解析式化顶点式y=a(x-h)^2+k，得到顶点（h,k）
②将顶点（h,k）按照要求进行平移、对称、旋转，得到新的顶点（h’,k’）
③平移a不变；X轴对称a变号，Y轴对称a不变；旋转a变号，特别的原点对称就是绕（0,0）旋转180
注意：这里的旋转肯定是180°，因为如果不是180°得到的就不是二次函数了
④知道了a和顶点，设顶点式就可以得到新抛物线的解析式
注意：无论平移、对称、旋转都可以用，如果是一次函数可以将顶点（h,k）替换为直线与y轴交点，a替换为k，整体思路是一样的。

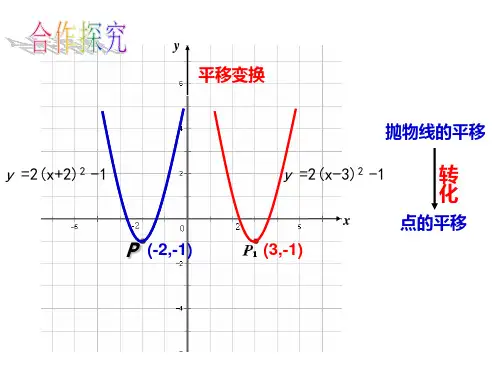
抛物线平移、对称变换的规律一、平移变换 如果二次函数解析式为一般式2y ax bx c =++，应先化成顶点式2()y a x h k =-+，然后按照“左加右减，上加下减”的规律去推导. 例1、（2010 兰州）抛物线2y x bx c =++的图像向右平移2个单位长度，再向下平移3个单位长度，所得图像的解析式为：223y x x =--，则b ，c 的值为（ ） A . 2b =,2c = B . 2b =, 0c = C . 2b =-，1c =- D .3b =-，2c =【解析】：采用逆推法，把223y x x =--向左平移2个单位，再向上平移3个单 位可得到2y x bx c =++，把223y x x =--配方得：222113(1)4y x x x =-+--=--，根据平移规律得2222(12)43(1)12112y x x x x x x =-+-+=+-=++-=+，故选B二、对称变换⑴关于x 轴对称：坐标系内一点(,)P x y 关于x 轴的对称点的坐标为(,)x y -，所以把(,)x y -代入原抛物线2y ax bx c =++后得新解析式为2y ax bx c -=++，整理得 2y ax bx c =---. ⑵关于y 轴对称：坐标系内一点(,)P x y 关于y 轴的对称点坐标为(,)x y -，把(,)x y -代入原抛物线2y ax bx c =++后得新解析式为22()()y a x b x c ax bx c =-+-+=-+. ⑶关于原点对称：坐标系内一点(,)P x y 关于原点的对称点坐标为(,)x y --，把(,)x y --代入原抛物线2y ax bx c =++后得新解析式为2()()y a x b x c -=-+-+，整理得2y ax bx c =-+-.实战演练：①（2009 黔东南）二次函数23y x x =--的图像关于原点(0,0)O 对称的图像的解析式为----------------- （答案：223y x x =--+） ②（2009 重庆）在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴对称变换，再将所得的抛物线关于y 轴做对称变换，那么两次变换后所得到的新抛物线解析式为（ ）A . 22y x x =--+B . 22y x x =-+-C . 22y x x =-++D . 22y x x =++答案：C .。

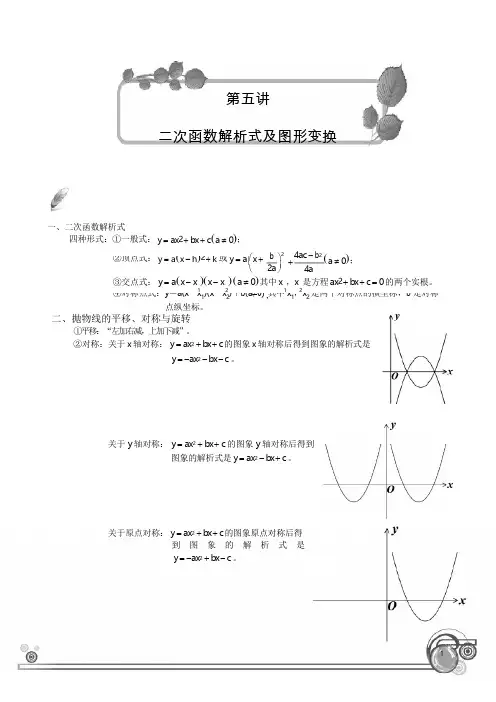
②顶点式： y = a (x - h )2 + k 或 y = a x +⎪ + ④对称点式：y ＝a(x －x 1)(x －x 2)＋b (a ≠0) 其中 x 1，x 2 是两个对称点的横坐标，b 是对称第五讲二次函数解析式及图形变换一、二次函数解析式四种形式：①一般式： y = ax 2 + bx + c (a ≠ 0)；⎛ ⎝b ⎫2 2a ⎭4ac - b 2 (a ≠ 0)； 4a③交点式： y = a (x - x )(x - x ) (a ≠ 0) 其中 x ，x 是方程 ax 2 + b x + c = 0 的两个实根。

1 2 1 2， 点纵坐标。

二、抛物线的平移、对称与旋转①平移：“左加右减，上加下减”。

②对称：关于 x 轴对称： y = ax 2 + b x + c 的图象 x 轴对称后得到图象的解析式是y = -ax 2 - b x - c 。

关于 y 轴对称： y = ax 2 + b x + c 的图象 y 轴对称后得到图象的解析式是 y = ax 2 - b x + c 。

关于原点对称： y = ax 2 + b x + c 的图象原点对称后得到 图 象 的 解 析 式 是 y = -ax 2 + b x - c 。

1．求二次函数 y = ax 2 + b x + c 与直线 y = kx + m 的交点，联立方程组 ⎨ 求解。

2．求二次函数 y = a x 2+ b x + c 与 y = a x 2+ b x + c 的交点，联立方程组 ⎨ 求解。

⎧⎪ y = a x 2 + b x + c ⎪⎩ y = a x 2 + b x + c ⑶（2007 朝阳二模）已知抛物线 y = ax 2 + b x(a ≠ 0) 的顶点在直线 y = -x - 1 上，当且仅当 ⑵请探索：是否存在二次项系数的绝对值小于 的整点抛物线？若存在，请写出其中一条抛物线三、二次函数与一元二次方程⎧ y = ax 2 + bx + c ⎩ y = kx + m1 1 1 1 1 12 2 2 2 2 2板块一 二次函数解析式【例1】 ⑴ 下列说法不正确的是（）A ．抛物线 y = ax 2 + b x - 3 与 y 轴的交点为 (0 ，- 3)B ．抛物线 y = ax 2 - 2ax + a 2 - 1 的对称轴为 x = 1C ．抛物线 y = ax 2 - a (m + 1)x + ma 与 x 轴的交点为 (m ，0)和 (1，0)D ．抛物线 y = a (x + π )2 - x 的顶点坐标为 (-π ，- x )⑵（2009 三帆单元测试）已知抛物线 y = ax 2 + bx + c 经过点 A (-1，0)，且经过直线 y = x - 3 与x 轴的交点 B 及与 y 轴的交点 C ，则抛物线的解析式为。

2012（主要内容）抛物线的平移、轴对称、旋转变换1、抛物线()223y x =+-可以由抛物线2y x =平移得到,则下列叙述正确的是( )A.先向左平移2个单位,再向上平移3个单位B.先向左平移2个单位,再向下平移3个单位C.先向右平移2个单位,再向下平移3个单位D.先向右平移2个单位,再向上平移3个单位 2、抛物线223x y =向右平移3个单位，再向上平移2个单位，则所得抛物线的解析式 。

3、抛物线5)2(212+--=x y 可以由抛物线1)1(212+--=x y 先向 平移 个单位，再向 平移 个单位得到的。

4、（ 2011庆江津）将抛物线y=x 2－2x 向上平移3个单位,再向右平移4个单位得到的抛物线是____ ___5、函数2x y =的图像与函数2x y -=的图像关于 对称。

6、已知抛物线742+-=x x y(1)写出与它关于y 轴对称的抛物线的解析式 。

(2)写出与它关于x 轴对称的抛物线的解析式 。

(3)写出与它关于原点中心对称的抛物线的解析式 。

(4)写出它绕着顶点旋转180°后得到的抛物线的解析式 。

(5)向右平移 个单位，图像经过点(5,4)。

(6)向下平移 个单位，图像也经过点(5,4)。

7、(2009年鄂州)把抛物线y ＝ax 2+bx+c 的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是y ＝x 2－3x+5，则求a+b+c 的.8、（2009宁波市）如图，抛物线254y ax ax a =-+与x 轴相交于点A 、B ，且过点(54)C ，． （1）求a 的值和该抛物线顶点P 的坐标；（2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．9、（2009年衢州）如图，已知点A (-4，8)和点B (2，n )在抛物线2y ax =上．(1) 求a 的值及点B 关于x 轴对称点P 的坐标，并在x 轴上找一点Q ，使得AQ +QB 最短，求出点Q 的坐标；(2) 平移抛物线2y ax =，记平移后点A 的对应点为A ′，点B 的对应点为B ′，点C (-2，0)和点D (-4，0)是x 轴上的两个定点．① 当抛物线向左平移到某个位置时，A ′C +CB ′ 最短，求此时抛物线的函数解析式； ② 当抛物线向左或向右平移时，是否存在某个位置，使四边形A ′B ′CD 的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．A BPxyOC （5,4）4 x2 2A8 -2 O-2 -4 y 6 B C D -44。

二次函数专题训练（平移、旋转、轴对称变换）一、二次函数图象的平移、旋转（只研究中心对称）、轴对称变换 1、抛物线的平移变换：一般都是在顶点式的情况下进行的。

y=a(x-h)²+k y=a(x-h)²+k ±my=a(x-h)² y=a(x-h ±m)²+k 练习：（1）函数图象沿y 轴向下平移2个单位，再沿x 轴向右平移3个单位，得到函数__________________的图象。

（2）抛物线225y x x =-+向左平移3个单位，再向下平移6个单位，所得抛物线的解析式是 。

2、抛物线的旋转变换（只研究中心对称）：一般都是在顶点式的情况下进行的。

（1）将抛物线绕其顶点旋转180︒（即两条抛物线关于其顶点成中心对称） ()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+。

（2）将抛物线绕原点旋转180︒（即两条抛物线关于原点成中心对称）()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-。

练习：（1）抛物线2246y x x =-+绕其顶点旋转180︒后，所得抛物线的解析式是 （2）将抛物线y ＝x 2＋1绕原点O 旋转180°，则旋转后抛物线的解析式为( ) A ．y ＝－x 2 B ．y ＝－x 2＋1 C ．y ＝x 2－1 D ．y ＝－x 2－1 3、抛物线的轴对称变换： 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---； ()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+； ()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；练习：已知抛物线C 1：2(2)3y x =-+（1）抛物线C 2与抛物线C 1关于y 轴对称，则抛物线C 2的解析式为 （2）抛物线C 3与抛物线C 1关于x 轴对称，则抛物线C 3的解析式为 总结：根据平移、旋转、轴对称的性质，显然无论作何种变换，抛物线的形状一定不会发生变化，因此a 永远不变。

2二次函数图象的平移、旋转、轴对称专题有关图象的变换一般可采用两种基本的方法，其一是利用特殊点进行变换，其二是利用坐标变换的规律进行变换。

所谓利用特殊点进行变换，即选取原图象上一些特殊的点，把这些点按指定的要求进行变换，再把变换后的点代入到新的解析式中，从而求出变换后的解析式，利用特殊点进行变换，又可以从一般形式入手，选取图象上的三个特殊的点进行变换，也可以把一般形式化为顶点式，选取顶点作为特殊点，然后进行变换。

利用坐标变换的方法，根据题目的要求，利用坐标变换的规律，从而进行变换。

下面由具体的例子进行说明。

一 、 平 移 。

例1、 把抛物线 y=x -4x+6 向左平移 3 个单位，再向下平移 4 个单位后，求其图象的解析式。

法（一）选取图象上三个特殊的点，如（0， 6），（ 1， 3），（ 2，2）【选取使运算最简单的点】，然后把这三个点按要求向左平移3 个单位，再向下平移4 个单位后得到三个新点（ -3 ， 2），（ -2 ， -1 ），（-1 ，-2 ），把这三个新点代入到新的函数关 系式的一般形式 y=ax 2+bx+c 中，求出各项系数即可。

例 2、已知抛物线 y=2x 位，求其解析式。

法（二）2-8x+5, 求其向上平移 4 个单位，再向右平移 3 个单先利用配方法把二次函数化成y a( x h)2 k 的形式，确定其顶点（ 2，-3 ），然后把顶点（ 2， -3 ）向上平移 4 个单位，再向右平移 3 个单位后得到新抛物线的顶点为（ 5， 1），因为是抛物线的平移，因此平移前后 a 的值应该相等，这样我们就得到新的抛物线的解析式中 a=2，且顶点为（ 5， 1），就可以求出其解析式了。

22222【平移规律：在原有函数的基础上“左加右减、上加下减”】 .法（三）根据平移规律进行平移，不论哪种抛物线的形式，平移规律为 “左右平移即把解析式中自变量 x 改为 x 加上或减去一个常数，左加右减，上下平移即把整个解析式加上或减去一个常数，上加下减。

专题30 函数图象的平移与变换知识对接考点一、函数图象的变换一 、平移变换函数图象的平移变换，表现在函数图象的形状不变，只是函数图象的相对位置在变化，其平移方式可分为以下两种：①沿水平方向左右平行移动②沿竖直方向上下平行移动1．利用描点法作函数的图象的基本步骤：①确定函数的定义域②简化函数的解析式③讨论函数的性质(奇偶性、单调性、最值等)④画出函数的图象2．图象的平移变换①)0)((>-=a a x f y 的图象可由)(x f y =的图象沿x 轴向右平移a 个单位得到；)0)((>+=a a x f y 的图象可由)(x f y =的图象沿x 轴向左平移a 个单位得到②)0()(>±=h h x f y 的图象可由)(x f y =的图象沿y 轴向上或向下平移h 个单位得到注意：（1）可以将平移变换化简成口诀：左加右减，上加下减（2）谁向谁变换是)(x f y =→)(a x f y -=还是)(a x f y -=→)(x f y =二、对称变换图象的对称性是函数在对称区间上值域具有不同特点的直观反应，函数图象的对称性反应在两个方面，一是两个函数图象间的对称情况，二是一个函数图象本身的对称情况。

两个函数图象间的对称情况有两种形式：一是两图关于某条直线对称，二是两图象关于某点呈中心对称。

①)(x f y =与)(x y -=)的图象关于y 轴对称②)(x f y =与)(x y -=的图象关于x 轴对称③)(x f y =与)(x y -=的图象关于原点对称 ④)(x f y =的图象是保留)(x f y =的图象中位于上半平面内的部分，及与x 轴的交点，将)(x f y =的)图象中位于下半平面内的部分以x 轴为对称翻折到上半面中去而得到。

⑤()x f y =图象是保留中位于右半面内的部分及与y 轴的交点，去掉左半平面内的部分，而利用偶函数的性质，将右半平面内的部分以y 轴为对称轴翻转到左半平面中去而得到。

各种变换下抛物线解析式的求法实施变换之前的抛物线记为ab ac ab x ac bx axy 44)2(222-++=++=经过某种变换其顶点坐标由)44,2(2ab ac a b A --变为),('k h A一、抛物线的平移变换性质1：抛物线向右平移m 个单位长度，再向上平移n 个单位长度后，所得抛物线的解析式为：（1）顶点式为)44()2(22a b ac n a b m x a y -++⎥⎦⎤⎢⎣⎡--=；（2）一般式为nc m x b m x a y ++-+-=)()(2其中的m 与n 均可正可负，还可为0，例如：向左平移3个单位长度，则m=-3；向下平移4个单位长度，则n=-4；左右不平移时m=0；上下不平移时n=0 例1 把抛物线8762+-=x xy 作如下变换，求所得的抛物线的解析式：（1）向左平移2个单位长度；（2）向上平移3个单位长度；（3）先向右平移3个单位长度，再向下平移2个单位长度。

答案：（1）181762++=x xy ；（2）11762+-=x xy ；（3）814362+-=x xy二、抛物线的轴对称变换 1、关于直线x=m 对称性质2：关于直线x=m 对称的抛物线的解析式为： （1）顶点式为a b ac a b m x a y 44)22(22-+⎥⎦⎤⎢⎣⎡+-=；（2）一般式为cm x b m x a y +---=)2()2(2特别地：当m=0时，直线x=0即为y 轴，关于y 轴对称的抛物线为：（1）顶点式为ab ac a b x a y 44)2(22-+-=；（2）一般式为cbx axy +-=2例2 把抛物线4322-+=x x y ，求所得的抛物线的解析式：（1）关于y 轴对称；（2）关于直线x=-2对称；（3）关于直线x=1对称； 答案：（1）4322--=x xy ；（2）161322++=x xy ；（3）101122+-=x xy2、关于直线y=n 对称性质3：关于直线y=n 对称的抛物线的解析式为：（1）顶点式为)442()2(22a b ac n a b x a y --+⎥⎦⎤⎢⎣⎡---=；（2）一般式为n c bx axy 22+---=特别地：当n=0时，直线y=0即为x 轴，关于x 轴对称的抛物线为：（1）顶点式为ab ac a b x a y 44)]2([22-----=；（2）一般式为c bx axy ---=2例3 将抛物线6422+-=x x y 作如下变换，求所得的抛物线的解析式：（1）关于x 轴对称；（2）关于直线y=2；（3）关于直线y=-3对称。

专题提优3 抛物线与几何变换———专题讲解———一、抛物线的平移 （1）具体步骤：先利用配方法将二次函数化成y =a （x －h ）2＋k 的形式，确定其顶点（h ，k ），然后作出二次函数y =ax 2的图象，将抛物线y =ax 2平移，使其顶点平移到（h ，k ）．具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减”． 二、抛物线的对称二次函数图象的对称一般有五种情况： ①关于x 轴对称：y =ax 2＋bx ＋c 关于x 轴对称后，得到的解析式是y =－ax 2－bx －c ；y =a （x －h ）2＋k 关于x 轴对称后，得到的解析式是y =－a （x －h ）2－k ． ②关于y 轴对称：y =ax 2＋bx ＋c 关于y 轴对称后，得到的解析式是y =ax 2－bx ＋c ；y =a （x －h ）2＋k 关于y 轴对称后，得到的解析式是y =a （x ＋h ）2＋k ． ③关于原点对称：y =ax 2＋bx ＋c 关于原点对称后，得到的解析式是y =－ax 2＋bx －c ；y =a （x －h ）2＋k 关于原点对称后，得到的解析式是y =－a （x ＋h ）2－k ． ④关于顶点对称：y =ax 2＋bx ＋c 关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；y =a （x －h ）2＋k 关于顶点对称后，得到的解析式是()2y a x h k =--+． ⑤关于点（m ，n ）对称：()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．———典型例题———【例1】（2014•陕西）已知抛物线C ：cbx x y ++-=2经过A （－3，0）和B （0，3）两点．将这条抛物线的顶点记为M ，它的对称轴于x 轴的交点记为N ． （1）求抛物线C 的表达式； （2）求点M 的坐标；（3将抛物线C 平移到C′，抛物线C′的顶点记为M′，它的对称轴于x 轴的交点记为N′．如果以点M 、N 、M′、N′为顶点的四边形是面积为16的平行四边形，那么应将抛物线C 怎样平移为什么【提示】根据平行四边形的定义，可知有四种情形符合条件，需要分类讨论．【感悟】1、二次项系数的不变性．抛物线平移中，二次函数中二次项系数是不变的；2、以点带线．顶点的平移方向和平移距离就是抛物线平移的方向和距离，反之，亦然；3、顶点式的应用，是解答抛物线平移的常用公式．既做到由顶点坐标求解析式，又做到能由解析式求出顶点坐标．【例2】（2013•河北省）如图，一段抛物线：y =－x （x －3）（0≤x ≤3），记为C 1，它与x 轴交于点O ，A 1；将C 1绕点A 1旋转180°得C 2，交x 轴于点A 2；将C 2绕点A 2旋转180°得C 3，交x 轴于点A 3；…如此进行下去，直至得C 13．若P （37，m ）在第13段抛物线C 13上，则m = ．【提示】根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式，进而求出m 的值．【方法总结】旋转前后的图形大小与形状都没发生变化．———小试身手———1．（☆☆ 2014•浙江宁波）已知点A （a －2b ，2－4ab ）在抛物线y =x 2＋4x ＋10上，则点A 关于抛物线对称轴的对称点坐标为（ ）A ．（－3，7）B ．（－1，7）C ．（－4，10）D ．（0，10）2．（☆☆ 2012•陕西省）在平面直角坐标系中，将抛物线y =x 2－x －6向上（下）或向左（右）平移m 个单位，使平移后的抛物线恰好经过原点，则|m |的最小值为（ ） A ．1 B ．2 C ．3 D ．63．（☆☆☆2014•山东临沂）在平面直角坐标系中，函数22(y x x x =-≥0)的图象为1C ，1C 关于原点对称的图象为2C ，则直线y a =（a 为常数）与1C ，2C 的交点共有（ ）A ．1个B ．1个或2个C ．1个或2个或3个D ．1个或2个或3个或4个 4．（☆☆☆）如图，抛物线m ：y =ax 2＋b （a ＜0，b ＞0）与x 轴于点A 、B （点A 在点B 的左侧），与y 轴交于点C ．将抛物线m 绕点B 旋转180°，得到新的抛物线n ，它的顶点为C 1，与x 轴的另一个交点为A 1．若四边形AC 1A 1C 为矩形，则a ，b 应满足的关系式为（ ）A ．ab =－2B ．ab =－3C ．ab =－4D ．ab =－5（第4题图） （第5题图）5．（☆☆☆☆2014•西湖区一模）如图，将二次函数y =x 2－m （其中m ＞0）的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，形成新的图象记为y 1，另有一次函数y =x ＋b 的图象记为y 2，则以下说法：（1）当m =1，且y 1与y 2恰好有三个交点时，b 有唯一值为1；（2）当b =2，且y 1与y 2恰有两个交点时，m ＞4或0＜m ＜47；（3）当m =b 时，y 1与y 2至少有2个交点，且其中一个为（0，m ）；（4）当m =－b 时，y 1与y 2一定有交点．其中正确说法的序号为 ．6．（☆☆ 2013•河南省）如图，抛物线的顶点为P （－2，2），与y 轴交于点A （0，3）．若平移该抛物线使其顶点P 沿直线移动到点P′（2，－2），点A 的对应点为A′，则抛物线上PA 段扫过的区域（阴影部分）的面积为 ．7．（☆☆2010•关系桂林）将抛物线y =2x 2－12x ＋16绕它的顶点旋转180°，所得抛物线的解析式是 ．8．（☆☆☆☆2014•湖南衡阳模拟）已知二次函数y =2x 2＋bx ＋1（b 为常数），当b 取不同的值时，对应得到一系列二次函数的图象，它们的顶点都在一条抛物线上，则这条抛物线的解析式是 ；若二次函数y =2x 2＋bx ＋1的顶点只在x 轴上方移动，那么b 的取值范围是 ．9．（☆☆☆2014•贵州贵阳）如图，经过点A （0，－6）的抛物线y =12x 2＋bx ＋c 与x 轴相交于B （－2，0），C 两点． （1）求此抛物线的函数关系式和顶点D 的坐标； （2）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m （m ＞0）个单位长度得到新抛物线y 1，若新抛物线y 1的顶点P 在△ABC 内，求m 的取值范围；（3）在（2）的结论下，新抛物线y 1上是否存在点Q ，使得△QAB 是以AB 为底边的等腰三角形请分析所有可能出现的情况，并直接写出相对应的m 的取值范围．10．（☆☆☆2014•江西抚州）如图，抛物线y =ax 2＋2ax （a＜0）位于x轴上方的图象记为F1，它与x轴交于P1、O两点，图象F2与F1关于原点O对称，F2与x轴的另一个交点为P2，将F1与F2同时沿x轴向右平移P1P2的长度即可得到F3与F4；再将F3与F4同时沿x轴向右平移P1P2的长度即可得到F5与F6；…；按这样的方式一直平移下去即可得到一系列图象F1，F2，…，F n．我们把这组图象称为“波浪抛物线”．（1）当a=－1时，①求图象F1的顶点坐标；②点H（2014，－3）（填“在”或“不在”）该“波浪抛物线”上；若图象F n的顶点T n的横坐标为201，则图象F n对应的解析式为，其自变量x的取值范围为．（2）设图象F n、F n＋1的顶点分别为T n、T n＋1（m为正整数），x轴上一点Q的坐标为（12，0）．试探究：当a为何值时，以O、T n、T n＋1、Q四点为顶点的四边形为矩形并直接写出此时m的值．11．（☆☆☆2014•江苏镇江）如图，在平面直角坐标系xOy中，点M为抛物线y=－x2＋2nx－n2＋2n的顶点，过点（0，4）作x轴的平行线，交抛物线于点P、Q（点P在Q的左侧），PQ=4．（1）求抛物线的函数关系式，并写出点P的坐标；（2）小丽发现：将抛物线y=－x2＋2nx－n2＋2n绕着点P旋转180°，所得新抛物线的顶点恰为坐标原点O，你认为正确吗请说明理由；12．（☆☆☆☆2014•湖南怀化）如图1，在平面直角坐标系中，AB=OB=8，∠ABO=90°，∠yOC=45°，射线OC以每秒2个单位长度的速度向右平行移动，当射线OC经过点B时停止运动，设平行移动x秒后，射线OC扫过Rt△ABO的面积为y．（1）求y与x之间的函数关系式；（2）当x=3秒时，射线OC平行移动到O′C′，与OA相交于G，如图2，求经过G，O，B三点的抛物线的解析式；（3）现有一动点P在（2）中的抛物线上，试问点P在运动过程中，是否存在三角形POB的面积S=8的情况若存在，求出点P的坐标，若不存在，请说明理由．13．（☆☆☆☆☆2014•辽宁盘锦）如图，抛物线y=ax2＋bx＋c经过原点，与x轴相交于点E（8，0 ），抛物线的顶点A在第四象限，点A到x轴的距离AB=4，点P（m，0）是线段OE上一动点，连结PA，将线段PA绕点P逆时针旋转90°得到线段PC，过点C作y轴的平行线交x轴于点G，交抛物线于点D，连结BC和AD．（1）求抛物线的解析式；（2）求点C的坐标（用含m的代数式表示）；（3）当以点A、B、C、D为顶点的四边形是平行四边形时，求点P的坐标．———参考答案———例1．【解析】（1）∵抛物线y=－x2＋bx＋c经过A（－3，0）和B（0，3）两点，∴930,3,b cc--+=⎧⎨=⎩解得2,3.bc=-⎧⎨=⎩故此抛物线的解析式为y=－x2－2x＋3；（2）∵由（1）知抛物线的解析式为y=－x2－2x＋3，∴当x=－22(1)-⨯-=－1时，y=4，∴M（－1，4）．（3）由题意，以点M、N、M′、N′为顶点的平行四边形的边MN的对边只能是M′N′，∴MN∥M′N′且MN=M′N′，∴MN•NN′=16，∴NN′=4．i）当M、N、M′、N′为顶点的平行四边形是▱MNN′M′时，将抛物线C向左或向右平移4个单位可得符合条件的抛物线C′；ii）当M、N、M′、N′为顶点的平行四边形是▱MNM′N′时，将抛物线C先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C′．∴上述的四种平移，均可得到符合条件的抛物线C′．例2．【答案】2【解析】∵一段抛物线：y=－x（x－3）（0≤x≤3），∴图象与x轴交点坐标为：（0，0），（3，0），∵将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3；…如此进行下去，直至得C13．∴C13的解析式与x轴的交点坐标为（36，0），（39，0），且图象在x轴上方，∴C13的解析式为y13=－（x－36）（x－39），当x=37时，y=－（37－36）×（37－39）=2．1．【答案】D【解析】∵点A（a－2b，2－4ab）在抛物线y=x2＋4x＋10上，∴（a－2b）2＋4×（a－2b）＋10=2－4ab，a2－4ab＋4b2＋4a－8b＋10=2－4ab，（a＋2）2＋4（b－1）2=0，∴a＋2=0，b－1=0，解得a=－2，b=1，∴a－2b=－2－2×1=－4，2－4ab=2－4×（－2）×1=10，∴点A的坐标为（－4，10）．∵对称轴为直线x=－421⨯=－2，∴点A关于对称轴的对称点的坐标为（0，10）．2．【答案】B【解析】当x=0时，y=－6，故函数图象与y轴交于点C（0，－6），当y=0时，x2－x－6=0，即（x＋2）（x－3）=0，解得x=－2或x=3，即A（－2，0），B（3，0）；由图可知，函数图象至少向右平移2个单位恰好过原点，故|m|的最小值为2．3．【答案】【解析】C 函数y =x 2－2x （x ≥0）的图象为C 1关于原点对称的图象为C 2的解析式是y =－x 2－2x （x ≤0），观察图象：当a >1或a <－1时，直线y =a 与图象C 1、C 2只有1个交点；当a =1或a =－1时，直线y =a 与图象C 1、C 2有2个交点；当－1<a <1时，直线y =a 与图象C 1、C 2有3个交点． 4．【答案】B【解析】令x =0，得y =b ．∴C （0，b ）．令y =0，得ax 2＋b =0，∴x =±ab-，∴A （－ab -，0），B （ab -，0），∴AB =2ab -，BC =22OB OC +=ab b -2．要使平行四边形AC 1A 1C 是矩形，必须满足AB =BC ，∴2ab -=a b b -2．∴4×（a b -）=b 2－ab，∴ab =－3．∴a ，b 应满足关系式ab =－3． 5．【答案】②③【解析】①当m =1，且y 1与y 2恰好有三个交点时，b 有唯一值为1，b =45，故①错误；②当b =2，且y 1与y 2恰有两个交点时，m ＞4或0＜m ＜47，故②正确；③当m =b 时，y 1与y 2至少有2个交点，且其中一个为（0，m ）故③正确；④当m =－b 时，y 1与y 2没有交点，故④错误． 6．【答案】12【解析】连接AP ，A′P′，过点A 作AD ⊥PP′于点D ，由题意可得出：AP ∥A′P′，AP =A′P′，∴四边形APP′A′是平行四边形．∵抛物线的顶点为P （－2，2），与y 轴交于点A （0，3），平移该抛物线使其顶点P 沿直线移动到点P′（2，－2）， ∴PO =2222+=22，∠AOP =45°，又∵AD ⊥OP ，∴△ADO 是等腰直角三角形，∴PP′=22×2=42，AD =DO =223，∴抛物线上PA 段扫过的区域（阴影部分）的面积为42×223=12．7．【答案】y =－2x 2＋12x －20【解析】y =2x 2－12x ＋16=2（x 2－6x ＋8）=2（x －3）2－2，将原抛物线绕顶点旋转180°后，得y =－2（x －3）2－2=－2x 2＋12x －20．8．【答案】y =－2x 2＋1，－22＜b ＜2【解析】∵y =2x 2＋bx ＋1的顶点坐标是（－4b，288b -），设x =－4b，y =288b -，∴b =－4x ，∴y =288b -=28(4)8x -=－2x 2＋1，若二次函数y =2x 2＋bx ＋1的顶点只在x 轴上方移动，∵a =2＞0，∴抛物线与x 轴没有交点，∴△＜0，即△=b 2－8＜0，9．【解析】（1）将A （0，－6），B （－2，0）代入y =12x 2＋bx ＋c ，得6,022,c b c -=⎧⎨=-+⎩解得2,6.b c =-⎧⎨=-⎩∴y =12x 2－2x －6，∴顶点坐标为（2，－8）； （2）将（1）中求得的抛物线向左平移1个单位长度，再向上平移m （m ＞0）个单位长度得到新抛物线y 1=12（x －2＋1）2－8＋m ，∴P （1，－8＋m ）．在抛物线y =12x 2－2x －6中易得C （6，0），∴直线AC 的解析式为y 2=x －6， 当x =1时，y 2=－5，∴－5＜－8＋m ＜0， 解得3＜m ＜8；（3）∵A （0，－6），B （－2，0），∴线段AB 的中点坐标为（－1，－3），直线AB 的解析式为y =－3x －6， ∴过AB 的中点且与AB 垂直的直线的解析式为y =13x －83， ∴直线y =13x －83与x =1的交点坐标为（1，－73）， ∴此时的点P 的坐标为（1，－73），∴此时向上平移了8－73=173个单位， ∴①当3＜m ＜173时，存在两个Q 点，可作出两个等腰三角形； ②当m =173时，存在一个点Q ，可作出一个等腰三角形； ③当173＜m ＜8时，Q 点不存在，不能作出等腰三角形． 10．【解析】（1）当a =－1时，①y =ax 2＋2ax =－x 2－2x =－（x ＋1）2＋1，∴图象F 1的顶点坐标为（－1，1）； ②∵该“波浪抛物线”顶点坐标纵坐标分别为1和－1，∴点H （2014，－3），不在该“波浪抛物线”上． ∵图象F n 的顶点T n 的横坐标为201，201÷4=50…1，故其图象与F 2，F 4，…形状相同， 则图象F n 对应的解析式为y =（x －201）2－1，其自变量x 的取值范围为200≤x ≤202． 故答案为：不在，y =（x －201）2－1，200≤x ≤202．（2）设OQ 中点为O′，则线段T n T n ＋1经过O′，由题意可知OO′=O′Q ，O′T n =O′T n ＋1， ∴当T n T n ＋1=OQ =12时，四边形OT n T n ＋1Q 为矩形，∴O′T n ＋1=6．∵F 1对应的解析式为y =a （x ＋1）2－a ，∴F 1的顶点坐标为（－1，－a ）， ∴由平移的性质可知，点T n ＋1的纵坐标为－a ，∴由勾股定理得（－a）2＋12=62，∴a∵a＜0，∴a=m的值为4．11．【解析】（1）∵抛物线y=－x2＋2nx－n2＋2n过点P，P点的纵坐标为4，∴4=－x2＋2n x－n2＋2n，解得x1=n，x2=n．∵PQ=x1－x2=4，∴=4，解得n=4，∴抛物线的函数关系式为y=－x2＋8x－8，∴4=－x2＋8x－8，解得x=2或x=6，∴P（2，4）．（2）正确；∵P（2，4），PQ=4，∴Q绕着点P旋转180°后的对称点为Q′（－2，4），∴P与Q′正好关于y轴对称，∴所得新抛物线的对称轴是y轴．∵抛物线y=－x2＋8x－8=－（x－4）2＋8，∴抛物线的顶点M（4，8），∴顶点M到直线PQ的距离为4，∴所得新抛物线顶点到直线PQ的距离为4，∴所得新抛物线顶点应为坐标原点．12．【解析】（1）∵AB=OB，∠ABO=90°，∴△ABO是等腰直角三角形，∴∠AOB=45°，∵∠yOC=45°，∴∠AOC=（90°－45°）＋45°=90°，∴AO⊥CO．∵C′O′是CO平移得到，∴AO⊥C′O′，∴△OO′G是等腰直角三角形．∵射线OC的速度是每秒2个单位长度，∴OO′=2x，∴其以OO′为底边的高为x，∴y=12×（2x）•x=x2；（2）当x=3秒时，OO′=2×3=6，∵12×6=3，∴点G的坐标为（3，3）．设抛物线解析式为y=ax2＋bx，则933,6480,a ba b+=⎧⎨+=⎩解得1,58.5ab⎧=-⎪⎪⎨⎪=⎪⎩∴抛物线的解析式为y=－15x2＋85x；（3）设点P到x轴的距离为h，则S△POB=12×8h=8，解得h=2．当点P在x轴上方时，－15x2＋85x=2，整理得x2－8x＋10=0，解得x1=4，x2=4，此时，点P的坐标为（4，2）或（4，2）；当点P在x轴下方时，－15x2＋85x=－2，整理得x2－8x－10=0，解得x1=4－26，x2=4＋26，此时，点P的坐标为（4－26，－2）或（4＋26，－2）．综上所述，点P的坐标为（4－6，2）或（4＋6，2）或（4－26，－2）或（4＋26，－2）时，△POB的面积S=8．13．【解析】（1）由题意可知A（4，－4），∵抛物线y=ax2＋bx＋c经过原点、点E（8，0 ）和A（4，－4），则0,6480,1644,ca b ca b c=⎧⎪++=⎨⎪++=-⎩解得1,42,0.abc⎧=⎪⎪=-⎨⎪=⎪⎩∴抛物线的解析式为y=14x2－2x．（2）∵∠APC=90°，∴∠APB＋∠CPG=90°．∵AB⊥PE，∴∠APB＋∠PAB=90°，∴∠CPG=∠PAB．∵∠ABP=∠PGC=90°，PC=PA，∴△ABP≌△PGC，PB=CG，AB=PG=4．∵P（m，0），OP=m，且点P是线段OE上的动点，∴PB=CG=|4－m|，OG=|m＋4|．①如图1，当点P在点B左边时，点C在x轴上方，m＜4，4－m＞0，PB=CG=4－m，∴C（m＋4，4－m）；②如图2，当点P在点B右边时，点C在x轴下方，m＞4，4－m＜0，∴PB=|4－m|=－（4－m）=m－4，∴CG=m－4，∴C（m＋4，4－m）．综上所述，点C坐标是C（m＋4，4－m）．（3）如图1，当点P在OB上时，∵CD∥y轴，则CD⊥OE．∵点D 在抛物线上，横坐标是m ＋4，将x =m ＋4代入y =41x 2－2x 得y ＝41(m ＋4)2−2(m ＋4) ， 化简得y ＝41m 2−4，∴D （m ＋4，41m 2−4），CD =4－m －（41m 2−4）=−41m 2−m ＋8． ∵四边形ABCD 是平行四边形，∴AB =CD =4， ∴−41m 2−m ＋8=4，解得m 1＝−2＋25，m 2＝−2−25． ∵点P 在线段OE 上，∴m 2＝−2−25不符合题意，舍去，∴P （−2＋25，0）；如图2，当点P 在线段BE 上时，∵C （m ＋4，4－m ）， ∵点D 在抛物线上，横坐标是m ＋4，将x =m ＋4代入y =41x 2－2x 得y ＝41(m ＋4)2−2(m ＋4)， 化简得y ＝41m 2−4，∴D （m ＋4，41m 2−4）， ∴CD =41m 2−4−(4−m )＝41m 2＋m ＋8． ∵四边形ABDC 是平行四边形，∴AB =CD =4， ∴41m 2＋m −8＝4，解得m 1＝−2＋213，m 2＝−2−213， ∵点P 在线段OE 上，∴m 2＝−2−213不符合题意，舍去，∴P （−2＋213，0）．综上所述，当以点A 、B 、C 、D 为顶点的四边形是平行四边形时，点P 的坐标为P （−2＋25，0）或P （−2＋213，0）．[。

第十讲 抛物线的对称平移问题明确目标﹒定位考点在二次函数一章中抛物线的对称性和平移问题是一个重点内容，也是中考常考的知识点。

掌握其对称和平移的规律能为我们解题带来很多方便，也能为我们从中节省很多时间。

热点聚焦﹒考点突破考点1 抛物线关于x 轴、y 轴、原点、顶点对称的抛物线的解析式。

二次函数图象的对称一般有四种情况，可以用一般式或顶点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3. 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4. 关于顶点对称（即：抛物线绕顶点旋转180°）2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+注： 对于以上四种对称要在结合开个方向、对称轴的位置以及与y 轴的交点三个方面结合图像理解记忆。

而对于抛物线关于定点对称问题我们一般都是化成顶点式再变换.【例1】二次函数432--=x x y 关于Y 轴的对称图象的解析式为 ，关于X 轴的对称图象的解析式为 ，关于原点的对称图象的解析式为 ，关于顶点旋转180度的图象的解析式为 。

【例2】将抛物线221216y x x =-+绕它的顶点旋转180°，所得抛物线的解析式是（ ）．A ．221216y x x =--+B ．221216y x x =-+-C ．221219y x x =-+- D ．221220y x x =-+-【变式训练1】1.在平面直角坐标系中，先将抛物线关于轴作轴对称变换，再将所得的抛物线关于轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ）A ．B ．C ．D ．【规律方法】掌握抛物线的四种对称方式，理解公式的推导过程。

抛物线平移、对称变换专题抛物线平移、对称变换学习目标：1.抛物线平移顶点，与坐标系交点关系2.利用对称性求点的坐标知识框架:【1】抛物线的平移变换只改变抛物线的顶点位置，而不改变抛物线的开口方向与开口大小。

【2】求抛物线y ax2 bx c（ a 0）沿坐标轴平移后的解析式，一般可先将其配方成顶点式y ax h2 k （a 0），然后利用抛物线平移变换的有关规律将原顶点坐标改变成平移后的新顶点坐标即可。

抛物线平移变换的规律是：左加右减（在括号），上加下减（在末梢）。

【3】抛物线绕其顶点旋转180°只改变抛物线的开口方向，而不改变抛物线的开口大小及顶点位置【4】求抛物线y ax2 bx c ( a 0 )绕其顶点旋转180°后的解析式，同样可先将其配方成顶点式y ax h2k ( a 0)，然后将二次项系数直接改变成其相反数即可。

【5】⑴抛物线沿y轴翻折只改变抛物线的顶点位置，而不改变抛物线的开口方向及开口大小。

⑵抛物线沿x轴翻折将同时改变抛物线的开口方向及顶点位置，但抛物线的开口大小不变。

【6】求抛物线y ax2 bx c( a 0 )沿某条坐标轴翻折后的解析式，首先仍应将其配方成顶点式y a x h 2 k ( a 0)，然后再根据翻折的方向来确定新抛物线的解析式若是沿y轴翻折，则只需将其顶点坐标改变成翻折后的新顶点坐标即可；若是沿x轴翻折，则除了要将顶点坐标改变成翻折后的新顶点坐标外，还需将二次系数改变成其相反数。

真题汇编:第一部分（选择题）（2013-2014海淀）二次函数y 2X2+I的图象如图所示，将其绕坐标原点O旋转180o，则旋转后的抛物线的解析式为（)A. y 2x2 1Br 2 , y 2x 1•C・y 2x2Dr 2 ,y 2x 1 •【方法总结】（2015-2016北师大实验二龙路中学）将抛物线y 2x2向左平移1个单位长度，再向上平移3个单位长度得到的抛物线解析式是（）•A • y 2（X 1）2 3B • y 2（x 1）2 3【方法总结】（2015-2016北京三中）将抛物线y 2x2 4绕顶点旋转180 ，则旋转后的抛物线的解析式为( ).A. y 2x2 4 B・y 2x2 4 C . y 2x2 4D. y 2x2【方法总结】（2015-2016北京市昌平第三中学）把抛物线y=2x2-3沿x轴翻折，所得的抛物线是（）2 2 2 2A.y= —2x -3B. 一y = 2x -3C. y = 2x + 3D. y = —2x +3【方法总结】（2015-2016北京三帆中学）二次函数y 3x2+1的图象如图所示，将其沿x轴翻折后得到的抛物线的解析式为*y A. y 3x2 1 B. y 3x2C・y 3x2 1 c 2 ‘y 3x 1【方法总结】丰台区2017-2018如图，在平面直角坐标系中，抛物线y 1x2经过平移得到抛物线y 2x2 2x，其对称轴与两段抛物线所围成的阴影部分的面积是（）B. 4C. 8D. 16【方法总结】第二部分（填空题）海淀区2017- 2018y 2x2平移后经过点A(0,3) , B(2,3),求平移后的抛物线的表达式.【方法总结】（2013-2014海淀）已知点P（ -1 , m在二次函数y x2 1的图象上，贝M m的值为_______________ ；平移此二次函数的图象，使点P与坐标原点重合，则平移后的函数图象所对应的解析式为___________ . ________【方法总结】（2015-2016年北京市第三^一中学）抛物线图像y 2x2经过平移得到抛物线图像y 2x2 4x 5，平移方法是_______【方法总结】朝阳区2015-20 1 6如图，抛物线y=-|x2通过平移得到抛物线m,抛物线m经过点B （6,0）和O （0, 0）,它的顶点为A，以O为圆心，OA 为半径作圆，在第四象限内与抛物线y=-9x2交于点C，连接AC，则图中阴影部分的面积为【方法总结】丰台区2014- 2015如图O的半径为2, Ci是函数的12i 2y —x的图象，C2是函数的y —x的图象，C3是函数的y x的图2 2象，则阴影部分的面积是________【方法总结】（2013-2014东城）二次函数y ax2bx c的图象与x轴交于点A (-1, 0 ),与y轴交于点C (0,-5),且经过点D (3, -8).(1)求此二次函数的解析式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在原点处，并写出平移后抛物线的解析式.【方法总结】(2016-2017北京四十四中初三上期中)抛物线y 2x2向上平移后经过点A(0,3)，求平移后的抛物线的表达式.【方法总结】(2016-2017北京西城铁路第二中学初三上期中) 如图，一段抛物线：y x(x 2)(0W x< 2)，记为C，它与x轴交于点O, A;将C1绕点A旋转180° 得G ,交x 轴于点A ;将C2绕点A旋转180°得G,交x轴于点A;•••，女口此进行下去，直至得G o.(1)请写出抛物线C2的解析式：____________________ ；(2)若P (19, a)在第10段抛物线C。

二次函数专题训练（平移、旋转、轴对称变换）一、二次函数图象的平移、旋转（只研究中心对称）、轴对称变换1、抛物线的平移变换：一般都是在顶点式的情况下进行的。

抛物线的上下平移：___________________y=a（x-h）2+k y=a（x-h）2+k ± m抛物线的左右平移：___________________y=a（x-h）2+k y=a（x-h ± m）2+k练习：（ 1）函数图象沿 y 轴向下平移 2 个单位，再沿 x 轴向右平移 3个单位，得到函数______________ 的图象。

（2）抛物线y x2 2x 5向左平移3个单位，再向下平移 6 个单位，所得抛物线的解析式是。

2、抛物线的旋转变换（只研究中心对称）：一般都是在顶点式的情况下进行的。

1）将抛物线绕其顶点旋转180 （即两条抛物线关于其顶点成中心对称）22y a x h k 关于顶点对称后，得到的解析式是 y a x h k 。

（2）将抛物线绕原点旋转180 （即两条抛物线关于原点成中心对称）22y a x h k 关于原点对称后，得到的解析式是 y a x h k 。

练（1）抛物线y 2x2 4x 6 绕其顶点旋转180 后，所得抛物线的解析式是（2）将抛物线y＝x2＋1绕原点O旋转180°，则旋转后抛物线的解析式为（）22 2 2A．y＝－x2B．y＝－x2＋1 C．y＝x2－1 D．y＝－x2－13、抛物线的轴对称变换：关于 x 轴对称y ax2 bx c关于 x轴对称后，得到的解析式是 y ax2 bx c ；22y a x h k 关于 x 轴对称后，得到的解析式是 y a x h k ；关于y 轴对称22 y ax2 bx c关于y 轴对称后，得到的解析式是 y ax2 bx c；22y a x h k 关于y 轴对称后，得到的解析式是y a x h k ；练习：已知抛物线C1：y （x 2）2 3 （1）抛物线C2与抛物线C1关于y 轴对称，则抛物线C2的解析式为2）抛物线C3与抛物线C1关于x 轴对称，则抛物线 C 3的解析式为总结：根据平移、旋转、轴对称的性质，显然无论作何种变换，抛物线的形状一定不会发生变化，因此 a 永远不变。