高考总复习基础知识:三角函数.pdf
- 格式:pdf
- 大小:72.14 KB
- 文档页数:7


高考三角函数知识点总结一、基本概念和性质1.弧度制:单位圆上的弧所对应的圆心角的大小定义为该弧的弧度。
1弧度等于圆周的1/2π。
2. 三角函数:正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。
3.三角恒等式:包括同角三角恒等式、余角三角恒等式、反三角函数同角恒等式等。
4.周期性:正弦函数、余弦函数、正割函数和余割函数的周期都是2π;正切函数和余切函数的周期是π。
二、基本关系式1.正弦函数:在直角三角形中,正弦函数是指对于一个锐角三角形,三角形的对边和斜边的比值。
- sin(x) = a / c,其中a是对边,c是斜边。
- sin(x) = y / r,其中y是斜边在y轴上的投影,r是半径。
2.余弦函数:在直角三角形中,余弦函数是指对于一个锐角三角形,三角形的邻边和斜边的比值。
- cos(x) = b / c,其中b是邻边,c是斜边。
- cos(x) = x / r,其中x是斜边在x轴上的投影,r是半径。
3.正切函数:在直角三角形中,正切函数是指对于一个锐角三角形,三角形的对边和邻边的比值。
- tan(x) = a / b,其中a是对边,b是邻边。
- tan(x) = y / x,其中y是斜边在y轴上的投影,x是斜边在x轴上的投影。
4.余切函数:余切函数是正切函数的倒数。
- cot(x) = 1 / tan(x)。
5.正割函数:在直角三角形中,正割函数是指对于一个锐角三角形,三角形的斜边和邻边的比值的倒数。
- sec(x) = 1 / cos(x)。
6.余割函数:在直角三角形中,余割函数是指对于一个锐角三角形,三角形的斜边和对边的比值的倒数。
- csc(x) = 1 / sin(x)。
三、平面内角与弧度制之间的关系1.弧度制与度数之间的转换:-弧度=度数×π/180-度数=弧度×180/π2.弧度制下的角的性质:-一个圆上的圆心角的弧度数等于该弧所对应的弧的弧度数。

专题五三角函数与解三角形5.1三角函数的概念、同角三角函数的基本关系及诱导公式考点三角函数的概念、同角三角函数的基本关系及诱导公式1.(2022全国甲理,8,5分)沈括的《梦溪笔谈》是中国古代科技史上的杰作,其中收录了计算圆弧长度的“会圆术”.如图,AB是以O为圆心,OA为半径的圆弧,C是AB的中点,D在AB上,CD⊥AB.“会圆术”给出AB的弧长的近似值s的计算公式:s=AB+CD 2OA.当OA=2,∠AOB=60°时,s=( )A.11−3√32B.11−4√32C.9−3√32D.9−4√32答案 B 连接OC,如图.∵C是AB的中点,OA=OB=2,∴OC⊥AB.又∵CD⊥AB,∴D,C,O三点共线.∵∠AOB=60°,∴AB=2,OC=√3,CD=2-√3,∴s=2+(2−√3)22=11−4√32,故选B.2.(2019北京文,8,5分)如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为()A.4β+4cos βB.4β+4sin βC.2β+2cos βD.2β+2sin β答案 B 本题主要考查扇形面积、三角形面积公式及应用;主要考查学生的推理论证能力和运算求解能力;考查的核心素养是数学运算.由圆的性质易知,当|PA|=|PB|时,阴影部分的面积最大,其面积为△PAB 的面积与弓形的面积之和. 作PD ⊥AB 于D 点,由∠APB=β,知∠DOB=β(O 为圆心).所以|OD|=2cos β,|PD|=2+2cos β,|AB|=4sin β.所以S △PAB =12·|AB|·|PD|=4sin β(1+cos β).S 弓形=S 扇形OAB -S △OAB =12·2β·22-12·4sin β·2cos β=4β-4sin β· cos β.故阴影部分的面积为S △PAB +S 弓形=4sin β+4sin βcos β+4β-4sin βcos β=4β+4sin β.故选B.思路分析 本题阴影部分由一个三角形与一个弓形构成,当β确定时,弓形面积是确定的,故三角形面积最大时,阴影部分面积最大.3.(2014课标Ⅰ文,2,5分)若tan α>0,则( ) A.sin α>0 B.cos α>0 C.sin 2α>0 D.cos 2α>0答案 C 由tan α>0得α是第一或第三象限角,若α是第三象限角,则A,B 错;由sin 2α=2sin αcos α知sin 2α>0,C 正确;α取π3时,cos 2α=2cos 2α-1=2×(12)2-1=-12<0,D 错.故选C.评析 本题考查三角函数值的符号,判定时可运用基本知识、恒等变形及特殊值等多种方法,具有一定的灵活性.4.(2014大纲全国文,2,5分)已知角α的终边经过点(-4,3),则cos α=( ) A.45B.35C.-35D.-45答案 D 由三角函数的定义知cos α=√(−4)+3=-45.故选D.5.(2015福建文,6,5分)若sin α=-513,且α为第四象限角,则tan α的值等于( ) A.125 B.-125 C.512 D.-512答案 D ∵sin α=-513,α为第四象限角,∴cos α=√1−sin 2α=1213,∴tan α=sinαcosα=-512.故选D. 6.(2014大纲全国理,3,5分)设a=sin 33°,b=cos 55°,c=tan 35°,则( ) A.a>b>c B.b>c>a C.c>b>a D.c>a>b 答案 C ∵b=cos 55°=sin 35°>sin 33°=a,∴b>a.又∵c=tan 35°=sin35°cos35°>sin 35°=cos 55°=b,∴c>b.∴c>b>a.故选C.7.(2013浙江理,6,5分)已知α∈R,sin α+2cos α=√102,则tan 2α=( )A.43B.34C.-34D.-43答案 C (sin α+2cos α)2=52,展开得3cos 2α+4sin αcos α=32,再由二倍角公式得32cos 2α+2sin 2α=0,故tan 2α=sin2αcos2α=-322=-34,选C.评析 本题考查同角三角函数的基本关系式和三角恒等变换,考查转化与化归思想,考查学生灵活应用公式的能力和运算求解能力.三角函数求值问题关键在于观察角与角之间的关系和三角函数名之间的关系. 8.(2013大纲全国文,2,5分)已知α是第二象限角,sin α=513,则cos α=( ) A.-1213 B.-513 C.513 D.1213答案 A ∵α是第二象限角,∴cos α<0. ∴cos α=-√1−sin 2α=-1213.故选A. 评析 本题考查三角函数值在各象限的符号,同角三角函数关系,属容易题. 9.(2013广东文,4,5分)已知sin (5π2+α)=15,那么cos α=( ) A.-25B.-15C.15D.25答案 C ∵sin (5π2+α)=sin (π2+α)=cos α,∴cos α=15.故选C. 10.(2017北京文,9,5分)在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于y 轴对称.若sin α=13,则sin β= . 答案13 解析 本题考查三角函数的诱导公式.由角α与角β的终边关于y 轴对称,可得β=(2k+1)π-α,k ∈Z,∵sin α=13,∴sin β=sin[(2k+1)π-α]=sin α=13.11.(2011江西文,14,5分)已知角θ的顶点为坐标原点,始边为x 轴的正半轴.若P(4,y)是角θ终边上一点,且sin θ=-2√55,则y= . 答案 -8解析 P(4,y)是角θ终边上一点,由三角函数的定义知sin θ=√16+y ,又sin θ=-2√55,∴√16+y =-2√55,解得y=-8.评析 本题主要考查任意角三角函数的定义,考查运算求解能力,由题意得√16+y 2=-2√55是本题求解的关键.12.(2016四川文,11,5分)sin 750°= . 答案12解析 sin 750°=sin(720°+30°)=sin 30°=12. 解后反思 利用诱导公式把大角化为小角. 评析 本题考查了三角函数的诱导公式.13.(2013课标Ⅱ理,15,5分)设θ为第二象限角,若tan (θ+π4)=12,则sin θ+cos θ= . 答案 -√105解析 tan θ=tan [(θ+π4)−π4]=12−11+12=-13,∴sin θ=-13cos θ,将其代入sin 2θ+cos 2θ=1得109cos 2θ=1,∴cos 2θ=910,又易知cos θ<0,∴cos θ=-310√10,∴sin θ=√1010,故sin θ+cos θ=-√105.。



高考数学-三角函数专题复习三角函数专题考点例题解析】考点1.求值1、求sin330°、tan690°、sin585°的值。
解:利用三角函数的周期性和对称性,可得:sin330°=sin(360°-30°)=sin30°=1/2tan690°=tan(720°-30°)=tan30°=1/√3sin585°=sin(540°+45°)=sin45°=√2/22、已知角α为第三象限角,求sin(α+π/2)的值。
解:由于α为第三象限角,所以sinα<0,cosα<0.又因为sin(α+π/2)=cosα,所以sin(α+π/2)<0.3、已知sinθ+cosθ=5/3,cosθ-sinθ=2,求sin2θ的值。
解:将sinθ+cosθ和cosθ-sinθ相加,可得cosθ+cosθ=5/3+2=11/3,即cosθ=11/6.将cosθ-sinθ和sinθ+cosθ相减,可得2sinθ=-1/6,即sinθ=-1/12.代入sin2θ=2sinθcosθ的公式,可得sin2θ=-11/72.4、已知si n(π/4-α)=2/√5,求cosα的值。
解:sin(π/4-α)=sinπ/4cosα-cosπ/4sinα=2/√5,代入cosπ/4=√2/2和sinπ/4=√2/2,可得cosα=1/√10.5、已知f(cosx)=cos3x,求f(sin30°)的值。
解:将x=π/6代入f(cosx)=cos3x,可得f(cosπ/6)=cos(3π/6)=cosπ=-1.又因为sin30°=cosπ/6,所以f(sin30°)=-1.6、已知tanα=15π/22,求cos(π/2-α)的值。
解:tanα=15π/22,所以α为第三象限角,cos(π/2-α)=sinα>0.由tanα=sinα/cosα,可得cosα=15/√466,代入sin^2α+cos^2α=1,可得sinα=7/√466,最终可得cos(π/2-α)=7/15.7、已知tan(π/4+x)=2tan(π/4-x),求cos2x的值。
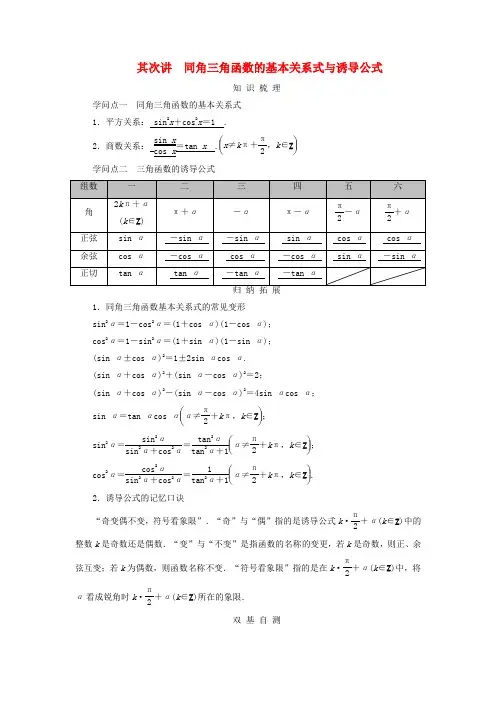
其次讲 同角三角函数的基本关系式与诱导公式知 识 梳 理学问点一 同角三角函数的基本关系式 1.平方关系: sin 2x +cos 2x =1 .2.商数关系: sin x cos x =tan x .⎝ ⎛⎭⎪⎫x ≠k π+π2,k ∈Z 学问点二 三角函数的诱导公式1.同角三角函数基本关系式的常见变形 sin 2α=1-cos 2α=(1+cos α)(1-cos α); cos 2α=1-sin 2α=(1+sin α)(1-sin α); (sin α±cos α)2=1±2sin αcos α. (sin α+cos α)2+(sin α-cos α)2=2;(sin α+cos α)2-(sin α-cos α)2=4sin αcos α; sin α=tan αcos α⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z ; sin 2α=sin 2αsin 2α+cos 2α=tan 2αtan 2α+1⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z ; cos 2α=cos 2αsin 2α+cos 2α=1tan 2α+1⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z .2.诱导公式的记忆口诀“奇变偶不变,符号看象限”.“奇”与“偶”指的是诱导公式k ·π2+α(k ∈Z )中的整数k 是奇数还是偶数.“变”与“不变”是指函数的名称的变更,若k 是奇数,则正、余弦互变;若k 为偶数,则函数名称不变.“符号看象限”指的是在k ·π2+α(k ∈Z )中,将α看成锐角时k ·π2+α(k ∈Z )所在的象限.双 基 自 测题组一 走出误区1.推断下列结论是否正确(请在括号中打“√”或“×”) (1)sin (π+α)=-sin α成立的条件是α为锐角.( × ) (2)若α∈R ,则tan α=sin αcos α恒成立.( × )(3)若α,β为锐角,则sin 2α+cos 2β=1.( × ) (4)若sin(k π-α)=13(k ∈Z ),则sin α=13.( × )[解析] (1)依据诱导公式知α为随意角.(2)cos α≠0时才成立.(3)依据同角三角函数的基本关系式知当α,β为同角时才正确.(4)sin(k π-α)=±sin α,∴sin α=±13. 题组二 走进教材2.(必修1P 184练习T1改编)若α是钝角且sin α=13,则tan α=( A )A .-24B .24C .-22D .22[解析] 由已知利用同角三角函数基本关系式即可求解.因为α是钝角且sin α=13,所以cos α=-1-sin 2α=-223,则tan α=sin αcos α=-24.故选A .3.(必修1P 186T15改编)已知tan α=3,则sin π-α+2cos π+αsin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2+α=( B )A .-12B .14C .54D .12[解析] 利用诱导公式、同角三角函数的基本关系式求得正确答案.sin π-α+2cos π+αsin ⎝ ⎛⎭⎪⎫π2+α+cos ⎝ ⎛⎭⎪⎫3π2+α=sin α-2cos αcos α+sin α=tan α-21+tan α=3-21+3=14.故选B .4.(必修1P 186T16改编)化简cos α1-sin α1+sin α+sin α1-cos α1+cos α ⎝⎛⎭⎪⎫π<α<3π2得( A )A .sin α+cos α-2B .2-sin α-cos αC .sin α-cos αD .cos α-sin α[解析] 原式=cos α1-sin α2cos 2α+sin α1-cos α2sin 2α,∵π<α<32π,∴cos α<0,sin α<0.∴原式=-(1-sin α)-(1-cos α)=sin α+cos α-2. 题组三 走向高考5.(2024·全国卷Ⅰ,7)tan 255°=( D ) A .-2- 3 B .-2+ 3 C .2- 3D .2+ 3[解析] 由正切函数的周期性可知,tan 255°=tan(180°+75°)=tan 75°=tan(30°+45°)=33+11-33=2+3,故选D .另:tan 255°=tan 75°>tan 60°=3,∴选D .6.(2015·福建)若sin α=-513,且α为第四象限角,则tan α的值等于( D )A .125B .-125C .512D .-512[解析] 因为sin α=-513,且α为第四象限角,所以cos α=1213,所以tan α=-512,故选D .7.(2024·全国乙文,14,5分)若θ∈⎝ ⎛⎭⎪⎫0,π2,tan θ=13,则sin θ-cos θ= -105. [解析] 由tan θ=13,可得sin θcos θ=13,又sin 2θ+cos 2θ=1,θ∈⎝⎛⎭⎪⎫0,π2,所以sin θ=1010,cos θ=31010, 所以sin θ-cos θ=1010-31010=-105.。

三角公式汇总一、任意角的三角函数在角α的终边上任取..一点),(y x P ,记:22y x r +=, 正弦:r y =αsin 余弦:r x =αcos 正切:xy=αtan 注:我们还可以用单位圆中的有向线段表示任意角的三角函数:如图,与单位圆有关的有向..线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线。
二、同角三角函数的基本关系式平方关系:1cos sin 22=+αα 商数关系:αααcos sin tan =三、诱导公式四、和角公式和差角公式βαβαβαsin cos cos sin )sin(⋅+⋅=+ βαβαβαsin cos cos sin )sin(⋅-⋅=- βαβαβαsin sin cos cos )cos(⋅-⋅=+ βαβαβαsin sin cos cos )cos(⋅+⋅=- βαβαβαtan tan 1tan tan )tan(⋅-+=+βαβαβαtan tan 1tan tan )tan(⋅+-=-五、二倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-= )(*ααα2tan 1tan 22tan -=二倍角的余弦公式)(*有以下常用变形:(规律:降次扩角,升次缩角)六、辅助角公式sin cos )a x b x x φ±=± 其中: 22sin b a b +=ϕ,22cos b a a +=ϕ,ab=ϕtan七、正弦函数、余弦函数和正切函数的图象与性质:sin y x =cos y x = tan y x =图象定义域R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时,max 1y =;当22x k ππ=-()k ∈Z 时,min 1y =-.当()2x k k π=∈Z 时,max 1y =;当2x k ππ=+()k ∈Z 时,min 1y =-.既无最大值也无最小值周期性 2π2ππ奇偶性奇函数偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k ∈Z 上是减函数.在[]()2,2k k k πππ-∈Z 上是增函数;在[]2,2k k πππ+()k ∈Z 上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭()k ∈Z 上是增函数.对称性对称中心()(),0k k π∈Z对称轴()2x k k ππ=+∈Z函 数 性 质八、正弦定理R CcB b A a 2sin sin sin ===(R 为ABC ∆外接圆半径) 九、余弦定理A bc c b a cos 2222⋅-+=B ac c a b cos 2222⋅-+=C ab b a c cos 2222⋅-+=十、三角形的面积公式B ca A bcC ab S ABC sin 21sin 21sin 21===∆(两边一夹角) r cb a S ABC ⋅++=∆2(r 为ABC ∆内切圆半径)。

三角函数公式一、三角函数的和差公式1、cos(A-B)=cosAcosB+sinAsinB2、cos(A+B)=cosAcosB-sinAsinB3、sin(A+B)=sinAcosB+cosAsinB4、sin (A-B)= sinAcosB-cosAsinB5、tan(A+B)=tan A+tanB 1tan AtanB-6、tan(A-B)=tan A-tanB 1tan AtanB+二、倍角公式7、sin2A= 2sinAcosB8、cos2A=cos A-sin A (变形形式cos2A=1-2sin A ;cos2A=2cos A-1)22229、tan2A=22tan A 1tan A-三、积化和差公式10、sinAcosB=[sin(A+B) +sin (A-B)]12证:右=[sin(A+B) +sin (A-B)]12=[ (sinAcosB+cosAsinB) + (sinAcosB-cosAsinB)]12 = sinAcosB=左11、cosAsinB=[sin(A+B) -sin (A-B)]12证:右=[sin(A+B) -sin (A-B)]12=[ (sinAcosB+cosAsinB) - (sinAcosB-cosAsinB)]12 = cosAsinB =左12、cosAcosB=[cos(A+B)+cos (A-B)]12证:右=[cos(A+B)+cos (A-B)]12=[ (cosAcosB-sinAsinB)+ (cosAcosB+sinAsinB)]12 = cosAcosB =左13、sinAsinB=[cos(A-B)-cos (A+B)]12证:右=[cos(A+B)+cos (A-B)]12=[ (cosAcosB+sinAsinB)+ (cosAcosB-sinAsinB)]12 = sinAsinB =左四、和差化积公式14、sinA+sinB=2sin cos A B 2+A B 2-证:令X=,Y=,则A=X+Y ,B=X-Y A B 2+A B 2-左= sinA+sinB= sin(X+Y)+sin(X-Y)=( sinXcosY+cosXsinY)+( sinXcosY-cosXsinY)=2 sinXcosY=2sin cos =右A B 2+A B 2-15、sinA-sinB=2sin cos A B 2-A B 2+证:左= sinA-sinB= sinA+sin(-B)= 2sin cos =右A+(B)2-A-(-B)216、cosA+cosB=2cos cos A B 2+A B 2-证:令X=,Y=,则A=X+Y ,B=X-Y A B 2+A B 2-左= cosA+cosB = cos(X+Y)+cos(X-Y)=( cosXcosY-sinXsinY)+( cosXcosY+sinXsinY)=2cosXcosY=2cos cos =右A B 2+A B 2-17、cosA-cosB=-2sin sin A B 2+A B 2-证:令X=,Y=,则A=X+Y ,B=X-Y A B 2+A B 2-左= cosA-cosB = cos(X+Y)-cos(X-Y)=( cosXcosY-sinXsinY)-( cosXcosY+sinXsinY)=-2sinXsinY=-2sin sin =右A B 2+A B 2-补充:18、sin2A=22tan A 1tan A+证:左=22222sin A22tan A 2sin A cos A sin 2A cos A sin 2A=sin A 1tan A sin A cos A 11cos A ⋅====+++右19、cos2A=221tan A 1tan A-+证:左=2222222222sin A 11tan A sin A cos A cos 2A cos A cos 2A=sin A 1tan A sin A cos A 11cos A---====+++右五、万能公式令t=tan ,则A2sinA=(公式18的变形);221tt +cosA=(公式19的变形);2211t t -+tanA=(公式9的变形)。

新高考数学复习基础知识专题讲义 知识点05 三角函数定义及同角三角函数知识理解 一.任意角 (1)角的概念的推广①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角.(2)终边相同的角:终边与角α相同的角可写成α+k ·360°(k ∈Z). (3)弧度制①1弧度的角:长度等于半径长的弧所对的圆心角叫做1弧度的角.②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,|α|=lr ,l 是以角α作为圆心角时所对圆弧的长,r 为半径.③弧度与角度的换算:360°=2π rad ;180°=π rad ;1°=π180 rad ;1 rad =180π度. 二.任意角的三角函数1.定义:在平面直角坐标系中,设α的终边上任意一点P 的坐标是(x ,y ),它与原点的距离是r (r =x 2+y 2>0).则sin α=y r ,cos α=x r ,tan α=yx (x ≠0).2.三角函数在每个象限的正负如下表:三.同角三角函数的基本关系(1)平方关系:sin 2α+cos 2α=1(2)商数关系:sin αcos α=tan α⎝⎛⎭⎫α≠π2+k π,k ∈Z . 四.同角三角函数基本关系式的变形(1)sin 2α+cos 2α=1的变形公式:sin 2α=1-cos 2α;cos 2α=1-sin 2α; (2)tan α=sin αcos α的变形公式:sin α=cos_αtan_α;cos α=sin αtan α.考向一 角度制与弧度制的转换【例1-1】(2020·全国课时练习)填表(弧度数用含π的代数式表示),并在平面直角坐标系中作出角的终边.【答案】填表见解析,作图见解析 【解析】如表,如图:考向分析对应的角的终边分别为图中的射线OA ,OB ,OC ,OD ,OE ,OF ,OG ,OH ,OI. 【例1-2】(2020·全国课时练习)把下列各弧度化为角度. (1)12π;(2)53π;(3)310π;(4)8π;(5)32π-;(6)56π-. 【答案】(1)15︒;(2)300︒;(3)54︒;(4)22.5︒;(5)270︒-;(6)150︒-.【解析】(1)1801512ππ︒︒⨯=;(2)51803003ππ︒︒⨯=;(3)18054310ππ︒︒⨯=;(4)28180 2.5ππ︒︒⨯=;(5)31802702ππ︒︒-⨯=-;(6)51801506ππ︒︒-⨯=-.【例1-3】(2019·全国高三专题练习)将-1485°改写成2k π+α(0≤α<π,k ∈Z)的形式是( ) A .-8π+4πB .-10π-4πC .-8π+74πD .-10π+74π 【答案】D【解析】﹣1485°=﹣1800°+315°=﹣10π+74π.故选D【举一反三】1.(2020·全国课时练习)把下列角度化成弧度:(1)36︒; (2)150︒-; (3)1095︒; (4)1440︒. 【答案】(1)5π(2)56π-(3)7312π(4)8π 【解析】(1)361805ππ︒⨯=; (2)51501806ππ-︒⨯=-; (3)73109518012ππ︒⨯=; (4)14408180ππ︒⨯=. 2.(2020·全国课时练习)将下列角度与弧度进行互化. (1)20°;(2)-15°;(3)712π(4)-115π. 【答案】(1)20°=9π;(2)-15°=-12π;(3)712π=105°;(4)-115π=-396°.【解析】(1)20°=20180π=9π. (2)-15°=-15180π=-12π.(3)712π=712×180°=105°. (4)-115π=-115×180°=-396°.3.(2020·全国高三专题练习)把−1125°化成α+2k π(0≤α<2π,k ∈Z)的形式是( ) A .−π4−6πB .7π4−6πC .−π4−8πD .7π4−8π【答案】D【解析】−1125°=−1440°+315°=−8π+7π4,故选D.4.(2019·全国高三专题练习)将-1485°化成α+2k π(0≤α<2π,k ∈Z)的形式是( ) A .-4π-8πB .74π-8πC .4π-10πD .74π-10π【答案】D【解析】由题意,可知-1485°=-5×360°+315°,又π=180°,则315°=74π, 故-1485°化成α+2k π(0≤α<2π,k ∈Z)的形式是74π-10π. 考向二 三角函数定义【例2】(1)(2020·云南)已知角α的终边经过点34(,)55P -,则sin α等于( ) A .45B .35C .43-D .34- (2)(2020·广东)已知角θ的终边上一点(4,3)(0)P a a a ≠,则sin θ=( ) A .45B .35C .45±D .35± 【答案】(1)A (2)D【解析】(1)因为角α的终边经过点34(,)55P -,所以x 34,,155y r =-==,所以4sin 5y r α==,故选:A(2)5OP a == 由三角函数的定义可得333sin 55a a OP a θ===±故选:D 【举一反三】1.(2020·北京)在平面直角坐标系xOy 中,角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,终边经过点(3,4)P ,那么sin α的值是( ) A .35B .34C .45D .43 【答案】C【解析】由已知5OP ==,所以4sin 5α.故选:C . 15.(2020·商南县高级中学)角α的终边过点()3,4P a ,若3cos 5α=-,则a 的值为( ) A .1B .1-C .±1D .5± 【答案】B【解析】由条件可知r OP ==, 由三角函数的定义可知3cos 5x r α===-,0a <,解得:1a =-.故选:B 3.(2019·吉林高三月考(文))若点cos ,sin36ππ⎛⎫⎪⎝⎭在角α的终边上,则tan α的值是( )A .-1B .1C .【答案】B【解析】据题意,得1sin62tan 11cos32παπ===.故选:B.考向三 三角函数正负判断【例3】(1)(2020·山东高三专题练习)已知cos tan 0θθ⋅>,那么θ是( ) A .第一、二象限角B .第二、三象限角C .第三、四象限角D .第一、四象限角(2)(2020·山东高三专题练习)若α是第二象限角,则点()sin ,cos P αα在 ( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】(1)A (2)D【解析】(1)由cos tan 0θθ⋅>可知cos ,tan θθ同号,即cos tan =sin 0θθθ⋅>,从而θ为第一、二象限角,故选:A(2)因为α是第二象限角,所以sin 0,cos 0αα><,所以点()sin ,cos P αα在第四象限,故选D【举一反三】1.(2019·浙江高三专题练习)已知 sin 0θ>且cos 0θ<,则角的终边所在的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】依据题设及三角函数的定义可知角θ终边上的点的横坐标小于零,纵坐标大于零, 所以终边在第二象限,故选B.2.(2020·全国高三专题练习)若sin tan 0αα<,且cos 0tan αα<,则角α是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角 【答案】 C【解析】2sin sin tan 0cos αααα=<,cos 0α∴<,又2cos cos 0tan sin αααα=<,则sin 0α<. 因此,角α为第三象限角.故选:C.3.(2020·全国高三专题练习)已知sin cos 0θθ<,且cos cos θθ=,则角θ是( ) A .第一象限角B .第二象限角C .第三象限角D .第四象限角 【答案】D【解析】由cos cos θθ=,可知cos 0θ≥,结合sin cos 0θθ<,得sin 0,cos 0θθ<>, 所以角θ是第四象限角,故选:D4.(多选)(2020·全国高三专题练习)对于①sin 0θ>,②sin 0θ<,③cos 0θ>,④cos 0θ<,⑤tan 0θ>,⑥tan 0θ<,则θ为第二象限角的充要条件为( ) A .①③B .①④C .④⑥D .②⑤ 【答案】BC【解析】若θ为第二象限角,则sin 0θ>,cos 0θ<,tan 0θ<.所以,θ为第二象限角sin 0cos 0θθ>⎧⇔⎨<⎩或sin 0tan 0θθ>⎧⎨<⎩或cos 0tan 0θθ<⎧⎨<⎩.故选:BC.考向四 同角三角公式【例4】(1)(2019·全国高三专题练习)已知α是第四象限角,cos α=1213,则sin α等于( ) A .513B .-513 C .512D .-512(2)(2020·江西景德镇一中)已知2tan 3α=,且2απ<<π,则cos α=( )A .13-B .13.13-D .13【答案】(1)B (2)A【解析】由条件知α是第四象限角,所以sin 0α<,即sin α===513-. 故选:B . (2)2tan 03α=>且2απ<<π,32ππα∴<<,cos 0α∴<, 由22sin 2tan cos 3sin cos 1ααααα⎧==⎪⎨⎪+=⎩得:cos 13α=-故选:A .【举一反三】1.(2020·海拉尔市蒙古族中学高三学业考试)已知α为第四象限的角,且3cos 5α=,则tan α的值为( ) A .34B .34-C .43D .43-【答案】D【解析】α为第四象限的角,且3cos 5α=,4sin 5α∴===-.4sin 45tan 3cos 35ααα-∴===-.故选:D .2.(2019·北京海淀·101中学高三月考)已知3,22ππα⎛⎫∈ ⎪⎝⎭,且tan α=那么sin α=( )A .-.D【答案】B【解析】因为3(,)22ππα∈,sin tan 0cos ααα==>,故3(,)2παπ∈, sin αα=,又22sin cos 1αα+=,解得:sin α=故选:B 3.已知tan α=43,且α是第三象限角,求sin α,cos α的值.【答案】见解析【解析】由tan α=sin αcos α=43,得sin α=43cos α①又sin 2α+cos 2α=1②由①②得169cos 2α+cos 2α=1,即cos 2α=925.又α是第三象限角,∴cos α=-35,sin α=43cos α=-45.考向五 弦的齐次【例5】(1)已知tan α=2,则sin α+cos αsin α-cos α的值为.(2)(2020·固原市五原中学高三)已知tan 2θ=,则2sin sin cos 2θθθ+-= 【答案】(1)3(2)45-(1)原式=tan α+1tan α-1=2+12-1=3. (2)因为22sin +cos 1θθ=,sin tan cos θθθ=所以222sin sin cos 2sin sin cos 2cos θθθθθθθ+-=-+-222222sin sin cos 2cos tan tan 2sin +cos tan +1θθθθθθθθθ-+--+-==42244+15-+-==-故选:D.【举一反三】1.(2020·全国高三专题练习)已知1tan 3α=-,则2cos sin cos ααα-+的值为( ) A .3-B .34-C .43-D .34【答案】A【解析】由1tan 3α=-,得2cos 2232sin cos 1tan 3αααα---===-++.故选:A.2.(2020·福建省武平县第一中学高三月考)已知tan 2θ=,则22sin sin cos 2cos θθθθ+-等于( ) A .43-B .54C .34-D .45【答案】D【解析】222222sin sin cos 2cos sin sin cos 2cos sin cos θθθθθθθθθθ+-+-=+22tan tan 24224tan 1415θθθ+-+-===++. 故选:D3.(2020·西藏拉萨中学高三)1tan 2α=,则sin 2α=( ) A .45-B .35C .45D .35【答案】C【解析】1tan 2α=,2222122sin cos 2tan 42sin 21151()2sin cos tan ααααααα⨯∴====+++.故选:C 4.(2020·江苏南京田家炳高级中学)已知tan 2α=,求:(1)sin 2cos sin cos αααα+-; (2)221sin sin cos 2cos αααα+-.【答案】(1) 4 (2)54【解析】(1)sin 2cos tan 2224sin cos tan 121αααααα+++===--- (2)2222221sin cos sin sin cos 2cos sin sin cos 2cos αααααααααα+=+-+-2222tan 1215tan tan 22224ααα++===+-+- 考向六 sin cos sin cos α±ααα与【例6】(1)(2020·永寿县中学高三开学考试)已知4sin cos 3αα-=,则sin 2α=( ). A .79-B .29-C .29D .79(2)(2020·广东华南师大附中高三月考)已知1sin cos 5αα+=,其中,2παπ⎛⎫∈ ⎪⎝⎭,则tan α=( )A .247B .43-或34-C .34-D .43- 【答案】(1)A (2)D【解析】()2sin cos 17sin 22sin cos 19ααααα--===--.所以选A.(2)由1sin cos 5αα+=,平方可得112sin cos 25αα+=,解得242sin cos 25αα=-, 又由2249(sin cos )sin cos 2sin cos 25αααααα-=+-=,因为,2παπ⎛⎫∈⎪⎝⎭,可得sin cos 0αα->,所以7sin cos 5αα-=,联立方程组1sin cos 57sin cos 5αααα⎧+=⎪⎪⎨⎪-=⎪⎩,解得43sin ,cos 55αα==-,所以sin tan s 43co ααα==-.故选:D.【举一反三】1.(2020·上海市奉贤区曙光中学高三期中)已知7sin cos17αα+=,()0,απ∈,则tanα=________.【答案】158-【解析】依题意7sin cos17αα+=,两边平方得4924012sin cos,2sin cos0289289αααα+==-<,而()0,απ∈,所以sin0,cos0αα><,所以23sin cos17αα-====.由7sin cos1723sin cos17αααα⎧+=⎪⎪⎨⎪-=⎪⎩解得158sin,cos1717αα==-,所以sin15tancos8ααα==-.故答案为:158-2.(2020·四川省南充高级中学高三月考(理))已知1sin cos5θθ+=,(0,)θπ∈,则tanθ=________. 【答案】43-【解析】已知1sin cos5θθ+=,平方得()2221sin cos sin cos2sin cos25θθθθθθ+=++=,得12sin cos25θθ=-,∴()222sin cos sin cos2sin cos125252449θθθθθθ-=+-=+=,(0,)θπ∈,sin0,cos0θθ><,7sin cos 5θθ∴-=,7ta sin cos 1sin cos n 571t n 51a θθθθθθ=-=-+=+,解得4tan 3θ=-. 故答案为:43-考向七 三角函数线运用【例7】(2020·全国高三专题练习)已知点(sin cos ,tan )P ααα-在第一象限,则在[0,2]π内α的取值范围是( ).A .35,,244ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭B .5,,424ππππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭C .353,,2442ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭D .3,,424ππππ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭【答案】B【解析】由已知点(sin cos ,tan )P ααα-在第一象限得:sin cos 0αα->,tan 0α>,即sin cos αα>,tan 0α>,当sin cos αα>,可得52244k k πππαπ+<<+,k Z ∈. 当tan 0α>,可得222k k ππαπ<<+或3222k k πππαπ+<<+,k Z ∈. ∴2242k k πππαπ+<<+或5224k k πππαπ+<<+,k Z ∈. 当0k =时,42ππα<<或54ππα<<. 02απ,∴42ππα<<或54ππα<<.故选:B .【举一反三】1.(2020·全国高三专题练习)已知点()cos ,tan P αα在第二象限,则角α在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】C【解析】点()cos ,tan P αα在第二象限,则cos 0tan 0αα<⎧⎨>⎩,所以角α在第三象限.故选:C2.(2020·海伦市第一中学高三期中(文))已知点()cos sin ,sin cos P αααα+-在第三象限,则α的取值范围是( ). A .()ππ2π,2π42k k k ⎛⎫++∈ ⎪⎝⎭Z B .()3π2π,2ππ4k k k ⎛⎫++∈ ⎪⎝⎭Z C .()3π5π2π,2π44k k k ⎛⎫++∈ ⎪⎝⎭Z D .()5π7π2π,2π44k k k ⎛⎫++∈ ⎪⎝⎭Z【答案】D 【解析】()cos sin ,sin cos P αααα+-在第三象限,cos sin 0sin cos 0αααα+<⎧∴⎨-<⎩,2222sin cos sin 1sin sin 0sin 0αααααα⎧⎧>>-∴⇒⎨⎨<<⎩⎩,21sin 2sin 0αα⎧>⎪∴⎨⎪<⎩,sin α∴<,()5π7π2π,2π44k k k α⎛⎫∴∈++∈ ⎪⎝⎭Z.故选:D. 3.(2020·贵州高三其他模拟)已知点(sin cos ,tan )P ααα-在第一象限,则在[]0,2π内的α的取值范围是( )A .35(,)(,)244ππππB .5(,)(,)424ππππC .353(,)(,)2442ππππD .33(,)(,)244ππππ 【答案】B【解析】由已知点(sin cos ,tan )P ααα-在第一象限得:sin cos 0αα->,tan 0α>,即sin cos αα>,tan 0α>,当sin cos αα>,可得52244k k πππαπ+<<+,k Z ∈.当tan 0α>,可得222k k ππαπ<<+或3222k k πππαπ+<<+,k Z ∈. ∴2242k k πππαπ+<<+或5224k k πππαπ+<<+,k Z ∈. 当0k =时,42ππα<<或54ππα<<.02απ≤≤,∴42ππα<<或54ππα<<.故选:B .1.(2020·重庆西南大学附中高三月考)下列转化结果正确的是( ) A .60化成弧度是rad 6πB .rad 12π化成角度是30 C .1化成弧度是180rad πD .1rad 化成角度是180π⎛⎫⎪⎝⎭【答案】D【解析】由180π=得,对于A 选项:60化成弧度是rad 3π,故A 不正确;对于B 选项:rad 12π化成角度是11801512⨯=,故B 不正确;对于C 选项:1化成弧度是180rad π,故C 错误;对于D 选项:1rad 化成角度是180π⎛⎫⎪⎝⎭,故D 正确,故选:D.2.(2020·天津市静海区大邱庄中学高三月考)下列转化结果错误的是( ) A .30化成弧度是6πB .103π-化成度是600-︒ C .6730'︒化成弧度是27πD .85π化成度是288︒ 【答案】C【解析】30化成弧度是6π,A 正确;103π-化成度是600-︒,B 正确; 6730'︒是367.567.51808ππ︒=⨯=,C 错误;85π化成度是288︒,D 正确.故选:C. 3.(2020·江苏高三专题练习)225-化为弧度为()强化练习A .34πB .74π-C .54π-D .34π- 【答案】C【解析】225225356024ππ=-⋅-=-.故选C 4.(2019·全国高三专题练习)下列结论不正确的是( )A .3πrad =60°B .10°=18πrad C .36°=5πradD .58πrad =115°【答案】D 【解析】 ∵π=180°,∴3πrad =60°正确,10°=18πrad 正确,36°=5πrad 正确,58πrad ==112.5°≠115°,D 不正确.故选D .5.(2020·浙江温州·高二期中)已知角α的终边上有一点()1,2P -,则tan α的值为( ) A .-2B .12-C D .【答案】A 【解析】角α的终边上有一点()1,2P -,2tan 21α-∴==-.故选:A. 6.(2020·江苏镇江·高三期中)已知点51,3tan6P π⎛⎫- ⎪⎝⎭是角θ终边上一点,则cosθ的值为( ) A .12B.12-D. 【答案】C【解析】因为53tan 36π⎛=⨯= ⎝⎭(1,P -,所以1cos 2θ==-,故选:C.7.(2020·河南高三月考(文))已知角α的顶点在坐标原点,始边在x 轴非负半轴上,终边与单位圆交于12P ⎛-⎝⎭,则sin α=( ) A.B .12-C..2【答案】D【解析】由三角函数的定义,sin y α==.故选:D. 8.(2020·北京人大附中高三月考)已知点5π2cos,16P ⎛⎫⎪⎝⎭是角α终边上一点,则sin α=( ) A .12B.2C .12-D.2- 【答案】A【解析】由5πcos62=-,可得点()P , 根据三角函数的定义,可得1sin 2α==.故选:A.9.(2020·浙江高二开学考试)已知角α的终边经过点(2,1)P -,则( )A .sin αB .sin α=C .cos α=D .tan 2α【答案】A【解析】角α的终边经过点(2,1)P -,所以P根据三角函数定义得到:sin 55a α====-,1tan 2α=-;故选A. 10.(2020·开鲁县第一中学高三月考(文))已知角α的终边经过点P (4,-3),则2sin cos αα+的值等于( ) A .25-B .45C .35D .25【答案】A【解析】因为角α的终边过点()4,3,5P r OP -==,所以利用三角函数的定义, 求得34,cos 55sin αα=-=,3422cos 2555sin αα∴+=-⨯+=-,故选A. 11.(2020·宁夏银川二中高三其他模拟)如果角α的终边过点(2sin30,2cos30)︒-︒,则sin α的值等于( )A .12B .12-C.D.-【答案】C【解析】由题意()(2sin30,2cos301,︒-︒= ,点(1,到原点的距离2r ==,由定义知sin 2y r α==-故选:C . 12.(2020·扶风县法门高中高三月考(文))已知α的值是( )A .3B .3-C .1D .12- 【答案】Ccos 2sin cos sin cos ααααα+=+, 因为α为第二象限角,所以sin 0,cos 0αα><,所以cos 2sin 2sin cos 211sin cos sin cos αααααααα-+=+=-=.故选:C. 13.(2020·安徽省蚌埠第三中学高一开学考试)已知点(tan ,cos )P αα在第三象限,则角α的终边位置在( )A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】由于点(tan ,cos )P αα在第三象限,所以tan 0,cos 0αα<<, 所以α在第二象限.故选:B14.(2020·全国高三专题练习(文))已知点(tan ,cos )P αα在第三象限,则角α在第几象限( ) A .第一象限B .第二象限C .第三象限D .第四象限 【答案】B【解析】因为点(tan ,cos )P αα在第三象限,所以tan 0,cos 0αα<< 所以角α在第二象限故选:B15.(2020·江苏高三专题练习)若sin tan 0αα<,且cos 0tan αα<,则角α是第( )象限角. A .一B .二C .三D .四 【答案】C【解析】由条件知sin α与tan α异号,则α为第二或第三象限角;又cos α与tan α异号,则α为第三或第四象限角.综上可知,α为第三象限角.故选:C16.(2020·北京市第十三中学高三期中)已知()0,απ∈,且3cos 5α=-,则tan α=( ) A .43-B .34-C .34D .43 【答案】A【解析】由3cos 5α=-得4sin 5α===±,因为()0,απ∈,所以sin 0α>,所以4sin 5α, 所以4sin 45tan 3cos 35ααα===--,故选:A17.(2020·陕西省定边中学高三月考(文))已知tan 4α=,则21cos 28sin sin 2ααα++的值为( )A ..654C .4D .3【答案】B【解析】因为tan 4α=,所以21cos 28sin sin 2ααα++,222cos 8sin 2sin cos αααα+=,228tan 2tan αα+=,228424+⨯=⨯, 654=故选:B 18.(2020·重庆南开中学高三月考)已知tan 2α=,则2221sin 2cos sin 2cos αααα++=-( )A .32B .52C .4D .5 【答案】D 【解析】22222221sin 2cos sin 2sin cos 2cos sin 2cos sin 2cos αααααααααα++++=--22tan 2tan 25tan 2ααα++==-故选:D 19.(2020·全国高三专题练习(文))已知02πα-<<,1sin cos 5αα+=,则221cos sin αα-的值为( )A .75B .257C .725D .2425【答案】B【解析】由题意,因为1sin cos 5αα+=,所以112sin cos 25αα+=,所以242sin cos 25αα=-, 所以()249cos sin 12sin cos 25αααα-=-=,又因为02πα-<<,所以sin 0,cos 0αα<>,所以7cos sin 5αα-=,所以221125cos sin (cos sin )(cos sin )7αααααα==-+-,故选B.20.(2020·全国高三专题练习)(多选)下列转化结果正确的是( )A .6730'化成弧度是38πB .103π-化成角度是600-C .150-化成弧度是76π-D .12π化成角度是5 【答案】ABD【解析】对于A,3673067.51808ππ'=⨯=,正确;对于B,101018060033πππ-=-⨯=-,正确; 对于C,51501501806ππ⨯-=-=-,错误;对于D,180151212πππ=⨯=,正确.故选ABD 21.(2020·天津经济技术开发区第二中学高三期中)已知角θ的终边经过点(,3)P x (0x <)且cos 10x θ=,则x =___________. 【答案】1-【解析】由余弦函数的定义可得cos 10x θ==,解得0x =(舍去),或1x =(舍去),或1x =-, 1x ∴=-.故答案为:1-.22.(2020·湖南高二学业考试)已知角α的终边经过点(3,4),则cos α=______________.【答案】35【解析】因为角α的终边经过点(3,4),所以3cos 5x r α===,故答案:35 23(2020·天津经济技术开发区第二中学高三期中)已知2sin cos 0αα-=,则2sin 2sin cos ααα-=___________. 【答案】35【解析】由2sin cos 0αα-=,得1tan 2α=,则有222222sin 2sin cos sin 2sin cos tan 2tan 1sin cos tan 1ααααααααααα---==++221123225112⎛⎫-⨯ ⎪⎝⎭==-⎛⎫+ ⎪⎝⎭; 故答案为:35. 24.(2020·万载县第二中学高三月考(理))已知角α的终边经过点(,6)P x --,且3cos 5α=-,则11sin tan αα+=________. 【答案】12- 【解析】点P 的纵坐标为6-,且3cos 05α=-<.∴角α的终边落在第三象限,4sin 5α∴=-,4tan 3α= 115321sin tan 4442αα∴+=-+=-=-.故答案为:12-. 25.(2020·山东高三专题练习)已知sin 2cos 3sin 5cos αααα-+=-5,那么tan α=________. 【答案】-2316易知cos α≠0,由sin 2cos 3sin 5cos αααα-+=-5,得tan 23tan 5αα-+=-5,解得tan α=-2316.故答案为:-2316。

高考一轮复习专题——三角函数第1讲 任意角、弧度制及任意角的三角函数基础梳理1.任意角 (1)角的概念的推广①按旋转方向不同分为正角、负角、零角. ②按终边位置不同分为象限角和轴线角. (2)终边相同的角终边与角α相同的角可写成α+k ·360°(k ∈Z ). (3)弧度制①1弧度的角:把长度等于半径长的弧所对的圆心角叫做1弧度的角. ②规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零, |α|=l r,l 是以角α作为圆心角时所对圆弧的长,r 为半径.③用“弧度”做单位来度量角的制度叫做弧度制,比值lr 与所取的r 的大小无关,仅与角的大小有关.④弧度与角度的换算:360°=2π弧度;180°=π弧度. ⑤弧长公式:l =|α|r ,扇形面积公式:S 扇形=12lr =12|α|r 2.2.任意角的三角函数定义设α是一个任意角,角α的终边上任意一点P (x ,y ),它与原点的距离为r (r >0),那么角α的正弦、余弦、正切分别是:sin α=yr ,cos α=x r,tan α=y x,它们都是以角为自变量,以比值为函数值的函数. 3.三角函数线设角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边与单位圆相交于点P ,过P 作PM 垂直于x 轴于M ,则点M 是点P 在x 轴上的正射影.由三角函数的定义知,点P 的坐标为(cos_α,sin_α),即P (cos_α,sin_α),其中cos α=OM ,sin α=MP ,单位圆与x 轴的正半轴交于点A ,单位圆在A 点的切线与α的终边或其反向延长线相交于点T ,则tan α=AT .我们把有向线段OM 、MP 、AT 叫做α的余弦线、正弦线、正切线.三角函数线有向线段MP 为正弦线有向线段OM 为余弦线有向线段AT为正切线一条规律三角函数值在各象限的符号规律概括为:一全正、二正弦、三正切、四余弦. (2)终边落在x 轴上的角的集合{β|β=kπ,k ∈Z };终边落在y 轴上的角的集合⎭⎬⎫⎩⎨⎧∈+=Z k k ,2ππββ;终边落在坐标轴上的角的集合可以表示为⎭⎬⎫⎩⎨⎧∈=Z k k ,2πββ. 两个技巧(1)在利用三角函数定义时,点P 可取终边上任一点,如有可能则取终边与单位圆的交点,|OP |=r 一定是正值.(2)在解简单的三角不等式时,利用单位圆及三角函数线是一个小技巧. 三个注意(1)注意易混概念的区别:第一象限角、锐角、小于90°的角是概念不同的三类角,第一类是象限角,第二类、第三类是区间角.(2)角度制与弧度制可利用180°=π rad 进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.(3)注意熟记0°~360°间特殊角的弧度表示,以方便解题.双基自测1.(人教A版教材习题改编)下列与9π4的终边相同的角的表达式是( ).A.2kπ+45°(k∈Z) B.k·360°+94π(k∈Z)C.k·360°-315°(k∈Z) D.kπ+5π4(k∈Z)2.若α=k·180°+45°(k∈Z),则α在( ).A.第一或第三象限B.第一或第二象限C.第二或第四象限D.第三或第四象限3.若sin α<0且tan α>0,则α是( ).A.第一象限角B.第二象限角C.第三象限角D.第四象限角4.已知角α的终边过点(-1,2),则cos α的值为( ).A.-55B.255C.-255D.-125.(2011·江西)已知角θ的顶点为坐标原点,始边为x轴非负半轴,若P(4,y)是角θ终边上一点,且sin θ=-255,则y=________.考向一角的集合表示及象限角的判定【例1】►(1)写出终边在直线y=3x上的角的集合;(2)若角θ的终边与6π7角的终边相同,求在[0,2π)内终边与θ3角的终边相同的角;(3)已知角α是第二象限角,试确定2α、α2所在的象限.【训练1】角α与角β的终边互为反向延长线,则( ).A.α=-βB.α=180°+βC.α=k·360°+β(k∈Z)D .α=k ·360°±180°+β(k ∈Z )考向二 三角函数的定义【例2】►已知角θ的终边经过点P (-3,m )(m ≠0)且sin θ=24m ,试判断角θ所在的象限,并求cos θ和tan θ的值.【训练2】(2011·课标全国)已知角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边在直线y =2x 上,则cos 2θ=( ). A .-45 B .-35 C.35 D.45考向三 弧度制的应用【例3】►已知半径为10的圆O 中,弦AB 的长为10. (1)求弦AB 所对的圆心角α的大小;(2)求α所在的扇形的弧长l 及弧所在的弓形的面积S .【训练3】已知扇形周长为40,当它的半径和圆心角取何值时,才使扇形面积最大?考向四 三角函数线及其应用【例4】►在单位圆中画出适合下列条件的角α的终边的范围.并由此写出角α的集合: (1)sin α≥32; (2)cos α≤-12.【训练4】求下列函数的定义域:(1)y =2cos x -1; (2)y =lg(3-4sin 2x ). 解 (1)∵2cos x -1≥0,∴cos x ≥12.重点突破——如何利用三角函数的定义求三角函数值【问题研究】三角函数的定义:设α是任意角,其终边上任一点P (不与原点重合)的坐标为(x ,y ),它到原点的距离是r (r =x 2+y 2>0),则sin α=yr、cosα=x r 、tan α=yx 分别是α的正弦、余弦、正切,它们都是以角为自变量,以比值为函数值的函数,这样的函数称为三角函数,这里x ,y 的符号由α终边所在象限确定,r 的符号始终为正,应用定义法解题时,要注意符号,防止出现错误.三角函数的定义在解决问题中应用广泛,并且有时可以简化解题过程.【解决方案】利用三角函数的定义求三角函数值时,首先要根据定义正确地求得x ,y ,r 的值;然后对于含参数问题要注意分类讨论.【示例】►(本题满分12分)(2011·龙岩月考)已知角α终边经过点P (x ,-2)(x ≠0),且cos α=36x ,求sin α、tan α的值.【试一试】已知角α的终边在直线3x +4y =0上,求sin α+cos α+45tan α.第2讲 同角三角函数的基本关系与诱导公式基础梳理1.同角三角函数的基本关系 (1)平方关系:sin 2α+cos 2α=1; (2)商数关系:sin αcos α=tan α.2.诱导公式公式一:sin(α+2k π)=sin α,cos(α+2k π)=cos α,其中k ∈Z .公式二:sin(π+α)=-sin α,cos(π+α)=-cos α, tan(π+α)=tan α.公式三:sin(-α)=-sin α,cos(-α)=cos α. 公式四:sin(π-α)=sin α,cos(π-α)=-cos α. 公式五:sin )2(απ-=cos α,cos )2(απ-=sin α.公式六:sin )2(απ+=cos α,cos )2(απ+=-sin α. 诱导公式可概括为k ·π2±α的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.其中的奇、偶是指π2的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称变为相应的余名函数;若是偶数倍,则函数名称不变,符号看象限是指把α看成锐角时原函数值的符号作为结果的符号.一个口诀诱导公式的记忆口诀为:奇变偶不变,符号看象限.三种方法在求值与化简时,常用方法有: (1)弦切互化法:主要利用公式tan α=sin αcos α化成正、余弦.(2)和积转换法:利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化.(3)巧用“1”的变换:1=sin 2θ+cos 2θ=cos 2θ(1+tan 2θ)=tan π4=…. 三个防范(1)利用诱导公式进行化简求值时,先利用公式化任意角的三角函数为锐角三角函数,其步骤:去负-脱周-化锐. 特别注意函数名称和符号的确定.(2)在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. (3)注意求值与化简后的结果一般要尽可能有理化、整式化.双基自测1.(人教A 版教材习题改编)已知sin(π+α)=12,则cos α的值为( ).A .±12 B.12 C.32 D .±322.(2012·杭州调研)点A (sin 2 011°,cos 2 011°)在直角坐标平面上位于( ). A .第一象限 B .第二象限 C .第三象限D .第四象限3.已知cos α=45,α∈(0,π),则tan α的值等于( ).A.43B.34 C .±43 D .±344.cos )417(π--sin )417(π-的值是( ). A. 2 B .- 2 C .0 D.225.已知α是第二象限角,tan α=-12,则cos α=________.考向一 利用诱导公式化简、求值【例1】►已知)tan()2sin()2cos()sin()(απαπαπαπα++--=f ,求【训练1】已知角α终边上一点P (-4,3),则的值为________.考向二 同角三角函数关系的应用)3(πf )29sin()211cos()sin()2cos(απαπαπαπ+---+【例2】►(2011·长沙调研)已知tan α=2. 求:(1)2sin α-3cos α4sin α-9cos α;(2)4sin 2α-3sin αcos α-5cos 2α.【训练2】已知sin α+3cos α3cos α-sin α=5.则sin 2α-sin αcos α=________.考向三 三角形中的诱导公式【例3】►在△ABC 中,sin A +cos A =2,3cos A =-2cos(π-B ),求△ABC 的三个内角.【训练3】若将例3的已知条件“sin A +cos A =2”改为“sin(2π-A )=-2sin(π-B )”其余条件不变,求△ABC 的三个内角.重点突破——忽视题设的隐含条件致误【问题诊断】涉及到角的终边、函数符号和同角函数关系问题时,应深挖隐含条件,处理好开方、平方关系,避免出现增解与漏解的错误.,【防范措施】一要考虑题设中的角的范围;二要考虑题设中的隐含条件 【示例】►若sin θ,cos θ是关于x 的方程5x 2-x +a =0(a 是常数)的两根,θ∈(0,π),求cos 2θ的值.【试一试】已知sin θ+cos θ=713,θ∈(0,π),求tan θ.第3讲 三角函数的图象与性质基础梳理1.“五点法”描图(1)y =sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0),)1,2(π,(π,0),)1,23(-π,(2π,0).(2)y =cos x 的图象在[0,2π]上的五个关键点的坐标为(0,1),)0,2(π,(π,-1),)0,23(π,(2π,1).2.三角函数的图象和性质定义域R R {x|x≠kπ+π2,k∈Z}图象值域[-1,1][-1,1]R对称性对称轴:x=kπ+π2(k∈Z)对称中心:(kπ,0)(k∈Z)对称轴:x=kπ(k∈Z)对称中心:错误!无对称轴对称中心:)0,2(πk(k∈Z)周期2π2ππ单调性单调增区间⎥⎦⎤⎢⎣⎡+-22,22ππππkk(k∈Z);单调减区间⎥⎦⎤⎢⎣⎡++ππππ232,22kk(k∈Z)单调增区间[2kπ-π,2kπ](k∈Z);单调减区间[2kπ,2kπ+π](k∈Z)单调增区间)2,2(ππππ+-kk(k∈Z)奇偶性奇偶奇两条性质(1)周期性函数y=A sin(ωx+φ)和y=A cos(ωx+φ)的最小正周期为2π|ω|,y=tan(ωx+φ)的最小正周期为π|ω|.(2)奇偶性三角函数中奇函数一般可化为y =A sin ωx 或y =A tan ωx ,而偶函数一般可化为y =A cos ωx +b 的形式.三种方法求三角函数值域(最值)的方法: (1)利用sin x 、cos x 的有界性;(2)形式复杂的函数应化为y =A sin(ωx +φ)+k 的形式逐步分析ωx +φ的范围,根据正弦函数单调性写出函数的值域;(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题.双基自测1.(人教A 版教材习题改编)函数y =cos )3(π+x ,x ∈R ( ).A .是奇函数B .是偶函数C .既不是奇函数也不是偶函数D .既是奇函数又是偶函数2.函数y =tan )4(x -π的定义域为( ).A.⎭⎬⎫⎩⎨⎧∈-≠Z k k x x ,4ππB.⎭⎬⎫⎩⎨⎧∈-≠Z k k x x ,42ππC.⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,4ππD.⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,42ππ3.(2011·全国新课标)设函数f (x )=sin(ωx +φ)+cos(ωx +φ)(20πϕω<,>)的最小正周期为π,且f (-x )=f (x ),则( ). A .f (x )在)2,0(π单调递减B .f (x )在)43,4(ππ单调递减C .f (x )在)2,0(π单调递增D .f (x )在)43,4(ππ单调递增4.y =sin )4(π-x 的图象的一个对称中心是( ).A .(-π,0) B.)0,43(π-C.)0,23(π D.)0,2(π5.(2011·合肥三模)函数f (x )=cos )62(π+x 的最小正周期为________.考向一 三角函数的定义域与值域【例1】►(1)求函数y =lg sin 2x +9-x 2的定义域. (2)求函数y =cos 2x +sin x (4π≤x )的最大值与最小值.【训练1】(1)求函数y =sin x -cos x 的定义域.(2)已知函数f (x )=cos )32(π-x +2sin )4(π-x ·sin )4(π+x ,求函数f (x )在区间⎥⎦⎤⎢⎣⎡-2,12ππ上的最大值与最小值.考向二 三角函数的奇偶性与周期性【例2】►(2011·大同模拟)函数y =2cos 2)4(π-x -1是( ).A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为π2的奇函数D .最小正周期为π2的偶函数 【训练2】已知函数f (x )=(sin x -cos x )sin x ,x ∈R ,则f (x )的最小正周期是________.考向三 三角函数的单调性【例3】►已知f (x )=sin x +sin )2(x -π,x ∈[0,π],求f (x )的单调递增区间.【训练3】函数f (x )=sin )32(π+-x 的单调减区间为______.考向四 三角函数的对称性【例4】►(1)函数y =cos )32(π+x 图象的对称轴方程可能是( ).A .x =-π6B .x =-π12C .x =π6D .x =π12【训练4】(1)函数y =2sin(3x +φ)(2πϕ<)的一条对称轴为x =π12,则φ=________.(2)函数y =cos(3x +φ)的图象关于原点成中心对称图形.则φ=________.重点突破——利用三角函数的性质求解参数问题含有参数的三角函数问题,一般属于逆向型思维问题,难度相对较大一些.正确利用三角函数的性质解答此类问题,是以熟练掌握三角函数的各条性质为前提的,解答时通常将方程的思想与待定系数法相结合.下面就利用三角函数性质求解参数问题进行策略性的分类解析. 一、根据三角函数的单调性求解参数【示例】►(2011·镇江三校模拟)已知函数f (x )=sin )3(πω+x (ω>0)的单调递增区间为⎥⎦⎤⎢⎣⎡+-12,125ππππk k (k ∈Z ),单调递减区间为⎥⎦⎤⎢⎣⎡++127,12ππππk k (k ∈Z ),则ω的值为________.二、根据三角函数的奇偶性求解参数【示例】► (2011·泉州模拟)已知f (x )=cos(3x +φ)-3sin(3x +φ)为偶函数,则φ可以取的一个值为( ). A.π6 B.π3 C .-π6 D .-π3▲根据三角函数的周期性求解参数【示例】► (2011·合肥模拟)若函数y =sin ωx ·sin )2(πω+x (ω>0)的最小正周期为π7,则ω=________.▲根据三角函数的最值求参数【示例】► (2011·洛阳模拟)若函数f(x)=a sin x-b cos x在x=π3处有最小值-2,则常数a、b的值是( ).A.a=-1,b= 3 B.a=1,b=- 3C.a=3,b=-1 D.a=-3,b=1第4讲正弦型函数y=A sin(ωx+φ)的图象及应用基础梳理1.用五点法画y=A sin(ωx+φ)一个周期内的简图时,要找五个特征点如下表所示x 0-φωπ2-φωπ-φω3π2-φω2π-φωωx+φ0π2π3π22πy=A sin(ωx+φ)0 A 0-A 0 2.函数y=sin x的图象变换得到y=A sin(ωx+φ)的图象的步骤3.图象的对称性函数y =A sin(ωx +φ)(A >0,ω>0)的图象是轴对称也是中心对称图形,具体如下:(1)函数y =A sin(ωx +φ)的图象关于直线x =x k (其中 ωx k +φ=k π+π2,k∈Z )成轴对称图形.(2)函数y =A sin(ωx +φ)的图象关于点(x k,0)(其中ωx k +φ=k π,k ∈Z )成中心对称图形. 一种方法在由图象求三角函数解析式时,若最大值为M ,最小值为m ,则A =M -m 2,k =M +m 2,ω由周期T 确定,即由2πω=T 求出,φ由特殊点确定.一个区别由y =sin x 的图象变换到y =A sin (ωx +φ)的图象,两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是|φ|个单位;而先周期变换(伸缩变换)再相位变换,平移的量是|φ|ω(ω>0)个单位.原因在于相位变换和周期变换都是针对x 而言,即x 本身加减多少值,而不是依赖于ωx 加减多少值. 两个注意作正弦型函数y =A sin(ωx +φ)的图象时应注意: (1)首先要确定函数的定义域;(2)对于具有周期性的函数,应先求出周期,作图象时只要作出一个周期的图象,就可根据周期性作出整个函数的图象.双基自测1.(人教A 版教材习题改编)y =2sin )42(π-x 的振幅、频率和初相分别为( ). A .2,1π,-π4 B .2,12π,-π4 C .2,1π,-π8D .2,12π,-π82.已知简谐运动f (x )=A sin(ωx +φ)(2πϕ<)的部分图象如图所示,则该简谐运动的最小正周期T 和初相φ分别为( ). A .T =6π,φ=π6B .T =6π,φ=π3C .T =6,φ=π6D .T =6,φ=π33.函数y =cos x (x ∈R )的图象向左平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式应为( ).A .-sin xB .sin xC .-cos xD .cos x4.设ω>0,函数y =sin )3(πω+x +2的图象向右平移4π3个单位后与原图象重合,则ω的最小值是( ). A.23 B.43 C.32D .35.(2011·重庆六校联考)已知函数f (x )=sin(ωx +φ)(ω>0)的图象如图所示,则ω=________.考向一 作函数y =A sin(ωx +φ)的图象【例1】►设函数f (x )=cos(ωx +φ)(02-0<<,>ϕπω)的最小正周期为π,且)4(πf =32.(1)求ω和φ的值;(2)在给定坐标系中作出函数f (x )在[0,π]上的图象.【训练1】已知函数f (x )=3sin )421(π-x ,x ∈R .(1)画出函数f (x )在长度为一个周期的闭区间上的简图; (2)将函数y =sin x 的图象作怎样的变换可得到f (x )的图象?考向二 求函数y =A sin(ωx +φ)的解析式【例2】►(2011·江苏)函数f (x )=A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)的部分图象如图所示,则f (0)的值是________.【训练2】已知函数y =A sin(ωx +φ)(A >0,|φ|<π2,ω>0)的图象的一部分如图所示. (1)求f (x )的表达式; (2)试写出f (x )的对称轴方程.考向三 函数y =A sin(ωx +φ)的图象与性质的综合应用【例3】►(2012·西安模拟)已知函数f (x )=A sin(ωx +φ),x ∈R (其中A >0,ω>0,0<φ<π2)的图象与x 轴的交点中,相邻两个交点之间的距离为π2,且图象上的一个最低点为M )2,32(-π. (1)求f (x )的解析式;(2)当x ∈⎥⎦⎤⎢⎣⎡2,12ππ时,求f (x )的值域.【训练3】(2011·南京模拟)已知函数y =A sin(ωx +φ)(A >0,ω>0)的图象过点P )0,12(π,图象上与点P 最近的一个最高点是Q )5,3(π.(1)求函数的解析式; (2)求函数f (x )的递增区间.重点突破——怎样求解三角函数的最值问题【问题研究】(1)求三角函数的最值是高考的一个热点.在求解中,一定要注意其定义域,否则容易产生错误.(2)主要题型:①求已知三角函数的值域(或最值);②根据三角函数的值域(或最值)求相关的参数;③三角函数的值域(或最值)作为工具解决其他与范围相关的问题.【解决方案】①形如y =a sin x +b cos x +c 的三角函数,可通过引入辅助角Φ(2222sin ,cos b a b b a a +=+=φφ),将原式化为y =a 2+b 2·sin(x +φ)+c的形式后,再求值域(或最值);②形如y =a sin 2x +b sin x +c 的三角函数,可先设t =sin x ,将原式化为二次函数y =at 2+bt +c 的形式,进而在t ∈[-1,1]上求值域(或最值);③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,将原式化为二次函数y =±12a (t 2-1)+bt +c 的形式,进而在闭区间t ∈[-2,2]上求最值.【示例】►(本题满分12分)(2011·北京)已知函数f (x )=4cos x sin )6(π+x -1.(1)求f (x )的最小正周期;(2)求f (x )在区间⎥⎦⎤⎢⎣⎡-4,6ππ上的最大值和最小值.【试一试】是否存在实数a ,使得函数y =sin 2x +a cos x +58a -32在闭区间⎥⎦⎤⎢⎣⎡2,0π上的最大值是1?若存在,求出对应的a 值?若不存在,试说明理由.第5讲 两角和与差的正弦、余弦和正切基础梳理1.两角和与差的正弦、余弦、正切公式(1)C (α-β):cos(α-β)=cos αcos β+sin αsin β; (2)C (α+β):cos(α+β)=cos αcos β-sin αsin β; (3)S (α+β):sin(α+β)=sin αcos β+cos_αsin β; (4)S (α-β):sin(α-β)=sin αcos β-cos αsin β; (5)T (α+β):tan(α+β)=tan α+tan β1-tan αtan β;(6)T (α-β):tan(α-β)=tan α-tan β1+tan αtan β.2.二倍角的正弦、余弦、正切公式 (1)S 2α:sin 2α=2sin_αcos_α;(2)C 2α:cos 2α=cos 2α-sin 2α=2cos 2α-1=1-2sin 2α; (3)T 2α:tan 2α=2tan α1-tan 2α.3.有关公式的逆用、变形等(1)tan α±tan β=tan(α±β)(1∓tan_αtan_β); (2)cos 2α=1+cos 2α2,sin 2α=1-cos 2α2; (3)1+sin 2α=(sin α+cos α)2,1-sin 2α=(sin α-cos α)2, sin α±cos α=2sin )4(πα±.4.函数f (α)=a cos α+b sin α(a ,b 为常数),可以化为f (α)=a 2+b 2sin(α+φ)或f (α)=a 2+b 2cos(α-φ),其中φ可由a ,b 的值唯一确定.两个技巧(1)拆角、拼角技巧:2α=(α+β)+(α-β);α=(α+β)-β;β=α+β2-α-β2;α-β2=)2(βα+-)2(βα+.(2)化简技巧:切化弦、“1”的代换等.三个变化(1)变角:目的是沟通题设条件与结论中所涉及的角,其手法通常是“配凑”. (2)变名:通过变换函数名称达到减少函数种类的目的,其手法通常有“切化弦”、“升幂与降幂”等.(3)变式:根据式子的结构特征进行变形,使其更贴近某个公式或某个期待的目标,其手法通常有:“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.双基自测1.(人教A 版教材习题改编)下列各式的值为14的是( ).A .2cos 2 π12-1 B .1-2sin 275° C.2tan 22.5°1-tan 222.5°D .sin 15°cos 15° 2.(2011·福建)若tan α=3,则sin 2αcos 2α的值等于( ).A .2B .3C .4D .6 3.已知sin α=23,则cos(π-2α)等于( ).A .-53 B .-19 C.19 D.534.(2011·辽宁)设sin )4(θπ+=13,则sin 2θ=( ).A .-79B .-19 C.19 D.795.tan 20°+tan 40°+3tan 20° tan 40°=________.考向一 三角函数式的化简【例1】►化简)4(sin )4tan(221cos 2cos 2224x x x x +-+-ππ.【训练1】化简:ααααα2sin )1cos )(sin 1cos (sin +--+.考向二 三角函数式的求值【例2】►已知0<β<π2<α<π,且cos )2(βα-=-19,sin )2(βα-=23,求cos(α+β)的值.【训练2】已知α,β∈)2,0(π,sin α=45,tan(α-β)=-13,求cos β的值.考向三 三角函数的求角问题【例3】►已知cos α=17,cos(α-β)=1314,且0<β<α<π2,求β.【训练3】已知α,β∈)2,2(ππ-,且tan α,tan β是方程x 2+33x +4=0的两个根,求α+β的值.考向四 三角函数的综合应用【例4】►(2010·北京)已知函数f (x )=2cos 2x +sin 2x .(1)求f )3(π的值;(2)求f (x )的最大值和最小值.【训练4】已知函数f (x )=2sin(π-x )cos x . (1)求f (x )的最小正周期;(2)求f (x )在区间⎥⎦⎤⎢⎣⎡-2,6ππ上的最大值和最小值.重点突破——三角函数求值、求角问题策略面对有关三角函数的求值、化简和证明,许多考生一筹莫展,而三角恒等变换更是三角函数的求值、求角问题中的难点和重点,其难点在于:其一,如何牢固记忆众多公式,其二,如何根据三角函数的形式去选择合适的求值、求角方法. 一、给值求值一般是给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如α=(α+β)-β,2α=(α+β)+(α-β)等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论.【示例】► (2011·江苏)已知tan )4(π+x =2,则tan x tan 2x 的值为________.二、给值求角“给值求角”:实质上也转化为“给值求值”,关键也是变角,把所求角用含已知角的式子表示,由所得的函数值结合该函数的单调区间求得角.【示例】► (2011·南昌月考)已知tan(α-β)=12,tan β=-17,且α,β∈(0,π),求2α-β的值.▲三角恒等变换与向量的综合问题两角和与差的正弦、余弦、正切公式作为解题工具,是每年高考的必考内容,常在选择题中以条件求值的形式考查.近几年该部分内容与向量的综合问题常出现在解答题中,并且成为高考的一个新考查方向.【示例】► (2011·温州一模)已知向量a =(sin θ,-2)与b =(1,cos θ)互相垂直,其中θ∈)2,0(π.(1)求sin θ和cos θ的值;(2)若5cos(θ-φ)=35cos φ,0<φ<π2,求cos φ的值.第6讲正弦定理和余弦定理基础梳理1.正弦定理:asin A =bsin B=csin C=2R,其中R是三角形外接圆的半径.由正弦定理可以变形为:(1)a∶b∶c=sin A∶sin B∶sin C;(2)a=2R sin_A,b=2R sin_B,c=2R sin_C;(3)sin A=a2R,sin B=b2R,sin C=c2R等形式,以解决不同的三角形问题.2.余弦定理:a2=b2+c2-2bc cos A,b2=a2+c2-2ac cos B,c2=a2+b2-2ab cos C.余弦定理可以变形为:cos A=b2+c2-a22bc,cos B=a2+c2-b22ac,cos C=a2+b2-c22ab.3.S△ABC=12ab sin C=12bc sin A=12ac sin B=abc4R=12(a+b+c)·r(R是三角形外接圆半径,r是三角形内切圆的半径),并可由此计算R,r.4.已知两边和其中一边的对角,解三角形时,注意解的情况.如已知a,b,A,则A为锐角A为钝角或直角图形关系式a<b sin A a=b sin Ab sin A<a<ba≥b a>b a≤b解的个数无解一解两解一解一解无解一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ABC中,A>B⇔a>b⇔sin A>sin B.两类问题在解三角形时,正弦定理可解决两类问题:(1)已知两角及任一边,求其它边或角;(2)已知两边及一边的对角,求其它边或角.情况(2)中结果可能有一解、两解、无解,应注意区分.余弦定理可解决两类问题:(1)已知两边及夹角求第三边和其他两角;(2)已知三边,求各角.两种途径根据所给条件确定三角形的形状,主要有两种途径:(1)化边为角;(2)化角为边,并常用正弦(余弦)定理实施边、角转换.双基自测1.(人教A版教材习题改编)在△ABC中,A=60°,B=75°,a=10,则c等于( ).A.5 2 B.10 2C.1063D.5 62.在△ABC中,若sin Aa=cos Bb,则B的值为( ).A.30° B.45° C.60° D.90°3.(2011·郑州联考)在△ABC中,a=3,b=1,c=2,则A等于( ). A.30° B.45° C.60° D.75°4.在△ABC中,a=32,b=23,cos C=13,则△ABC的面积为( ).A.3 3 B.2 3 C.4 3 D. 35.已知△ABC三边满足a2+b2=c2-3ab,则此三角形的最大内角为________.考向一利用正弦定理解三角形【例1】►在△ABC中,a=3,b=2,B=45°.求角A,C和边c.【训练1】(2011·北京)在△ABC中,若b=5,∠B=π4,tan A=2,则sin A=________;a=________.考向二利用余弦定理解三角形【例2】►在△ABC中,a、b、c分别是角A、B、C的对边,且cos Bcos C=-b2a+c.(1)求角B的大小;(2)若b=13,a+c=4,求△ABC的面积.【训练2】(2011·桂林模拟)已知A,B,C为△ABC的三个内角,其所对的边分别为a,b,c,且2cos2A2+cos A=0.(1)求角A的值;(2)若a=23,b+c=4,求△ABC的面积.考向三 利用正、余弦定理判断三角形形状【例3】►在△ABC 中,若(a 2+b 2)sin(A -B )=(a 2-b 2)sin C ,试判断△ABC 的形状.【训练3】在△ABC 中,若a cos A =b cos B =c cos C ;则△ABC 是( ). A .直角三角形B .等边三角形C .钝角三角形D .等腰直角三角形考向四 正、余弦定理的综合应用【例3】►在△ABC 中,内角A ,B ,C 对边的边长分别是a ,b ,c ,已知c =2,C =π3. (1)若△ABC 的面积等于3,求a ,b ;(2)若sin C +sin(B -A )=2sin 2A ,求△ABC 的面积.【训练4】(2011·北京西城一模)设△ABC 的内角A ,B ,C 所对的边长分别为a ,b,c,且cos B=45,b=2.(1)当A=30°时,求a的值;(2)当△ABC的面积为3时,求a+c的值.重点突破——忽视三角形中的边角条件致错【问题诊断】考查解三角形的题在高考中一般难度不大,但稍不注意,会出现“会而不对,对而不全”的情况,其主要原因就是忽视三角形中的边角条件., 【防范措施】解三角函数的求值问题时,估算是一个重要步骤,估算时应考虑三角形中的边角条件.【示例】►(2011·安徽)在△ABC中,a,b,c分别为内角A,B,C所对的边长,a=3,b=2,1+2cos(B+C)=0,求边BC上的高.【试一试】(2011·辽宁)△ABC的三个内角A,B,C所对的边分别为a,b,c,a sin A sin B+b cos2A=2a.(1)求b a ;(2)若c2=b2+3a2,求B.第7讲正弦定理、余弦定理应用举例基础梳理1.用正弦定理和余弦定理解三角形的常见题型测量距离问题、高度问题、角度问题、计算面积问题、航海问题、物理问题等.2.实际问题中的常用角(1)仰角和俯角在视线和水平线所成的角中,视线在水平线上方的角叫仰角,在水平线下方的角叫俯角(如图(1)).(2)方位角指从正北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图(2)).(3)方向角:相对于某正方向的水平角,如南偏东30°,北偏西45°,西偏东60°等.(4)坡度:坡面与水平面所成的二面角的度数.一个步骤解三角形应用题的一般步骤:(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.(3)根据题意选择正弦定理或余弦定理求解.(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.两种情形解三角形应用题常有以下两种情形(1)实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理求解.(2)实际问题经抽象概括后,已知量与未知量涉及到两个或两个以上的三角形,这时需作出这些三角形,先解够条件的三角形,然后逐步求解其他三角形,有时需设出未知量,从几个三角形中列出方程(组),解方程(组)得出所要求的解.双基自测1.(人教A版教材习题改编)如图,设A,B两点在河的两岸,一测量者在A所在的同侧河岸边选定一点C,测出AC的距离为50 m,∠ACB=45°,∠CAB=105°后,就可以计算出A,B两点的距离为( ).A.50 2 m B.50 3 m C.25 2 m D.2522m2.从A处望B处的仰角为α,从B处望A处的俯角为β,则α,β的关系为( ). A.α>β B.α=βC.α+β=90° D.α+β=180°3.若点A在点C的北偏东30°,点B在点C的南偏东60°,且AC=BC,则点A 在点B的( ).A.北偏东15° B.北偏西15°C.北偏东10°D.北偏西10°4.一船向正北航行,看见正西方向相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时( ).A.5海里B.53海里C.10海里D.103海里5.海上有A,B,C三个小岛,测得A,B两岛相距10海里,∠BAC=60°,∠ABC =75°,则B,C间的距离是________海里.考向一测量距离问题【例1】►如图所示,为了测量河对岸A,B两点间的距离,在这岸定一基线CD,现已测出CD=a和∠ACD=60°,∠BCD=30°,∠BDC=105°,∠ADC=60°,试求AB的长.【训练1】如图,A,B,C,D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°,30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B,D的距离.考向二测量高度问题【例2】►如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.【训练2】如图所示,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=α,∠BDC=β,CD=s,并在点C测得塔顶A的仰角为θ,求塔高AB.考向三正、余弦定理在平面几何中的综合应用【例3】►如图所示,在梯形ABCD中,AD∥BC,AB=5,AC=9,∠BCA=30°,∠ADB=45°,求BD的长.【训练3】如图,在△ABC中,已知∠B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.重点突破——如何运用解三角形知识解决实际问【问题研究】1.解三角形实际应用问题的一般步骤是:审题——建模准确地画出图形——求解——检验作答;2.三角形应用题常见的类型:①实际问题经抽象概括后,已知量与未知量全部集中在一个三角形中,可用正弦定理或余弦定理解之;②实际问题经抽象概括后,已知量与未知量涉及两个三角形,这时需按顺序逐步在两个三角形中求出问题的解;③实际问题经抽象概括后,涉及的三角形只有一个,但由题目已知条件解此三角形需连续使用正弦定理或余弦定理.【解决方案】航海、测量问题利用的就是目标在不同时刻的位置数据,这些数据反映在坐标系中就构成了一些三角形,根据这些三角形就可以确定目标在一定的时间内的运动距离,因此解题的关键就是通过这些三角形中的已知数据把测量目标归入到一个可解三角形中.【示例】►(本题满分12分)如图,甲船以每小时302海里的速度向正北方航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里,当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距102海里.问:乙船每小时航行多少海里?【试一试】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°、相距20海里的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,求cos θ.。
2024年高考数学总复习第四章《三角函数、解三角形》§4.1任意角、弧度制及任意角的三角函数最新考纲1.了解任意角的概念和弧度制,能进行弧度与角度的互化.2.借助单位圆理解任意角三角函数(正弦、余弦、正切)的定义.1.角的概念(1)任意角:①定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形;②分类:角按旋转方向分为正角、负角和零角.(2)所有与角α终边相同的角,连同角α在内,构成的角的集合是S ={β|β=k ·360°+α,k ∈Z }.(3)象限角:使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,那么,角的终边在第几象限,就说这个角是第几象限角;如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.2.弧度制(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,用符号rad 表示,读作弧度.正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0.(2)角度制和弧度制的互化:180°=πrad,1°=π180rad ,1rad(3)扇形的弧长公式:l =|α|·r ,扇形的面积公式:S =12lr =12|α|·r 2.3.任意角的三角函数任意角α的终边与单位圆交于点P (x ,y )时,则sin α=y ,cos α=x ,tan α=yx (x ≠0).三个三角函数的性质如下表:三角函数定义域第一象限符号第二象限符号第三象限符号第四象限符号sin αR++--cos αR+--+tan α{α|α≠k π+π2,k ∈Z }+-+-4.三角函数线如下图,设角α的终边与单位圆交于点P ,过P 作PM ⊥x 轴,垂足为M ,过A (1,0)作单位圆的切线与α的终边或终边的反向延长线相交于点T .三角函数线有向线段MP 为正弦线;有向线段OM 为余弦线;有向线段AT 为正切线概念方法微思考1.总结一下三角函数值在各象限的符号规律.提示一全正、二正弦、三正切、四余弦.2.三角函数坐标法定义中,若取点P (x ,y )是角α终边上异于顶点的任一点,怎样定义角α的三角函数?提示设点P 到原点O 的距离为r ,则sin α=y r ,cos α=x r ,tan α=yx(x ≠0).题组一思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)锐角是第一象限的角,第一象限的角也都是锐角.(×)(2)角α的三角函数值与其终边上点P 的位置无关.(√)(3)不相等的角终边一定不相同.(×)(4)若α为第一象限角,则sin α+cos α>1.(√)题组二教材改编2.角-225°=弧度,这个角在第象限.答案-5π4二3.若角α的终边经过点-22,sin α=,cos α=.答案22-224.一条弦的长等于半径,这条弦所对的圆心角大小为弧度.答案π3题组三易错自纠5|k π+π4≤α≤k π+π2,k ∈Z(阴影部分)是()答案C解析当k =2n (n ∈Z )时,2n π+π4≤α≤2n π+π2,此时α表示的范围与π4≤α≤π2表示的范围一样;当k =2n +1(n ∈Z )时,2n π+π+π4≤α≤2n π+π+π2,此时α表示的范围与π+π4≤α≤π+π2表示的范围一样,故选C.6.已知点Pθ的终边上,且θ∈[0,2π),则θ的值为()A.5π6B.2π3C.11π6D.5π3答案C解析因为点P所以根据三角函数的定义可知tan θ=-1232=-33,又θθ=11π6.7.在0到2π范围内,与角-4π3终边相同的角是.答案2π3解析与角-4π3终边相同的角是2k πk ∈Z ),令k =1,可得与角-4π3终边相同的角是2π3.8.(2018·济宁模拟)函数y =2cos x -1的定义域为.答案2k π-π3,2k π+π3(k ∈Z )解析∵2cos x -1≥0,∴cos x ≥12.由三角函数线画出x 满足条件的终边范围(如图阴影部分所示),∴x ∈2k π-π3,2k π+π3(k ∈Z ).题型一角及其表示1.下列与角9π4的终边相同的角的表达式中正确的是()A .2k π+45°(k ∈Z )B .k ·360°+9π4(k ∈Z )C .k ·360°-315°(k ∈Z )D .k π+5π4(k ∈Z )答案C解析与角9π4的终边相同的角可以写成2k π+9π4(k ∈Z ),但是角度制与弧度制不能混用,所以只有答案C 正确.2.设集合M |x =k2·180°+45°,k ∈ZN |x =k4·180°+45°,k ∈Z()A .M =NB .M ⊆NC .N ⊆MD .M ∩N =∅答案B解析由于M 中,x =k2·180°+45°=k ·90°+45°=(2k +1)·45°,2k +1是奇数;而N 中,x =k4·180°+45°=k ·45°+45°=(k +1)·45°,k +1是整数,因此必有M ⊆N ,故选B.3.(2018·宁夏质检)终边在直线y =3x 上,且在[-2π,2π)内的角α的集合为.答案-53π,-23π,π3,43π解析如图,在坐标系中画出直线y =3x ,可以发现它与x 轴的夹角是π3,在[0,2π)内,终边在直线y =3x 上的角有两个:π3,43π;在[-2π,0)内满足条件的角有两个:-23π,-53π,故满足条件的角α构成的集合为-53,-23π,π3,43π4.若角α是第二象限角,则α2是第象限角.答案一或三解析∵α是第二象限角,∴π2+2k π<α<π+2k π,k ∈Z ,∴π4+k π<α2<π2+k π,k ∈Z .当k 为偶数时,α2是第一象限角;当k 为奇数时,α2是第三象限角.综上,α2是第一或第三象限角.思维升华(1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k (k ∈Z )赋值来求得所需的角.(2)确定kα,αkk ∈N *)的终边位置的方法先写出kα或αk 的范围,然后根据k 的可能取值确定kα或αk的终边所在位置.题型二弧度制及其应用例1已知一扇形的圆心角为α,半径为R ,弧长为l .若α=π3,R =10cm ,求扇形的面积.解由已知得α=π3,R =10cm ,∴S 扇形=12α·R 2=12·π3·102=50π3(cm 2).引申探究1.若例题条件不变,求扇形的弧长及该弧所在弓形的面积.解l =α·R =π3×10=10π3(cm),S 弓形=S 扇形-S 三角形=12·l ·R -12·R 2·sin π3=12·10π3·10-12·102·32=50π-7533(cm 2).2.若例题条件改为:“若扇形周长为20cm ”,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?解由已知得,l +2R =20,则l =20-2R (0<R <10).所以S =12lR =12(20-2R )R =10R -R 2=-(R -5)2+25,所以当R =5cm 时,S 取得最大值25cm 2,此时l =10cm ,α=2rad.思维升华应用弧度制解决问题的方法(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须是弧度.(2)求扇形面积最大值的问题时,常转化为二次函数的最值问题.(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角所在的三角形.跟踪训练1(1)(2018·湖北七校联考)若圆弧长度等于圆内接正三角形的边长,则其圆心角的弧度数为()A.π6B.π3C .3D.3答案D解析如图,等边三角形ABC 是半径为r 的圆O 的内接三角形,则线段AB 所对的圆心角∠AOB =2π3,作OM ⊥AB ,垂足为M ,在Rt △AOM 中,AO =r ,∠AOM =π3,∴AM =32r ,AB =3r ,∴l =3r ,由弧长公式得α=l r =3rr= 3.(2)一扇形是从一个圆中剪下的一部分,半径等于圆半径的23,面积等于圆面积的527,则扇形的弧长与圆周长之比为.答案518解析设圆的半径为r ,则扇形的半径为2r3,记扇形的圆心角为α,由扇形面积等于圆面积的527,可得12α2r 3πr 2=527,解得α=5π6.所以扇形的弧长与圆周长之比为l C =5π6·2r 32πr =518.题型三三角函数的概念命题点1三角函数定义的应用例2(1)(2018·青岛模拟)已知角α的终边与单位圆的交点为-12,sin α·tan α等于()A .-33B .±33C .-32D .±32答案C解析由OP 2=14+y 2=1,得y 2=34,y =±32.当y =32时,sin α=32,tan α=-3,此时,sin α·tan α=-32.当y =-32时,sin α=-32,tan α=3,此时,sin α·tan α=-32.所以sin α·tan α=-32.(2)设θ是第三象限角,且|cosθ2|=-cos θ2,则θ2是()A .第一象限角B .第二象限角C .第三象限角D .第四象限角答案B解析由θ是第三象限角知,θ2为第二或第四象限角,∵|cos θ2|=-cos θ2,∴cos θ2<0,综上可知,θ2为第二象限角.命题点2三角函数线例3(1)满足cos α≤-12的角的集合是.答案|2k π+23π≤α≤2k π+43π,k ∈Z 解析作直线x =-12交单位圆于C ,D 两点,连接OC ,OD ,则OC 与OD 围成的区域(图中阴影部分)即为角α终边的范围,故满足条件的角α的集合为|2k π+23π≤α≤2k π+43π,k ∈Z(2)若-3π4<α<-π2,从单位圆中的三角函数线观察sin α,cos α,tan α的大小关系是.答案sin α<cos α<tan α解析如图,作出角α的正弦线MP ,余弦线OM ,正切线AT ,观察可知sin α<cos α<tan α.思维升华(1)利用三角函数的定义,已知角α终边上一点P 的坐标可求α的三角函数值;已知角α的三角函数值,也可以求出点P 的坐标.(2)利用三角函数线解不等式要注意边界角的取舍,结合三角函数的周期性写出角的范围.跟踪训练2(1)(2018·济南模拟)已知角α的终边经过点(m ,-2m ),其中m ≠0,则sin α+cosα等于()A .-55B .±55C .-35D .±35答案B解析∵角α的终边经过点(m ,-2m ),其中m ≠0,∴m >0时,sin α=-2m 5m =-25cos α=m 5m =15,∴sin α+cos α=-55;m <0时,sin α=-2m -5m =25,cos α=m -5m =-15,∴sin α+cos α=55;∴sin α+cos α=±55,故选B.(2)在(0,2π)内,使得sin x >cos x 成立的x 的取值范围是()答案C解析当x ∈π2,sin x >0,cos x ≤0,显然sin x >cos x 成立;当x ,π4时,如图,OA 为x 的终边,此时sin x =|MA |,cos x =|OM |,sin x ≤cos x ;当xOB 为x 的终边,此时sin x =|NB |,cos x =|ON |,sin x >cos x .同理当x ∈πsin x >cosx ;当x ∈5π4,sin x ≤cos x ,故选C.1.下列说法中正确的是()A .第一象限角一定不是负角B .不相等的角,它们的终边必不相同C .钝角一定是第二象限角D .终边与始边均相同的两个角一定相等答案C解析因为-330°=-360°+30°,所以-330°角是第一象限角,且是负角,所以A 错误;同理-330°角和30°角不相等,但它们终边相同,所以B 错误;因为钝角的取值范围为(90°,180°),所以C 正确;0°角和360°角的终边与始边均相同,但它们不相等,所以D 错误.2.已知扇形的周长是6,面积是2,则扇形的圆心角的弧度数是()A .1B .4C .1或4D .2或4答案C解析设扇形的半径为r ,弧长为l ,+l =6,=2,=1,4=2,2.从而α=l r =41=4或α=l r =22=1.3.(2018·石家庄调研)已知角θ的终边经过点P (4,m ),且sin θ=35,则m 等于()A .-3B .3C.163D .±3答案B 解析sin θ=m16+m 2=35,且m >0,解得m =3.4.点P 从(1,0)出发,沿单位圆逆时针方向运动2π3弧长到达Q 点,则Q 点的坐标为()-12,-32,--12,--32,答案A解析点P 旋转的弧度数也为2π3,由三角函数定义可知Q 点的坐标(x ,y )满足x =cos 2π3=-12,y =sin 2π3=32.5.若sin θ·cos θ>0,sin θ+cos θ<0,则θ在()A .第一象限B .第二象限C .第三象限D .第四象限答案C解析∵sin θ·cos θ>0,∴sin θ>0,cos θ>0或sin θ<0,cos θ<0.当sin θ>0,cos θ>0时,θ为第一象限角,当sin θ<0,cos θ<0时,θ为第三象限角.∵sin θ+cos θ<0,∴θ为第三象限角.故选C.6.sin 2·cos 3·tan 4的值()A .小于0B .大于0C .等于0D .不存在答案A解析∵sin 2>0,cos 3<0,tan 4>0,∴sin 2·cos 3·tan 4<0.7.已知角α的终边过点P (-8m ,-6sin 30°),且cos α=-45,则m 的值为()A .-12B .-32C.12D.32答案C解析由题意得点P (-8m ,-3),r =64m 2+9,所以cos α=-8m64m 2+9=-45,解得m =±12,又cos α=-45<0,所以-8m <0,即m >0,所以m =12.8.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;④若sin α=sin β,则α与β的终边相同;⑤若cos θ<0,则θ是第二或第三象限的角.其中正确命题的个数是()A .1B .2C .3D .4答案A解析举反例:第一象限角370°不小于第二象限角100°,故①错;当三角形的内角为90°时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于sinπ6=sin 5π6,但π6与5π6的终边不相同,故④错;当cos θ=-1,θ=π时,其既不是第二象限角,也不是第三象限角,故⑤错.综上可知,只有③正确.9.若圆弧长度等于该圆内接正方形的边长,则其圆心角的弧度数是.答案2解析设圆半径为r ,则圆内接正方形的对角线长为2r ,∴正方形边长为2r ,∴圆心角的弧度数是2rr= 2.10.若角α的终边与直线y =3x 重合,且sin α<0,又P (m ,n )是角α终边上一点,且|OP |=10,则m -n =.答案2解析由已知tan α=3,∴n =3m ,又m 2+n 2=10,∴m 2=1.又sin α<0,∴m =-1,n =-3.故m -n =2.11.已知角α的终边上一点P 2π3,cos α的最小正值为.答案11π6解析由题意知,点r =1,所以点P 在第四象限,根据三角函数的定义得cos α=sin2π3=32,故α=2k π-π6(k ∈Z ),所以α的最小正值为11π6.12.函数y =sin x -32的定义域为.答案2k π+π3,2k π+23π,k ∈Z 解析利用三角函数线(如图),由sin x ≥32,可知2k π+π3≤x ≤2k π+23π,k ∈Z .13.已知角α的终边在如图所示阴影表示的范围内(不包括边界),则角α用集合可表示为.答案α|2k π+π4<α<2k π+56π,k ∈Z 解析∵在[0,2π)内,终边落在阴影部分角的集合为π4,56π∴α|2k π+π4<α<2k π+56π,k ∈Z14.若角α的终边落在直线y =3x 上,角β的终边与单位圆交于点12,m,且sin α·cos β<0,则cos α·sin β=.答案±34解析由角β12,m cos β=12sin α·cos β<0知,sin α<0,因为角α的终边落在直线y =3x 上,所以角α只能是第三象限角.记P 为角α的终边与单位圆的交点,设P (x ,y )(x <0,y <0),则|OP |=1(O 为坐标原点),即x 2+y 2=1,又由y =3x 得x =-12,y =-32,所以cos α=x =-12,因为点12,m 12+m 2=1,解得m =±32,所以sin β=±32,所以cos α·sin β=±34.15.《九章算术》是我国古代数学成就的杰出代表作,其中“方田”章给出了计算弧田面积时所用的经验公式,即弧田面积=12×(弦×矢+矢2).弧田(如图1)由圆弧和其所对弦围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为2π3,半径为3米的弧田,如图2所示.按照上述经验公式计算所得弧田面积大约是平方米.(结果保留整数,3≈1.73)答案5解析如题图2,由题意可得∠AOB =2π3,OA =3,所以在Rt △AOD 中,∠AOD =π3,∠DAO =π6,OD =12AO =12×3=32,可得CD =3-32=32,由AD =AO ·sin π3=3×32=332,可得AB =2AD =2×332=3 3.所以弧田面积S =12(弦×矢+矢2)=12×33×32+=943+98≈5(平方米).16.如图,A ,B 是单位圆上的两个质点,点B 的坐标为(1,0),∠BOA =60°.质点A 以1rad /s 的角速度按逆时针方向在单位圆上运动,质点B 以2rad/s 的角速度按顺时针方向在单位圆上运动.(1)求经过1s 后,∠BOA 的弧度;(2)求质点A ,B 在单位圆上第一次相遇所用的时间.解(1)经过1s 后,质点A 运动1rad ,质点B 运动2rad ,此时∠BOA 的弧度为π3+3.(2)设经过t s 后质点A ,B 在单位圆上第一次相遇,则t (1+2)+π3=2π,解得t =5π9,即经过5π9s后质点A ,B 在单位圆上第一次相遇.。
三角函数考试内容:角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式:sin 2α+cos 2α=1sinα/cosα=tanαtanαcotα=1 正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx+φ)的图像.正切函数的图像和性质.已知三角函数值求角.正弦定理.余弦定理.斜三角形解法.考试要求: (1)理解任意角的概念、弧度的意义.能正确地进行弧度与角度的换算. (2)掌握任意角的正弦、余弦、正切的定义.了解余切、正割、余割的定义.掌握同角三角函数的基本关系式.掌握正弦、余弦的诱导公式.了解周期函数与最小正周期的意义. (3)掌握两角和与两角差的正弦、余弦、正切公式.掌握二倍角的正弦、余弦、正切公式. (4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明. (5)了解正弦函数、余弦函数、正切函数的图像和性质,会用"五点法"画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A ,ω,φ的物理意义. (6)会由已知三角函数值求角,并会用符号arcsinx 、arccosx 、arctanx 表示. (7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形.三角函数的概念一、 知识回顾1、角的概念:角的形成,角的始边,终边,顶点.2、正角;负角;零角.3、终边相同的角:与α角终边相同的角的集合(连同α角在内),可以记为{ββ|=k ·360+α,k ∈Z }.4、象限角:顶点在原点,始边与x 轴非负半轴重合,则终边落在第几象限,就称这个角是第几象限的角.5、(请写出各象限角的集合及各轴线角的集合 )6、区间角、区间角的集合:角的量数在某个确定的区间内(上),这角就叫做某确定区间的角.由若干个区间构成的集合称为区间角的集合.7、角度制: 8、弧度制:9、弧度与角度互换公式: 1rad =π180°≈57.30°=57°18ˊ. 1°=180π≈0.01745(rad )10、弧长公式:r l ⋅=||α. 扇形面积公式:211||22s lr r α==⋅扇形11、三角函数:设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y )P 与原点的距离为r ,则 ry =αsin ; rx =αcos ; xy =αtan ;yx =αcot ; xr =αsec ;. yr =αcsc .12、三角函数在各象限的符号:(一全二正弦,三切四余弦)13、三角函数线正弦线:MP; 余弦线:OM; 正切线: AT. 二、 基本训练1、集合},42|{Z k k x x M ∈+==ππ,},24|{Z k k x x N ∈+==ππ,则( )A 、N M =B 、N M ⊃C 、N M ⊂D 、Φ=N M2、若α是第二象限角,则2α是第_____象限角,2α的范围是________________,απ-2是第_____象限角。
三角函数复习专题一、核心知识点归纳:★★★1、正弦函数、余弦函数和正切函数的图象与性质:★★2.正、余弦定理:在ABC ∆中有: ①正弦定理:2sin sin sin a b cR A B C===R 为ABC ∆外接圆半径2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩ ⇒ sin 2sin 2sin 2a A R b B R c C R ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式:111sin sin sin 222ABC S abs C ac B bc A ∆===③余弦定理: 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩三、例题集锦: 考点一:三角函数的概念1.如图,设A 是单位圆和x 轴正半轴的交点,Q P 、是 单位圆上的两点,O 是坐标原点,6π=∠AOP ,[)παα,0,∈=∠AOQ .1若34(,)55Q ,求⎪⎭⎫⎝⎛-6cos πα的值;2设函数()f OP OQ α=⋅,求()αf 的值域. 2.已知函数2()22sin f x x x =-.Ⅰ若点(1,P在角α的终边上,求()f α的值; Ⅱ若[,]63x ππ∈-,求()f x 的值域.考点二:三角函数的图象和性质3.函数()sin()(0,0,||)2f x A x A ωφωφπ=+>><部分图象如图所示.Ⅰ求()f x 的最小正周期及解析式;Ⅱ设()()cos 2g x f x x =-,求函数()g x 在区间[0,]x π∈上的最大值和最小值.考点三、四、五:同角三角函数的关系、 诱导公式、三角恒等变换4.已知函数x x x f 2cos )62sin()(+-=π.1若1)(=θf ,求θθcos sin ⋅的值;2求函数)(x f 的单调增区间.3求函数的对称轴方程和对称中心 5.已知函数2()2sin cos 2cos f x x x x ωωω=-0x ω∈>R ,,相邻两条对称轴之间的距离等于2π.Ⅰ求()4f π的值;Ⅱ当 02x π⎡⎤∈⎢⎥⎣⎦,时,求函数)(x f 的最大值和最小值及相应的x 值. 6、已知函数2()2sin sin()2sin 12f x x x x π=⋅+-+ ()x ∈R . Ⅰ求函数()f x 的最小正周期及函数()f x 的单调递增区间;Ⅱ若0()23x f =,0ππ(, )44x ∈-,求0cos 2x 的值.7、已知πsin()410A +=,ππ(,)42A ∈. Ⅰ求cos A 的值; Ⅱ求函数5()cos 2sin sin 2f x x A x =+的值域.考点六:解三角形8.已知△ABC 中,2sin cos sin cos cos sin A B C B C B =+. Ⅰ求角B 的大小;Ⅱ设向量(cos , cos 2)A A =m ,12(, 1)5=-n ,求当⋅m n 取最 小值时,)4tan(π-A 值.9.已知函数23cos sin sin 3)(2-+=x x x x f ()R x ∈. Ⅰ求)4(πf 的值;Ⅱ若)2,0(π∈x ,求)(x f 的最大值;Ⅲ在ABC ∆中,若B A <,21)()(==B f A f ,求AB BC 的值.10、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b Ba A-=. Ⅰ求角A 的大小;Ⅱ若a =求△ABC 面积的最大值.11、 在△ABC 中,a ,b ,c 分别为内角A ,B ,C 的对边,且b 2+c 2-a 2=bc .9第题图Ⅰ求角A 的大小;Ⅱ设函数2cos 2cos 2sin 3)(2x x xx f +=,当)(B f 取最大值23时,判断△ABC 的形状.12、在ABC ∆中,内角A 、B 、C 所对的边分别为,,a b c ,已知1tan 2B =,1tan 3C =,且1c =. Ⅰ求tan A ; Ⅱ求ABC ∆的面积.13、在ABC ∆中,角A ,B ,C 所对应的边分别为a ,b ,c ,且274sin cos222A B C +-=. Ⅰ求角C 的大小; Ⅱ求sin sin A B +的最大值.高三文科---三角函数专题11.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos2θ=A .45- B .35- C .35 D .452.如图,质点P 在半径为2的圆周上逆时针运动,其初始位置为)2,2(0-P ,角速度为1,那么点P 到x 轴距离d 关于时间t 的函数图象大致为3.动点(),A x y 在圆221x y +=上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间0t =时,点A 的坐标是13(,)22,则当012t ≤≤时,动点A 的纵坐标y 关于t 单位:秒的函数的单调递增区间是A 、[]0,1B 、[]1,7C 、[]7,12D 、[]0,1和[]7,124.函数f (x)Asin(wx ),(A,w,=+φφ)为常数,)0,0>>w A 的部分图象如图所示,则f (0)____的值是5.已知函数f (x)A tan(x )=ω+ϕω>0,2π<ϕ,y f (x)=的部分图象如下图,则f24π=__________. 6. 函数f x=sinx -cosx +6π的值域为A . -2 ,2B .33C .-1,1D .-33 8.已知函数()sin(2)f x x ϕ=+,其中ϕ为实数,若()()6f x f π≤对x R ∈恒成立,且()()2f f ππ>,则()f x 的单调递增区间是 A ,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C 2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ D ,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦14.定义在⎪⎭⎫⎝⎛20π,的函数y=6cosx 图像与y=5tanx 图像的交点为P,过点P 作PP 1⊥x轴于点P 1,直线PP 1与y=sinx 的图像交于点P 2,则线段P 1P 2的长为 .16.如图,四位同学在同一个坐标系中分别选定了一个适当的区间,各自作出三个函数sin 2y x =, sin()6y x π=+,sin()3y x π=-的图像如下,结果发现其中有一位同学作出的图像有错误,那么有错误..的图像是 A B C D17.已知0ω>,函数()sin()4f x x πω=+在(,)2ππ上单调递减.则ω的取值范围是20.设sin 1+=43πθ(),则sin 2θ=A 79- B 19- C 19 D 7922.已知,2)4tan(=+πx 则x x2tan tan 的值为__________25.若tan θ+1tan θ=4,则sin 2θ=A .15B . 14C . 13D . 1226.已知α为第二象限角,33cos sin =+αα,则cos2α=A 555527.若02πα<<,02πβ-<<,1cos ()43πα+=,3cos ()42πβ-=则cos ()2βα+= A33 B 33-53 D 628. 设α为锐角,若4cos 65απ⎛⎫+= ⎪⎝⎭,则)122sin(π+a 的值为 . 29.在△ABC 中,角A 、B 、C 所对应的边为c b a ,,1若,cos 2)6sin(A A =+π 求A 的值;2若c b A 3,31cos ==,求C sin 的值.30.如图,△ABC 中,AB=AC=2,BC=3点D 在BC 边上,∠ADC=45°,则AD 的长度等于___.31.在ABC ∆中,内角A,B,C 所对的边分别是c b a ,,,已知8b=5c,C=2B,则cosC=A257 B 257- C 257± D 2524 34.设ABC ∆的内角,,A B C 的对边分别为,,a b c ,且53cos =A ,135cos =B ,3=b 则c =35. 如图,正方形ABCD 的边长为1,延长BA 至E ,使1AE =,连接EC 、ED 则sin CED ∠=A 、31010 B 、1010 C 、510 D 、51536. 在ABC ∆中,角,,A B C 所对边长分别为,,a b c , 若2222a b c +=,则cos C 的最小值为A .3. 22C . 12D . 12-37.在ABC 中,60,3B AC ==则2AB BC +的最大值为 . 39. 设ABC ∆的内角,,A B C 所对的边为,,a b c ;则下列命题正确的是①若2ab c >;则3C π<②若2a b c +>;则3C π<③若333a b c +=;则2C π<④若()2a b c ab +<;则2C π>⑤若22222()2a b c a b +<;则3C π>43. 已知函数()tan(2),4f x x =+πⅠ求()f x 的定义域与最小正周期;II 设0,4⎛⎫∈ ⎪⎝⎭πα,若()2cos 2,2f =αα求α的大小45. 设函数22())sin 4f x x x π=++. I 求函数()f x 的最小正周期;II 设函数()g x 对任意x R ∈,有()()2g x g x π+=,且当[0,]2x π∈时, 1()()2g x f x =-,求函数()g x 在[,0]π-上的解析式.47.设426f (x )cos(x )sin x cos x π=ω-ω+ω,其中.0>ω Ⅰ求函数y f (x )= 的值域Ⅱ若y f (x )=在区间322,ππ⎡⎤-⎢⎥⎣⎦上为增函数,求 ω的最大值.48. 函数2()6cos 33(0)2xf x x ωωω=->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形.Ⅰ求ω的值及函数()f x 的值域; Ⅱ若083()f x =,且0102(,)33x ∈-,求0(1)f x +的值. 52. 已知,,a b c 分别为ABC ∆三个内角,,A B C 的对边,cos 3sin 0a C a C b c --= 1求A ; 2若2a =,ABC ∆的面积为3;求,b c .53.在∆ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5C .Ⅰ求tan C 的值; Ⅱ若a 2求∆ABC 的面积.54.在△ABC中,角A ,B ,C 的对边分别为a ,b ,c .已知,sin()sin()444A b C cB a πππ=+-+= 1求证: 2B C π-=2若2a =,求△ABC 的面积.56.已知向量(cos sin ,sin )x x x ωωω=-a ,(cos sin ,23cos )x x x ωωω=--b ,设函数()f x λ=⋅+a b ()x ∈R 的图象关于直线πx =对称,其中ω,λ为常数,且1(,1)2ω∈.Ⅰ求函数()f x 的最小正周期;Ⅱ若()y f x =的图象经过点π(,0)4,求函数()f x 在区间3π[0,]5上的取值范围. 57.在ABC ∆中,已知3AB AC BA BC =. 1求证:tan 3tan B A =; 2若5cos 5C =,求A 的值.58. 已知△ABC 得三边长成公比为2的等比数列,则其最大角的余弦值为_____.59.已知ABC ∆ 的一个内角为120o ,并且三边长构成公差为4的等差数列,则ABC ∆的面积为_______60.已知等比数列{a n }的公比q=3,前3项和313.3S = I 求数列{a n }的通项公式;II 若函数()sin(2)(0,0)f x A x A p ϕϕπ=+><<<在6x π=处取得最大值,且最大值为a 3,求函数fx 的解析式.63.函数22xy sin x =-的图象大致是 64.函数fx=sin x ωϕ+的导函数()y f x '=的部分图像如图4所示,其中,P 为图像与y 轴的交点,A,C 为图像与x 轴的两个交点,B 为图像的最低点.1若6πϕ=,点P 的坐标为0,332,则ω= ; 2求∆ABC 面积65设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.I 求BII 若1sin sin 4A C =,求C .66在△ABC 中,内角A 、B 、C 的对边分别是a 、b 、c ,且222a b c =++.Ⅰ求A ;Ⅱ设a =S 为△ABC 的面积,求3cos cos S B C +的最大值,并指出此时B 的值.67在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且3cos()cos sin()sin()5A B B A B A c ---+=-.Ⅰ求sin A 的值;Ⅱ若a =5b =,求向量BA 在BC 方向上的投影68已知函数()sin cos f x x a x =+的一个零点是3π4. Ⅰ求实数a 的值;Ⅱ设22()[()]2sin g x f x x =-,求()g x 的单调递增区间.69在△ABC 中,内角,,A B C 所对的边分别为,,a b c ,已知sin (tan tan )tan tan B A C A C +=.Ⅰ求证:,,a b c 成等比数列; Ⅱ若1,2a c ==,求△ABC 的面积S .三角函数1、在ABC ∆中,已知内角3A π=,边BC =设内角B x =,面积为y .1求函数()y f x =的解析式和定义域; 2求y 的最大值.2、已知a =coos α,sin α,b =coos β,sin β,其中0<α<β<π. 1求证:a +b 与a -b 互相垂直;2若k a +b 与a -k b 的长度相等,求β-α的值k 为非零的常数.3、已知3sin22B A ++cos 22BA -=2, cocacobs ≠0,求tanAtanB 的值; 5、已知ABC ∆中,1||=AC ,0120=∠ABC ,θ=∠BAC ,记→→•=BC AB f )(θ, 1求)(θf 关于θ的表达式; 2求)(θf 的值域;6、已知向量],2[),2cos ),122(cos(),2cos ),122(sin(ππππ∈-+=+=x x x b x x a ,函数b a x f ⋅=)(.I 若53cos -=x ,求函数)(x f 的值;II 将函数)(x f 的图象按向量c =)0)(,(π<<m n m 平移,使得平移后的图象关于原点对称,求向量c .9、在ABC ∆中,已知内角A 、B 、C 所对的边分别为a 、b 、c,向量(2sin ,m B =,2cos 2,2cos 12B n B ⎛⎫=- ⎪⎝⎭,且//m n ;I 求锐角B 的大小;II 如果2b =,求ABC ∆的面积ABC S ∆的最大值; 10、已知向量()()3cos2,1,1,sin2,,m a x n b a x a b R ==-∈,集合{}2cos ,22M x x x ππ⎡⎤=∈-⎢⎥⎣⎦,若函数()f x m n x M =∈在时,取得最大值3,最小值为-1,求实数,a b 的值16、在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且.cos cos 3cos B c B a C b -= I 求cos B 的值;II 若2=⋅BC BA ,且22=b ,求c a 和b 的值.21、已知向量m =()B B cos 1,sin -, 向量n = 2,0,且m 与n 所成角为错误!,其中A 、B 、C 是ABC ∆的内角;ABC1201求角B 的大小;2求 C A sin sin +的取值范围;26、在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,C =2A,43cos =A , 1求B C cos ,cos 的值;2若227=⋅BC BA ,求边AC 的长; 30、已知ABC △的面积为3,且满足60≤⋅≤AC AB ,设AB 和AC 的夹角为θ. I 求θ的取值范围;II 求函数)4(sin 2)(2πθθ+=f -θ2cos 3的最大值与最小值.33、已知△ABC 的面积为3,且06,AB AC AB AC θ→→→→≤•≤设和的夹角为; 1求θ的取值范围;2求函数22()(sin cos )f θθθθ=+-的最大值和最小值; 36、已知A B 、是△ABC 的两个内角,向量2cos, sin 22A B A Ba +-=(),若6||2a =. Ⅰ试问B A tan tan ⋅是否为定值若为定值,请求出;否则请说明理由; Ⅱ求C tan 的最大值,并判断此时三角形的形状. 38、在△ABC 中,已知35=BC ,外接圆半径为5. Ⅰ求∠A 的大小; Ⅱ若ABC AC AB ∆=⋅,求211的周长. 40、如图A 、B 是单位圆O 上的点,C 是圆与x 轴正半轴的交点,A 点的坐标为)54,53(,三角形AOB 为正三角形. Ⅰ求COA ∠sin ;Ⅱ求2||BC 的值.45、已知函数fx=4sin 24π42x ππ≤≤1求)(x f 的最大值及最小值;2若不等式|fx -m|<2恒成立, 求实数m 的取值范围49、已知函数fx =·,其中=sin ωx +cos ωx,错误!cos ωx,=cos ωx -sin ωx,2sin ωx ω>0,若fx 相邻的对称轴之间的距离不小于错误!. 1求ω的取值范围;2在△ABC 中,a,b,c 分别为A,B,C 的对边,a =错误!,b+c =3,当ω最大时,fA =1,求△ABC 的面积.56、已知角C B A ,,为ABC ∆的三个内角,其对边分别为c b a ,,,若)2sin ,2cos (A A -=m ,)2sin ,2(cos A A =n ,32=a ,且21=⋅n m .1若ABC ∆的面积3=S ,求c b +的值. 2求c b +的取值范围.59、在锐角△ABC 中,已知内角A 、B 、C 所对的边分别为a 、b 、c ,且tanA -tanB=1+tanA ·tanB .1若a 2-ab =c 2-b 2,求A 、B 、C 的大小;2已知向量m =sinA,cosA,n =cosB,sinB,求|3m -2n |的取值范围.62、已知函数0)6(,cos sin cos 2)(2=+=πf x x a x x f1求函数)(x f 的最小正周期及单调增区间;2若函数)(x f 的图象按向量)1,6(-=πm 平移后得到函数)(x g 的图象,求)(x g 的解析式.64、设向量)2,(),,0(),0,1(),sin ,cos 1(),sin ,cos 1(ππβπαββαα∈∈=-=+=c b a ,2sin,3,,2121βαπθθθθ-=-求且的夹角为与的夹角为与c b c a 的值;68已知A 、B 、C 为ABC ∆的三个内角,向量65(,cos )22A B A B +-=a ,且3|| 5.5=a 1求tan tan A B 的值;2求C 的最大值,并判断此时ABC ∆的形状.74、在△ABC 中,,0),1,(),cos ,sin 3(),2cos ,(cos πλ≤≤--x C x x B x x A 若△ABC 的重心在y 轴负半轴上,求实数λ的取值范围.76、在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若).(R k k BC BA AC AB ∈=⋅=⋅ Ⅰ判断△ABC 的形状; Ⅱ若k c 求,2=的值.77、在△ABC 中,a 、b 、c 分别是角A 、B 、C 的对边,且cos cos B C ba c=-+2. I 求角B 的大小;II 若b a c =+=134,,求△ABC 的面积.78、已知ABC ∆中,a 、b 、c 是三个内角A 、B 、C 的对边,关于x 的不等式2cos 4sin 60x C x C ++<的解集是空集. 1求角C 的最大值;2若72c =,ABC ∆的面积S =求当角C 取最大值时a b +的值. 84、在△ABC 中,角A ,B ,C 所对边分别为a ,b ,c ,且tan 21tan A c Bb+=. Ⅰ求角A ; Ⅱ若m (0,1)=-,n ()2cos ,2cos 2C B =,试求|m +n |的最小值. 90、已知锐角△ABC 三个内角为A 、B 、C,向量22sin ,cos sin pA A A 与向量sin cos ,1sin qA A A 是共线向量.Ⅰ求角A. Ⅱ求函数232sin cos 2C By B 的最大值.96、已知]),0[,0)(cos()(πωωπ∈Φ>Φ+=x x f 是R 上的奇函数,其图像关于直线43=x 对称,且在区间]41,41[-上是单调函数,求ω和Φ的值; 98、已知向量(1tan ,1),(1sin 2cos 2,3)x x x =-=++-b a ,记().f x =⋅b a1求fx 的值域及最小正周期;2若224f f ααπ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭其中0,2πα⎛⎫∈ ⎪⎝⎭,求角.α。
高考数学总复习 三角函数的概念一、角的概念:1、 角的定义:角可以看作平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。
旋转开始时的射线叫角的始边;旋转终止时的射线叫角的终边;射线的端点叫角的顶点。
2、 角的分类:按逆时针方向旋转形成的角叫正角;按顺时针方向旋转形成的角叫负角;若一条射线没有任何旋转,称他形成一个零角。
3、 终边相同的角:所有与α终边相同的角,连同角α在内,可以构成一个集合{}z k k s ∈⋅+==,360|0αββ即任一终边相同的角,都可以表示成角整个周角的和.二、 角的度量:1、 角度制:规定周角的3601为1度的角,这种用度作为单位来度量角的单位制叫做角度制。
角度的单位符号是“o ”,读做度。
2、 弧度制:把长度等于半径长的弧所对的圆心角叫做1弧度的角。
弧度的单位符是:“rad ”,读做 弧度。
3、 角度化为弧度公式:3600=π2rad ;π=1800rad ;01745.018010≈=πrad. 4、 弧度制化为角度制公式:36020=rad π;1800=rad π;30.57)180(001≈=πrad 。
特别注意:在我们解题时,同一个角的表示之中不能同时出现角度和弧度,即不要“一题两制”,最好按照要求,顺其自然。
5、 扇形弧长公式:r l α=; 180r l n π=。
6、 扇形面积公式:r lr s 22121α==;3602r n s π=。
三、任意角的三角函数:1、 三角函数的定义:设α是任意的一个角,在角的终边上任取一个点P(除端点),设其坐标为P(x,y),它与原点的距离为r (02222>=+=+y y x x r ),则 (1) 比值r y 叫做角α的正弦,记作sin α 即sin α =r y . (2) 比值r x 叫做角α的余弦,记作cos α 即cos α =r x . (3) 比值x y 叫做角α的正切,记作tan α 即tan α=x y . (4) 比值y x 叫做角α的余切,记作cot α 即cot α=y x . (5) 比值x r 叫做角α的正割,记作sec α 即sec α=x r . (6) 比值y r 叫做角α的正弦,记作csc α 即csc α=yr . 注:正弦、余弦、正切、余切、正割、余割分别可看成是从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,这六个函数统称为三角函数。