第八章三维形体的表示

三维形的认识与分类在我们日常生活中，我们所接触到的事物都有不同的形状。

有些形状是平面的，只有长度和宽度，称为二维形状，比如圆形和矩形；而还有一些形状则有长度、宽度和高度，称为三维形状，比如立方体和圆柱体。

本文将探讨三维形状的认识与分类。

对于三维形状的认识，我们首先需要了解什么是三维空间。

三维空间是指具有长度、宽度和高度三个方向的空间，如一个立方体，它的六个面都是平面，分别代表了不同的方向。

在三维空间中，物体可以以各种不同的方式排列和组合，形成各种不同的三维形状。

分类三维形状的方法主要有两种：根据表面特征分类和根据构成要素分类。

根据表面特征分类，我们可以将三维形状分为以下几类：1. 球体：球体是一种完全由曲面构成的三维形状，它的表面到圆心的距离处处相等。

例如，地球就是一个近似于球体的天体。

球体具有无数个不同的半径，因此可以分为不同大小的球体。

2. 圆柱体：圆柱体是一种由两个平行的圆面和连接两个圆面的侧面组成的三维形状。

圆柱体的侧面是一个矩形，两个圆面的圆心在同一直线上。

例如，一根筒状的笔就是一个近似于圆柱体的物体。

3. 圆锥体：圆锥体是一种由一个圆面和连接圆面和圆心的侧面组成的三维形状。

侧面是一条从圆心到圆周的曲线。

如果圆锥体的底面是正圆，则称为正圆锥体；如果底面是椭圆，则称为椭圆锥体。

4. 立方体：立方体是一种具有六个面，每个面都是一个正方形的三维形状。

立方体的六个面互相平行，并且相邻的两个面之间的距离相等。

例如，一个骰子就是一个近似于立方体的物体。

根据构成要素分类，我们可以将三维形状分为以下几类：1. 多面体：多面体是一种由多个平面构成的立体物体。

它的边界由多个面、边和顶点组成。

例如，正方体和六面体都是多面体。

2. 曲面体：曲面体是指由曲面构成的立体物体，其表面没有平面。

曲面体可以是球体、圆柱体、圆锥体等。

曲面体在数学和几何中有着重要的应用。

虽然三维形状的分类方法多种多样，但通过了解不同的分类方法，我们可以更好地认识和理解各种立体物体的特征和属性。

三维形的投影了解俯视和立体的表示方法投影是对于三维形的表达方法，通过将三维形投射到二维平面上来呈现其形状和结构。

在投影的过程中，俯视图和立体图是两种常用的表示方法。

本文将介绍三维形的投影，包括俯视图和立体图的含义、表达方法以及其在不同领域的应用。

一、俯视图的表达方法俯视图是指从上方向下看的视角，类似于鸟瞰图。

在俯视图中，三维形的上、前、后、左、右等各个方向的轮廓都能够清晰地展现出来，同时可以准确表达三维形各个部分之间的关系。

俯视图的表达方法有几种常见的方式：1. 平面投影法：将三维形放置在平面上，然后从上方垂直向下投影，得到的投影图即为俯视图。

这种方法通常用于制图和建筑设计中，能够准确地表示尺寸和比例。

2. 效果图法：在计算机图形学中，可以通过三维建模软件将三维形转化为俯视图的效果图。

这种表达方法更加直观生动，适用于室内设计、游戏开发等领域。

二、立体图的表达方法立体图是指通过投影方法将三维形体现在二维平面上的一种图形表达方式。

与俯视图不同，立体图可以呈现三维形的各个侧面，更加贴合实际物体。

立体图的表达方法有几种常见的方式：1. 正射投影法：通过将不同侧面的立体形分别投影到垂直的平面上，再将各个投影图进行组合，得到整个立体图。

这种方法常用于工程制图和机械设计中，能够准确地表示尺寸和形状。

2. 透视投影法：透视投影法是一种能够表现三维效果的投影方法，在绘画和建筑设计中广泛应用。

通过透视原理，在二维平面上用特定的透视点和透视线来表达三维形的立体感，使观者能够感受到深度和空间关系。

三、俯视图和立体图的应用俯视图和立体图作为三维形投影的主要表达方法，在多个领域中得到广泛应用。

1. 建筑设计与室内设计：在建筑设计与室内设计过程中，用俯视图和立体图能够清晰地展示整体规划、空间布局、材质效果等信息，帮助设计师和客户更好地理解和沟通设计意图。

2. 工程制图与机械设计：在工程制图和机械设计中，用俯视图和立体图能够准确地表示物体尺寸、形状和结构，为制造、加工等工艺提供依据。

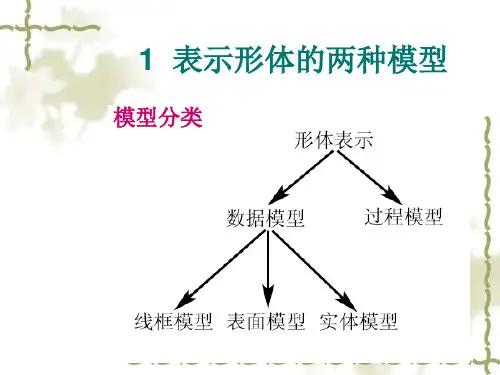
三维对象表示方法三维实体描述方法：1.边界表示 多边形表面2.空间区分 立体构造 八叉树 分形多边形表面：几何表：顶点坐标和用来标识多边形表面空间方向的参数点表 边表 面表欧拉公式：V-E+S=2（V 为顶点数，E 为棱线数，S 为面数）凡是满足欧拉公式的形体均称为欧拉形体属性表：指明物体透明度及表面反射度的参数和纹理特征曲线曲面：样条曲线/面：样条曲线：通过一组指定点集而生成的平滑曲线的柔性带；样条曲面：可以使用两组正交样条曲线进行描述；、y K y y y K ''≈<<''+''=,1|:|when )1(232曲率公式：曲线不同要求：0阶连续 1阶连续 2阶连续Bezier 样条：N+1个控制点 控制点P k =(x k ,y k ,z k ) 混合函数∑==n k n k k u B P u P 0,)()(P K :控制点位置向量B k,n (u) = C(n,k) * u k * (1-u)n-kC(n,k) = n! / (k!(n-k)!)实体构造：由简单物体构成复杂物体1. 扫描表示：基于一个元素(点、线、面等)或一个形体沿指定路径运动而生成的新的形体2. 结构实体几何法：通过两个指定物体间的并、交、差等集合操作而生成新的物体八叉树8叉树的表示应用三维形体的分解.它对一个外接三维立方体进行递归分解；直至所有小立方体单元要么全部均质，要么全部空，或已分解到规定的分解精度为止。

分形几何方法基本特征1.每点处无限细节2.整体和部分的自相似性分数维：我们知道某些形状相同的几何体放在一起可以组成一个较大的它们的复制品。

例如，需要2条相同的线段（1维的）组成长度扩大到两倍的一条线段。

需要4个相同的正方形（2维几何体）组成棱长扩大到两倍的一个正方形。

需要8个相同的正方体组成一个边长扩大到2倍的一个正方体。

一般的，需要2^d个相同的d维超立方体组成边长扩大到两倍的一个大的d维超立方体；需要c=a^d个相同的几何体组成一个边长扩大a倍的大复制品。

三维形的认识与分类（小学四年级数学）三维形的认识与分类在小学四年级的数学学习中，我们将开始学习有关几何图形的知识。

今天，我们将重点学习三维形的认识与分类。

一、认识三维形三维形是指具有长度、宽度和高度三个方向的物体。

在我们的日常生活中，我们可以看到很多三维形，例如立体电视、立方体的骰子、圆柱形的水杯等。

这些物体都具有不同的形状和特征，让我们来仔细观察它们。

1. 球体球体是一种特殊的三维形，它的表面是平滑且没有棱角的。

我们可以想象成一个完全由圆形组成的立体。

常见的球体有篮球、足球、网球等。

它们都具有相同的特点，表面光滑且没有底面。

2. 圆柱体圆柱体由两个圆形和一条平行于两个圆形的直线相连而成。

它的侧面是曲面，底面是圆形。

我们可以举例来理解圆柱体，例如铅笔、水杯、香蕉等。

它们都具有两个圆形底面和一个曲面。

3. 立方体立方体是由六个正方形面构成的三维形。

它的六个面都是完全相同的正方形。

常见的立方体有骰子、盒子等。

它们的六个面都是正方形，边长相等。

4. 锥体锥体是由一个圆锥面和一个底面构成的三维形。

圆锥面是由一个尖顶点和与底面边缘连接的直线围成的。

我们可以想象成一个地面逐渐变窄的圆锥形。

常见的锥体有冰淇淋、棒棒糖等。

二、分类三维形了解了不同的三维形后，我们可以根据它们的特征进行分类。

1. 按底面形状分类根据底面的形状，我们可以将三维形分为圆柱体和四边形面的形状。

圆柱体的底面是圆形，而四边形面的形状可以是正方形或者矩形。

2. 按侧面的形状分类根据侧面的形状，我们可以将三维形分为直棱柱、倾斜棱柱和曲面棱锥。

直棱柱的侧面是长方形或正方形，而倾斜棱柱的侧面则是菱形或矩形。

曲面棱锥的侧面是曲面，例如冰淇淋锥形的尖尖部分。

通过对三维形的分类，我们可以更好地理解它们的特征和结构。

这将帮助我们在解决数学问题时更加准确地应用相应的几何概念。

三、小结在本篇文章中，我们学习了三维形的认识与分类。

通过认识不同的三维形，例如球体、圆柱体、立方体和锥体，并根据其特征进行分类，我们能更好地理解它们的结构和特点。

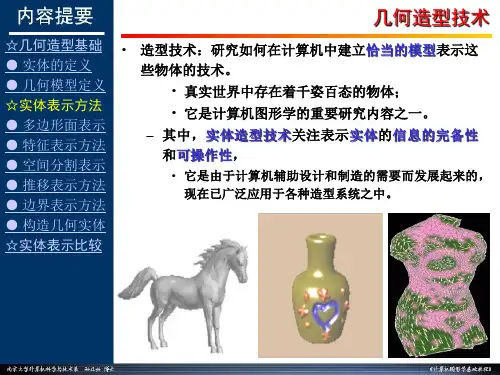
一、概述三维实体模型在计算机科学和工程领域中扮演着重要角色，它们被广泛应用在计算机辅助设计（CAD）、设计和制造（DM）以及虚拟现实（VR）等领域。

如何高效准确地表示和处理三维实体模型一直是学术界和工业界关注的重点问题之一。

本文将介绍计算机中三维实体模型的表示方法，包括多边形网格、B样条曲面、体素等，并探讨它们各自的优缺点及适用范围。

二、多边形网格表示方法1. 定义多边形网格是一种由顶点、边和面组成的三维几何体表示方法。

它由一组顶点坐标和连接这些顶点的三角形或四边形面构成。

多边形网格是三维实体模型最常见的表示方法之一，被广泛应用在图形学、动画和游戏开发等领域。

2. 优点（1）灵活性强：多边形网格能够表示各种形状的三维物体，并且可以对顶点进行细粒度的编辑和操作。

（2）易于渲染：多边形网格可以直接转换为计算机图形的基本单元，易于进行光栅化和渲染。

3. 缺点（1）表面光滑性差：多边形网格无法很好地表示曲面，对于表面光滑性要求较高的物体，需要增加顶点数目来逼近真实表面。

（2）内部结构不明显：多边形网格无法直观地表示三维实体的内部结构，例如对于固体模型的空洞或内部空间无法直接表达。

4. 应用多边形网格广泛应用于三维建模和可视化领域，如CAD软件、动画制作和游戏引擎等。

三、B样条曲面表示方法1. 定义B样条曲面是一种由B样条基函数线性组合而成的曲面表示方法。

它通过对控制顶点的位置进行调整，可以灵活地描述各种曲面形状，并且具有较好的表面光滑性和局部编辑能力。

2. 优点（1）表面光滑性好：B样条曲面可以较好地逼近真实曲面，并且能够实现G1、G2连续性的表面拟合。

（2）局部控制性强：B样条曲面的控制点可实现局部编辑，对整体形状的影响较小。

3. 缺点（1）复杂性高：B样条曲面的数学原理和计算方法较为复杂，实现和计算成本较高。

（2）内部结构不明显：类似于多边形网格，B样条曲面也无法直观地表示三维实体的内部结构。

4. 应用B样条曲面广泛应用于工程设计、汽车造型和工业设计等领域，如CATIA、Pro/E等三维设计软件。

三维形的认识与性质三维形是我们日常生活中常见的立体物体，它们具有一些特定的性质和特征。

通过对三维形的认识和了解，我们可以更好地理解和应用立体几何知识。

本文将从三维形的定义、特征、分类和性质等方面进行探讨。

一、三维形的定义三维形是指在三维空间中存在的具有长度、宽度和高度的几何体。

与二维形状相比，三维形是立体的，可以从不同的角度观察和描述。

常见的三维形包括立方体、球体、圆柱体、圆锥体等。

二、三维形的特征1. 长度、宽度和高度：三维形是由长度、宽度和高度构成的，这些特征使得三维形在空间中具有体积和形态上的差异。

2. 角度：三维形中的角度可以有不同的度量方式，例如直角、钝角和锐角。

3. 面和边：三维形具有面和边，通过面和边的组合可以构成不同形状的三维体。

三、三维形的分类根据形状和结构的不同，三维形可以分为以下几类：1. 柱状体：具有两个平行且相等的底面以及连接底面的侧面，如圆柱体和棱柱体。

2. 球状体：由所有离球心的点组成，如球体。

3. 圆锥体：具有一个圆形底面和一个点（称为顶点）连接底面的侧面，如圆锥体和棱锥体。

4. 立方体：具有六个相等的正方形面，如立方体。

5. 其他形状：还有许多其他的三维形状，如四面体、正八面体等。

四、三维形的性质1. 体积：三维形的体积用来描述立体物体所占据的空间大小。

不同形状的三维形体计算体积的方法也不同，例如球体的体积计算公式为V = (4/3)πr³，其中r为球体的半径。

2. 表面积：三维形的表面积指的是立体物体外表面的总面积。

不同形状的三维形体计算表面积的方法也不同，例如立方体的表面积计算公式为A = 6a²，其中a为立方体的边长。

3. 射影：三维形在二维平面上的射影称为立体的平行视图。

平行视图可以帮助我们更清楚地了解三维形的形状和结构。

4. 对称性：某些三维形具有对称面或对称轴，具有对称性的三维形在可视化和构造上更具美感和平衡感。

结论通过对三维形的认识与性质的探讨，我们可以更好地理解和应用立体几何知识。

三维形的认知与描述认知是人们对于外部世界的知觉和理解。

在我们的日常生活中，我们通过感官接收到的信息，然后对这些信息进行加工和理解。

而认知的一个重要方面就是对事物形状和结构的认知与描述。

在这篇文章中，我们将探讨关于三维形状的认知与描述。

1. 三维形状的认知三维形状是指具有长度、宽度和高度的物体形态。

人们通过视觉感知来获取对于三维形状的认知。

视觉系统能够感知到物体的不同方面，包括形状、大小、位置和方向等。

在认知过程中，大脑会将这些感知信息进行整合和加工，以便我们能够对物体进行识别和理解。

2. 形状描述的方法在三维形状的描述中，我们通常会使用一些几何特征或者词汇来对物体进行描述。

例如，我们可以使用诸如“圆形”、“正方体”、“椭圆形”等词汇来描述物体的基本形状。

此外，我们还可以使用一些几何特征，如长、宽、高等来描述物体的大小和尺寸。

3. 三维形状的识别人们具备将二维图像转化为对应的三维形状的能力。

这个过程需要借助于我们的视觉系统和前期经验。

通过观察物体的棱角、曲线等特征，我们可以将其与我们之前所见过的物体进行比对和匹配，从而进行形状的识别。

因此，前期经验对于三维形状的识别至关重要。

4. 三维形状的描述方法为了更准确地描述三维形状，人们提出了一些专门的数学方法和模型。

例如，我们可以使用CAD软件来对物体进行建模和描述。

CAD软件能够精确地绘制出物体的三维模型，并且可以提供各种几何参数来描述物体的形状和结构。

这些模型可以在工程设计和制造等领域得到广泛应用。

5. 三维形状的应用三维形状的认知和描述在许多领域中起着重要作用。

在建筑设计中，人们需要将设计图纸转化为实际的建筑物，这就需要对其进行三维形状的认知和描述。

在工业制造中，对于产品形状的精确描述有助于生产过程的优化和效率的提高。

此外，在虚拟现实和增强现实技术中，对于三维形状的认知和描述也是实现沉浸式体验的重要基础。

6. 三维形状的发展趋势随着科技的不断发展，三维形状的认知与描述也在不断演进。