内径表示值误差测量结果不确定度分析

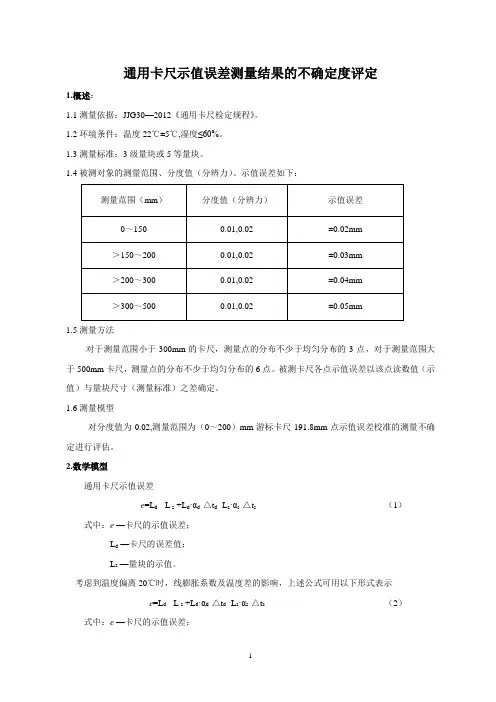
通用卡尺示值误差测量结果的不确定度评定1.概述：1.1测量依据：JJG30—2012《通用卡尺检定规程》。

1.2环境条件：温度22℃±5℃,湿度≤60%。

1.3测量标准：3级量块或5等量块。

1.4被测对象的测量范围、分度值（分辨力）、示值误差如下：1.5测量方法对于测量范围小于300mm的卡尺，测量点的分布不少于均匀分布的3点，对于测量范围大于500mm卡尺，测量点的分布不少于均匀分布的6点。

被测卡尺各点示值误差以该点读数值（示值）与量块尺寸（测量标准）之差确定。

1.6测量模型对分度值为0.02,测量范围为（0～200）mm游标卡尺191.8mm点示值误差校准的测量不确定进行评估。

2.数学模型通用卡尺示值误差e=L d - L s +L d·αd·△t d- L s·αs·△t s （1）式中：e—卡尺的示值误差；L d—卡尺的误差值；L s—量块的示值。

考虑到温度偏离20℃时，线膨胀系数及温度差的影响，上述公式可用以下形式表示e=L d - L s +L d·αd·△t d- L s·αs·△t s （2）式中：e—卡尺的示值误差；L d —卡尺的读数值(20℃条件下)； L s —量块的示值(20℃条件下)；αd 、αs —卡尺和量块的线膨胀系数；△t d 、△t s —卡尺和量块的偏离标准温度20℃的值。

3.方差和灵敏系数由于△t d 和△t s 基本是采用同一支卡尺测量而具有相关性，其数学处理过程比较复杂，为了简化数学处理过程，需要通过如下方法将相关转化为不相关。

令δα=αd -αs δt=△t d -△t s取L≈L d ≈L s α=αd =αs △t =△t d =△t s 得如下示值误差的计算公式：e =L d - L s +L·δα·△t - L·α·δt （3）由公式（3）可以看出，各变量之间彼此不相关，由公式)()(222i ic x u f u ⋅∂∂=χ得： u c2=u 2(e )=c 12·u 12+ c 22·u 22+ c 32·u 32 +c 42·u 42 （4） 式中：11=∂∂=d Le c 12-=∂∂=sL e c t L e c ∆⋅=∂∂=δα3 αδ⋅=∂∂=L tec 4 公式（4） 中u 1,u 2,u 3,u 4分别表示Ld ， L s ，δα，δt 的标准不确定度。

测量结果不确定度及精确度分析刘智敏国际不确定度工作组成员中国计量科学研究院研究员一、术语概念1.真值true value与所给特定量定义一致的值。

2.约定真值conventional true value取作有时是约定作的特定量的值，对所给目的，它有一个合适的不确定度。

3.接受参考值accepted reference value用做比较的同意的参考值。

4.不确定度uncertainty用以表征合理赋予被测量的值的分散性，它是测量结果含有的一个参数。

结果带着的估计值，它表征真值的范围，而真值被认定在其中。

5.精密度precision在规定条件下，独立测得结果间的一致程度。

6.重复性repeatability在重复性条件下，对相同被测量进行接连测量所得结果间的一致程度。

注：重复性条件含：同测量程序、同观测者、同仪器、同地点、短期内重复。

7.再现性reproducibility在改变了的测量条件下，对相同被测量测量结果之间的一致程度。

注：改变条件可含：原理、方法、观测者、仪器、标准、地点、条件、时间，改变条件应列出。

8.正确度，真实度trueness由很大一系列测得结果平均值与接受参考值之间的一致程度。

9.偏倚bias测得结果的期望与接受参考值之差。

正确度测度常用偏倚。

10.精确度，准确度accuracy测量结果与被测量真值间的一致程度。

注：精确度定量表示用不确定度，精确度简称精度。

11.误差error测量结果减被测量真值。

12. 随机误差 random error以不可预知方式变化的误差。

13. 系统误差 systematic error保持不变或按预期规律变化的误差。

14. 概率 probability随机事件带有的一个实数，范围从0到1。

15. 随机变量（ξ）random variable()()x F x P =≤ξ 可定注：离散型：()i i p x P ==ξ连续型：()()dx x f x F x⎰∞−=, ()x f 为分布密度16. 期望 expectation离散型：∑=i i x p E ξ 连续型：()dx x xf E ⎰=ξ17. 方差 variance()2ξξξE E V −=18. 标准差，标准偏差 standard deviationξξσV =19. 变异系数，变化系数（CV , COV ）coefficient of variation对非负号 ξξσE =CV不确定度和精确度示意图二、计算2.1 标准差传播()n x x x f y ,...,,21= ()()()()()j i j i j N i Ni j i i Ni ix x x x x f x f x x fy σσρσσ,21112212∂∂∂∂+⎪⎪⎭⎫⎝⎛∂∂=∑∑∑−=+== 式中相关系数 ()()()()jij i j i xx x x x x σσρ,COV ,=[]1,0∈而协方差 covariance ()()()j j i i j i Ex x Ex x E x x −−=,COV无关时 ()()i i x xfy 222σσ∑⎪⎪⎭⎫ ⎝⎛∂∂= 提高正确度提高精密度例：平均值标准差对某量等精度独立测得n x x x ,.....,21； ()σσ=i x平均值 ∑=i x nx 1()22221n nn x σσσ==()nx i σσ=2.2 不确定度评定以标准差表示的不确定度叫标准不确定度u , 将u 乘以包含因子k 得U ＝ku ，叫展伸不确定度。

指示表的示值误差测量结果的不确定度分析1测量方法依据《JJG34-2008指示表（指针式、数显式）检定规程》、《JJG35-2006杠杆表检定规程》、《JJF1102-2003内径表校准规范》、《JJG379-2009大量程百分表检定规程》、《JJG830-2007深度指示表检定规程》，《JJG109-2004百分表式卡规检定规程》、《JJF1253-2010带表卡规校准规范》、《JJF1255-2010厚度表校准规范》、依据《JJF1059.1-2012测量不确定度评定与表示》要求，指示表示值误差是用相应准确度等级的指示类量具检定仪,按规定的测量间隔在正向进行检定,取正行程中的各受检点误差中最大值与最小值之差作为全量程的示值误差。

2测量模型现对量程为10mm 指示表(分度值为0.01mm)的10mm 点和量程为1mm 的 指示表(分度值或分辨力为0.001mm)1mm 点的示值误差测量结果不确定度进行分析计算。

指示表的示值误差e : =e d L -S L +d d d t L ∆⋅⋅αΔt d -s S S t L ∆⋅⋅αL S (1.1)式中： d L ------指示表的示值（20℃条件下） S L ------检定仪的示值（20℃条件下） αd 、αs ------分别为指示表和检定仪的线胀系数Δt d 、Δt s ------分别为指示表和检定仪偏离温度20℃时的数值令 s d ααδα-=;s d t t t ∆-∆=δ取 s d L L L ≈≈；α≈αd ≈αs ;s d t t t ∆≈∆≈∆ 得 =e d L -S L +t L t L δαδα⋅⋅-⋅∆⋅(1.2)3灵敏系数C 1=∂e/∂L d =1; C 2=∂e/∂L s =1C 3=∂e/∂δα=t L ∆⋅ C 4=∂e/∂δt = α⋅L4不确定度来源 4.1 读数误差：1u4.2 检定仪的误差：2u 4.2.1检定仪的示值误差:1.2u 4.2.2检定仪的对线误差:2.2u 4.3测量重复性 4.4线胀系数误差: 3u4.5指示表和检定仪的温度差: 4u 5 不确定度一览表以分度值为0.01mm 、0.001mm 的指示表为例分别见表C.1和表C.2。

浅论测量仪器的误差和测量不确定度摘要本文从概念、逻辑和形式上对测量仪器的误差和测量不确定度进行了分析与研究，深入浅出的剖析了测量仪器的示值误差、最大允许误差和测量不确定度之间的关系。

旨在引起重视、深入探讨、充分理解、促进共识。

关键词测量仪器；误差；测量不确定度中图分类号p207 文献标识码a 文章编号 1674-6708（2011）44-0058-020 引言在计量检定、校准和检测中，数据处理是一个关键步骤。

在测量过程中，由于测量仪器精度、实验条件局限和各种因素的影响，测量结果总是与实际待测量有一定差异，即存在测量误差。

因此作为一个测量结果，不但应提供测量值的大小和单位，还应对测量值本身的可靠程度作出判断，不说明可靠程度的测量值没有实际意义。

人们在使用误差理论的过程中，又发展出了不确定度概念，如何正确理解、合理表述测量仪器的误差与不确定度，是计量工作者一直关注的重要议题。

1 测量仪器测量仪器的概念是单独地或连同辅助设备一起用以进行测量的器具(又称为计量器具）。

其特点是：1）可直接进行测量；2）可以单独地或连同辅助设备一起使用的一种技术工具或装置。

在我国有关计量法律、法规中，测量仪器称为计量器具，既计量器具是测量仪器的同义语。

测量仪器按其结构特点和计量用途可分为测量用的仪器仪表、实物量具、标准物质及测量系统(或装置)。

测量仪器在生产生活中有着广泛的用途，不论是宇宙飞船探月用的信号发生器，还是平常的买米买菜用的电子称，都是测量仪器。

2 测量仪器的误差测量仪器示值误差，通常简称为测量仪器的误差，可以用绝对误差的形式表示，也可以用相对误差、引用误差的形式表示。

对于给定的测量仪器，由规程、规范所允许的误差极限值，称为测量仪器的最大允许误差，有时也称为测量仪器的允许误差限。

误差是指测量结果减去被测量的真值，误差是测量结果的重要组成部分。

测量结果包括示值、未修正测量结果、已修正测量结果以及若干次测量的平均值。

气动测量仪示值误差测得值的不确定度分析摘要：随着产业4.0的引进和智能制造的不断推进，制造业与互联网产业的融合更加紧密，越来越多的零部件得到了智能测试和数字化；但是，在传统的生产管理中，质量控制方面仍然存在重大缺陷:一方面，大多数企业继续采用人工测量和抽查，这需要时间和努力，并且难以保证测量的准确性；另一方面，数据存储管理缺乏可持续性，缺乏高质量的数据分析和控制，难以及时发现生产问题，容易给企业造成巨大的物质损失。

针对这些实际问题，提出利用气动仪器测量质量参数，建立网络技术数据优化和调节系统，实现生产质量的可视化监控。

近年来，一些专家学者还开展了大量关于气动计量的理论和实践研究，胡小平等人分析了背压道路的特征曲线，研究了主要参数对计量的影响；Cz研究了气动仪器校准的不确定性和线性度。

J.Jermak等人使用不同的线性近似方法来减少非线性；miroslawruck等人在一个尺寸控制系统中研究了气动仪器，并建议使用两个以上的调节主机可以大大提高线性度；许多专家就提高气动仪器测量的准确性发表了意见。

关键词：气动量仪;浮标式;电子柱式;不确定度分析引言从较长远的角度发展了测圆器的理论和方法，工业制造工艺主要依靠科学检测仪器和适当的数据分析方法，以确保产品测圆器控制在最大容许误差内。

近年来，随着检测技术和计算机化技术的改进，舍入测量技术继续得到改进和发展。

其中，数值电子空气动力学测量原理的节拍误差测量方法应用于实际生产过程，发展迅速。

1系统总体架构本系统以齿轮内径为研究对象，主要通过气动仪表的压力差特性获取齿轮加工后内径测量数据，以确保气动仪表测量精度，通过优化设计提高测量精度数据优化和调节系统结合相关框架软件使用Java编程实现了对系统的直接浏览器访问，具有高度的可扩展性，可以快速转换为基于系统的其他零件的相关分析系统；数据流量使用基于以太网卡的TCP/IP自动执行数据传输。

整个系统在齿轮的制造和质量控制方面发挥了重要作用。

内径千分尺示值误差测量结果不确定度评定1 概述1.1测量依据：JJG 22-2014 《内径千分尺检定规程》。

1.2 环境条件：温度一般控制在（20±3）℃以内，每小时变化量不大于0.5℃。

1.3测量标准：3等量块，扩展不确定度为)1011.0(699L m U -⨯+=μ，0.3=k 包含因子：；万能测长仪，示值误差的最大允许值（任意零位）为()L 61055.0-⨯+±。

1.4 被测对象：内径千分尺/（50～600）mm 。

1.5 测量方法：依据本规程，内径千分尺的示值误差的校准是在规程中允许的温度条件下，进行充分等温后，以与标准量块用测长仪进行比较测量得到的。

2 数学模型 s L L L -=∆式中：L —内径千分尺示值;s L —测长仪示值。

3 灵敏系数1/1=∂∆∂=L L c ； 1/2-=∂∆∂=s L L c 。

4 各输入量的不确定度分量的评定4.1输入量L 的标准不确定度)(L u 评定输入量L 的标准不确定度来源主要是测量重复性引入的标准不确定度)(L u ，用A 类标准不确定度评定。

当L =200mm 时，在重复测量条件下，用测长仪连续测量10次，求得单次测量实验标准差m s μ1=,则)(L u =m s μ1=。

当L =500mm 时，在重复测量条件下，用测长仪连续测量10次，求得单次测量实验标准差m s μ2.1=,则)(L u =m s μ2.1=。

4.2 输入量s L 的标准不确定度)(s L u 评定输入量s L 的标准不确定度来源主要是校准量块引入的标准不确定度)(1s L u ，内径千分尺与测长仪线胀系数差引入的标准不确定度)(2s L u ，内径千分尺和测长仪间存在温度差引入的标准不确定度)(3s L u4.2.1校准用3等量块引入的标准不确定度)(1s L u ，用B 类标准不确定度评定。

检定证书给出3等量块的扩展不确定度为)1011.0(699L m U -⨯+=μ，0.3=k 包含因子：，则当L =200mm 时，m u μ10.00.3/3.01==当L =500mm 时，m u μ20.00.3/6.01==4.2.2 内径千分尺与测长仪线胀系数差引入的标准不确定度)(2s L u ，用B 类标准不确定度评定。

内径千分尺示值误差的测量结果不确定度1、概述1.1测量方法: 依据JJG22-2003《内径千分尺》检定规程1.2环境条件: 温度(20±3)℃, 相对湿度≤65%1.3测量标准: 4等2级(83块组)量块，测量范围:(0.5～100)mm1.4测量对象: 分度值0.01mm、测量范围（0～500）mm的内径千分尺1.5测量过程内径千分尺的示值误差用测长仪进行检定，受检点为测量范围内均匀分布的5点。

各点示值误差以该点读数与标准量块尺寸之差来确定。

1.6评定结果的使用符合上述条件下的测量结果，一般可直接使用本不确定度的评定结果2、数学模型e=l m—l b+ l m×a m×△t m—l b×a b×△t b式中：l m和l b—分别是内径千分尺的示值和量块的长度（标准条件下）；a m和a b—分别是内径千分尺和量块的热膨胀系数；△t m和△t b—分别是内径千分尺和量块偏离参考温度20℃的数值。

3、方差和传播系数令：δa = a m—a bδt=△t m—△t b舍弃高阶微分量，取：l≈l m≈l ba≈a m≈a b△t≈△t m≈△t b则：e=l m—l b+ l×△t×δa+l×a×δt得：2c u =)(2e u = 21c ×21u + 22c ×22u + 23c ×23u + 24c ×24u 式中：1c =cl f ∂∂= 1 2c =bl e∂∂= -13c =aeδ∂∂=l ×t ∆ 4c =t e δ∂∂=l ×a1u ，2u ，3u 和4u — 分别为l m ，l b ，δa 和δt 的不确定度。

2c u =)(2e u = 21u + 22u +（l ×△t ）2×23u +（l ×a ）2×24u 4、标准不确定度一览表 4.1 l =50mm 时，如表4-1所示。

桐乡市计量检定测试所技术文件千分尺示值误差测量结果的不确定度评定千分尺示值误差测量结果的不确定度评定过程1 概述1.1 测量方法：依据JJG21-1995《千分尺》国家计量检定规程。

1.2 环境条件：温度（20±5)℃。

1.3 测量标准：五等量块，其长度尺寸的不确定度不大于（0.5+5L）µm(L—校准长度)，包含因子k 取2.7。

1.4 被测对象：校准范围为(0~25)mm，分度值为0.01mm的千分尺，MPE为±4µm。

1.5 测量过程千分尺示值误差是以五等量块进行校准的，千分尺的校准点均匀分布于校准范围5点上。

被测量千分尺各点示值误差以该点读数值（示值）与量块尺寸（测量标准）之差确定。

1.6 评定结果的使用在符合上述条件下的测量结果，一般可直接使用本不确定度的评定结果。

2 数学模型e =L a+L o-L s式中：e ——千分尺某点示值误差；L a——千分尺测微头25mm内示值；L o——对零量块的长度；L s——校准量块的长度。

3 输入量的标准不确定度的评定3.1 输入量L a的标准不确定度u(L a)的评定输入量L a的不确定度来源主要是测量重复性引起的标准不确定度u(L a)的评定，可以通过连续测量得到测量列（采用A类方法进行评定）。

以测微头25mm示值为例，在重复性条件下，用量块连续测量10次，得到测量列25.003mm，25.003mm，25.002mm，25.002mm，25.002mm，25.003mm，25.003mm，25.002mm，25.002mm，25.002mm。

a = 25.0023mm单次标准差s== 0.00048mm ≈ 0.48µm则可得到u(L a)= s=0.48µm自由度v(L a)= 10-1=93.2输入量L0的标准不确定度u(L0)的评定输入量L0的不确定度来源主要是对零量块引起的标准不确定度u(L0)（采用B类方法进行评定）。

精密压力表示值误差的测量结果不确定度评定发布时间：2021-04-27T09:59:53.680Z 来源：《科学与技术》2021年1月3期作者：吴超[导读] 弹簧管式精密压力表使用方便又经济耐用，吴超伊春市检验检测中心黑龙江伊春 153000摘要：弹簧管式精密压力表使用方便又经济耐用，被很多的实验室作为压力测量和标准使用。

本文根据对《测量不确定度评定与表示》的理解，对0.4 级精密压力表示值误差测量结果的不确定度评定进行了分析。

关键词：压力表；测量示值；误差弹簧管式精密压力表是以弹簧管为敏感元件的压力测量仪表。

对具体的测量进行具体的分析，给出更为符合测量环境的测量不确定度评定，是一项极有意义的工作。

通常，在不确定度的评定中，测量者和利益相关各方面最为关心的是测量是否有效，测量结果是否可信，对测量的可信程度提出疑问，回答这些问题有一定的难度，因为影响测量结果的因素很多，而人们对诸多影响因素往往缺乏完整的了解，故引入“测量不确定度”的概念，利用它的表示来评定测量水平或质量，是计量界在误差理论的基础上进行大量研究的一个重要成果，不确定度是对测量结果质量的定量表征，结果的可用性很大程度上取决于其不确定度大小。

测量误差和不确定度是计量学领域里最基本、最重要的理论知识，也是难点之一.一、测量概述（1）环境条件：室温（20±5）℃。

（2）测量标准：二等活塞压力计，不确定度：二等。

（3）依据《弹簧管式精密压力表和真空压力表》JJG49- 1999规程。

（4）被测对象：精密压力表，测量范围（1～60）MPa。

（5）测量原理及其组成：二等活塞式压力计是根据流体静力平衡原理设计制造的。

其工作原理就是基于活塞本身重量和加在活塞上的专用砝码重量，与作用在活塞面积上所产生的压力相平衡。

二、数学模型根据弹簧管式精密压力表和真空压力表的检定方法，可建立如下数学模型式中：δ—被检压力表示值误差；p1—被检压力表示值；p2—标准压力值。