下载文档原格式
将军饮马(作对称点求最短线段终极版)背景知识：早在古罗马时代，传说亚历山大城有一位精通数学和物理的学者，名叫海伦．一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题．将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的军营B开会，应该怎样走才能使路程最短？这个问题的答案并不难，据说海伦略加思索就解决了它．从此以后，这个被称为“将军饮马”的问题便流传至今．常用知识点：两点之间线段最短，垂线段最短，三角形三边关系，轴对称，平移；解题思路：找对称点，变折线为直线。
常见模型：一、两定点一动点型：如图：在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB最小。
解题思路：连接AB，与直线的交点为点Q，即此时点P运动到点Q处，最小值为AB.证明：运用三角形三边关系：两边之和大于第三边，当A、P、B三点共线可取等于。
在定直线l上找一个动点P，使动点P到两个定点A与B的距离之和最小，即PA+PB的和最小.解题思路：作定点B关于直线l的对称点C,连接AC,交直线于点Q，当点P运动到点Q，最小值为AC.证明：关键是作其中一个定点的对称点，使得PB=PC，求PA+PB的最小值，即求PA+PC的最小值。
再转化为上述题型。
PA-值最大。
引申1：此题型也可以求PB解题思路：延长AB交直线l于点Q,当点P运动到点Q，PBPA-最大值为AB.证明：三角形任意两边之差小于第三边，当A、B、P三点共线可取等于.(提示：如果两定点不在直线的同侧，可以作其中一个定点关于直线l的对称点)PA-值最小。
引申2：此题型也可以求PB解题思路：连接AB，作AB的垂直平分线角l于点P.证明：垂直平分线上的点到线段的两端距离相等，可得PA=PB二.两动点一定点型（两动点在角的两边上）如图，在∠MON 的内部有一点A ，在OM 上找一点B ，在ON 上找一点C ，使得△BAC 周长最短．解题思路：作点A 关于OM 的对称点'A ，作点A 关于ON 的对称点''A ，连接'''A A ，与OM 交于点B ， 与ON 交于点C ，连接AB ，AC ，此△ABC 周长最短．证明：两点之间，线段最短变式1：如图：在∠MON 的内部有一点A ，在OM 上找一点B ，在ON 上找一点C ，使得AB ＋BC 最短．解题思路:作点A 关于OM 的对称点'A ，过点'A 作C A '⊥ON ，交OM 于点B ，交ON 于点C,即为所求。
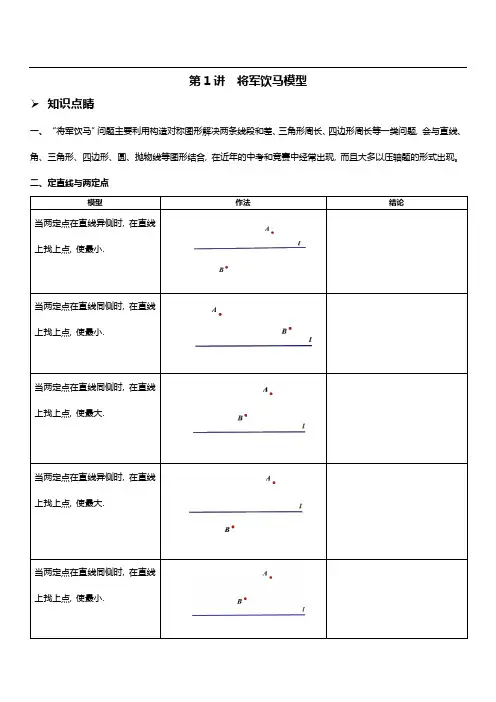
第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。
二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点（在左）, 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A ．例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A （4,4）, 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C ．,D ．第3题图 第4题图 第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5：如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________．A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图 第8题图 第9题图A ．例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA ．例10: 如图, 矩形ABOC 的顶点A 的坐标为（-4,5）, D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图 第11题图 第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图 第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N （3,0）是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15：如图, 已知正比例函数y=kx （k>0）的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为（0, 4）, P 为y 轴上的一个动点, M 、N 为函数y=kx （k>0）的图像上的两个动点, 则AM+MP+PN 的最小值为___________．第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为（6, 4）, E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17：如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值．x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。
2020中考数学复习微专题：最值问题（将军饮马）突破与提升策略【问题引入】“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。
【问题描述】如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？A B将军军营河【问题简化】如图，在直线上找一点P使得P A+PB最小？P【问题分析】这个问题的难点在于P A+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．【问题解决】作点A关于直线的对称点A’，连接P A’，则P A’=P A，所以P A+PB=P A’+PB当A’、P、B三点共线的时候，P A’+PB=A’B，此时为最小值（两点之间线段最短）【思路概述】作端点（点A或点B）关于折点（上图P点）所在直线的对称，化折线段为直线段．将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N，使得△PMN周长最小．B B此处M、N均为折点，分别作点P关于OA（折点M所在直线）、OB（折点N所在直线）的对称点，化折线段PM+MN+NP为P’M+MN+NP’’，当P’、M、N、P’’共线时，△PMN周长最小．【例题】如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为___________．P O B AMN【分析】△PMN周长即PM+PN+MN的最小值，此处M、N均为折点，分别作点P关于OB、OA对称点P’、P’’，化PM+PN+MN为P’N+MN+P’’M．P''A当P’、N、M、P’’共线时，得△PMN周长的最小值，即线段P’P’’长，连接OP’、OP’’，可得△OP’P’’为等边三角形，所以P’P’’=OP’=OP=8．A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
专题几何最值之将军饮马问题【热点专题】“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题，会与直线、角、三角形、四边形、圆、抛物线等图形结合，在近年的中考和竞赛中经常出现，而且大多以压轴题的形式出现.【抽象模型】如图，在直线上找一点P使得PA+PB最小？【模型解析】作点A关于直线的对称点A’，连接PA’，则PA’=PA，所以PA+PB=PA’+PB当A’、P、B三点共线的时候，PA’+PB=A’B，此时为最小值（两点之间线段最短）题型一：两定一动模型当两定点【例1】1．如图，点C的坐标为（3，y），当△ABC的周长最短时，求y的值.【例2】2．如图，正方形ABCD中，AB=7，M是DC上的一点，且DM=3，N是AC上的一动点，求|DN-MN|的最小值与最大值．【例3】3．如图1（注：与图2完全相同），在直角坐标系中，抛物线经过点三点A(1，0),B(5，0),C(0，4)．（1）求抛物线的解析式和对称轴；（2）P是抛物线对称轴上的一点，求满足PA+PC的值为最小的点P坐标（请在图1中探索）；（3）在第四象限的抛物线上是否存在点E，使四边形OEBF是以OB为对角线且面积为12的平行四边形？若存在，请求出点E坐标，若不存在请说明理由.（请在图2中探索）题型二：一定两动模型模型作法结论点P 在∠AOB 内部，在OB 边上找点D ，OA 边上找点C ，使得△PCD 周长最小.分别作点P 关于OA 、OB 的对称点P ′、P ″，连接P ′P ″，交OA 、OB 于点C 、D ，点C 、D 即为所求.△PCD 周长的最小值为P ′P ″点P在∠AOB 内部，在OB 边上找点D ，OA 边上找点C ，使得PD ＋CD 最小.作点P 关于OB 的对称点P ′，过P ′作P ′C ⊥OA 交OB 于D ，点C 、点D 即为所求.PD ＋CD 的最小值为P ′C【例4】4．如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为___________.【例5】5．如图，点P 是∠AOB 内任意一点，且∠AOB ＝40°，点M 和点N 分别是射线OA 和射线OB 上的动点，当△PMN周长取最小值时，则∠MPN的度数为（）A．140°B．100°C．50°D．40°【例6】6．如图，在正方形ABCD中，点E，F分别是边AD，BC的中点，连接DF，过点E作EH⊥DF，垂足为H，EH的延长线交DC于点G．（1）猜想DG与CF的数量关系，并证明你的结论；（2）过点H作MN∥CD，分别交AD，BC于点M，N，若正方形ABCD的边长为10，点P是MN上一点，求△PDC周长的最小值．【例7】7．如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x 轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．（1）求抛物线的解析式及点D的坐标；（2）当△CMN是直角三角形时，求点M的坐标；（3）试求出AM+AN的最小值．题型三：两定两动模型模型作法结论点P、Q在∠AOB内部，在OB边上找点D，OA边上找点C，使得四边形PQDC周长最小.分别作点P、Q关于OA、OB的对称点P′、Q′，连接P′Q′，分别交OA、OB于点C、D，点C、D即为所求.PC＋CD＋DQ的最小值为P′Q′，所以四边形PQDC周长的最小值为PQ＋P′Q′【例8】8．如图，在矩形ABCD 中，AB =4，BC =7，E 为CD 的中点，若P 、Q 为BC 边上的两个动点，且PQ =2，若想使得四边形APQE 的周长最小，则BP 的长度应为__________.【例9】9．如图，已知直线l 1∥l 2，l 1、l 2之间的距离为8，点P 到直线l 1的距离为6，点Q 到直线l 2的距离为4，PQ =430，在直线l 1上有一动点A ，直线l 2上有一动点B ，满足AB ⊥l 2，且PA +AB +BQ 最小，此时PA +BQ =______．题型四：两定点一定长模型作法结论如图，在直线l 上找M 、N 两点（M 在左），使得AM ＋MN＋NB 最小，且MN =d .将A 向右平移d 个单位到A ′，作A ′关于l 的对称点A "，连接A "B 与直线l 交于点N ，将点N 向左平移d 个单位即为M ，点M ，N 即为所求.AM ＋MN ＋NB 的最小值为A "B ＋d如图，l 1//l 2，l 1、l 2间距离为d ，在l 1、l 2分别找M 、N 两点，将A 向下平移d 个单位到A ，连接A ′B 交直线l 2于点N ，过点N 作MN ⊥l 1，连接AM .点M 、N 即为所求.AM ＋MN ＋NB 的最小值为A 'B ＋d .使得MN⊥l1，且AM＋MN＋NB最小.【例10】10．在平面直角坐标系中，矩形OABC如图所示，点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=2，当四边形BDEF的周长最小时，求点E的坐标【例11】11．村庄A和村庄B位于一条小河的两侧，若河岸彼此平行，要架设一座与河岸垂直的桥，桥址应如何选择，才使A与B之间的距离最短？12．如图，在Rt△ABC中，∠ACB=90°，AC=6，AB=12，AD平分∠CAB，点F是AC的中点，点E是AD 上的动点，则CE+EF的最小值为（）A．3B．4C．33D．2313．如图，在锐角三角形ABC中，BC=4，∠ABC=60°，BD平分∠ABC，交AC于点D，M、N分别是BD，BC 上的动点，则CM+MN的最小值是（）A．3B．2C．23D．414．如图，在正方形ABCD中，AB=9，点E在CD边上，且DE=2CE，点P是对角线AC上的一个动点，则PE+PD 的最小值是（）A．310B．103C．9D．9215．如图，在正方形ABCD中，E是AB上一点，BE＝2，AB＝8，P是AC上一动点，则PB+PE的最小值_____．16．如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（3，0）是OB上的一定点，点M 是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为______．17．如图，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE=2，当EF＋CF取得最小值时，则∠ECF的度数为多少？18．在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，A（3，0），B（0，4），D为边OB的中点.(1)若E为边OA上的一个动点，求△CDE的周长最小值；(2)若E、F为边OA上的两个动点，且EF=1，当四边形CDEF的周长最小时，求点E、F的坐标.19．如图所示抛物线y=ax2+bx+c过点A−1,0，点C0,3，且OB=OC（1）求抛物线的解析式及其对称轴；（2）点D,E在直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值；（3）点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3∶5两部分，求点P的坐标.20．如图，在平面直角坐标系中，矩形OABC的边BC交x轴于点D，AD⊥x轴，反比例函数y=k(x>0)的图x象经过点A，点D的坐标为(3,0)，AB=BD．（1）求反比例函数的解析式；（2）点P为y轴上一动点，当PA+PB的值最小时，求出点P的坐标．21．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．。
最值系列之——将军饮马一、什么是将军饮马？【问题引入】“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。
【问题描述】如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？A B军军军军军【问题简化】如图，在直线上找一点P使得PA+PB最小？【问题分析】这个问题的难点在于PA+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．【问题解决】作点A关于直线的对称点A’，连接PA’，则PA’=PA，所以PA+PB=PA’+PB当A’、P、B三点共线的时候，PA’+PB=A’B，此时为最小值（两点之间线段最短）【思路概述】作端点（点A或点B）关于折点（上图P点）所在直线的对称，化折线段为直线段．二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N，使得△PMN周长最小．B B此处M、N均为折点，分别作点P关于OA（折点M所在直线）、OB（折点N所在直线）的对称点，化折线段PM+MN+NP为P’M+MN+NP’’，当P’、M、N、P’’共线时，△PMN周长最小．【例题】如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为___________．P O B AN【分析】△PMN周长即PM+PN+MN的最小值，此处M、N均为折点，分别作点P关于OB、OA对称点P’、P’’，化PM+PN+MN为P’N+MN+P’’M．当P’、N、M、P’’共线时，得△PMN周长的最小值，即线段P’P’’长，连接OP’、OP’’，可得△OP’P’’为等边三角形，所以P’P’’=OP’=OP=8．【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
最值系列之——将军饮马一、什么是将军饮马？【问题引入】“白日登山望烽火，黄昏饮马傍交河”，这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题，通常称为“将军饮马”。
【问题描述】如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？A B将军军营河【问题简化】如图，在直线上找一点P使得P A+PB最小？【问题分析】这个问题的难点在于PA+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．【问题解决】作点A关于直线的对称点A’，连接P A’，则P A’=P A，所以P A+PB=P A’+PB当A’、P、B三点共线的时候，P A’+PB=A’B，此时为最小值（两点之间线段最短）【思路概述】作端点（点A或点B）关于折点（上图P点）所在直线的对称，化折线段为直线段．二、将军饮马模型系列【一定两动之点点】在OA、OB上分别取点M、N，使得△PMN周长最小．B B此处M、N均为折点，分别作点P关于OA（折点M所在直线）、OB（折点N所在直线）的对称点，化折线段PM+MN+NP为P’M+MN+NP’’，当P’、M、N、P’’共线时，△PMN周长最小．【例题】如图，点P是∠AOB内任意一点，∠AOB=30°，OP=8，点M和点N分别是射线OA和射线OB上的动点，则△PMN周长的最小值为___________．P O B AMN【分析】△PMN周长即PM+PN+MN的最小值，此处M、N均为折点，分别作点P关于OB、OA对称点P’、P’’，化PM+PN+MN为P’N+MN+P’’M．P''A当P’、N、M、P’’共线时，得△PMN周长的最小值，即线段P’P’’长，连接OP’、OP’’，可得△OP’P’’为等边三角形，所以P’P’’=OP’=OP=8．A【两定两动之点点】在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
