必修五数列综合复习——高一数学讲义

高一数学数列知识总结知识网络二、知识梳理一、看数列是不是等差数列有以下三种方法： ①),2(1为常数d n d a a n n ≥=-- ②211-++=n n n a a a (2≥n ) ③b kn a n +=(k n ,为常数).二、看数列是不是等比数列有以下两种方法： ①)0,,2(1≠≥=-且为常数q n q a a n n②112-+⋅=n n na a a (2≥n ，011≠-+n n n a a a )三、在等差数列｛n a ｝中,有关S n 的最值问题：(1)当1a >0,d<0时，满足⎩⎨⎧≤≥+001m m a a 的项数m 使得m s 取最大值. (2)当1a <0,d>0时，满足⎩⎨⎧≥≤+001m m a a 的项数m 使得m s 取最小值。

在解含绝对值的数列最值问题时,注意转化思想的应用。

四.数列通项的常用方法：（1）利用观察法求数列的通项.（2）利用公式法求数列的通项：①⎩⎨⎧≥-==-)2()111n S S n S a n n n（；②{}n a 等差、等比数列{}n a 公式.（3）应用迭加（迭乘、迭代）法求数列的通项：①)(1n f a a n n +=+；②).(1n f a a n n =+（4）造等差、等比数列求通项：① q pa a n n +=+1；②nn n q pa a +=+1；③)(1n f pa a n n +=+；④n n n a q a p a ⋅+⋅=++12.第一节通项公式常用方法题型1 利用公式法求通项例1：1.已知{a n }满足a n+1=a n +2，而且a 1=1。

求a n 。

2.已知n S 为数列{}n a 的前n 项和，求下列数列{}n a 的通项公式：⑴ 1322-+=n n S n ； ⑵12+=nn S .总结:任何一个数列，它的前n 项和n S 与通项n a 都存在关系：⎩⎨⎧≥-==-)2()1(11n S S n S a n n n 若1a 适合n a ，则把它们统一起来，否则就用分段函数表示. 题型2 应用迭加（迭乘、迭代）法求通项例2：⑴已知数列{}n a 中，)2(12,211≥-+==-n n a a a n n ，求数列{}n a 的通项公式；⑵已知n S 为数列{}n a 的前n 项和，11=a ，n n a n S ⋅=2，求数列{}n a 的通项公式.总结：⑴迭加法适用于求递推关系形如“)(1n f a a n n +=+”； 迭乘法适用于求递推关系形如“)(1n f a a n n ⋅=+“；⑵迭加法、迭乘法公式：① 11232211)()()()(a a a a a a a a a a n n n n n n n +-++-+-+-=----- ② 1122332211a a aa a a a a a a a a n n n n n n n ⋅⋅⋅⋅⋅⋅=----- . 题型3 构造等比数列求通项例3已知数列{}n a 中，32,111+==+n n a a a ，求数列{}n a 的通项公式.总结：递推关系形如“q pa a n n +=+1” 适用于待定系数法或特征根法：①令)(1λλ-=-+n n a p a ；② 在q pa a n n +=+1中令pqx x a a n n -=⇒==+11，∴)(1x a p x a n n -=-+； ③由q pa a n n +=+1得q pa a n n +=-1，∴)(11-+-=-n n n n a a p a a .例4已知数列{}n a 中，nn n a a a 32,111+==+，求数列{}n a 的通项公式.总结：递推关系形如“nn n q pa a +=+1”通过适当变形可转化为： “q pa a n n +=+1”或“nn n n f a a )(1+=+求解.例5已知数列{}n a 中，n n n a a a a a 23,2,11221-===++，求数列{}n a 的通项公式.总结：递推关系形如“n n n a q a p a ⋅+⋅=++12”，通过适当变形转化为可求和的数列. 强化巩固练习1、已知n S 为数列{}n a 的前n 项和， )2,(23≥∈+=+n N n a S n n ，求数列{}n a 的通项公式.2、已知数列{}n a 中，)(0)1()2(,211++∈=+-+=N n a n a n a n n ，求数列{}n a 的通项公式. 小结：数列通项的常用方法：⑴利用观察法求数列的通项；⑵利用公式法求数列的通项；⑶应用迭加（迭乘、迭代）法求数列的通项：①)(1n f a a n n +=+；②).(1n f a a n n =+（4）构造等差、等比数列求通项：①q pa a n n +=+1；②n n n q pa a +=+1；③)(1n f pa a n n +=+；④n n n a q a p a ⋅+⋅=++12.3、数列{}n a 中，)(,111n n n a a n a a -==+，则数列{}n a 的通项=n a 。

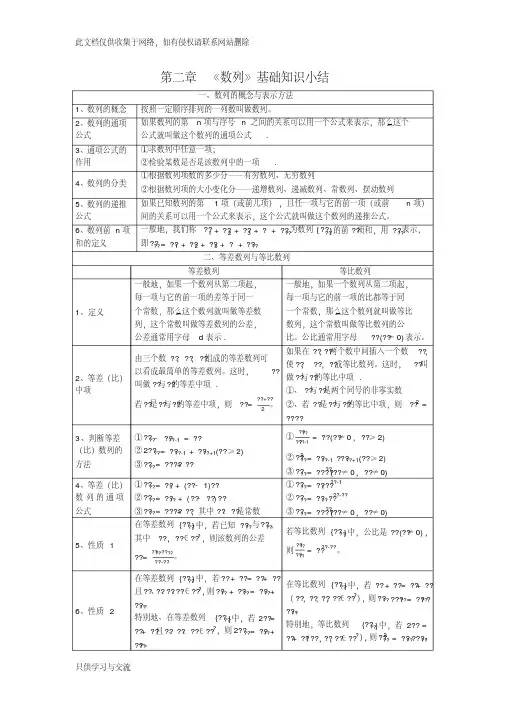
第二章：数列一、数列的概念1、数列的概念：一般地，按一定次序排列成一列数叫做数列，数列中的每一个数叫做这个数列的项，数列的一般形式可以写成a a a a n ,,,,,123，简记为数列a n {}，其中第一项a 1也成为首项；a n 是数列的第n 项，也叫做数列的通项.数列可看作是定义域为正整数集*N （或它的子集）的函数，当自变量从小到大取值时，该函数对应的一列函数值就是这个数列.2、数列的分类：按数列中项的多数分为：（1） 有穷数列：数列中的项为有限个，即项数有限； （2） 无穷数列：数列中的项为无限个，即项数无限.3、通项公式：如果数列a n {}的第n 项a n 与项数n 之间的函数关系可以用一个式子表示成=a f n n ()，那么这个式子就叫做这个数列的通项公式，数列的通项公式就是相应函数的解析式.4、数列的函数特征：一般地，一个数列a n {}，如果从第二项起，每一项都大于它前面的一项，即>+a a n n 1，那么这个数列叫做递增数列;高一数学必修5：数列（知识点梳理）如果从第二项起，每一项都小于它前面的一项，即1n n a a +<，那么这个数列叫做递减数列; 如果数列的各项都相等，那么这个数列叫做常数列.5、递推公式：某些数列相邻的两项（或几项）有关系，这个关系用一个公式来表示，叫做递推公式．二、等差数列1、等差数列的概念：如果一个数列从第二项起，每一项与前一项的差是同一个常数，那么这个数列久叫做等差数列，这个常数叫做等差数列的公差.即1n n a a d +-=（常数），这也是证明或判断一个数列是否为等差数列的依据.2、等差数列的通项公式：设等差数列的首项为1a ，公差为d ，则通项公式为：()()()11,n m a a n d a n m d n m N +=+-=+-∈、.3、等差中项：（1）若a A b 、、成等差数列，则A 叫做a 与b 的等差中项，且=2a bA +; （2）若数列为等差数列，则12,,n n n a a a ++成等差数列，即1n a +是与2n a +的等差中项，且21=2n n n a a a +++；反之若数列满足21=2n n n a a a +++，则数列是等差数列.4、等差数列的性质：（1）等差数列中，若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a +=+，若2m n p +=，则2m n p a a a +=；（2）若数列和{}n b 均为等差数列，则数列{}n n a b ±也为等差数列；（3）等差数列{}n a 的公差为d ，则{}0n d a >⇔为递增数列，{}0n d a <⇔为递减数列，{}0n d a =⇔为常数列.5、等差数列的前n 项和n S ：（1）数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈；（2）数列{}n a 的通项与前n 项和n S 的关系：11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩（3）设等差数列{}n a 的首项为1,a 公差为d ，则前n 项和()()111=.22n n n a a n n S na d +-=+6、等差数列前n 和的性质：（1）等差数列{}n a 中，连续m 项的和仍组成等差数列，即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等差数列（即232,,,m m m m m S S S S S --成等差数列）；（2）等差数列{}n a 的前n 项和()2111==,222n n n d d S na d n a n -⎛⎫++- ⎪⎝⎭当0d ≠时，n S 可看作关于n 的二次函数，且不含常数项；（3）若等差数列{}n a 共有2n+1（奇数）项，则()11==,n S n S S a S n++-奇奇偶偶中间项且若等差数列{}n a 共有2n （偶数）项，则1==.n nS a S S nd S a +-偶奇偶奇且7、等差数列前n 项和n S 的最值问题：设等差数列{}n a 的首项为1,a 公差为d ，则（1）100a d ><且（即首正递减）时，n S 有最大值且n S 的最大值为所有非负数项之和； （2）100a d <>且（即首负递增）时，n S 有最小值且n S 的最小值为所有非正数项之和.三、等比数列1、等比数列的概念：如果一个数列从第二项起，每一项与前一项的比是同一个不为零的常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母q 表示（0q ≠）.即()1n na q q a +=为非零常数，这也是证明或判断一个数列是否为等比数列的依据.2、等比数列的通项公式：设等比数列{}n a 的首项为1a ，公比为q ，则通项公式为：()11,,n n m n m a a qa q n m n m N --+==≥∈、.3、等比中项：（1）若a A b 、、成等比数列，则A 叫做a 与b 的等比中项，且2=A ab ; （2）若数列{}n a 为等比数列，则12,,n n n a a a ++成等比数列，即1n a +是与2n a +的等比中项，且212=n n n a a a ++⋅；反之若数列{}n a 满足212=n n n a a a ++⋅，则数列{}n a 是等比数列.4、等比数列的性质：（1）等比数列{}n a 中，若(),m n p q m n p q N ++=+∈、、、则m n p q a a a a ⋅=⋅，若2m n p +=，则2m n p a a a ⋅=；（2）若数列{}n a 和{}n b 均为等比数列，则数列{}n n a b ⋅也为等比数列；（3）等比数列{}n a 的首项为1a ，公比为q ，则{}1100101na a a q q ><⎧⎧⇔⎨⎨><<⎩⎩或为递增数列，{}1100011n a a a q q ><⎧⎧⇔⎨⎨<<>⎩⎩或为递减数列， {}1n q a =⇔为常数列.5、等比数列的前n 项和：（1）数列{}n a 的前n 项和n S =()1231,n n a a a a a n N -++++++∈；（2）数列{}n a 的通项与前n 项和n S 的关系：11,1.,2n n n S n a S S n -=⎧=⎨-≥⎩ （3）设等比数列{}n a 的首项为1a ，公比为()0q q ≠，则()11,1.1,11n n na q S a q q q=⎧⎪=-⎨≠⎪-⎩由等比数列的通项公式及前n 项和公式可知，已知1,,,,n n a q n a S 中任意三个，便可建立方程组求出另外两个.6、等比数列的前n 项和性质：设等比数列{}n a 中，首项为1a ，公比为()0q q ≠，则 （1）连续m 项的和仍组成等比数列，即12122,,m m m m a a a a a a ++++++++21223m m m a a a +++++,仍为等比数列（即232,,,m m m m m S S S S S --成等差数列）；（2）当1q ≠时，()()11111111111111n n n n n a q a a a a aS q q q qq q q q q -==⋅-=-⋅=⋅-------， 设11a t q =-，则n n S tq t =-.四、递推数列求通项的方法总结1、递推数列的概念：一般地，把数列的若干连续项之间的关系叫做递推关系，把表达递推关系的式子叫做递推公式，而把由递推公式和初始条件给出的数列叫做递推数列.2、两个恒等式：对于任意的数列{}n a 恒有：（1）()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-（2）()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈3、递推数列的类型以及求通项方法总结： 类型一（公式法）：已知n S （即12()n a a a f n +++=）求n a ，用作差法：{11,(1),(2)n n n S n a S S n -==-≥类型二（累加法）：已知：数列的首项,且()()1,n n a a f n n N ++-=∈，求n a 通项.给递推公式()()1,n n a a f n n N ++-=∈中的n 依次取1,2,3，……，n-1,可得到下面n-1个式子：()()()()21324311,2,3,,1.n n a a f a a f a a f a a f n --=-=-=-=-利用公式()()()()12132431n n n a a a a a a a a a a -=+-+-+-++-可得：()()()()11231.n a a f f f f n =+++++-类型三（累乘法）：已知：数列的首项,且()()1,n na f n n N a ++=∈，求n a 通项. 给递推公式()()1,n na f n n N a ++=∈中的n 一次取1,2,3，……，n-1,可得到下面n-1个式子： ()()()()23412311,2,3,,1.nn a a aa f f f f n a a a a -====- 利用公式()23411231,0,nn n n a a a a a a a n N a a a a +-=⨯⨯⨯⨯⨯≠∈可得： ()()()()11231.n a a f f f f n =⨯⨯⨯⨯⨯-类型四（构造法）：形如q pa a n n +=+1、n n n q pa a +=+1（q p b k ,,,为常数）的递推数列都可以用待定系数法转化为公比为k 的等比数列后，再求n a 。

高中数学必修5数列的综合复习（详解）【本讲要紧内容】数列基础知识数列的概念、数列的通项公式、数列的递推公式、数列通项公式与前n 项和公式的关系。

【知识把握】 【知识点精析】1. 数列知识有着广泛的应用，而且学习数列对培养和提高观看、分析、归纳等能力都有重要的作用。

2. 数列基础知识〔1〕数列 按一定次序排列的一列数叫做数列，数列中的每一个数都叫做那个数列的项，各项依次叫做那个数列的第1项〔或首项〕，第2项，…，第n 项，…。

例如1，4，7，10，13；1，2，3，4，…，n ，…差不多上数列，数列的一样形式能够写为⋯⋯,,,321n a a a a ，，其中n a 是数列的第n 项，我们常常把上面的数列简记作{}n a 。

项数有限的数列叫做有穷数列，如上面例子中的第1个数列；项数无限的数列叫做无穷数列，如上面例子中的第2个数列，另外，我们依照数列各项数值大小的变化，能够分成递增数列，递减数列，摆动数列和常数数列。

对数列要从函数的高度深刻明白得，数列是定义域为正整数集或它的有限子集上的函数值列。

〔2〕数列的通项公式 假如一个数列的第n 项n a 与项数n 之间的函数关系能够用一个公式来表示，那么那个公式叫做那个数列的通项公式。

例如，数列，，，，65544332…的通项公式能够为*)(21N n n n a n ∈++=；数列2，5，10，17，…的通项公式能够为*)(12N n n a n ∈+=。

一个数列的通项公式的表达式也不一定是唯独的，例如-1，1，-1，1，…的通项公式既能够表示为*)()1(N n a n n ∈-=也能够表示成)(cos *∈=N n n a n π，还能够表示成⎩⎨⎧-=为偶数时为奇数时n ,1n ,1a n〔3〕数列的递推公式 假如数列{}n a 的第1项〔或前n 项〕，且任一项n a 与它的前一项1-n a 〔或前n 项〕间的关系能够用一个公式来表示，那么那个公式就叫做那个数列的递推公式，递推公式也是给出数列的一种方法。

高一数学必修5《数列》复习提纲定鼎教育1. 数列的通项求数列通项公式的常用方法:(1) 观察与归纳法：先观察哪些因素随项数n的变化而变化，哪些因素不变：分析符号、数字、字母与项数n在变化过程中的联系，初步归纳公式。

(2) 公式法：等差数列与等比数列。

(4)构造新数列法；(5)逐项作差求和法；(6)逐项作商求积法2. 等差数列｛a n｝中: (1 )等差数列公差的取值与等差数列的单调性;(2) a n a1 (n 1)d a m (n m)d ；(3) ｛ka n｝也成等差数列;(4)两等差数列对应项和(差)组成的新数列仍成等差数列(8) “首正”的递减等差数列中，前n项和的最大值是所有非负项之和；a b(9) 等差中项：若a, A,b成等差数列，则A ------------ 叫做a b的等差中项。

2(10) 判定数列是否是等差数列的主要方法有：定义法、中项法、通项法、和式法、图像法。

3. 等比数列｛a n｝中:(1) 等比数列的符号特征(全正或全负或一正一负)，等比数列的首项、公比与等比数列的单调性n 1 n m(2) a n ag a m q ；（3）｛|a n|｝、｛ka n｝成等比数列；｛a n｝、｛b n｝成等比数列｛a n b n｝成等比数列（4）两等比数列对应项积（商）组成的新数列仍成等比数列•(5) ai a? La m , a k a k 1L ak m1,L成等比数列《数列》复习(3)利用S n与a n的关系求a n : B n S i，(n 1) & S n 1,(n2),L am, a m 1a m 1L a2m, a2m 1n(q a n)n(n 1) c 2S n2d，S nS2n 1A n f (n)a n f(2 n 1). 2n 1B n b nn p q，i则a ma n a p a q ；若m q, a q p(p q)a p q0，q,S q p(p q)S p q(p q)；-a2m 1 L a3m L仍成等差数列.a ma p a q2S m n S m & mnd .(6)S na PS pna j(q 1)na 1(q 1)(6) S.a 1 a n q ai (1 q n ) (q 1)1a 〔 nq埜(q 1).1 q 1 qq 1 q(7) Pq m n b pb qb n；2m P q b m 2 b p b q S n nS mqS n S nqS（8） “首大于1”的正值递减等比数列中，前 n 项积的最大值是所有大于或等于 1的项的积；“首小于1”的正值递增等比数列中，前 n 项积的最小值是所有小于或等于1的项的积；（9） 并非任何两数总有等比中项 .仅当实数a,b 同号时，实数a,b 存在等比中项.对同号两实数a,b 的等 比中项不仅存在，而且有一对 G ..ab.也就是说，两实数要么没有等比中项 （非同号时），如果有，必有 一对（同号时）。

n n n 一、知识纲要(1)数列的概念，通项公式，数列的分类，从函数的观点看数列． (2)等差、等比数列的定义． (3)等差、等比数列的通项公式． (4)等差中项、等比中项．(5)等差、等比数列的前 n 项和公式及其推导方法． 二、方法总结1. 数列是特殊的函数，有些题目可结合函数知识去解决，体现了函数思想、数形结合的思想．2. 等差、等比数列中， a 1 、 a n 、 n 、 d (q ) 、 S n“知三求二”，体现了方程(组)的思想、整体思想，有时用到换元法． 3. 求等比数列的前 n 项和时要考虑公比是否等于 1，公比是字母时要进行讨论，体现了分类讨论的思想． 4. 数列求和的基本方法有：公式法，倒序相加法，错位相减法，拆项法，裂项法，累加法，等价转化等．三、知识内容： 1. 数列⎧a 1 = S 1(n = 1)数列的通项公式： a n = ⎨ ⎩n - Sn -1 (n ≥ 2) 数列的前 n 项和： S n = a 1 + a 2 + a 3 + + a n1、数列：按照一定顺序排列着的一列数．2、数列的项：数列中的每一个数．3、有穷数列：项数有限的数列．4、无穷数列：项数无限的数列．5、递增数列：从第 2 项起，每一项都不小于它的前一项的数列．6、递减数列：从第 2 项起，每一项都不大于它的前一项的数列．7、常数列：各项相等的数列．8、摆动数列：从第 2 项起，有些项大于它的前一项，有些项小于它的前一项的数列． 9、数列的通项公式：表示数列{a n } 的第 n 项与序号 n 之间的关系的公式．10、数列的递推公式：表示任一项 a n 与它的前一项 a n -1 （或前几项）间的关系的公式．例 1.已知数列{a }的前 n 项和为 S = 2n 2 - n ,求数列{a }的通项公式.当 n = 1时， a 1 = S 1 = 1,当 n ≥ 2 时， a n = 2n 2 - n - 2(n - 1)2 + (n - 1) = 4n - 3 ,经检验 n = 1时 a 1 = 1 也适合 a n = 4n - 3 ,∴ a n = 4n - 3 (n ∈ N + )2. 等差数列等差数列的定义：如果一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母 d 表示。

高一数学必修五数列知识点数列是以正整数集(或它的有限子集)为定义域的函数，是高一学生学习的重点，有哪些知识点要学习呢?下面是店铺给大家带来的高一数学必修五数列知识点，希望对你有帮助。

高一数学必修五数列知识点1.数列的函数理解：①数列是一种特殊的函数。

其特殊性主要表现在其定义域和值域上。

数列可以看作一个定义域为正整数集N*或其有限子集{1，2，3，…，n}的函数，其中的{1，2，3，…，n}不能省略。

②用函数的观点认识数列是重要的思想方法，一般情况下函数有三种表示方法，数列也不例外，通常也有三种表示方法：a.列表法;b。

图像法;c.解析法。

其中解析法包括以通项公式给出数列和以递推公式给出数列。

③函数不一定有解析式，同样数列也并非都有通项公式。

2.通项公式：数列的第N项an与项的序数n之间的关系可以用一个公式an=f(n)来表示，这个公式就叫做这个数列的通项公式(注：通项公式不唯一)。

数列通项公式的特点：(1)有些数列的通项公式可以有不同形式，即不唯一。

(2)有些数列没有通项公式(如：素数由小到大排成一列2，3，5，7，11，...)。

3.递推公式：如果数列{an}的第n项与它前一项或几项的关系可以用一个式子来表示，那么这个公式叫做这个数列的递推公式。

数列递推公式特点：(1)有些数列的递推公式可以有不同形式，即不唯一。

(2)有些数列没有递推公式。

有递推公式不一定有通项公式。

注：数列中的项必须是数，它可以是实数，也可以是复数。

高一数学必修五数列练习1、 ABC的三边a，b，c既成等比数列又成等差数列，则三角形的形状是( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等边三角形2、在等比数列{an}中，a6+a5=a7-a5=48，则S10等于( )A.1023B.1024C.511D.5123、三个数成等比数列，其积为1728，其和为38，则此三数为( )A.3，12，48B.4，16，27C.8，12，18D.4，12，364、一个三角形的三内角既成等差数列，又成等比数列，则三内角的公差等于( )A.0︒B.15︒C.30︒D.60︒5、等差数列{an}中，a1，a2，a4恰好成等比数列，则a1的值是( ) a4A.1B.2C.3D.46、某种电讯产品自投放市场以来，经过三年降价，单价由原来的174元降到58元，这种电讯产品平均每次降价的百分率大约是( )A.29%B.30%C.31%D.32%7、若log4(x+2y)+log4(x-2y)=1，则∣x∣-∣y∣的最小值是。

等差（比）数列的基本运算【例１】n１４（１）求数列{a n}的通项公式；（２）若a３，a５分别为等差数列{b n}的第３项和第５项，试求数列{b n}的通项公式及前n项和S n. [解] （１）设{a n}的公比为q，由已知得１6＝２q３，解得q＝２，∴a n＝２×２n—１＝２n.（２）由（１）得a３＝8，a５＝３２，则b３＝8，b５＝３２．设{b n}的公差为d，则有错误!解得错误!所以b n＝—１6＋１２（n—１）＝１２n—２8．所以数列{b n}的前n项和S n＝错误!＝6n２—２２n.在等差数列和等比数列的通项公式a n与前n项和公式S n中，共涉及五个量：a１，a n，n，d或q，S n，其中a１和d或q为基本量，“知三求二”是指将已知条件转换成关于a１，d q，a n，S n，n 的方程组，利用方程的思想求出需要的量，当然在求解中若能运用等差比数列的性质会更好，这样可以化繁为简，减少运算量，同时还要注意整体代入思想方法的运用.１．已知等差数列{a n}的公差d＝１，前n项和为S n.（１）若１，a１，a３成等比数列，求a１；（２）若S５>a１a9，求a１的取值范围．[解] （１）因为数列{a n}的公差d＝１，且１，a１，a３成等比数列，所以a错误!＝１×（a１＋２），即a错误!—a１—２＝0，解得a１＝—１或a１＝２．（２）因为数列{a n}的公差d＝１，且S５>a１a9，所以５a１＋１0>a错误!＋8a１，即a错误!＋３a１—１0<0，解得—５<a１<２．求数列的通项公式【例２】n n n n（２）数列{a n}的前n项和为S n且a１＝１，a n＋１＝错误!S n，求a n.思路探究：（１）已知S n求a n时，应分n＝１与n≥２讨论；（２）在已知式中既有S n又有a n时，应转化为S n或a n形式求解．[解] （１）当n≥２时，a n＝S n—S n—１＝３＋２n—（３＋２n—１）＝２n—１，当n＝１时，a１＝S１＝５不适合上式．∴a n＝错误!（２）∵S n＝３a n＋１，１∴n≥２时，S n—１＝３a n. ２１—２得S n—S n—１＝３a n＋１—３a n，∴３a n＋１＝４a n，∴错误!＝错误!，又a２＝错误!S１＝错误!a１＝错误!.∴n≥２时，a n＝错误!·错误!错误!，不适合n＝１．∴a n＝错误!数列通项公式的求法１定义法，即直接利用等差数列或等比数列的定义求通项的方法叫定义法，这种方法适用于已知数列类型的题目.２已知S n求a n.若已知数列的前n项和S n与a n的关系，求数列{a n}的通项a n可用公式,求解.３累加或累乘法,形如a n—a n—１＝f n n≥２的递推式，可用累加法求通项公式；形如错误!＝f n n≥２的递推式，可用累乘法求通项公式.２．设数列{a n}是首项为１的正项数列，且a n＋１—a n＋a n＋１·a n＝0（n∈N*），求{a n}的通项公式．[解] ∵a n＋１—a n＋a n＋１·a n＝0，∴错误!—错误!＝１．又错误!＝１，∴错误!是首项为１，公差为１的等差数列．故错误!＝n.∴a n＝错误!.等差（比）数列的判定【例３】数列{n n１n＋１n*（１）设b n＝a n＋１—２a n，求证：{b n}是等比数列；（２）设c n＝错误!，求证：{c n}是等差数列．思路探究：分别利用等比数列与等差数列的定义进行证明．[证明] （１）a n＋２＝S n＋２—S n＋１＝４a n＋１＋２—４a n—２＝４a n＋１—４a n.错误!＝错误!＝错误!＝错误!＝２．因为S２＝a１＋a２＝４a１＋２，所以a２＝５．所以b１＝a２—２a１＝３．所以数列{b n}是首项为３，公比为２的等比数列．（２）由（１）知b n＝３·２n—１＝a n＋１—２a n，所以错误!—错误!＝３．所以c n＋１—c n＝３，且c１＝错误!＝２，所以数列{c n}是等差数列，公差为３，首项为２．等差数列、等比数列的判定方法１定义法：a n＋１—a n＝d常数⇔{a n}是等差数列；错误!＝q q为常数，q≠0⇔{a n}是等比数列.２中项公式法：２a n＋１＝a n＋a n＋２⇔{a n}是等差数列；a\o\al（２,n＋１）＝a n·a n＋２a n≠0⇔{a n}是等比数列.３通项公式法：a n＝kn＋b k，b是常数⇔{a n}是等差数列；a n＝c·q n c，q为非零常数⇔{a n}是等比数列.４前n项和公式法：S n＝An２＋Bn A，B为常数，n∈N*⇔{a n}是等差数列；S n＝Aq n—A A，q为常数，且A≠0，q≠0，q≠１，n∈N*⇔{a n}是等比数列.提醒：１前两种方法是判定等差、等比数列的常用方法，而后两种方法常用于选择、填空题中的判定.２若要判定一个数列不是等差比数列，则只需判定其任意的连续三项不成等差比即可.３．数列{a n}的前n项和为S n，若a n＋S n＝n，c n＝a n—１．求证：数列{c n}是等比数列．[证明] 当n＝１时，a１＝S１.由a n＋S n＝n，１得a１＋S１＝１，即２a１＝１，解得a１＝错误!.又a n＋１＋S n＋１＝n＋１，２２—１得a n＋１—a n＋（S n＋１—S n）＝１，即２a n＋１—a n＝１，３因为c n＝a n—１，所以a n＝c n＋１，a n＋１＝c n＋１＋１，代入３式，得２（c n＋１＋１）—（c n＋１）＝１，整理得２c n＋１＝c n，故错误!＝错误!（常数）．所以数列{c n}是一个首项c１＝a１—１＝—错误!，公比为错误!的等比数列.数列求和[探究问题]１．若数列{c n}是公差为d的等差数列，数列{b n}是公比为q（q≠１）的等比数列，且a n＝c n＋b n，如何求数列{a n}的前n项和？[提示] 数列{a n}的前n项和等于数列{c n}和{b n}的前n项和的和．２．有些数列单独看求和困难，但相邻项结合后会变成熟悉的等差数列、等比数列求和．试用此种方法求和：１２—２２＋３２—４２＋…＋99２—１00２.[提示] １２—２２＋３２—４２＋…＋99２—１00２＝（１２—２２）＋（３２—４２）＋…＋（99２—１00２）＝（１—２）（１＋２）＋（３—４）（３＋４）＋…＋（99—１00）（99＋１00）＝—（１＋２＋３＋４＋…＋99＋１00）＝—５0５0．３．我们知道错误!＝错误!—错误!，试用此公式求和：错误!＋错误!＋…＋错误!.[提示] 由错误!＝错误!—错误!得错误!＋错误!＋…＋错误!＝１—错误!＋错误!—错误!＋…＋错误!—错误!＝１—错误!＝错误!.【例４】已知数列{a n}的前n项和S n＝kc n—k（其中c、k为常数），且a２＝４，a6＝8a３.（１）求a n；（２）求数列{na n}的前n项和T n.思路探究：（１）已知S n，据a n与S n的关系a n＝错误!确定a n；（２）若{a n}为等比数列，则{na n}是由等差数列和等比数列的对应项的积构成的新数列，可用错位相减法求和．[解] （１）当n≥２时，a n＝S n—S n—１＝k（c n—c n—１），则a6＝k（c6—c５），a３＝k（c３—c２），错误!＝错误!＝c３＝8，∴c＝２．∵a２＝４，即k（c２—c１）＝４，解得k＝２，∴a n＝２n.当n＝１时，a１＝S１＝２．综上所述，a n＝２n（n∈N*）．（２）na n＝n·２n，则T n＝２＋２·２２＋３·２３＋…＋n·２n，２T n＝１·２２＋２·２３＋３·２４＋…＋（n—１）·２n＋n·２n＋１，两式作差得—T n＝２＋２２＋２３＋…＋２n—n·２n＋１，T n＝２＋（n—１）·２n＋１.１．（变结论）例题中的条件不变，（２）中“求数列{na n}的前n项和T n”变为“求数列{n＋a n}的前n项和T n”．[解] 由题知T n＝１＋２＋２＋２２＋３＋２３＋…＋n＋２n＝（１＋２＋３＋…＋n）＋（２＋２２＋…＋２n）＝错误!＋错误!＝２n＋１—２＋错误!.２．（变结论）例题中的条件不变，将（２）中“求数列{na n}的前n项和T n”变为“求数列错误!的前n项和T n”．[解] 由题知T n＝错误!＋错误!＋错误!＋…＋错误!，１错误!T n＝错误!＋错误!＋…＋错误!＋错误!，２１—２得：错误!T n＝错误!＋错误!＋错误!＋…＋错误!—错误!＝错误!—错误!＝１—错误!n—错误!，∴T n＝２—错误!—错误!＝２—错误!＝２—错误!.数列求和问题一般转化为等差数列或等比数列的前n项和问题或已知公式的数列求和，不能转化的再根据数列通项公式的特点选择恰当的方法求解．一般常见的求和方法有：（１）公式法：利用等差数列或等比数列前n项和公式．（２）分组求和法：把一个数列分成几个可以直接求和的数列．（３）裂项（相消）法：有时把一个数列的通项公式分成两项差的形式，相加过程消去中间项，只剩有限项再求和．（４）错位相减法：适用于一个等差数列和一个等比数列对应项相乘构成的数列求和．（５）倒序相加法：例如，等差数列前n项和公式的推导．。