第二十三章旋转同步测试(zxp)

第23章旋转单元测试题2一、选择题（每小题3分，共33分）1．下列正确描述旋转特征的说法是（）A．旋转后得到的图形与原图形形状与大小都发生变化．B．旋转后得到的图形与原图形形状不变，大小发生变化．C．旋转后得到的图形与原图形形状发生变化，大小不变．D．旋转后得到的图形与原图形形状与大小都没有变化．2．下列描述中心对称的特征的语句中，其中正确的是（）A．成中心对称的两个图形中，连接对称点的线段不一定经过对称中心B．成中心对称的两个图形中，对称中心不一定平分连接对称点的线段C．成中心对称的两个图形中，对称点的连线一定经过对称中心，但不一定被对称中心平分D．成中心对称的两个图形中，对称点的连线一定经过对称中心，且被对称中心平分3.右边的图案是由下面五种基本图形中的两种拼接而成，这两种基本图形是（）A．①⑤B．②④C．③⑤D．②⑤4．下列图形中即是轴对称图形，又是旋转对称图形的是（）A．（l）（2）B．（l）（2）（3）C．（2）（3）（4）D．（1）（2）（3（4）5．下列图形中，是中心对称的图形有（）①正方形；②长方形；③等边三角形；④线段；⑤角；⑥平行四边形。

A．5个 B．2个 C．3个 D．4个6．在平面直角坐标系中，点P（2，—3）关于原点对称的点的坐标是（）A．（2，3） B．（—2，3） C．（—2，—3） D．（—3，2）7．将图形按顺时针方向旋转900后的图形是( )8．将一图形绕着点O顺时针方向旋转700后，再绕着点O逆时针方向旋转1200，这时如果要使图形回到原来的位置，需要将图形绕着点O什么方向旋转多少度？（）A、顺时针方向500B、逆时针方向500C、顺时针方向1900D、逆时针方向19009．如图所示，图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是（）A．l个 B．2个C．3个D．4个10．如图，把图①中的△ABC 经过一定的变换得到图②中的，如果图①中△ABC上点P的坐标为，那么这个点在图②中的对应点的坐标为（）A ．B ．C ．D ．11．下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的，每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的，旋转的角度为（）A．︒30 B．︒60 C．︒120 D．︒180二、填空题（每小题3分，共21分）12．一条线段绕其上一点旋转90°与原来的线段位置关系．13．下列大写字母A，B，C，D，E，F，G，H，I，J，K，L，M，N，O，P，Q，R，S，T，U，V，W，X，Y，Z旋转90°和原来形状一样的有，旋转180°和原来形状一样的有．14．钟表的分针匀速旋转一周需要60分钟，它的旋转中心是____________，经过20分钟，分针旋转了____________。

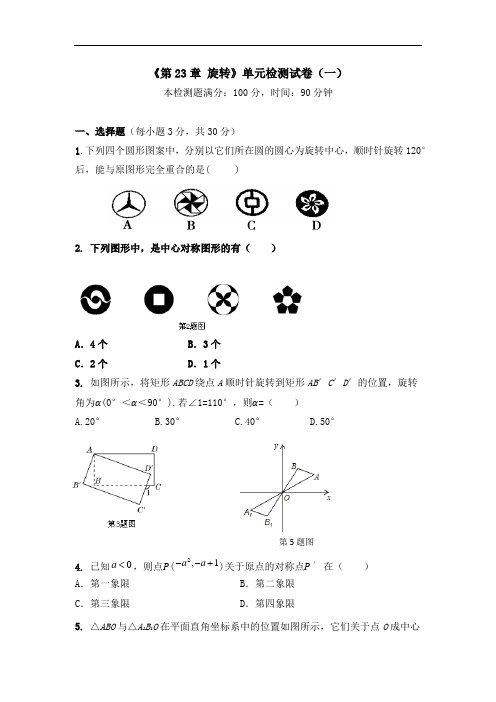
《第23章旋转》单元检测试卷（一）本检测题满分：100分，时间：90分钟一、选择题（每小题3分，共30分）1.下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是( )2.下列图形中，是中心对称图形的有（）A．4个 B．3个C．2个 D．1个3.如图所示，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α(0°＜α＜90°).若∠1=110°，则α=（）A.20°B.30°C.40°D.50°4.已知0a<，则点P(2,1a a--+)关于原点的对称点P′在（）A．第一象限 B．第二象限C．第三象限 D．第四象限5.△ABO与△A1B1O在平面直角坐标系中的位置如图所示，它们关于点O成中心第5题图对称，其中点A（4，2），则点A1的坐标是（）A．（4， -2） B．（-4，-2） C．（-2，-3） D．（-2，-4）6.下列命题中是真命题的是( )A.全等的两个图形是中心对称图形B.关于中心对称的两个图形全等C.中心对称图形都是轴对称图形D.轴对称图形都是中心对称图形7.四边形ABCD的对角线相交于点O，且AO BO CO DO===，则这个四边形（）Ａ.仅是轴对称图形Ｂ.仅是中心对称图形Ｃ.既是轴对称图形又是中心对称图形Ｄ.既不是轴对称图形，又不是中心对称图形8.如图所示，A，B，C三点在正方形网格线的交点处.若将△ACB绕着点A逆时针旋转到如图位置，得到△AC′B′，使A，C，B′三点共线，则旋转角为( )A. 30°B. 60°C. 20°D. 45°9.如图，△AOB为等腰三角形，顶点A的坐标为（2，5），底边OB在x轴上．将△AOB绕点B按顺时针方向旋转一定角度后得△A'O'B，点A的对应点A'在x轴上，则点O'的坐标为（）A．（203，103） B．（163，45） C．（203，45） D．（163，43）第9题图10.如图所示，在正方形网格中，将△ABC 绕点A 旋转后得到△ADE ，则下列旋转方式中，符合题意的是（ ）A.顺时针旋转90°B.逆时针旋转90°C.顺时针旋转45°D.逆时针旋转45° 二、填空题（每小题3分，共24分）11.如图所示，把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转，使得点A 落在CB 的延长线上的点E 处，则∠BDC 的度数为_____ ．12.正方形是中心对称图形，它绕它的中心旋转一周和原来的图形重合________次．13.如图，在正方形ABCD 中，AD =1，将△ABD 绕点B 顺时针旋转45°得到 △A BD ''，此时A D ''与CD 交于点E ，则DE 的长度为 .14.边长为 4 cm 的正方形ABCD 绕它的顶点A 旋转180°，顶点B 所经过的路线长为______cm .15. 如图所示，设 P 是等边三角形ABC 内任意一点， △ACP ′是由△ABP 旋转得到的， 则PA _______PB +PC ( 填>、< 或＝ )16. 点(34)P -，关于原点对称的点P ′的坐标为________. 17.已知点P （−b ，2）与点Q （3，2a ）关于原点对称，则a +b 的值是_______.18.直线3y x =+上有一点P(3,n )，则点P 关于原点的对称点P ′为________. 三、解答题（共46分）19．（6分）如图所示，在Rt △OAB 中，90OAB ∠=︒，6OA AB ==，将△OAB 绕点O 沿逆时针方向旋转90︒得到△OA 1B 1．（1）线段1OA 的长是 ，1AOB ∠的度数是 ； （2）连接1AA ，求证：四边形11OAA B 是平行四边形.20．（6分）找出图中的旋转中心，说出旋转多少度能与原图形重合？并说出它是否是中心对称图形．21.（6分）如图所示，网格中有一个四边形和两个三角形． （1）请你画出三个图形关于点O 的中心对称图形；（2）将（1）中画出的图形与原图形看成一个整体图形，请你写出这个整体图形对称轴的条数， 这个整体图形至少旋转多少度与自身重合？22. （6分） 如图，在Rt△ABC 中，∠ACB ＝90°，点D ，F 分别在AB ，AC 上，CF ＝CB ．连接CD ， 将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF ． (1)求证：△BCD ≌△FCE ； (2)若EF ∥CD ，求∠BDC 的度数．23.（6分）图①②均为76⨯的正方形网格，点A ，B ，C 在格点上．（1）在图①中确定格点D ，并画出以A ，B ，C ， D 为顶点的四边形，使其为轴Ｏ第20题图第21题图O对称图形．（画出一个即可）（2）在图②中确定格点E，并画出以A，B，C，E为顶点的四边形，使其为中心对称图形．（画出一个即可）24.（8分）如图所示，将正方形ABCD中的△ABD绕对称中心O旋转至△GEF的位置，EF交AB于点M，GF交BD于点N．请猜想BM与FN有怎样的数量关系？并证明你的结论．25.（8分）如图所示，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）.（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C;平移△ABC，若点A的对应点A2的坐标为（0，-4），画出平移后对应的△A2B2C2.(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标. （3）在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标.第24题图GACBDEFONM参考答案1.A 解析：根据旋转的性质，结合图形的特征，观察发现选项A 以所在圆的圆心为旋转中心，顺时针旋转120°后能与原图形完全重合.2.B 解析：第一、二、三个图形都是中心对称图形，第四个图形是轴对称图形3.A 解析：本题考查了矩形的性质、对顶角和四边形的内角和.如图所示，设BC 与C ′D ′交于点E .因为∠D ′AD +∠BAD ′=90°，所以∠BAD ′=90°-α. 因为∠1=110°，所以∠BED ′=110°. 在四边形ABED ′中，因为∠BAD ′+∠B +∠BED ′+∠D ′=360°，所以90°-α+90°+110°+90°=360°，所以α=20°.4.D 解析：∵ 当a <0 时，点P(−a 2，−a +1)在第二象限， ∴ 点P 关于原点的对称点P ′在第四象限.5.B 解析：∵点A 和点A 1关于原点对称，A （4，2），∴点A 1的坐标是（-4，-2）.6.B 解析：由中心对称图形和轴对称图形的定义知，选项B 正确.7.Ｃ 解析：因为AO BO CO DO ===，所以四边形ABCD 是矩形.8.D 解析：由图易知旋转角为45°.9.C 解析：如图所示，第9题答图过点O '作x D O ⊥'轴，过点A 作x AE ⊥轴， ∵点A 的坐标为()52，，.325,2,52222=+=+=∴==∴）（OE AE AO OE AE∵ OB =O B '=2OE =4，∴.52542121=⨯⨯=•=AE OB S AOB △ ∵AB =AO =3，∴ A 'B =AB =3.,354,5221='∴='•'=∴''D O D O B A S B O A △ ∴点O '的纵坐标为.354 ,38980144)354(42222=-=-='-'=D O O B BD 320384=+=+=∴BD OB OD ，∴ 点O '的坐标为.354,320)(10.B 解析：根据图形可知：∠BAD =90°，所以将△ABC 绕点A 逆时针旋转90°可得到△ADE ．故选B ．11.15° 解析：由题意得∠CBD =150°，BC =BD ，所以∠BDC =15°. 12. 4 解析：正方形的两条对角线的夹角为90°，且对角线分正方形所成的4个小三角形都全等. 13.2解析：根据旋转的性质得到A D CD ''=.又DA E D CE ''∠=∠，A ED CED ''∠=∠，∴ △A ED '≌△CED '，∴ DE D E '=，A E CE '=，由AD =1求出BD设DE =x ，则1A E CE x '==-，1A D '=-，在Rt△A ED '中，根据勾股定理列出方程)()22211x x =-+-，解得2x =14.4π 解析：∵ AB =4 cm ，∴ 顶点B 绕顶点A 旋转180°所经过的路径是个半圆弧，∴ 顶点B 所经过的路线长为4πcm.15. < 解析：连接PP ′，由旋转的性质知，AP =AP ′，BP =CP ′，∠BAP =∠CAP ′,所以∠PAP ′=∠BAC =60°,所以△PAP ′是等边三角形，所以PA =PP ′,所以PB +PC =PC +CP ′> PP ′=PA .16.(34)-， 解析：两个点关于原点对称时，它们的横、纵坐标符号分别相反，所以点P ′的坐标为(34)-，.17.2 解析：∵ 点P （−b ，2）与点Q （3，2a ）关于原点对称，∴3,1b a ==-，∴ 2a b +=.18.（−3，−6） 解析：将点P(3,n )代入3y x =+，得6n =，∴ 对称点P ′为（−3，−6）. 19.（1）6，135°（2）证明：11190AOA OA B ∠=∠=︒， ∴11//OA A B ．又11OA AB A B ==，∴ 四边形11OAA B 是平行四边形．20.解：图中的旋转中心就是该图的几何中心，即点Ｏ．该图绕旋转中心Ｏ旋转90180270360，，，，都能与原来的图形重合，因此，它是一个中心对称图形．21.解：（1）如图所示.（2）2条对称轴，这个整体图形至少旋转180°与自身重合．22. （1）证明：∵ 将线段CD 绕点C 按顺时针方向旋转90°后得CE ， ∴ CD =CE ，∠DCE =90°.∵∠ACB =90°，∴∠BCD =90°－∠ACD =∠FCE . 在△BCD 和△FCE 中，,,,CB CF BCD FCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴△BCD ≌△FCE ．（2）解：由（1）可知△BCD ≌△FCE ，∴ ∠BDC =∠E . ∵ EF ∥CD ，∴ ∠E =180°－∠DCE =90°，∴ ∠BDC =90°． 23.解：（1）如图①所示； （2）如图②所示.24.解：BM =FN .证明如下：在正方形ABCD 中，BD 为对角线，O 为对称中心, ∴ BO =DO ,∠BDA =∠DBA =45°．∵ △GEF 为△ABD 绕点O 旋转所得，∴ FO =DO,∠F =∠BDA ， ∴ BO =FO ，∠OBM =∠OFN . 在 △OBM 和△OFN 中,∠BOM =∠FON ，OB =OF ，∠OBM =∠OFN ，∴ △OBM ≌△OFN ，∴ BM =FN . 25. 解：(1)画出△A 1B 1C 与△A 2B 2C 2如图所示. （2）旋转中心的坐标为(32，−1). (3)点P 的坐标为（-2，0）.提示：作点B 关于x 轴的对称点B ′，其坐标为（0，-4），连接AB ′，则与x 轴的交点就是所求的点P ，求得经过A (-3，2)，B ′(0，-4)两点的直线的解析式为y =－2x －4，该直线与x 轴的交点坐标为（-2，0），故点P 的坐标为（-2，0）.点拨：平移、旋转作图时，只需把多边形的各个顶点等关键点的对应点作出，再顺次连成多边形即可.《第23章旋转》单元检测试卷（二）一、选择题：（每题3，共30分）1．在下列现象中：①时针转动，②电风扇叶片的转动，③转呼啦圈，④传送带上的电视机，其中是旋转的有（）A．①②B．②③ C．①④D．③④2、我们知道，国旗上的五角星是旋转对称图形，它需要旋转多少度后才能与自身重合？（）A、36°B、60°C、45°D、72°3、如果两个图形可通过旋转而相互得到，则下列说法中正确的有( )．①对应点连线的中垂线必经过旋转中心．②这两个图形大小、形状不变．③对应线段一定相等且平行．④将一个图形绕旋转中心旋转某个定角后必与另一个图形重合．A．1个 B．2个 C．3个 D．4个4．下列各图中，既可经过平移，又可经过旋转，由图形①得到图形②的是（）A ．B ．C ．D ．5．在平面直角坐标系中，点A （﹣2，1）与点B 关于原点对称，则点B 的坐标为（ ） A ．（﹣2，1）B ．（2，﹣1）C ．（2，1）D ． （﹣2，﹣1）6．在平面直角坐标系中，把点P （﹣5，3）向右平移8个单位得到点P 1，再将点P 1绕原点旋转90°得到点P 2，则点P 2的坐标是（ ） A ．（3，﹣3）B ．（﹣3，3）C ．（3，3）或（﹣3，﹣3） D ．（3，﹣3）或（﹣3，3）7．如图，边长为2的正方形ABCD 的对角线相交于点O ，过点O 的直线分别交边AD 、BC 与E 、F 两点，则阴影部分的面积是（ ） A ．1 B ．2C ．3D ． 48．如图，将△ABC 绕点C （0，1）旋转180°得到△A'B'C ，设点A的坐标为(,)a b ，则点A'的坐标为（ ） A ．(,)a b -- B ．(,1)a b --- C ．(,1)a b --+ D ．(,2)a b --+9．如图，如果正方形ABCD 旋转后能与正方形CDEF 重合，那么图形所在平面内，可作为旋转中心的点个数（ ）A ．1个B ．2个C ．3个D ．4个10、如图，在Rt △ABC 中，∠ACB =90°，∠A =30°，AC =43，BC 的中点为D ．将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ，EF 的中点为G ，连接DG ．在旋转过程中，DG 的最大值是（ ） A ．43 B ．6 C ．2＋23 D ．8二、填空题：（每题3，共30分）11、如图1，Rt△AOB绕着一点旋转到△A′∠A′O∠A′OB′的位置，可以看到点A旋转到点A′，OA旋转到OA′，∠AOB旋转到∠A′OB′，这些都是互相对应的点、线段和角．已知∠AOB＝30°，∠AOB′＝10°，那么点B的对应点是点______；线段OB的对应线段是线段______；∠A的对应角是______；旋转中心是点______；旋转的角度是______度．12、将一个直角三角尺AOB绕直角顶点O旋转到如图3所示的位置，若∠AOD＝110°，则旋转角的角度是______°，∠BOC＝______°．13、正三角形绕中心旋转＿＿度的整倍数之后能和自己重合．14、时钟6点到9点，时针转动了＿＿度．15、如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为．16、如图所示，△ABC中，∠BAC＝120°，∠DAE＝60°，AB＝AC，△AEC绕点A旋转到△AFB的位置；∠FAD＝，∠FBD＝．17．如图，大圆的面积为4π，大圆的两条直径互相垂直，则图中阴影部分的面积的和为_____．18、点A（﹣3，m）和点B（n，2）关于原点对称，则m+n=19．如图，阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形，若点A的坐标是(1，3)，则点M和点N的坐标分别是_____ ,F A20、如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A的对应点A′的坐标是_______．三、解答题：（共60分）21、（8分）如图，在平面直角坐标系中，三角形②、③是由三角形①依次旋转后所得的图形．（1）在图中标出旋转中心P的位置，并写出它的坐标；（2）在图上画出再次旋转后的三角形④．22．(8分)在如图所示的直角坐标系中，解答下列问题：(1)分别写出A，B两点的坐标；(2)将△ABC绕点A顺时针旋转90°，画出旋转后的△AB1C1 .23．（12分）如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC 绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形；（2）当a=150°时，试判断△AOD的形状，并说明理由；（3）探究：当a为多少度时，△AOD是等腰三角形？24．（10分）如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．（1）旋转中心是点，旋转角度是度；（2）若连结EF，则△AEF是三角形；并证明；（3）若四边形AECF的面积为25，DE=2，求AE的长．25．（10分）每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC 的顶点均在格点上， ①写出A 、B 、C 的坐标．②以原点O 为对称中心，画出△ABC 关于原点O 对称的△A 1B 1C 1，并写出A 1、B 1、C 1．26、（12分） 如图1，在ABC △中，ACB ∠为锐角，点D 为射线BC 上一点，联结AD ，以AD 为一边且在AD 的右侧作正方形ADEF ． （1）如果AB AC =，90BAC =∠，①当点D 在线段BC 上时（与点B 不重合），如图2，线段CF BD 、所在直线的位置关系为 ，线段CF BD 、的数量关系为 ；②当点D 在线段BC 的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB AC ≠，BAC ∠是锐角，点D 在线段BC 上，当ACB ∠满足什么条件时，CF BC ⊥（点C F 、不重合），并说明理由．图1图2 C图3E参考答案一、选择：1、A，2、D，3、C，4、D，5、B，6、A，7、A，8、D,9、C，10、B。

九年级数学上册《第二十三章图形的旋转》同步训练题及答案(人教版)学校:___________班级：___________姓名：___________考号：___________一、选择题1．下列图形绕某点旋转90°后，不能与原来图形重合的是（）A． B． C． D．2．如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合，AB//x轴，交y 轴于点P．将△OAP绕点O 顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A的坐标为( )A．(√3，-1) B．(-1，−√3) C．(−√3，-1) D．(1，√3)3．如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是（）A．B．C．D．4．如图所示，将一个含30∘角的直角三角板ABC绕点A逆时针旋转，点B的对应点是点B′，若点B′、A、C在同一条直线上，则三角板ABC旋转的度数是（）A．60∘B．90∘C．120∘D．150∘5．如图，在Rt△ABC中∠ACB=90∘，∠A=60∘，AC=2将△ABC绕点C按逆时针方向旋转得到△A′B′C，此时点A′恰好在边AB上，则点B′与点B之间的距离为（）A．4 B．2√3C．3 D．√36．如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，∠1=26°则∠B的度数为（）A．19°B．26°C．64°D．71°7．如图，将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若AB=2，∠B=60°则CD的长为（）A．1 B．√3C．2 D．2√28．如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF位置．若四边形AECF的面积为36，DE=2则AE的长为（）A．4√2B．2√6C．6 D．2√10二、填空题9．如图，将右边的图案变成左边的图案，是通过变化得到的.10．如图，在△BDE中，∠BDE=90°， BD=4，点D的坐标是( 6，0) ，∠BDO=15°，将 BDE 旋转到△ABC的位置，点C 在 BD上，则旋转中心的坐标为．11．如图，在平行四边形ABCD中，∠A＝75°，将平行四边形ABCD绕顶点B顺时针旋转到平行四边形A1B1C1D1，当C1D1第一次经过顶点C时，旋转角∠ABA1＝．12．如图，在△ABC中∠C=90°，∠B=30°将△ABC绕点A逆时针方向旋转20°得到△ADE，DE 交AB于点F，则∠AFE=°．13．如图，在△ABC中AB=√2，AC=4以C为旋转中心，将线段CB顺时针旋转90°得线段CD，连接AD，则AD的最小值为．三、解答题14．如图，在6×6的方格中，有一格点△ABC（顶点都在小正方形的顶点上）及格点P，按下列要求画格点三角形．（1）在图1中，画出△ABC绕点P顺时针旋转90°后的三角形△A'B'C'．（2）在图2中，画出△ABC绕某一点顺时针旋转90°后的△DEF，且点P在△DEF内（不包括边界）．15．如图，在△ABC中AB=2，BC=3.6，∠B=60°将△ABC绕点A按顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，求CD的长.16．如图，将矩形ABCD绕点C顺时针旋转得到矩形FECG，点B与点E对应，点E恰好落在AD边上，BH⊥CE交于点H，求证：BH=CD.17．如图，P是正方形ABCD内一点，△ABP绕着点B旋转后能到达△CBE的位置．（1）旋转的角度是多少度？（2）若BP=3cm，求线段PE的长．18．如图，在四边形ABCD中AC，BD是对角线，将点B绕点C逆时针旋转60°得到点E，连接AE，BE，CE．（1）求∠CBE的度数；（2）若△ACD是等边三角形，且∠ABC=30°，AB=3，BD=5求BE的长．参考答案1．D2．B3．B4．D5．B6．D7．C8．D9．旋转10．（6−√2，√6）11．30°12．5013．3√214．（1）解：如图1中，△A′B′C′即为所求.（2）解：如图2中，△DEF即为所求．15．解：由旋转的性质可得：AD ＝AB∵∠B ＝60°∴△ABD 是等边三角形∴BD ＝AB ＝2∵AB ＝2，BC ＝3.6∴CD ＝BC －BD ＝3.6－2＝1.6.16．证明：∵四边形ABCD 是矩形∴AD ∥BC ，AB =CD∴∠DEC =∠BCH∵∠D =90°，BH ⊥EC∴∠D =∠BHC由旋转得CE =CB在△EDC 和△CHB 中{∠DEC =∠HCB∠D =∠BHC CE =CB∴△EDC ≌△CHB （AAS ）∴BH =CD .17．（1）解：∵△ABP 绕着点B 旋转后能到达△CBE 的位置 ∴∠ABC 为旋转角．∵四边形ABCD 是正方形∴∠ABC=90°即旋转的角度是90度；（2）解：∵△ABP 绕着点B 旋转后能到达△CBE 的位置 ∴BP=BE=3cm ，∠PBE=∠ABC=90°∴PE =√BP 2+BE 2=√32+32=3√2cm ．18．（1）解：∵将点B 绕点C 逆时针旋转60°得到点E ∴CB =CE ∠BCE =60°∴△BCE 是等边三角形∴∠CBE =60°．（2）解：∵△ACD 是等边三角形∴AC=DC ∴∠ACE=∠DCB又∵CB=CE∴△ACE≅△DCB∴AE=BD ∵BD=5∴AE=5．∵∠CBE=60°∠ABC=30°∴∠ABE=90°∴在Rt△ABE中BE=√AE2−AB2．∵AB=3∴BE=4．。

2024-2025学年人教新版九年级上册数学《第23章旋转》单元测试卷一．选择题（共10小题，满分30分）1．如图，若点M是等边△ABC的边BC上一点，将△AMC绕点A顺时针旋转得到△ANB，连接MN，则下列结论：①∠BMN＝30°；②MN＝AM；③BN∥AM，其中正确的个数有（）A．3个B．2个C．1个D．0个2．把如图所示的五角星图案，绕着它的中心旋转，若旋转后的五角星能与自身重合．则旋转角至少为（）A．30°B．45°C．60°D．72°3．下列图形是中心对称图形的是（）A．B．C．D．4．在平面直角坐标系中，点（1，3）关于原点对称的点的坐标是（）A．（﹣1，﹣3）B．（﹣1，3）C．（1，﹣3）D．（3，1）5．我国杨秉烈先生在上世纪八十年代发明了繁花曲线规画图工具，利用该工具可以画出许多漂亮的繁花曲线，繁花曲线的图案在服装、餐具等领域都有广泛运用．下面四种繁花曲线中，是轴对称图形的是（）A．B．C．D．6．如图，三个完全相同的四边形组成的图案绕点O旋转可以和原图形重合，则旋转角可以是（）A．60°B．90°C．120°D．150°7．将如图所示的图案通过平移后可以得到的图案是（）A．B．C．D．8．李明家有一个时钟，假期间，某天上午他8点整出门锻炼，回家时发现时针刚好旋转了60°，那么李明回家的时间是（）A．9点整B．9点半C．10点整D．10点半9．如图，已知点A（﹣1，0），B（0，2），A与A′关于y轴对称，连结A′B，现将线段A′B以A′点为中心顺时针旋转90°得A'B'，点B的对应点B′的坐标为（）A．（3，1）B．（2，1）C．（4，1）D．（3，2）10．如图，在正方形网格中，A，B，C，D，E，F，G，H，M，N是网格线交点，△ABC与△DEF关于某点对称，则其对称中心是（）A．点G B．点H C．点M D．点N二．填空题（共10小题，满分30分）11．在圆、正六边形、正八边形中，属于中心对称图形的有个．12．在平面直角坐标系中，若点A（a，3）与点B（﹣1，b）于原点对称，则a+b＝．13．时钟从下午3时到晚上9时，时针沿顺时针方向旋转了度．14．如图，点O是矩形ABCD的对称中心，点P，Q分别在边AD，BC上，且PQ经过点O，AB＝6，AP ＝3，BC＝8，点E是边AB上一动点．则△EPQ周长的最小值为．15．如图，方格纸中每个小正方形的边长均为1，已知A（﹣1，3），B（﹣4，4），C（﹣2，1）．（1）画△ABC关于原点成中心对称的△A1B1C1；（2）若第二象限存在点D，使点A、B、C、D构成平行四边形，则D的坐标为．16．如图，在平面直角坐标系中有一个航空母舰的简图．若将该图案各个顶点的纵坐标保持不变，横坐标都减去3，则所得到的新图案是由原图案向平移3个单位长度得到的．17．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n的最小值为．18．如图是由中国结和雪花两种元素组成的一个图案，这个图案绕着它的旋转中心旋转角度α°（0°＜α＜360°）后能够与它本身重合，则角α最小是度．19．如图，小刚利用计算机绘制了一个树叶图案，曲线C1为抛物线的一部分，顶点为A，曲线C2与曲线C1关于直线y＝﹣x对称，点B为点A的对称点，则点B的坐标为．20．如图，O是△ABC内的点，AB＝AC，∠BAC＝90°，∠BOC＝130°，将△AOB绕点A按逆时针方向旋转90°，得到△ADC，连接OD．设∠AOB为α，当△COD为等腰三角形时，α为．三．解答题（共6小题，满分60分）21．如图，这是一个中心对称图形，A为对称中心，若∠C＝90°，∠B＝30°，AC＝1，求BB'的长．22．已知点M（3m﹣2，2m+1），解答下列问题：（1）若点M与（﹣7，﹣7）关于原点对称，求点m的值；（2）若点N（3，9），且直线MN平行于x轴，求点M的坐标．23．如图，在五边形ABCDE中，∠EAB＝∠BCD＝90°，AB＝BC，∠ABC＝α，AE+CD＝DE．（1）将△ABE绕点B顺时针旋转α，画出旋转后的△BCM，并证明D、C、M三点在一条直线上；（2）求证：△EBD≌△MBD．24．如图3×3网格图都是由9个相同的小正方形组成，每个网格图中有3个小正方形已涂上阴影，请在余下的6个空白小正方形中，按下列要求涂上阴影：（1）选取1个涂上阴影，使4个阴影小正方形组成一个轴对称图形，但不是中心对称图形；（2）选取1个涂上阴影，使4个阴影小正方形组成一个中心对称图形，但不是轴对称图形．25．如图，在△ABC中，AB＝BC，点O是AC边上的中点，将△ABC绕着点O旋转180°得到△ACD．（1）求证：四边形ABCD是菱形；（2）如果∠ABC＝30°，BC＝2，求菱形ABCD的面积．26．如图，已知△ABC和△AEF中，∠B＝∠E，AB＝AE，BC＝EF，∠EAB＝25°，∠F＝57°；（1）请说明∠EAB＝∠FAC的理由；（2）△ABC可以经过图形的变换得到△AEF，请你描述这个变换；（3）求∠AMB的度数．参考答案与试题解析一．选择题（共10小题）1．【答案】C2．【答案】D3．【答案】B4．【答案】A5．【答案】C6．【答案】C7．【答案】D8．【答案】C9．【答案】A10．【答案】C二．填空题（共10小题）11．【答案】见试题解答内容12．【答案】﹣2．13．【答案】180．14．【答案】．15．【答案】（1）见解答．（2）（﹣5，2）或（﹣3，6）．16．【答案】左．17．【答案】见试题解答内容18．【答案】60．19．【答案】（﹣2，0）．20．【答案】85°或115°或145°．三．解答题（共6小题）21．【答案】4．22．【答案】（1）m＝3；（2）M（10，9）．23．【答案】（1）画图见解析，证明见解析；（2）见解析．24．【答案】见解析．25．【答案】（1）略；（2）2．26．【答案】见试题解答内容。

九年级数学（人教版）上学期单元试卷（四）(内容：第23章总分：100分)一、选择题（本大题共10小题，每小题３分，共30分）1．下面的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．将左图所示的图案按顺时针方向旋转90°后可以得到的图案是（）3．如图，如果正方形ABCD旋转后能与正方形CDEF重合，那么图形所在的平面内可作旋转中心的点共有（）A．1 个B．2 个 C．3 个D．4个4．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在B′位置，A点落在A′位置，若AC⊥A′B′，则∠BAC的度数是（）A．50°B．60°C．70°D．80°5．如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB＝45°，则∠AOD等于（）Ａ．55°Ｂ．45°Ｃ．40°Ｄ．35°(第3题) (第4题) (第5题)6．如图，O是边长为1的正△ABC的中心，将△ABC绕点O逆时针方向旋转180，得△A1B1C1，则△A1B1C1与△ABC重叠部分（图中阴影部分）的面积为（）A．34B．36C．32D．38（A）（B）（C）（D）CB对称的图形．若点A 的坐标是(1, 3)，则点M 和点N 的坐标分别为（ ） A ．(13)(13)M N ---，，， B ．(13)(13)M N ---，，， C ．(13)(13)M N --，，，D ．(13)(13)M N ---，，，8. 如图是一个中心对称图形，A 为对称中心，若∠C =90°， ∠B =30°，AC =1，则BB '的长为（ ） A ．4 B ．33 C ．332 D ．334(第6题) (第7题) (第8题)9．如图，已知两个全等直角三角形的直角顶点及一条直角边重合，将△ACB 绕点C 按顺时针方向旋转到△A /CB /的位置，其中A /C 交直线AD 于点E ，A /B /分别交直线AD ,AC 于点F ,G ，则旋转后的图中，全等三角形共有（ ） A ．2对B ．3对C ．4对D ．5对10．如下所示的4组图形中，左边图形与右边图形成中心对称的有（ ） A ．1组 B ．2组 C ．3组 D ．4组二、填空题（本大题共4小题，每小题３分，共12分）11．点P （2，3）绕着原点逆时针方向旋转90o 与点P /重合，则P /的坐标为 ______ 。

新人教版数学九下教师用书第二十三章《旋转》测试题（时间：45 分钟，满分：100 分）一、选择题（每小题 5 分，共 30 分）1.时钟上的分针匀速旋转一周需要 60min ，则经过 10min ，分针旋转了（ ）A. 10°B. 20°C. 30°D. 60°2.平面直角坐标系内与点 P （-2,3）关于原点对称的点的坐标是（ ）A. (3，-2)B. (2，3)C. (2，-3)D. (-2，-3)3.如图，把菱形 ABOC 绕点 O 顺时针旋转到菱形 DFOE ，则下列角中不是旋转角的是（ ）A.∠BOFB. ∠AODC. ∠COED. ∠COF4.如图，同学们曾玩过万花筒，它是由三块等宽等长的玻璃片围城的，其中菱形 AEFG 可以看成是把菱形 ABCD 以点 A 为中心（ ）A.逆时针旋转 120°得到B.逆时针旋转 60°得到C.顺时针旋转 120°得到D.顺时针旋转 60°得到5.下列图形中，是轴对称图形而不是中心对称图形的是（ ）A.等边三角形B.矩形C.平行四边形D.菱形6.如图 4×4 的正方形网格中，△MNP 绕某点旋转一定的角度，得到△M1N1P1，其旋转中心是（ ）A. 点 AB. 点 BC. 点 CD. 点 D.二、填空题（每小题 5 分，共 20 分）7.如图， 阴影部分组成的图案既是关于 x 轴成轴对称的图形又是关于坐标原点 O 成中心对称的图形.若点 A 的坐标是（1,3） ，则点 M 和点 N 的坐标分别是_____________________.8.如图，在△ABC 中，∠CAB=70°，在同一平面内将△ABC 绕A 点旋转到△AB ′C ′位置，且CC ′∥AB ，则∠BAB ′的度数是________________.9. 如果规定：在平面内，将一个图形绕着某一点旋转一定的角度（小于周角）后能和自身重合，就称次图 形 为 旋 转 对 称 图 形 . 那 么 下 列 图 形 中 ， 是 旋 转 对 称 图 形 ， 且 有 一 个 旋 转 角 为 60 ° 的 是 _______________________.①正三角形；②正方形；③正六边形；④正八边形.10. 如图，四边形 ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC ，垂足是 E ，若线段 AE=5，则ABCD S 四边形 =______________.三、解答题（第11题，12题每题12分，第13题、第14题每题13 分，共50分）11.如图，不用量角器，在方格纸中画出△ABC 绕点 B 顺时针旋转 90°得到的111A B C ∆（第 11 题） （第 12 题）12.如图，画出△ABC 关于原点O 对称的111A B C ∆，并求出111,,A B C 三点的坐标.13.如图，∠ABC=90°，P 为射线 BC 上任意一点（点P 与点 B 不重合） ，分别以 AB ，AP 为边在∠ABC 的内部作等边△ABE 和△APQ ，连接 QE 并延长交 BP于点 F ，求证：BF=EF.（第 13 题）14.如图，在等腰Rt△ABC 中，∠C=90°，点O 是AB 的中点，边AC 的长为a，将一块边长足够大的三角板的直角顶点放在点O 处，将三角板绕点O旋转，始终保持三角板的直角边与AC 相交，交点为点D，另一条直角边与BC相交，交点为点 E.求证：等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值 a.（第14 题）（四）附加题（10分）15、如图是一个由5个相同的正方形组成的十字形的纸片，把这一纸片沿一条直线裁成两部分，然后把其中的一部分再沿着另一条直线截成两部分，使所得的三部分纸片通过适当的拼接能组成两个并列的全等的正方形．请在图中画出分割线及拼接后的图形．。

第23章旋转一、选择题：本题共10小题，每小题3分，共30分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.下列图形中，既是轴对称图形，又是中心对称图形的是( )A. B.C. D.2.下列图形中，△A′B′C′与△ABC成中心对称的是( )A.B.C.D.3.如图，在8×8的正方形网格中，△ABC绕某点旋转一定的角度，得到△A′B′C′，则旋转中心是点( )A. PB. QC. MD. N4.如图，已知四边形ABCD和四边形EFGH关于点O成中心对称，下列结论错误的是( )A. AD//EHB. ∠ABC=∠EHGC. ∠AOB=∠EOFD. AO=EO5.已知点A(x−2,3)与点B(x+4,y−5)关于原点对称，则y x的值是( )A. 2B. 1C. 4D. 826.如图，△A′B′C′是由△ABC经过平移得到的，△A′B′C′还可以看作是△ABC经过怎样的图形变化得到?下列结论：①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中所有正确结论的序号是( )A. ①④B. ②③C. ②④D. ③④7.如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90∘到△ABF的位置.若四边形AECF的面积为20，DE=2，则AE的长为( )A. 4B. 25C. 6D. 268.如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是( )A. AC=ADB. AB⊥EBC. BC=DED. ∠A=∠EBC9.如图，将△ABC绕点C顺时针旋转90∘得到△EDC.若点A，D，E在同一条直线上，∠ACB=20∘，则∠ADC的度数是( )A. 55∘B. 60∘C. 65∘D. 70∘10.如图，等边三角形ABC的边长为4，点O是△ABC的中心，∠FOG=120∘，绕点O旋转∠FOG，分别交线段AB，BC于D，E两点，连接DE，给出下列四个结论：①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于43;④△BDE的周长的最小值为6.正确结论的个数是( )3A. 1B. 2C. 3D. 4二、填空题：本题共6小题，每小题3分，共18分。

九年级数学上册第二十三章旋转单元测试卷（人教版2024年秋）一、选择题(本题有10小题，每小题3分，共30分)1.中国航天取得了举世瞩目的成就，为人类和平贡献了中国智慧和中国力量，下列是有关中国航天的图标，其文字上方的图案是中心对称图形的是()2．下列说法中正确的有()(1)如果把一个图形绕着一定点旋转后和另一个图形重合，那么这两个图形成中心对称；(2)如果两个图形关于一点成中心对称，那么其对应点之间的距离相等；(3)如果一个旋转对称图形有一个旋转角为120°，那么它不是中心对称图形；(4)如果一个旋转对称图形有一个旋转角为180°，那么它是中心对称图形．A．0个B．1个C．2个D．3个3.（2024重庆期末)如图，在△ABC中，∠BAC＝135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD.当点A，D，E在同一条直线上时，下列结论不正确的是()A．△ABC≌△DEC B．∠ADC＝45°C．AD＝2AC D．AE＝AB＋CD(第3题)(第4题)(第5题)(第7题) 4．如图，将△ABC绕点A逆时针旋转55°得到△ADE，若∠E＝75°且AD⊥BC于点F，则∠BAC的度数为()A．65°B．70°C．75°D．80°5．如图，在平面直角坐标系xOy中，若将△ABC以某点为旋转中心，顺时针旋转90°得到△DEF，其中点C的对应点是F，点A的对应点是D，点B的对应点是E，则旋转中心的坐标是()A．(0，0)B．(1，0)C．(1，－1)D．(2.5，0.5) 6．在平面直角坐标系中，已知点A(2a，a－b＋2)，B(b，a＋2)关于原点对称，则a，b的值是()A．a＝－1，b＝2B．a＝1，b＝2C．a＝－1，b＝－2D．a＝1，b＝－27．如图，以正六边形ABCDEF的顶点C为旋转中心，按顺时针方向旋转，使得新正六边形A′B′CD′E′F′的顶点E′落在直线BC上，则正六边形ABCDEF至少旋转的度数为()A．60°B．90°C．100°D．30°8．如图，点A－1，52，将OA绕点O顺时针旋转90°得到OA′，则点A′的坐标为()A.－1，－52 B.1，52 C.52，1 D.1，－52(第8题)(第9题)(第10题)(第11题)9．如图，已知在正方形ABCD内有一点P，连接AP，DP，BP，将△APD顺时针旋转90°得到△AEB，连接DE，点P恰好在线段DE上，AP＝2，BP＝10，则DP的长度为()A．2 B.6C．22 D.1010．如图，在平面直角坐标系中，四边形OABC的顶点O在原点上，OA边在x 轴的正半轴上，AB⊥x轴，AB＝CB＝2，OA＝OC，∠AOC＝60°.将四边形OABC绕点O逆时针旋转，每次旋转90°，则第2025次旋转结束时，点C 的坐标为()A．(3，3)B．(3，－3)C．(－3，1)D．(1，－3)二、填空题(本题有6小题，每小题4分，共24分)11.镇江是一座底蕴深厚、人文荟萃的历史文化古城，如图是镇江的一个古建筑的装饰物(里面是一个个小等边三角形)，该图形绕旋转中心(点O)至少旋转________度后可以和自身完全重合．12．在平面直角坐标系xOy中，将点A(1，2)绕着旋转中心旋转180°，得到点B(－3，2)，则旋转中心的坐标为__________．13．如图，D是△ABC的边BC的中点，连接AD并延长到点E，使DE＝AD，连接BE.(1)△ADC和________成中心对称；(2)已知△ADC的面积为4，则△ABE的面积是________．(第13题)(第14题)(第15题)(第16题)14.（2023郴州期末)如图，在平面直角坐标系中，平行四边形OABC的顶点A的坐标为(6，0)，顶点C的坐标为(2，2)，若直线y＝mx＋2平分平行四边形OABC的面积，则m的值为________．15.（2024杭州期中)如图，在平面直角坐标系中，Rt△OAB的顶点A(－2，4)在抛物线y＝ax2上，直角顶点B在x轴上．将Rt△OAB绕点O顺时针旋转90°得到△OCD，边CD与该抛物线交于点P，则CP的长为________．16．如图，在Rt△ACB中，∠ACB＝90°，∠ABC＝25°.O为AB的中点，将OA 绕着点O逆时针旋转θ(0°<θ<180°)至OP.(1)当θ＝30°时，∠CBP＝________；(2)当△BCP恰为等腰三角形时，θ的度数为____________．三、解答题(本题有7小题，共66分，各小题都必须写出解答过程)17．(8分)（2023丰台模拟)如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，将△ABC绕点C逆时针旋转得到△DEC，使点A的对应点D落在BC边上，点B的对应点为E，求线段BD，DE的长．18．(8分)已知平面直角坐标系第二象限内的点P(x2＋2x，3)与另一点Q(x＋2，y)关于原点对称，试求x＋2y的值．19．(8分)如图，将△ABC绕点C顺时针旋转90°得到△EDC.若点A，D，E在同一条直线上，∠ACB＝20°，求∠ADC的度数．20．(10分)如图，在Rt△ABC中，∠C＝90°.(1)将△ABC绕点B顺时针旋转90°，画出旋转后的△A′BC′；(2)连接AA′，若AC－BC＝1，AA′＝10，求BC边的长．21．(10分)在如图所示的方格纸中，每个小方格都是边长为1个单位长度的正方形，图①、图②、图③均为顶点在格点上的三角形(每个小方格的顶点叫格点)．(1)在图中，图①经过________变换可以得到图②(填“平移”“旋转”或“轴对称”)；(2)在图中画出图①绕点A逆时针旋转90°后得到的图形；(3)在图中，图③与图②关于某点中心对称，则其对称中心是点________(填“A”“B”或“C”)．22．(10分)（2023北京)在△ABC中，∠B＝∠C＝α(0°＜α＜45°)，AM⊥BC于点M，D是线段MC上的动点(不与点M，C重合)，将线段DM绕点D顺时针旋转2α得到线段DE.(1)如图①，当点E在线段AC上时，求证：D是MC的中点；(2)如图②，若在线段BM上存在点F(不与点B，M重合)满足DF＝DC，连接AF，AE，EF，请写出∠AEF的大小，并证明．23．(12分)某数学兴趣小组在一次综合与实践活动中探究这样一个问题：将足够大的直角三角尺PEF(∠EPF＝90°，∠F＝30°)的顶点P放在等腰直角三角形ABC的斜边AC的中点O处，S△ABC＝4.(1)尝试探究如图①，三角尺PEF的两条直角边分别与△ABC的边AB，BC交于点M，N，当PE⊥AB时，①PM________PN(填“＞”“＜”或“＝”)；②三角尺PEF与△ABC重叠部分的面积为________．(2)操作发现如图②，将三角尺PEF绕点O旋转，在旋转过程中，三角尺PEF的两条直角边分别与△ABC的边AB，BC交于点M，N(点M不与点A，B重合)，PM 与PN相等吗？请说明理由．(3)类比应用在(2)的条件下，三角尺PEF与△ABC重叠部分的面积变化吗？若变化，请说明理由；若不变，请求出重叠部分的面积．答案一、1.C 2.B 3.D 4.B 5.C 6.A 7.B 8.C 9.B10．A 点拨：连接OB ，过点C 作CP ⊥OA ，垂足为P ，如图所示．∵AB ＝CB ，OA ＝OC ，OB ＝OB ，∴△AOB ≌△COB (SSS )．∴∠AOB ＝∠COB ＝12∠AOC ＝30°.在Rt △AOB 中，AB ＝2，∠AOB ＝30°，∴OB ＝2AB ＝4.∴OA ＝OB 2－AB 2＝2 3.∴OC ＝2 3.在Rt △COP 中，∠POC ＝60°，∴∠OCP ＝30°.∴OP ＝12OC ＝3.∴CP ＝OC 2－OP 2＝3.∴点C 的坐标为(3，3)．∵每次旋转90°，360°÷90°＝4，∴每旋转4次为一个循环．∵2025÷4＝506……1，∴第2025次旋转结束时点C 的位置和最开始时点C 的位置相同．∴第2025次旋转结束时，点C 的坐标为(3，3)．故选A.二、11.6012.(－1，2)13.(1)△EDB(2)814.－1415．4－216．(1)40°(2)50°或65°或80°点拨：(1)由题意结合旋转的性质可得OA ＝OB ＝OP ，进而得∠OBP ＝∠OPB ，然后根据三角形外角的性质得到∠OBP＝12∠AOP＝15°，进而求解．(2)连接AP，易得∠APB＝90°.如图①，当BC＝BP时，易证△ABC≌△ABP，∴∠ABP＝∠ABC＝25°，∴∠AOP＝2∠ABP＝50°；如图②，当BC＝PC时，连接CO并延长交PB于H，根据线段垂直平分线的判定得到CH垂直平分PB，求得∠CHB＝90°，再根据等腰三角形的性质及三角形外角的性质易得θ＝80°；如图③，当PB＝PC时，连接OC，易得OB＝OC，延长PO交BC于G，易得PG垂直平分BC，得到∠BGO＝90°，再根据三角形的内角和得到∠BOG ＝65°，∴θ＝65°.综上，θ的度数为50°或65°或80°.三、17.解：根据题意，得△ABC≌△DEC，∴AB＝DE，AC＝DC.∵AC＝3，∴DC＝3.∵BC＝4，∴BD＝1.在Rt△ABC中，根据勾股定理，得AB＝AC2＋BC2＝5，∴DE＝5. 18．解：根据题意，得(x2＋2x)＋(x＋2)＝0，y＝－3.∴x1＝－1，x2＝－2(不符合题意，舍去)．∴x＋2y＝－1＋2×(－3)＝－7.19．解：∵将△ABC绕点C顺时针旋转90°得到△EDC，∴∠DCE＝∠ACB＝20°，∠ACE＝90°，AC＝CE.∴∠E＝∠EAC＝45°.∴∠ADC＝∠E＋∠DCE＝45＋20°＝65°.20．解：(1)如图，△A′BC′即为所求．(2)如图，设BC＝x，则AC＝BC＋1＝x＋1.在Rt△ABC中，AB2＝BC2＋AC2＝x2＋(x＋1)2.由旋转的性质得A′B＝AB，∠ABA′＝90°.在Rt△AA′B中，A′A2＝A′B2＋AB2＝2AB2.因为AA′＝10，所以(10)2＝2[x2＋(x＋1)2]．整理得x2＋x－2＝0.解得x1＝1，x2＝－2(舍去)．所以BC＝1.21．解：(1)平移(2)图①绕点A逆时针旋转90°后得到的图形如图①所示．①(3)C点拨：如图②，连接DE，发现DE和FG相交于点C，所以对称中心是点C.②22．(1)证明：由旋转的性质，得DM＝DE，∠MDE＝2α.∵∠C＝α，∴∠DEC＝∠MDE－∠C＝α.∴∠C＝∠DEC.∴DE＝DC.∴DM＝DC.∴D是MC的中点．(2)解：∠AEF＝90°.证明：如图，延长FE到H，使EH＝FE，连接CH，AH.∵DF＝DC，∴DE是△FCH的中位线．∴DE∥CH，CH＝2DE.∴∠FCH＝∠FDE.∵∠MDE＝2α，∴∠FCH＝2α.∵∠B＝∠ACB＝α，∴∠ACH＝α，AB＝AC.∴∠B＝∠ACH.设DM＝DE＝m，CD＝n，则CH＝2m，CM＝m＋n，DF＝n，∴FM＝DF－DM＝n－m.∵AM⊥BC，AB＝AC，∴BM＝CM＝m＋n.∴BF＝BM－FM＝m＋n－(n－m)＝2m.∴BF＝CH.在△ABF和△ACH ＝AC，B＝∠ACH，＝CH，∴△ABF≌△ACH(SAS)．∴AF＝AH.又∵FE＝EH，∴AE⊥FH.∴∠AEF＝90°. 23．解：(1)①＝②2(2)PM＝PN.理由如下：连接BP.∵△ABC是等腰直角三角形，∴∠ABC＝90°，∠C＝45°，AB＝BC.又∵O是AC的中点，P在O处，∴BP⊥AC，BP＝PC且∠ABP＝∠CBP＝45°.11∴∠CPN ＋∠NPB ＝90°，∠ABP ＝∠C .∵MP ⊥PN ，∴∠BPM ＋∠NPB ＝90°.∴∠BPM ＝∠CPN .在△MPB 和△NPCBPM ＝∠CPN ，＝CP ，MBP ＝∠C ，∴△MPB ≌△NPC (ASA )．∴PM ＝PN .(3)不变．∵S △ABC ＝4，O 是AC 的中点，P 在O 处，∴S △BCP ＝12S △ABC ＝2.由(2)知△MPB ≌△NPC ，∴三角尺PEF 与△ABC 重叠部分的面积＝△MPB 的面积＋△BON 的面积＝△NPC 的面积＋△BON 的面积＝△BCP 的面积＝2.。

2023-2024学年人教版九年级数学上册《第二十三章旋转》同步练习题附答案学校:___________班级：___________姓名：___________考号：___________一、选择题1.观察下列图形，其中既是轴对称又是中心对称图形的是( )2.点A(4，3)经过某种图形变化后得到点B(﹣3，4)，这种图形变化可以是( )A.关于x轴对称B.关于y轴对称C.绕原点逆时针旋转90°D.绕原点顺时针旋转90°3.如图，将木条a，b与c钉在一起，∠1=70°，∠2=50°，要使木条a与b平行，木条a旋转的度数至少是( )A.10°B.20°C.50°D.70°4.将正六边形绕其对称中心旋转后，恰好能与原来的正六边形重合，那么旋转的角度至少是 ( )A.120°B.60°C.45°D.30°5.如图，在方格纸中，△ABC经过变换得到△DEF，则正确的变换是( )A．把△ABC绕点C逆时针方向旋转90°，再向下平移2格B．把△ABC绕点C顺时针方向旋转90°，再向下平移5格C．把△ABC向下平移4格，再绕点C逆时针方向旋转180°D．把△ABC向下平移5格，再绕点C顺时针方向旋转180°6.如图，点O为平面直角坐标系的原点，点A在x轴上，△OAB是边长为4的等边三角形，以O为旋转中心，将△OAB按顺时针方向旋转60°，得到△OA′B′，那么点A′的坐标为( )A.(2，23)B.(－2，4)C.(－2，22)D.(－2，23)7.如图，△ABC中，AB=6，BC=4，将△ABC绕点A逆时针旋转得到△AEF，使得AF∥BC，延长BC交AE于点D，则线段CD的长为( )A.4B.5C.6D.78.如图，在平面直角坐标系中，点A的坐标为(﹣1，3)，以原点O为中心，将点A 顺时针旋转150°得到点A′，则点A′的坐标为( )A.(0，﹣2)B.(1，﹣3)C.(2，0)D.( 3，﹣1)9.如图,在正方形ABCD中,AB＝3,点M在CD的边上,且DM＝1,△AEM与△ADM关于AM 所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )A.3B.2 3C.13D.1510.一副三角板按图1所示的位置摆放．将△DEF绕点A（F）逆时针旋转60°后（图2），测得CG=10cm，则两个三角形重叠（阴影）部分的面积为（）A.75cm2B. (25+253) cm2C.(25+8133) cm2 D. (25+16233) cm211.如图，等边三角形ABC的边长为4，点O是△ABC的中心，∠FOG=120°，绕点O 旋转∠FOG，分别交线段AB、BC于D、E两点，连接DE.给出下列四个结论：①OD=OE；②S△ODE =S△BDE；③四边形ODBE的面积始终等于；④△BDE周长的最小值为6.上述结论中正确的个数是( )A.1B.2C.3D.412.如图,在Rt△ABC中,∠ACB＝90°,将△ABC绕顶点C逆时针旋转得到△A′B′C,M 是BC的中点,P是A′B′的中点,连接PM.若BC＝2,∠BAC＝30°,则线段PM的最大值是( )A.4B.3C.2D.1二、填空题13.在平面直角坐标系中，点P(2，3)与点P′(2a＋b，a＋2b)关于原点对称，则a－b的值为________.14.如图，在△ABC中，∠ACB=90°，AC=BC=1cm，如果以AC的中点O为旋转中心，将△ABC旋转180°，点B落在点D处，连接BD，那么线段BD的长为cm.15.如图，在△ACB中，∠BAC=50°，AC=2，AB=3，现将△ACB绕点A逆时针旋转50°得到△AC1B1，则阴影部分的面积为 .16.如图，在矩形ABCD中，AB=5，BC=3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点A落在矩形ABCD的边CD上，连接CE，则CE的长是 .17.有两个完全重合的矩形，将其中一个始终保持不动，另一个矩形绕其对称中心O 按逆时针方向向进行旋转，每次均旋转45°，第1次旋转后得到图①，第2次旋转后得到图②，…，则第10次旋转后得到的图形是图(填①、②、③、④)18.如图，已知∠MON=120°，点A，B分别在OM，ON上，且OA=OB=a，将射线OM绕点O逆时针旋转得到OM′，旋转角为α(0°＜α＜120°且α≠60°)，作点A关于直线OM′的对称点C，画直线BC交OM′于点D，连接AC，AD.有下列结论：①AD=CD；②∠ACD的大小随着α的变化而变化；③当α=30°时，四边形OADC为菱形；④△ACD面积的最大值为3a2；其中正确的是 .(把你认为正确结论的序号都填上).三、解答题19.如图，在△ABC中，AB＝AC，若将△ABC绕点C顺时针旋转180°得到△EFC，连接AF、BE.(1)求证：四边形ABEF是平行四边形；(2)当∠ABC为多少度时，四边形ABEF为矩形？请说明理由.20.如图，在△ABC中，∠ACB＝90°，AB＝5，BC＝4，将△ABC绕点C顺时针旋转90°，若点A、B的对应点分别是点D、E，请直接画出旋转后的三角形简图(不要求尺规作图)，并求点A与点D之间的距离.21.已知△ABC与△DEC是两个大小不同的等腰直角三角形.(1)如图①所示，连接AE，DB，试判断线段AE和DB的数量和位置关系，并说明理由；(2)如图②所示，连接DB，将线段DB绕D点顺时针旋转90°到DF，连接AF，试判断线段DE和AF的数量和位置关系，并说明理由.22.如图，△ABC是边长为4 cm的等边三角形，边AB在射线OM上，且OA＝6 cm，点D从点O出发，沿OM的方向以1 cm/s的速度运动，当D不与A点重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE，连接DE.(1)求证：△CDE是等边三角形；(2)点D运动时间为t，当6<t<10时，△BDE的周长是否存在最小值？若存在，求出△BDE的最小周长；若不存在，请说明理由；(3)当点D在射线OM上运动时，是否存在以D，E，B为顶点的三角形是直角三角形？若存在，求出此时的值；若不存在，请说明理由．23.已知，在菱形ABCD中，∠ADC＝60°，点H为CD上任意一点(不与C、D重合)，过点H作CD的垂线，交BD于点E，连接AE.(1)如图1，线段EH、CH、AE之间的数量关系是；(2)如图2，将△DHE绕点D顺时针旋转，当点E、H、C在一条直线上时.求证：AE＋EH＝CH.24.如图1，已知∠DAC＝90°，△ABC是等边三角形，点P为射线AD上任意一点(点P与点A不重合)，连接CP，将线段CD绕点C顺时针旋转60°得到线段CQ，连接QB并延长交直线AD于点E.(1)如图1，猜想∠QEP＝°(2)如图2、3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；(3)如图3，若∠DAC＝120°，∠ACP＝15°，且AC＝6，求BQ的长.答案1.D2.C.3.B.4.B5.B6.D.7.B8.D9.C10.C11.C12.B13.答案为：1.14.答案为： 5.15.答案为：π.16.答案为：.17.答案为：②.18.答案为：①③④.19.证明：(1)∵将△ABC绕点C顺时针旋转180°得到△EFC ∴△ABC≌△EFC∴CA＝CE，CB＝CF∴四边形ABEF是平行四边形；(2)解：当∠ABC＝60°时，四边形ABEF为矩形理由是：∵∠ABC＝60°，AB＝AC∴△ABC是等边三角形∴AB＝AC＝BC∵CA＝CE，CB＝CF∴AE＝BF∵四边形ABEF是平行四边形∴四边形ABEF是矩形.20.解：如图∵在△ABC中，∠ACB＝90°，AB＝5，BC＝4∴AC＝3∵将△ABC绕点C顺时针旋转90°，点A，B的对应点分别是点D，E ∴AC＝CD＝3，∠ACD＝90°∴AD＝3 2.21.解：(1)AE＝DB，AE⊥DB证明：∵△ABC与△DEC是等腰直角三角形∴AC＝BC，EC＝DC在Rt△BCD和Rt△ACE中∴Rt△BCD≌Rt△ACE∴AE＝BD，∠AEC＝∠BDC∵∠BCD＝90°∴∠DHE＝90°∴AE⊥DB；(2)DE＝AF，DE⊥AF证明：设DE与AF交于N，由题意得，BE＝AD∵∠EBD＝∠C＋∠BDC＝90°＋∠BDC∠ADF＝∠BDF＋∠BDC＝90°＋∠BDC∴∠EBD＝∠ADF在△EBD和△ADF中∴△EBD≌△ADF∴DE＝AF，∠E＝∠FAD∵∠E＝45°，∠EDC＝45°∴∠FAD＝45°∴∠AND＝90°，即DE⊥AF.22.解：(1)∵将△ACD绕点C逆时针方向旋转60°得到△BCE ∴∠DCE＝60°，DC＝EC∴△CDE是等边三角形；(2)存在，当6＜t＜10时由旋转的性质得，BE＝AD∴C＝BE＋DB＋DE＝AB＋DE＝4＋DE△DBE由(1)知，△CDE是等边三角形∴DE＝CD∴C＝CD＋4△DBE由垂线段最短可知，当CD⊥AB时，△BDE的周长最小此时，CD＝2 3 cm∴△BDE的最小周长＝CD＋4＝23＋4(cm)；(3)存在．①∵当点D与点B重合时，D，B，E不能构成三角形∴当点D与点B重合时，不符合题意；②当0≤t<6时由旋转可知，∠ABE＝60°，∠BDE<60°∴∠BED＝90°由(1)可知，△CDE是等边三角形∴∠DEC＝60°∴∠CEB＝30°.∵∠CEB＝∠CDA∴∠CDA＝30°.∵∠CAB＝60°∴∠ACD＝∠ADC＝30°∴DA＝CA＝4∴OD＝OA－DA＝6－4＝2∴t＝2÷1＝2 s；③当6＜t＜10时，由∠DBE＝120°＞90°∴此时不存在；④当t＞10时，由旋转的性质可知，∠DBE＝60°又由(1)知∠CDE＝60°∴∠BDE＝∠CDE＋∠BDC＝60°＋∠BDC而∠BDC＞0°∴∠BDE＞60°∴∠BDE＝90°，∠BCD＝30°∴BD＝BC＝4∴OD＝14 cm∴t＝14÷1＝14 s综上所述：当t＝2或14 s时，以D，E，B为顶点的三角形是直角三角形．23.解：(1)EH2＋CH2＝AE2如图1，过E作EM⊥AD于M∵四边形ABCD是菱形∴AD＝CD，∠ADE＝∠CDE∵EH⊥CD∴∠DME＝∠DHE＝90°在△DME与△DHE中∴△DME≌△DHE∴EM＝EH，DM＝DH∴AM＝CH在Rt△AME中，AE2＝AM2＋EM2∴AE2＝EH2＋CH2；故答案为：EH2＋CH2＝AE2；(2)如图2，∵菱形ABCD，∠ADC＝60°∴∠BDC＝∠BDA＝30°，DA＝DC∵EH⊥CD∴∠DEH＝60°在CH上截取HG，使HG＝EH∵DH⊥EG，∴ED＝DG又∵∠DEG＝60°∴△DEG是等边三角形∴∠EDG＝60°∵∠EDG＝∠ADC＝60°∴∠EDG﹣∠ADG＝∠ADC﹣∠ADG∴∠ADE＝∠CDG在△DAE与△DCG中∴△DAE≌△DCG∴AE＝GC∵CH＝CG＋GH∴CH＝AE＋EH.24.解：(1)∠QEP＝60°；证明：如图1，QE与CP的交点记为M∵PC＝CQ，且∠PCQ＝60°则△CQB和△CPA中∴△CQB≌△CPA(SAS)∴∠CQB＝∠CPA在△PEM和△CQM中，∠EMP＝∠CMQ∴∠QEP＝∠QCP＝60°.故答案为：60；(2)∠QEP＝60°.以∠DAC是锐角为例.证明：如图2∵△ABC是等边三角形∴AC＝BC，∠ACB＝60°∵线段CP绕点C顺时针旋转60°得到线段CQ ∴CP＝CQ，∠PCQ＝6O°∴∠ACB＋∠BCP＝∠BCP＋∠PCQ即∠ACP＝∠BCQ在△ACP和△BCQ中∴△ACP≌△BCQ(SAS)∴∠APC＝∠Q∵∠BOP＝∠COQ∴∠QEP＝∠PCQ＝60°；(3)作CH⊥AD于H，如图3与(2)一样可证明△ACP≌△BCQ∴AP＝BQ∵∠DAC＝135°，∠ACP＝15°∴∠APC＝30°，∠PCB＝45°∴△ACH为等腰直角三角形∴AH＝CH＝22AC＝3 2在Rt△PHC中，PH＝3CH＝3 6 ∴PA＝PH﹣AH＝36﹣3 2∴BQ＝36﹣3 2.。

第6题图第二十三章 旋转检测题一、 选择题（每小题3分，共30分）1.下面图形中，既是轴对称图形又是中心对称图形的是（ ）2．如果一个四边形ABCD 是中心对称图形，那么这个四边形一定是（ ） A ．等腰梯形 B ．矩形 C ．菱形 D ．平行四边形3．如右上图，四边形ABCD 是正方形，ΔADE 绕着点A 旋转900后到达ΔABF 的位置，连接EF ，则ΔAEF 的形状是（ ）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形 4.已知0a <，则点(2,1a a --+)关于原点的对称点 在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 5.下列命题中是真命题的是( )A.全等的两个图形是中心对称图形B.关于中心对称的两个图形全等C.中心对称图形都是轴对称图形D.轴对称图形都是中心对称图形 6．如图，把图中的△ABC 经过一定的变换得到△A′B′C′，如果图中△ABC 上的点P 的坐标为（a ，b ），那么它的对应点P′的坐标为（ ） A ．（a -2，b ） B ．（a +2，b ） C ．（a -2，-b ） D ．（a +2，-b ）7.四边形ABCD 的对角线相交于O ，且AO BO CO DO ===，则这个四边形（ ）Ａ.仅是轴对称图形 Ｂ.仅是中心对称图形 Ｃ.既是轴对称图形又是中心对称图形 Ｄ.既不是轴对称图形，又不是中心对称图形 8.如图所示，A 、B 、C 三点在正方形网格线的交点处.若将△绕着点A 逆时针旋转到如图位置，得到△，使三点共线，则的值为( )FED CBA陕西省教育科学规划课题《整体优化县域初中数学课堂教学有效策略》（编号：SGH13888）子课题《整体优化县域初中数学试卷讲评课有效策略》教学设计第14题图A. 1B.223C.310D. 2 9.如图所示，在正方形中，，点在上，且，点是上一动点，连接，将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上， 则的长是( )A ．1B ．2C ．3D ．4 10．如图，在Rt △ABC 中，∠ACB =90°，∠A =30°，BC =2．将△ABC 绕点C 按顺时针方向旋转n 度后得到△EDC ，此时点D 在AB 边上，斜边DE 交AC 边于点F ，则n 的大小和图中阴影部分的面积分别为（ ） A ．30，2B ．60，2C ．60，32D ．60， 3二、填空题（本大题共6小题，每小题3分，共18分）11．给出以下4个图形：①平行四边形，②正方形，③等边三角形，④圆．其中，既是轴对称图形又是中心对称图形的是________________（填序号） 12．如图，正方形ABCD 边长为2，E 为CD 的中点，以点A 为中心，把△ADE 顺时针旋转90°得△ABF ，连接EF ，则EF 的长等于__________.13．如图等边三角形AOB ，绕点O 逆时针旋转到△COD 的位置，设旋转角 为α，AC 、BD相交于点E ，AC 与OB 相交于点M ，BD 与OC 相交于点N ，写出图中一对全等的三角形是： ________________（写出一对即可）14．如图，在△ABC 中，∠ACB =90°，AC =BC ，点P 在△ABC 内，△AP ′C 是由△BPC绕着点C 旋转得到的，PA = 5 ，PB =1，∠BPC =135°．则PC =_______________ 15．如图，是4×4的正方形网格，把其中一个标有数字的白色小正方形涂黑，就可以使图中的黑色部分构成一个中心对称图形，则这个白色小正方形内的数字是__________.16．如图，在直角坐标系中，射线OA 与x 轴正半轴重合，以O 为旋转中心将OA 逆时针旋转：OA →OA 1→OA 2→…→OA n …，旋转角∠AOA 1=2°，∠A 1OA 2=4°，∠A 2OA 3=8°，…要求下一个旋转角（不超过360°）是前一个旋转角的2倍．当旋转角大于360°时，又从2°开始旋转，即∠A 8OA 9=2°，∠A 9OA 10=4°，…周而复始．则当OA n 与y 轴正半轴第一次重合时，n 的值为_________________.（提示：2+22+23+24+25+26+27+28=510）第10题图第12题图第13题图三、解答题（共52分）17. (6分)画出△ABC 关于原点O 对称的△A 1B 1C 1，并求出点A 1，B 1，C 1的坐标。