SPC分析实例

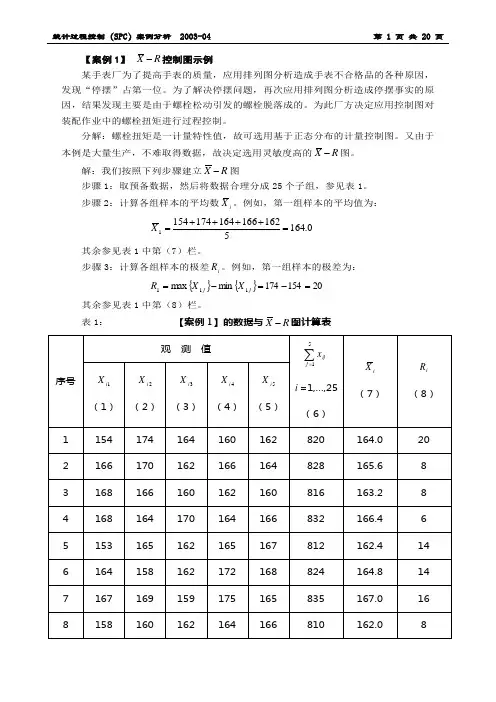
【案例1】 R X -控制图示例某手表厂为了提高手表的质量，应用排列图分析造成手表不合格品的各种原因，发现“停摆”占第一位。

为了解决停摆问题，再次应用排列图分析造成停摆事实的原因，结果发现主要是由于螺栓松动引发的螺栓脱落成的。

为此厂方决定应用控制图对装配作业中的螺栓扭矩进行过程控制。

分解：螺栓扭矩是一计量特性值，故可选用基于正态分布的计量控制图。

又由于本例是大量生产，不难取得数据，故决定选用灵敏度高的R X -图。

解：我们按照下列步骤建立R X -图步骤1：取预备数据，然后将数据合理分成25个子组，参见表1。

步骤2：计算各组样本的平均数i X 。

例如，第一组样本的平均值为：0.16451621661641741541=++++=X其余参见表1中第（7）栏。

步骤3：计算各组样本的极差i R 。

例如，第一组样本的极差为：{}{}20154174min max 111=-=-=j j X X R其余参见表1中第（8）栏。

表1： 【案例1】的数据与R X -图计算表i 故：272.163=X ，280.14=R 。

步骤5：计算R 图的参数。

先计算R 图的参数。

从D 3、D 4系数表可知，当子组大小n =5，D 4=2.114，D 3=0，代入R 图的公式，得到： 188.30280.14114.24=⨯==R D UCLR280.14==R CLR==R D LCLR3—极差控制图：均值控制图：图1 【案例1】 的第一次R X -图13579111315171921232530.18814.280 0.000 135791113151719212325171.512163.272 155.032参见图1。

可见现在R 图判稳。

故接着再建立X 图。

由于n =5，从系数A 2表知A 2=0.577，再将272.163=X ，280.14=R 代入X 图的公式，得到X 图：512.171280.14577.0272.1632≈⨯+=+=R A X UCL X272.163==X CLX032.155280.14577.0272.1632≈⨯-=-=R A X LCLX因为第13组X 值为155.00小于XLCL ，故过程的均值失控。

spc案例SPC（Statistical Process Control，也叫统计过程控制）是一种通过统计方法对产品和过程进行监控和改进的质量管理方法。

下面是一个SPC案例，用以说明其在实际生产中的应用。

某制造公司生产一种产品，经过市场调查发现，该产品存在一定的质量问题，如尺寸偏差、露粉等。

为了解决这些问题，公司决定采用SPC方法来监控和改进生产过程。

首先，公司确定一组关键工艺参数，如温度、压力、转速等，以及相关的质量指标，如尺寸、外观等。

随后，公司对每个工艺参数进行测量和记录，并将其输入到SPC软件中。

同时，公司还设置了对应的上下限值，即规定了每个工艺参数的合理变化范围。

在生产过程中，SPC软件会自动进行统计分析，并生成控制图。

控制图上有一条中心线，表示期望值，以及上下限线，表示允许的变化范围。

同时，还有一些参考线，如标准偏差线，用于判断过程稳定性。

公司的技术人员定期对控制图进行检查，观察各参数是否在规定范围内波动，是否出现异常情况。

如果发现异常，技术人员会及时采取措施，如调整机器参数、更换工具等，以及及时通知相关操作人员。

通过SPC的实施，公司逐渐发现了一些问题。

例如，当温度过高时，产品尺寸会偏大；当压力过低时，产品内部会出现空隙。

公司根据这些发现，对生产过程进行了优化，并引入了更先进的控制系統，进一步提高了产品质量。

此外，SPC还帮助公司进行了质量变化的监控和评估。

公司可以利用SPC软件生成的统计报表，进行不同时间段内产品质量的对比。

同时，公司还可以进行根因分析，找出导致质量问题的根本原因，并提出相应的改进措施。

总的来说，通过SPC的应用，该制造公司有效地改善了产品质量，减少了不合格品的数量，并提高了自身的竞争力。

SPC 方法在实际生产中具有广泛的应用前景，可以帮助企业提升质量管理水平，降低成本，提高效率。

SPC统计过程控制应用实例分析1.SPC控制特性的定义T1S6949质量管理体系在实际应用中强调以系统的方法对过程进行分析研究，以确定系统的输入因子，输出因子以及输入对输出的影响作用。

产品实现的过程也可以用框图简单地描述为下图：上图表示，产品实现的过程为由材料、生产参数、设备、人员、环境构成的输入因素通过生产转换成输出产品的过程，同时利用输出的信息来反作用于输入因素，以得到输入因素如材料、生产参数等的持续改进。

输入因素通过生产过程转化成输出的产品，其中的实现过程也就是SPC需要进行监控的工艺过程，当然针对SPC控制特性的选择并不是越多越好，由于检验本身是不带来增值效益的过程，因此在行业的应用过程中，考虑到成本的计算，SPC只会应用在部分关键特性的监控过程中，而关键特性的选择也根据企业自身的生产能力及控制能力的需要来决定的。

因此在进行统计过程控制时，首先需要定义控制的对象，然后通过监控生产实现过程中的各大因素对控制对象的作用，检测到过程的特殊原因波动，从而实现提前预防不合格品产品的作用。

针对关键特性之外的其他参数，可以通过记录检查表的形式将其记录并保存，以便工艺改进时提供历史依据的参考。

PSC的控制项目对产品特性及工序监控的必要性，通常通过以下几个方面进行考量；(1) 从产品特性要求判断，是否为产品关键特性；如Tirm Form工序，SPC记录共面性的抽样检验结果，以判断产品当前的生产流程是否处于稳定受控的状态下。

产品的关键特性在产品设计阶段己确定。

(2) 另一方面，在产品生产制造的过程中，关键工序参数的监控对产品质量良率起着重大的决定作用，利用实时的SPC方法进行工艺参数的监控，能够及时发现生产过程中存在的特殊原因，及时围堵并消除，以得到立即的改正及预防的作用。

例如，在硅片切割工序(Wafer saw)，工艺上利用对切割槽宽度的定期数据采集，绘制SPC控制图，从而起到过程监控的作用，以防止参数对切割工序带来的过程能力偏移。

SPC案例分析在当今竞争激烈的制造业环境中，质量控制成为了企业生存和发展的关键。

统计过程控制（Statistical Process Control，简称 SPC）作为一种有效的质量控制工具，已经在众多企业中得到了广泛的应用。

本文将通过一个具体的案例，深入探讨 SPC 在实际生产中的应用和效果。

一、案例背景我们选取的案例是一家汽车零部件制造企业，该企业主要生产发动机缸体。

在过去的一段时间里，客户对产品的质量投诉不断增加，主要问题集中在缸体的尺寸精度不符合要求，导致发动机装配过程中出现故障。

为了解决这一问题，企业决定引入 SPC 方法进行质量控制。

二、SPC 方法的实施过程1、确定关键质量特性首先，企业的质量控制团队与生产部门合作，通过对产品设计要求和客户反馈的分析，确定了发动机缸体的关键质量特性，即缸体的内径尺寸和圆柱度。

2、数据采集在生产过程中，质量控制人员每隔一定时间从生产线上抽取一定数量的缸体样本，使用高精度测量仪器对关键质量特性进行测量，并记录测量数据。

3、控制图的绘制将采集到的数据输入到统计软件中，绘制均值极差控制图（XR 控制图）和均值标准差控制图（XS 控制图）。

控制图的横坐标表示样本序号，纵坐标表示测量值。

4、控制限的确定根据样本数据的分布特征和统计规律，计算出控制图的控制限。

控制限分为上控制限（UCL）、下控制限（LCL）和中心线（CL）。

中心线通常为样本数据的均值，上控制限和下控制限则根据一定的计算公式得出。

5、过程监控与分析定期对控制图进行观察和分析，判断生产过程是否处于受控状态。

如果数据点落在控制限内，且没有明显的趋势或异常模式，则认为过程处于受控状态；反之，如果数据点超出控制限，或者出现连续上升或下降的趋势，或者存在周期性的波动等异常模式，则认为过程失控，需要采取相应的措施进行改进。

三、案例结果与分析在实施 SPC 方法后的一段时间里，企业对生产过程进行了持续的监控和分析。

）案例分析统计过程控制（SPC用途一．态。

统计控制状产过程处于分析判断生产过程的稳定性，生1.防不合格品异，预缓慢变．及时发现生产过程中的异常现象和2产生。

术精度，以便作出正确的技备的实际艺．查明生产设备和工装3决定。

质量提供依据。

品为评定产．4二、控制图的设计原理分态值服从或近似服从正：设绝大多数质量特性正态性假三1布。

则：准73%9932三?发生的。

小概率事件原理：小概率事件一般是不会三3证法思想。

反三4控制图的种类四．~）量值（按产品质量的特性分（）计11三SXRXRXRX ,,,????S。

图）（数值，，，（）计up2cpn图。

）分析用控制图；（）控制用控制按控制图的用途分：（212三控制图的判断规则五．：分析用控制图三1种情况）；绝大多数点子在控制界限线内（准判规则稳则1-----3。

现象（规则种情况）排列无下述则判异准-----28-1--1-：图控制用控制三2每一个点子均落在控制界限内。

规则1现象。

控制界限内点子的排列无异常规则2量程产过质图元件的不合格率而为案例控制某无线电设计，生2][p 。

平均不合格率要求为≤2%-2--2-收集收据解：一.见程中收集数据准化的情况下从生产过在充分固定并标,,5M1E下表所表示:元件不合格品率数据表线电某无值平均711 1.4k本中不合格品率样计算二:.i列在上表?p.,k,i?1,2,.....,n i i 程平均不合格品率过三求:.?k i140%248/17775???p?n i-3--3-140%??p CL图线四计算控制:.p n/3p(1UCL?p??)p i n/p?3)p(1UCL??pi化而变时随的从上式可以看出当诸样本大小不相等,UCL,LCL, nn ii变化其图形为阶梯式的折线而非直线为了方便若有关系式:,,.n?2n max n?n/2min同时满足也即相差不大时可以令使得上下限仍为常数其图,,,,,nnn?ii形仍为直线.本例中诸样本大小满足上面条件故有控制线为:,,,n711n?i CL?p?140%图:p UCL?p?3p(1?p)/n?p?3p(1?p)/n?2.72%图五制作i UCL?p?3p(1?p)/n?p?3p(1?p)/n?0.08%i控制:.以样本序号为横坐标样本不合格品率为纵坐标做图.p,,六描点依据每个样本中的不合格品率在图上描点.:.七分析生产过程是否处于统计控制状态.从图上可以看到第个点超过控制界限上界出现异常现象这说,,14,明生产过程处于失控状态尽管但由于生产过程失控即,.=1.40%<2%,p -4--4-图化为控制用控制不合格品率波动大所以不能将此分析用控制图转,,正措施点失控的原因并制定纠应查明第.,14案例分析造成手表不用排列图量某手表厂为了提高手表的质应3][,用再次应摆占第一位为了解决停摆问题合格的各种原因发现停,---.,而发现主要是由于螺栓脱落造成的分析造成停摆的原因结果排列图,,中的螺装配作业厂方决定应用控制图对后者是有螺栓松动造成为此,.程控制行过栓扭矩进.又由于本例图选用正态分布控制分析螺栓扭矩是计量特征值故可,],[图用灵敏度高的难取得数据故决定选是大量生产不.,,R?x图按照下列步骤建立解][R x?下表见组预备根据合理分组原则取数据步骤一.25,,.X值为例如第一值组样本的平均计步骤二算各样本组的平均.,i X=(154+174+164+166+162)/5=164.01本的极差算各样步骤三计.20X}?174?154???R,Rmax{X}min{i1ii值计算样本总均骤步四.和平均样本极差RX?X?4081.8i?357?Ri所以,X?163.272R?14.280步骤五计算图与的参数.R X先计算图的参数(1)R样本容量时,D4=2.114,D3=0n=5-5--5-UCL?DR?2.114*14.280?30.1884R代入图公式CL?R?14.280R R LCL?DR?03R均值控制图极差控制图X R图计的原始数据与算表例.2备观察值样本X i注序号R∑XijXi5Xi4Xi3Xi2Xi110820164162166164174154．20-6--6-值图。

统计过程控制案例分析统计过程控制案例分析在生产和管理领域，统计过程控制（SPC）是一种重要的技术，用于监控和改善过程质量。

本文通过一个实际案例分析，探讨了SPC的应用和效果。

案例背景某电子产品制造商在生产过程中遇到了质量问题，产品不合格率居高不下。

为了解决这个问题，公司决定采用SPC技术对生产过程进行监控和改进。

控制图分析首先，我们通过控制图来分析生产过程。

控制图是一个直观的图形，横轴表示时间，纵轴表示产品质量。

在SPC中，通常使用X-R图（均值-极差图）来监控过程的稳定性。

X-R图由两条曲线组成，一条表示均值（X），另一条表示极差（R）。

均值反映过程的中心趋势，极差反映过程的波动大小。

通过对X-R图的分析，我们可以发现生产过程中的波动和不稳定性。

在本案例中，我们发现产品质量存在较大的波动，且不合格率较高。

这表明生产过程存在较大的问题，需要进行改进。

原因分析和措施制定针对上述问题，我们进行了深入的原因分析。

通过对生产环节的调查和分析，我们发现问题的主要原因是原材料的质量不稳定。

为此，我们提出了以下改进措施：1、对原材料进行质量检查和控制，确保原材料的质量符合要求。

2、加强生产过程的监控和管理，确保生产过程的稳定性和一致性。

3、提高员工的技能和素质，加强质量意识培训。

实施改进措施在制定改进措施后，我们开始实施。

在实施过程中，我们采用了PDCA 循环（计划-执行-检查-处理）来确保改进措施的有效性和持续性。

在改进措施实施后，我们再次对生产过程进行了SPC监控和评估。

效果评估和总结通过SPC技术的监控和评估，我们发现生产过程的质量得到了显著改善。

不合格率得到了有效降低，产品质量更加稳定。

员工的技能和素质也得到了提高，质量意识得到了加强。

这些改进不仅提高了企业的生产效率和质量水平，也提高了客户对产品的满意度。

通过本案例的分析，我们可以看到SPC技术在生产和管理领域的重要作用。

SPC技术可以帮助我们监控和改善过程质量，提高生产效率和质量水平。

统计过程控制SPC案例分析制造公司生产汽车零件，该公司决定采用统计过程控制来监测生产过程中的变异程度，并及时采取相应的措施来保证产品质量。

首先，该公司确定了需要监控的关键过程参数，如尺寸、重量、硬度等。

然后，选取了一个代表性样本，进行了初始的统计分析。

通过对样本数据的收集和分析，可以得到该过程的中心值（mean）和过程能力指数（process capability index）。

接下来，公司制定了针对每个关键过程参数的控制限规则。

这些规则包括上控制限（Upper Control Limit，UCL）和下控制限（LowerControl Limit，LCL），一旦产品参数超出这些限制范围就会引发警报。

第三步，该公司开始在生产线上收集样本数据，并进行实时统计分析。

每隔一段时间，例如每小时或每一天，取样并测量样本的关键参数，记录数据并计算统计指标，例如平均值和标准差。

最后，根据统计分析的结果，如果数据超出了控制限范围，该公司可以立即采取纠正措施。

例如，如果平均值偏离了中心值，可以调整生产设备或工艺参数；如果数据的变异过大，可以对生产设备进行维护或调整操作程序。

通过持续的SPC监测和改进，该公司可以实现以下几方面的益处：1.提高质量：通过监测关键参数并及时纠正异常，可以减少产品的次品率和退货率，提高产品质量，满足客户需求。

2.降低成本：通过减少次品率和退货率，公司可以降低废品处理成本和退货成本；此外，通过减少变异，还可以降低废品和工时成本。

3.提高效率：通过监控关键参数，公司可以及时调整生产设备或工艺参数，减少无效生产时间和停机时间，提高生产效率和产能。

需要注意的是，SPC并非一劳永逸的解决方案，而是需要持续不断的监测和改进。

公司应该定期复评统计指标，根据实际情况调整控制限并更新纠正措施。

此外，为了提高SPC的效果，公司还可以使用一些辅助工具，如散点图、控制图和直方图等，帮助分析和解决问题。

综上所述，统计过程控制是一种有效的管理技术，可以帮助制造公司提高质量、降低成本和提高效率。

经典的SPC应用的例子俗话说宴无好宴。

朋友邀我去他家做客吃晚饭，进了门迎面遇上他焦急无辜的表情，才知道主题是咨询。

起因是朋友最近回家的时间越来越晚，罪证就在他家门口玄关的那张纸上朋友的太太是一家美商独资企业的QC主管，在家里挂了一张单值-移动极差控制图，对朋友的抵家时间这一重要参数予以严格监控：设定的上限是晚七点，下限是晚六点，每天实际抵家时间被记录、描点、连线最近连续七天(扣除双休日)的趋势表明，朋友抵家的时间曲线一路上扬，甚至最近两天都是在七点之后才到家的，证据确凿按照休哈特控制图的原则和美国三大汽车公司联合编制的SPC(Statistical Quality Control，统计过程控制)手册的解释，连续7点上升已绝对表明过程发生了异常，必须分析导致异常的原因并做出必要的措施(比如准备搓衣板)，使过程恢复正常。

显然，我可能给出的合理解释成了朋友期待的救命稻草，而这顿晚饭就是他在我面前挂着的胡萝卜。

显然，朋友的太太比我们绝大多数的企业家更专业(当然，作为同类，我想这也许就是导致我们只能成为管理工具的原因)，她清楚地认识到：预防措施，永远比事后的挽救更重要。

顺便说一句，朋友太太厨艺很优秀，属于那种下得厨房上得厅堂的模范太太当然，对朋友的在意程度更是显而易见的，否则不会选择抵家时间作为重要的过程特性予以控制这个过程参数，在她眼里，无疑昭示着忠诚度。

饭后上了红酒，席间的谈话就从过程异常的判定开始。

"我们先来陈述一下控制图的判异准则：第一，出现任何超出控制限的点；第二，出现连续7点上升或者下降或者在中心线的一边；第三，出现任何明显非随机的图形。

显然，目前该过程已经符合其中第一和第二项，确实出现了异常。

作为过程控制的责任者，你打算怎么分析呢？'"还是我们传统的分析方法：因果图。

'"那么，我们寻找的还是这五个方面的原因了：人、机、料、法、环？"是的。

统计过程控制（SPC）案例分析一．用途1.分析判断生产过程的稳定性，生产过程处于统计控制状态。

2．及时发现生产过程中的异常现象和缓慢变异，预防不合格品产生。

3．查明生产设备和工艺装备的实际精度，以便作出正确的技术决定。

4．为评定产品质量提供依据。

二、控制图的设计原理1．正态性假设：绝大多数质量特性值服从或近似服从正态分布。

2． 3 准则： 99。

73%。

3．小概率事件原理：小概率事件一般是不会发生的。

4．反证法思想。

四．控制图的种类1．~S）按产品质量的特性分（1）计量值（X R, X R, X R S, X（2）计数值（ p，pn，u，c 图）。

2．按控制图的用途分：（1）分析用控制图；（2）控制用控制图。

五．控制图的判断规则1．分析用控制图：规则 1判稳准则-----绝大多数点子在控制界限线内（ 3 种情况）；规则 2判异准则 -----排列无下述现象（ 8 种情况）。

2．控制用控制图：规则 1每一个点子均落在控制界限内。

规则 2控制界限内点子的排列无异常现象。

[案例 2]为控制某无线电元件的不合格率而设计 p 图，生产过程质量要求为平均不合格率≤2%。

解：一 .收集收据在 5M1E 充分固定并标准化的情况下 ,从生产过程中收集数据 ,见下表所表示 :某无线电元件不合格品率数据表组号样本大小样本中不合格品数不合格品率18358 1.0280812 1.5378060.8450412 2.4586014 1.6660050.8782211 1.388148 1.0961810 1.6107038 1.11185019 2.21270911 1.61370010 1.41450016 3.21583014 1.71679870.9178139 1.11881870.9195818 1.4205506 1.12180711 1.4225957 1.22350012 2.42476070.92562010 1.6总和17775248平均值711 1.4二.计算样本中不合格品率 : p i k i,i 1,2,....., k 列在上表.n i,三.求过程平均不合格品率 :p k i248 / 17775140% n iCL p140%四.计算控制线p 图:UCL p3p(1p) / n iUCL p3p(1p) / n i从上式可以看出 ,当诸样本大小n i不相等时 ,UCL,LCL 随n i的变化而变化 ,其图形为阶梯式的折线而非直线.为了方便 ,若有关系式 :n max2nn min n / 2同时满足 ,也即n i相差不大时可以令n i n使得上下限仍为常数,其图,,,形仍为直线 .本例中 , n711 ,诸样本大小n i满足上面条件,故有控制线为: CL p140%p 图:UCL p3p(1p) / n i p3p(1p) / n 2.72%UCL p3p(1p) / n i p3p(1p) / n0.08%五.制作控制图 :以样本序号为横坐标 ,样本不合格品率为纵坐标 ,做 p 图.UCLCLLCL六.描点 :依据每个样本中的不合格品率在图上描点.七.分析生产过程是否处于统计控制状态从图上可以看到 ,第 14 个点超过控制界限上界 ,出现异常现象 ,这说明生产过程处于失控状态 .尽管p=1.40%<2%,但由于生产过程失控,即不合格品率波动大,所以不能将此分析用控制图转化为控制用控制图,应查明第 14 点失控的原因 ,并制定纠正措施 .[案例 3]某手表厂为了提高手表的质量,应用排列图分析造成手表不合格的各种原因 ,发现 ---停摆占第一位 .为了解决停摆问题 ,再次应用排列图分析造成停摆的原因 ,结果发现主要是由于螺栓脱落造成的,而后者是有螺栓松动造成 .为此 ,厂方决定应用控制图对装配作业中的螺栓扭矩进行过程控制 .[ 分析 ]螺栓扭矩是计量特征值,故可选用正态分布控制图,又由于本例是大量生产 ,不难取得数据 ,故决定选用灵敏度高的x R 图.[解]按照下列步骤建立x R 图步骤一 .根据合理分组原则 ,取 25 组预备数据 ,见下表 .步骤二 .计算各样本组的平均值X i,例如第一组样本的平均值为X1=(154+174+164+166+162)/5=164.0步骤三 .计算各样本的极差R i , R1max{ X i } min{ X i } 174 154 20步骤四 .计算样本总均值X和平均样本极差RX i4081.8R i357所以 , X 163.272R 14.280步骤五 .计算 R 图与X的参数(1)先计算 R 图的参数样本容量 n=5 时,D4=2.114,D3=0UCL R D4 R 2.114 * 14.280 30.188代入 R 图公式CL R R 14.280LCL R D3 R0均值控制图极差控制图例 2 的原始数据与X R 图计算表.样本观察值X i 备序号Xi1Xi2Xi3Xi4Xi5∑ Xij R注1154174164166162820164． 0202166170162166164828165． 683168166160162160816163． 284168164170164166832166． 465153165162165167812162． 4146164158162172168824164． 8147167169159175165835167． 0168158160162164166810162． 089156162164152164798159． 61210174162162156174828165． 61811168174166160166934166． 81412148160162164170804160． 82213165159147153151775155． 018超限14164166164170164828165． 6615162158154168172814162． 81816158162156164152792158． 41217151158154181168812162． 43018166166172164162830166． 01019170170166160160826165． 21020168160162154160804160． 81421162164165169153813162． 61622166160170172158826165． 21423172164159165160822164． 01324174164166157162823164． 61725151160164158170803160． 619∑4081． 8357平均163． 27214． 280（2）可见现在 R 图判稳，故接着再建立均值图。