当前位置：文档之家 › 六年级下册数学课件《6、立体图形的表面积和体积1》苏教版34

六年级下册数学课件《6、立体图形的表面积和体积1》苏教版34

  • 格式：pptx
  • 大小：946.62 KB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

六年级数学下册立体图形的表面积和体积苏教版ppt课件

六年级数学下册立体图形的表面积和体积苏教版ppt课件

有志者自有千方百计，无志者只感千难万难。 虽长不满七尺，而心雄万丈。
S
活动要求：每组选定一个物h 体进行研究。
算一一个算 立：体选图择形合所适有ɑ的面条的件总b列面式积解决问题，组长搜集。
h
表面积=侧面积+底面积×2
把一盒优酸乳倒入一个底面积为62平方厘米，高为6厘米的圆锥形水杯中，正好倒满2杯。
把一个正方体的木头削成一个最大的圆柱，这根木ɑ 头的利用率是百分之几？
你看到了哪些形体？
整理与反思
整理与反思
它们之间有怎样的联系？ 20×4×20=1600(cm2) 活动要求：每组选定一个物体进行研究。 cm2 dm2 m2 … 一个棱长是6分米的正方体，它的表面积和 体积各是多少？ 雄心志四海，万里望风尘。 志气和贫困是患难兄弟，世人常见他们伴在一起。 圆锥的体积 = 底面积 ×高×× 想一想：这些体积公式可以怎样分类？ 一个棱长是6分米的正方体，它的表面积和 体积各是多少？ 大丈夫处世，不能立功建业，几与草木同腐乎? 60×25=1500(cm2) 大丈夫处世，不能立功建业，几与草木同腐乎? 不要志气高大，倒要俯就卑微的人。 活动要求：每组选定一个物体进行研究。
每平方米收5千克蔬菜， 每千克售3.6元。
活动要求：每组选定一个物体进行研究。 1.想一想：我能解决这个物体的什么问题，组长记录。 2.算一算：选择合适的条件列式解决问题，组长搜集。 3.说一说：在小组里说一说自己的想法。
练习与实践
பைடு நூலகம்
你想怎样加工这根木头？
14×（8÷2）2×12 大丈夫处世，不能立功建业，几与草木同腐乎? 圆锥的体积是与它等底等高的圆柱体积的 。 250ml（±5ml） 活动要求：每组选定一个物体进行研究。 不要志气高大，倒要俯就卑微的人。 义务教育教科书小学数学六年级下册 一个棱长是6分米的正方体，它的表面积和 体积各是多少？

六年级数学下册课件立体图形的表面积和体积苏教版36(共15张PPT)

六年级数学下册课件立体图形的表面积和体积苏教版36(共15张PPT)

（
）
识体系。 4、一个长方体金鱼缸，长40厘米，宽40厘米，高35厘米。
底面半径10cm 高6cm 把一根圆柱形木料削成一个最大的圆锥，削去部分的体积是圆锥体积的(
)。
(1)一间卧室地面的面积是15(
)。
2、什么是物体的体积？什么是容器的容积？常用的体积单位有哪些？相邻单位间的进率各是多少？
5 C. 把一块铁块从这个容器的水中取出后，水面下降2厘米。
学习目标： 棱长是6厘米的正方体，表面积和体积相等。
一个长方体的纸盒，将它展开后，得到什么样的图形？
一个长方体的纸盒，将它展开后，得到什么样的图形？
1、理解并掌握立体图形的 （
）
2、什么是物体的体积？什么是容器的容积？常用的体积单位有哪些？相邻单位间的进率各是多少？
一个圆柱和一个圆锥等底等高，它们的体积相差12立方分米，这个圆柱的体积是（ ）立方分米，圆锥的体积是（ ）立方分米。
一个长方体
上
的纸盒，将
它展开后，
得到什么样
的图形？
左
后
右
下 前
底面
底面
底面
底面周长
底面
圆
柱
的
高
表
面
展
开
图
填表
挑战第一关
制作一个圆柱形的油桶，至少需要多 少铁皮，是求圆柱形油桶的（ ）。
挑战第二关 棱长是6厘米的正方体，表面积
和体积相等。（ ）
挑战第三关 一个圆柱和一个圆锥等底等高，它 们的体积相差12立方分米，这个圆柱
长4m 宽3m 高2m
棱长是6厘米的正方体，表面积和体积相等。
2、正确、灵活应用公式进
行计算。
小组合作交流： 1、什么是长方体、正方体和圆 柱的表面积？各怎样计算？ 2、什么是物体的体积？什么是 容器的容积？常用的体积单位有 哪些？相邻单位间的进率各是多 少？

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》(6) (共19张PPT)

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》(6) (共19张PPT)
积。
表面积： π×10×5=50π（平方厘米） π×（10÷2）2×2=50π（平方厘米） 50π＋50π=100π（平方厘米） 体积： π×（10÷2）2 ×5=125π（立方厘米）
4.求下面立体图形的体积。
（1）一个正方体，底面周长是 8 dm。 （8÷4）3= 8（立方分米）
答：正方体的体积是8立方分米。
（2）一个长方体，底面是边长12cm 的正方形，高是50cm。
12×12×50 = 7200（立方厘米） 答：长方体的体积是7200立方厘米。
4.求下面立体图形的体积。
（3）一个圆柱，底面周长是 12.56 cm，高是 5 cm。 12.56÷3.14÷2 =2（厘米）
7. 制作下面的圆柱形物体，至少各需要多少铁皮？
油桶
底面半径4dm 高12dm
水桶
底面直径40cm 高50cm
通风管
管口周长0.628m 长1.2m
0.628×1.2=0.7536（平方米） 答：制作这个通风管至少需要0.7536平方米铁皮。
谢 谢！
•不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年4月9日星期六2022/4/92022/4/92022/4/9 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/92022/4/92022/4/94/9/2022 •正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/4/92022/4/9April 9, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
体积是指物体所占空间的大小。容积是指容器所能容纳 物体的多少。计量物体的体积要从物体的外部测量数据， 而计量容积通常要从容器的内部测量数据。

六年级下册数学PPT-《6、立体图形的表面积和体积(1)》苏教版(14张)-精品课件

六年级下册数学PPT-《6、立体图形的表面积和体积(1)》苏教版(14张)-精品课件

四、生活中的数学问题
一个圆锥形状的土堆，底面周长314米，高1.5 米。这堆土有多少立方米？
314÷3.14÷2=50(米）
3.14×502×1.5× 1
3
=3.14×1250 =3925(立方米） 答：这堆土有3925立方米。
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
4分米
表面积：
表面积：
6×6×6
2×3.14×1.5×4＋3.14×1.5²×2
体积： 6×6×6
体积： 3.14× 1.5²×4
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
× ×
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
一、基本练习。 求下面各图形的表面积和体积。（只列式，不计算）
1.5分米
5米 8米
5米
表面积：
5×8×2＋5×5×2+8X5X2
(8X5+8X5+5X5)X2 体积：
8X5×5
6厘米
六年级下册数学PPT-《6、立体图形的 表面积 和体积 （1） 》苏教 版(14张 )-ppt 精品课 件(实用 版)
？ 想一想
1.ห้องสมุดไป่ตู้把一根长3m，底面直径2 dm的 圆柱形钢管截3段，表面积增加了 多少?

苏教版六年级下册数学《立体图形的表面积和体积》课件

苏教版六年级下册数学《立体图形的表面积和体积》课件

h h
r
ab
V = πr² h V = abh
柱体 V = Sh
a aa
V =aaa
三个立体图形的表面积是否可以用同一个公式来计算？
侧面积
Байду номын сангаас
侧面积
侧面积
表面积=侧面积+2个底面积 侧面积=底面周长×高
（15×9+9×5+15×5）×2
5
15
9
3.14×3²×5
6×6×6
6 6
6
把下面的长方体木料削成一个最大的圆锥， 削成的圆锥体积是多少？(单位：cm)
6 4
12
vsh柱体表面积侧面积2个底面积侧面积侧面积侧面积侧面积底面周长高三个立体图形的表面积是否可以用同一个公式来计算
点
点动成线
面动成体
线动成面
1、说一说，你整理了立体图形的哪些知识点。 2、晒一晒，你运用了什么方法进行整理。 3、议一议，你更喜欢哪一种整理方法。
三个立体图形的体积是否可以用同一个公式来计算？

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》 (共14张PPT)

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》 (共14张PPT)

三、对号入座
▪ 一个圆柱形水池，直径是20米，深2米。 （1）这个水池占地面积是（ ）平方米 （2）挖这个水池，共需挖土（ ）立方米
？ （3）在池内的侧面和池底抹一层水泥，水
泥面的面积是（ ）平方米？
四、生活中的数学问题
一个圆锥形状的土堆，底面周长314米，高1.5 米。这堆土有多少立方米？
314÷3.14÷2=50(米）
谢谢观赏
You made my day!
我们，还在路上……
s a
h 长×宽×高
b V=abh
长方体
V=sh
正方体的体积= a 棱长×棱长×棱长
a V=a³
a
正方体
V=sh
圆柱的体积= h 底面积×高
V=sh
s
圆锥体积= 1 ×底面积×高
3
圆锥体
长方体、 正方体、 圆柱体的体积=
底面பைடு நூலகம்×高
V= 1 sh
3
V=sh
圆柱体
立体图形的表面积和体积有什么区别?
(1)表示的意义不同 (2)计量的单位不同 (3)计算的方法不同
a
h
hb a
a a
r
长方体表面积= (ab+ah+bh) ×2
正方体表面积= 6a2
圆 柱 侧 面 积 = 2лrh 圆 柱 表 面 积 = 2лrh+ 2лr 2
油漆桶
无盖水桶
烟筒
油漆桶表面积＝侧面积＋底面积X2
无盖水桶表面积＝侧面积＋底面积
烟筒（通风管）表面积＝侧面积
……
立体图形体积计算
长方体的体积=
全课小结：
1、通过这节课的学习，你有什么收获？ 2、关于立体图形的表面积和体积你还有什么问题？

苏教版六年级下册数学课件-《6、立体图形的表面积和体积(1)》 (共34张PPT)

苏教版六年级下册数学课件-《6、立体图形的表面积和体积(1)》 (共34张PPT)

圆锥体积的推导过程
圆锥的体积=底面积×高×13
圆锥体积的推导过程
---------------
结论：圆柱体积是等底等
高 圆锥体积的3倍 ，圆锥
体积是等底等高圆柱体积
的 。13
圆锥的体积=底面积×高×
1 3
小结
h
a
b
V = abh
a a
a
V = a3
h s
V
V=
1
3
sh
学校在操场边的空地上挖了一个长6米、宽3米、深4分
米的坑，准备装满沙作为沙坑使用。它的旁边有一堆圆
锥形的沙堆，底面积是12.56平方米，高1.5米。这堆沙
够用吗？
4分米=0.4米
能装沙子的体积：6×3×0.4=7.2（立方米）
沙堆的体积:12.56×1.5×
1 3
=6.28(立方米）
7.2立方米 ＞ 6.28立方米
。2021年3月10日星期三2021/3/102021/3/102021/3/10
• •
THE END 15、会当凌绝顶，一览众山小。2021年3月2021/3/102021/3/102021/3/103/10/2021
16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/3/102021/3/10March 10, 2021
2、什么是物体的体积？什么是容器的容积？
物体所占空间的大小叫做物体的体积。 容器所能容纳物体的体积叫做物体的容积。
3、长方体，正方体，圆柱体，圆锥的体积计算公式是 什么？它们是怎么推导出来的？
长方体的体积公式推导过程
4厘米
2 厘 米
3厘米
长方体的体积＝长×宽×高
正方体体积的推导过程

苏教版六年级下册数学课件-《6、立体图形的表面积和体积》 (共19张PPT)

苏教版六年级下册数学课件-《6、立体图形的表面积和体积》 (共19张PPT)

• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
THE END 17、一个人如果不到最高峰，他就没有片刻的安宁，他也就不会感到生命的恬静和光荣。2021/3/102021/3/102021/3/102021/3/10
谢谢观看
等积变形
荷花池是圆柱形的，底面半径是5米，高2米，把 挖出的土堆成一堆，请问： （1）这堆土的体积是多少立方米？ （2）如果把这堆土用来填一个长方体的坑，长方 体坑长10米，宽2米，可以铺多厚？
切割塑形
把一个棱长6分米的正方体木块，削 成一个最大的圆柱，这个圆柱的体积 是多少？如果削成圆锥，体积是多少？
。2021年3月10日星期三2021/3/102021/3/102021/3/10
15、会当凌绝顶，一览众山小。2021年3月2021/3/102021/3/102021/3/103/10/2021
16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2021/3/102021/3/10March 10, 2021
10、人的志向通常和他们的能力成正比例。2021/3/102021/3/102021/3/103/10/2021 12:52:59 PM 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/3/102021/3/102021/3/10Mar-2110-Mar-21 12、越是无能的人，越喜欢挑剔别人的错儿。2021/3/102021/3/102021/3/10Wednesday, March 10, 2021 13、志不立，天下无可成之事。2021/3/102021/3/102021/3/102021/3/103/10/2021

最新苏教版数学六年级下册《立体图形的表面积和体积》ppt课件1

最新苏教版数学六年级下册《立体图形的表面积和体积》ppt课件1

a a a
V = a3
h a b h h
V = abh
s
V = sh V=
s
1
V = sh
3
sh
a
h b
a
2
a a
h
r
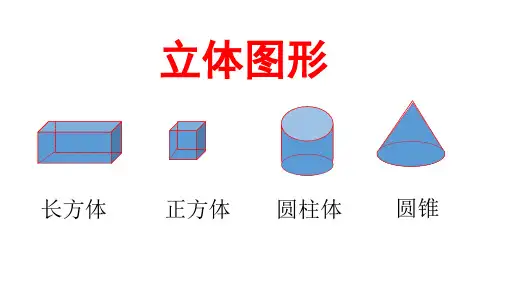
长方体3;bh) ×2
圆柱侧面积= 圆柱表面积=
6a 2лrh 2лrh+ 2лr
2
立体图形的表面积和体积有什么区别?
(1)表示的意义不同 (2)计量的单位不同
(3)计算的方法不同
1、只列式，不计算： 1)一个长方体,它的长是4分米,宽是5分 米,高是2分米,求它的表面积和体积. 2)一个棱长是6分米的正方体,它的表面 积和体积各是多少？ 3)一个圆柱的底面半径是3厘米,高12厘 米,求它的表面积和体积. 4)一个圆锥的底面周长是62.8厘米,高 是15厘米,它的体积是多少立方厘米?
4、你能解决下面生活中的问题吗?
1)一个圆柱形水池,直径是20米,深2米. ①这个水池占地面积是多少? 3.14×(20÷2)2 ②挖成这个水池,共需挖土多少立方米? 3.14×(20÷2)2 ×2 ③在池内四周和池底抹一层水泥,水泥 面的面积是多少平方米? 3.14×20×2+3.14×(20÷2)2
我们是如何学习正方体的体积的。
正方体的体积＝棱长3
我们是如何学习圆柱体积的。
拼成的长方体的与 原来的圆柱体比较，什 么变了？什么没变？
体积
底面积 高
公式
圆柱体积 ＝ 底面积 × 高
长方体体积 ＝ 底面积 × 高
我们是如何学习圆锥体积的。
结论：圆柱体积是等底等高 圆锥体积 的3倍 ，圆锥体积是等底等高圆柱体积 的 1 3
3

苏教版六年级下册数学立体图形的表面积和体积 (课件)

苏教版六年级下册数学立体图形的表面积和体积 (课件)

知识闯关
一个圆柱的侧面积是80平方厘米，底面半径是3 厘米，它的体积是多少立方厘米？
六棱柱
发挥想象
…… ？
六棱柱课堂总结创造长源自体判断哪个可以折成普通长方体?
创造正方体
思考：怎样的长方形纸可以折成正方体?
创造圆柱
①如果长方形纸的长是12.56厘米,宽是9.42厘米,卷成的圆柱高是多少? ②如果为这两个圆柱配个底面,该如何配?
创造圆柱
创造圆柱
创造直柱体
创造直柱体
直柱体
知识闯关
想一正想方，体上的面表三面个积图和形体中积，（（ ））体积最大。 A.长A方.一体样大 B.正B方.不体一样大 CC.圆.无锥法比较
立体图形的表面积和体积 复习
苏教版版六年级下册
教学目标
1.在操作活动中进一步认识长方体、正方体、圆柱、圆锥等立体图形的特征，经 历探索立体图形表面积、体积有关知识的过程，并能运用知识解决实际问题。 2.在活动探索中进一步体会知识之间的内在联系,培养观察、比较和归纳整理的能 力,发展空间观念,增强立体思维。 3. 在活动思考中进一步感受数学知识、方法之间的内在联系，体验与同学合作交 流以及获取知识的乐趣,增进对数学学习的积极情感。
回顾梳理
活动一：
1.有序交流，回忆相关知识，由 组长统一填写在知识回忆卡上。 2.合理分工，准备汇报。
回顾梳理
图形
表面积
体积
创造物体
活动二： （1）用提供的长方形纸创造立体图形。 （2）组内交流创造方法，说说长方形和立体图 形的联系。
创造长方体
12厘米 20厘米
20厘米 12厘米
①长方形和折成的立体图形有哪些相通点? ②比较：两个长方体哪个表面积大?

六年级下册数学课件《6、立体图形的表面积和体积1》苏教版53

六年级下册数学课件《6、立体图形的表面积和体积1》苏教版53

六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53 六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53 六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
苏教版六年级下册
立体图形表面积和体积的复习
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
理一理
图形
表面积
联系
体积
联系
h ab
a aa
rh
h r
S 2(ab ah bh)
S 6a2
S Ch 2r2
这些立体图形的体积公式都是怎样得出来的？结合图片在 小组里讨论一下。
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
等底等高
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
圆锥体体积的推导过程
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53
h r
联系
体积
联系
V abh
V a3
V r 2h
V 1 sh 3
直柱体
V sh
理一理
长方体和正方体的表面积也可以用侧面积+2个 底面积来计算吗？
侧面积
侧面积
侧面积
表面积=侧面积+2个底面积 侧面积=底面周长×高
六年级下 册数学 课件《6 、立体 图形的 表面积 和体积 1》苏 教版53

六年级下册数学精品课件 - 6、立体图形的表面积和体积 苏教版(34页PPT)

六年级下册数学精品课件 - 6、立体图形的表面积和体积 苏教版(34页PPT)

等底等高
等底等高
等底等高
当圆柱与圆锥等底
等高时，圆锥的体
积是圆柱的（
1 3
）
1 圆锥体积=底面积×高× 3
直柱体
图形
表面积
Байду номын сангаас
体积
S表=(ab+ah+bh)×2 V=abh
S表=6a2
V=a3
S表=S侧+2S底
( S侧=Ch)
V=Sh
1
V= 3Sh
图形
表面积 S表=(ab+ah+bh)×2
7 、 构件吊装和翻身扶直时的吊点必须符合 设计规 定。异 型构件 或无设 计规定 时，应 经计算 确定， 并保证 使构件 起吊平 稳。 8 、 安装所使用的螺栓、钢楔（或木楔）、 钢垫板 、垫木 和电焊 条等的 材质应 符合设 计要求 的材质 标准及 国家现 行标准 的有关 规定。
9 、 吊装大、重、新结构构件和采用新的吊 装工艺 时，应 先进行 试吊， 确认无 问题后 ，方可 正式起 吊。
3 、所有过度加热的混合料均废弃。 拌和后 的混合 料均匀 一致， 无花白 、无粗 细料离 析或结 团现象 。 4 、材料的规格或配合比发生改变时 ，根据 室内试 验资料 进行试 拌。
5 、已经离析或结团、块或在运料车 辆卸料 时滞留 于车上 的混合 料，以 及低于 规定铺 筑温度 或被雨 淋湿的 混合料 均废弃 。运至 铺筑现 场的混 合料， 应及时 压实。 6 、 高空吊装屋架、梁和斜吊法吊装柱时， 应于构 件两端 绑扎溜 绳，由 操作人 员控制 构件的 平衡和 稳定。
立体图形表面积和体积总复习
图形
表面积
体积
S表=(ab+ah+bh)×2 V=abh

六年级下册数学课件《6、立体图形的表面积和体积(1)》苏教版PPT课件

六年级下册数学课件《6、立体图形的表面积和体积(1)》苏教版PPT课件

六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
苏教版六年级下册
立体图形表面积和体积的复习
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
理一理
图形
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件 六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
直柱体
V sh
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件
六年级下册数学课件《6、立体图形的 表面积 和体积 （1） 》苏教 版PPT课 件

六年级数学下册课件-7.2.6立体图形的表面积和体积(共34张PPT)213-苏教版

六年级数学下册课件-7.2.6立体图形的表面积和体积(共34张PPT)213-苏教版

28
B.
长方体体积＝底面积×高
＝4（升）
cm3(mL)dm3(L)m3 … （1）做这个鱼缸要用多长的铝合金？ （6）放入的鱼、鹅卵石和水草体积是多少？ 棱长总和:(6+3+4)×4 求圆柱的体积是多少？
V＝abh 答：需要6吨沙子。 像长方体、正方体、圆柱这样两个底面形状相同；
（ 3）做这个鱼缸需要多少玻璃？ 27个铁圆锥, 可以熔铸成等底等高的圆 （4）圆柱底面半径扩大3倍，高不变，它的体积就扩大9倍。 长方体所含小正方体的数量正好
直柱体的体积 = 底面积×高
8米
16平方米
16×8＝128（平方米）
判断下面各题。
（1）压路机的前轮是圆柱形的，轮宽1.6米，直径0.8米，
求前轮滚动一周压路的面积，就是求圆柱的体积。 ×
(
)
（2）一个圆柱削成一个最大的圆锥，削去部分是剩下圆锥体
积的2倍。 …√ (
)
（3）一瓶罐装可口可乐的体积大约是400立方厘米，用24瓶
（1）压路机的前轮是圆柱形的，轮宽1. 这些体积计算公式是怎样得到的？
V锥=13 s h
立体图形 意义
h ab
a aa
r h
h
s
计量单位
体积
物h
V= sh V= 1 sh
3
cm3(mL)dm3(L)m3 …
你知道吗？
像长方体、正方体、圆柱这样两个底面形状相同；两底面 面积相等；两底面相互平行；两底面之间有无数条高，高都相 等的立体图形叫做直柱体。
cm3(mL)dm3(L)m3 …
等于长、宽、高的乘积。
长方体体积＝底面积×高
底面积
高
高
长方体体积＝底面积×高 圆柱体积＝底面积×高

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》(4) (共61张PPT)

苏教版六年级下册数学课件《6、立体图形的表面积和体积(1)》(4) (共61张PPT)
学习目标：
1.我要进一步理解立体图形的表面积和体积 （容积）的意义；
2.我要进一步掌握常用的体积（容积）单位 及其进率，会进行它们之间的简单换算；
3.我要进一步掌握立体图形表面积和体积的 计算方法，并能解决相关的实际问题。
导学单：
小组整理讨论：
1.什么是长方体、正方体和圆柱的表面积？ 各怎样计算？ 2.什么是物体的体积？什么是容器的容积？ 3.常用的体积（容积）单位有哪些？相邻体 积（容积）单位间的进率各是多少？ 4.怎样计算长方体、正方体、圆柱和圆锥的 体积？它们的计算公式各是怎样推导出来的， 推导时几者之间有什么联系？
5
1 3 15 = 5 × 3 × 1
5
2 2
3
12 = 3 × 2 × 2
长方体的体积＝长×宽×高
返回
正方体可以看作 一种长、宽、高 都棱长
正方体的体积=棱长×棱长×棱长
返回
圆柱体的体积＝底面积×高
返回
底面
圆
圆
柱
锥
的
的
高
高
等底等高
第1次
第1次
第1次
第1次
16πcm3＞12πcm3
综合应用，提升思维（必做）
（4）一个长方体花坛，从里面量长10m，宽2m，高0.8m， 四周用砖砌成，砖墙的厚度是0.2米，中间填满泥土。
（1）花坛所占的空间有多大？ （10＋0.2×2）×（2＋0.2×2）×0.8 （2）花坛里大约有泥土多少立方米？
10×2×0.8 （3）需要多少立方米的砖？
表面积增加4cm2 体积减少1cm3
学习目标：
1.我要进一步理解立体图形的表面积和体积 （容积）的意义；
2.我要进一步掌握常用的体积（容积）单位 及其进率，会进行它们之间的简单换算；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

转化
推导体积计算公式
主要利用转化的数学思想方法
立 体 王 国
夯实基础 你能行！
明辨是非
1、用4个完全同样的小正方体，能拼成一个大的正方体。 （ ×）
2、圆锥的体积是与它等底等高长方体体积的三分之一。 （√ ）
3、把一个长方体切成两个相同的小长方体，表面和体积各
是原来的一半。
（×）
4、容器的容积等于它的体积。
答：这堆沙不够用。
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
小结
h
a
b
V = abhLeabharlann a aaV = a3
h s
V = sh
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
V = sh
h
s
V=
1
3
sh
小结
a
h
h
a
b
a a
侧面积+底面积×2
小结
实验、转化
推导体积计算公式
圆柱体体积的推导过程
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆柱体积=底面积×高
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆柱体体积的推导过程
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
联系生活
联系生活
有一个长方体铁块，长6分米，宽3分米，高4分米， 现在要将它铸造成一个高是8分米的圆柱形铁块，这 个圆柱形铁块的底面积是多少？
长方体的体积等于圆柱的体积
长方体的体积：6×3×4=72（立方分米） 圆柱的底面积：72÷8=9（平方分米）
答：这个圆柱形铁块的底面积是9平方分米。
联系生活
学校在操场边的空地上挖了一个长6米、宽3米、深4分
米的坑，准备装满沙作为沙坑使用。它的旁边有一堆圆
锥形的沙堆，底面积是12.56平方米，高1.5米。这堆沙
够用吗？
4分米=0.4米
能装沙子的体积：6×3×0.4=7.2（立方米）
沙堆的体积:12.56×1.5×
1 3
=6.28(立方米）
7.2立方米 ＞ 6.28立方米
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
3、长方体，正方体，圆柱体，圆锥的体积计算公式是 什么？它们是怎么推导出来的？
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
长方体的体积公式推导过程
4厘米
2 厘 米
3厘米
长方体的体积＝长×宽×高
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
正方体体积的推导过程
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
正方体的体积＝棱长×棱长×棱长
（× ）
5、正方体棱长扩大2倍，体积扩大8倍。
(√ )
在括号里填合适的单位
平方米
毫升
立方米
立方分米
升
灵活运用 你最棒！
联系生活
1、罐头四周商标纸是求（ 侧面积 ）. 2、制作通风管所需材料是求（ 侧面积 ）. 3、压路机压路面积是求（侧面积 ）. 4、油桶最多可贮存汽油多少升是求（ 容积 ）. 5、圆锥形沙堆占地面积指的是（底面积 ）. 6、游泳池的四周和底面贴瓷砖的面积是求 （ 侧面积+底面积 ）
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆锥体积的推导过程
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆锥的体积=底面积×高×
1 3
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆锥体积的推导过程
---------------
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
正方体体积的推导过程
因为正方体是 长、宽、高都 相等的长方体， 所以
棱长
棱长
棱长
正长方体的体积 ＝ 棱长长 × 棱宽长 ×棱高长
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
立体图形
长方体 正方体 圆柱体 圆锥
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
知识清单：
1、什么是立体图形的表面积？长方体、正方体、圆 柱的表面积各怎样计算？
2、什么是物体的体积？什么是容器的容积？ 3、长方体，正方体，圆柱体，圆锥的体积计算公式是 什么？它们是怎么推导出来的？
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
结论：圆柱体积是等底等
高 圆锥体积的3倍 ，圆锥
体积是等底等高圆柱体积
的 。13
圆锥的体积=底面积×高×
1 3
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
r h
底面 侧面
高
底面的周长
底面
圆柱的表面积=侧面积+底面积×2
底面周长×高
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
2、什么是物体的体积？什么是容器的容积？
物体所占空间的大小叫做物体的体积。 容器所能容纳物体的体积叫做物体的容积。
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
1、什么是立体图形的表面积？长方体、正方体、圆 柱的表面积各怎样计算？
一个立体图形所有的面的面积总和，叫做它的表面积。
h
a
b
左面
后面 下面 前面 上面
右面
长方体的表面积 =（长×宽+长×高+宽×高）×2
长方体的表面积 =长×宽×2 +长×高×2 +宽×高×2
a
正方体的表面积=棱长×棱长×6
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34 六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
拼成的长方体与原来的圆柱体 比较，什么变了？什么没变？
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34 六年级下册数学课件《6、立体图形的 表面积 和体积 1》苏 教版34
圆柱体积＝底面积× 高 长方体体积 ＝底面积 × 高