教程1如何进行常规坐标转换
- 格式:ppt
- 大小:4.20 MB
- 文档页数:1
坐标如何转换呢?1.我们打开CASS6.1的界面来,把在野外测的假设数据展上去,如图:2.找到在图中的假设任意两个控制点的坐标,如图:图中的D3和D4是我们假设的坐标控制点,为了方便更容易看到,我把它用线连起来了。
3.再把用GPS实测的坐标展上去,如图:图中的d3.2和d4.1就是控制点真实的D3和D4坐标,下一步就是如何把假设的D3和D4转换d3.2和d4.1真实的坐标。
请看以下操作:<步骤1>我们先把两个文件都展上去,如图:在图上我们可能看不清,但我们用两个“○”表示两个数据文件在CASS的界面上,下面我们请看具体的操作步骤:<步骤1>:在CASS界面中的菜单上点击“地物编辑”的“测站改正”<步骤2>:纠正前的第一点D3和第二点D4的方向<步骤3>:纠正后的第一点d3.2和纠正后的第二点方向d4.1<步骤4>:选择要纠正的实体图形<步骤5>:选好后按电脑键盘上回车键(Enter)。
则完成坐标转换。
<步骤6>:按回车键后它会自动跳出一个对话框“要输入纠正前的数据文件”<步骤7>:按打开它又会跳出对话框“输入纠正后数据文件名”按“保存“则完成坐标转换。
5.改高程的操作步骤:<步骤一>:在CASS界面中的菜单上点击“数据”的“批量修改坐标数据”<步骤二>:点击“批量修改坐标数据”则打开窗口:<步骤三>:填充里面的数据,点击原始数据文件名的“…”则打开窗口如下:<步骤四>选择“3.5下午坐标改正(已测完).dat”文件在打开<步骤五>点击打开后它又会跳出原来的窗口:再点击更改数据文件名的“…”则打开窗口:<步骤六>:在窗口中输入更改后的文件名“输入更改后数据文件名”<步骤七>:点击“保存”后又跳出原来的窗口<步骤八>:选择CASS系统默认的数据类型“处理所有数据”再输入“高程(H)”;高程是通过两个控制点的高程之差计算出来的,如:假设的(D3, 100.110 D4,100.242)高程和GPS实测的高程(d3.2, 266.069 d4.1, 266.112)之差,d3.2和D3之差为165.962,d4.1和D4之差为165.870,两个高程之差取平均为165.916。
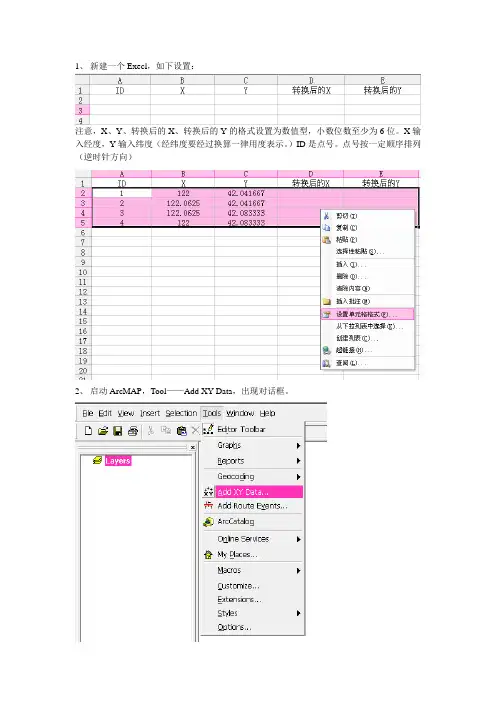
1、新建一个Execl,如下设置:注意,X、Y、转换后的X、转换后的Y的格式设置为数值型,小数位数至少为6位。
X输入经度,Y输入纬度(经纬度要经过换算一律用度表示。
)ID是点号。
点号按一定顺序排列(逆时针方向)2、启动ArcMAP,Tool——Add XY Data,出现对话框。
3、在对话框第一项里选择事先编辑好的Execl文件,观察X Filed和Y Filed 分别与Execl 里的X、Y对应。
4、点击“Edit”,选择“Select “,选择”Geographic Coordinate Systems “,——”Asia “。
根据图的左下角信息,判断是北京54还是西安80的坐标系,从而进行选择。
点击“确定“——”OK“——确定。
5、右击右面表格名称,选择“Label Feature “,点旁边注明点号,四个点就在绘图区站出来了。
6、点击右面工具条里的,双击点,可以查询点的准确坐标。
7、点击“View“里的”Data Frame Properties“,选择”Coordinate Systems“,选择”Predefined“里的”Projected Coordinate Systems “,再选择”Gauss Kruger“,根据图的左下角信息选择北京54或者西安80。
进入选项后,再根据图上格网横向坐标值前两位数字判断是40带还是41带(都是3度带),来进一步选择。
8、经过以上操作后,点的经纬度坐标已经转成以米为单位的坐标了。
利用查询工具,查出四个点的X、Y坐标,复制粘贴到第一步中建好的Execl中的“转换后的X、转换后的Y“里面,便于下一步在ERDAS中纠正。

坐标转换的方法坐标转换,这事儿听起来有点玄乎,但其实就像我们生活里换衣服一样。
比如说,你在自己家里穿着睡衣,自在又舒服,这就好比一种坐标体系下的状态。
可要是出门去参加个正式聚会呢,就得换上漂亮的礼服,这就相当于把你从家庭这个“坐标体系”转换到了社交聚会这个“坐标体系”。
在数学和地理等领域,坐标转换可是很实用的。
咱先说说平面坐标转换。
就像在一个大操场上,你可以用东西南北来描述自己的位置,这就是一种坐标表示。
可有时候呢,我们想要用另外一种方式来定位,比如说相对于某个建筑物的角度和距离。
这时候就需要转换坐标啦。
想象你在玩寻宝游戏,地图上给的是一种坐标,可你站在操场上看到的是周围的大树啊、球门啊这些实际的标志物,你就得把地图上的坐标转换成你眼睛看到的这种和实际标志物相关的坐标。
那怎么转呢?简单的平面坐标转换,就像是把一个拼图从横着放变成竖着放。
如果原来的坐标是(x,y),你要根据一定的规则,可能是旋转角度,可能是平移的距离,把它变成新的坐标(x',y')。
再说说空间坐标转换。
这就像是在一个大楼里找东西。
大楼有好多层,每一层又有好多房间。
你可以用楼层数、从某个起始点的横向距离、纵向距离来确定一个房间的位置,这是一种空间坐标。
但要是来了个新的管理方式,要用另外一套编号系统,这就需要进行坐标转换了。
比如说三维的直角坐标(x,y,z)要转换成球坐标(r,θ,φ)。
这就好比你本来是按照楼层、横向和纵向来描述房间位置,现在要变成按照离大楼中心的距离、仰角和方位角来描述。
这中间就涉及到一些复杂的数学关系。
但别怕,就像你学骑自行车,开始觉得难,摔几次就会了。
在地理上坐标转换也很常见。
我们都知道经纬度是描述地球上位置的坐标。
可是不同的地图投影方式,就需要不同的坐标转换。
比如说墨卡托投影下的坐标和高斯 - 克吕格投影下的坐标就不一样。
这就好比不同的画家画同一座山,一个从正面画,一个从侧面画,虽然画的是同一座山,但在画面上的表现形式就不一样。

坐标转换参数求取及坐标转换程序设计坐标转换是指将一个坐标系中的坐标点转换到另一个坐标系中的过程。
在实际应用中,常常需要将不同的坐标系之间进行转换,用于地图显示、位置定位等领域。
坐标转换参数是用来描述不同坐标系之间的变换关系的参数,一旦确定了转换参数,就可以通过程序进行坐标转换。
常见的坐标转换包括经纬度坐标与平面坐标之间的转换、不同坐标系统之间的转换等。
要确定坐标转换参数,一般需要进行以下几个步骤:1.收集待转换的坐标数据:收集需要转换的坐标点数据,包括原始坐标系和目标坐标系的坐标点。
2.确定转换方法:根据待转换的坐标数据,确定合适的转换方法。
常见的转换方法包括三参数转换、七参数转换等。
3.选择控制点:根据待转换的坐标数据,在原始坐标系和目标坐标系中选择一些已知的控制点,用于计算转换参数。
控制点一般应分布在地图上各个区域,并且坐标点的准确性要得到保证。
4.计算转换参数:利用所选控制点的坐标数据,根据转换方法进行计算,得到转换参数。
坐标转换程序设计主要包括以下几个步骤:1.定义数据结构:定义表示坐标点的数据结构,包括坐标系类型、坐标点的经纬度或平面坐标、转换参数等。
2.实现坐标转换函数:根据已知的转换方法,实现相应的坐标转换函数。
函数输入包括待转换的坐标点和转换参数,输出为转换后的坐标点。
3.实现转换参数计算函数:根据已知的控制点坐标数据,实现转换参数计算函数。
函数输入包括原始坐标系和目标坐标系中的控制点坐标,输出为计算得到的转换参数。
4.编写测试程序:编写测试程序,包括输入待转换的坐标点数据、转换参数等,调用坐标转换函数进行转换,并输出转换结果。
此外,还可以考虑使用现有的坐标转换库或API,如Proj4、GDAL等,以简化开发过程。
总之,坐标转换参数的求取和坐标转换程序设计是一个比较复杂的过程,需要针对具体应用场景进行细致的分析和设计。
通过合理选择转换方法和控制点,结合编写程序进行坐标转换,可以实现不同坐标系之间的精确转换。

如何进行测绘技术的地理坐标转换地理坐标转换是测绘技术中重要的环节之一。
在测绘过程中,我们常常需要将不同的坐标系之间进行转换,以便进行精确的测量和定位。
本文将探讨如何进行测绘技术的地理坐标转换,包括常见的坐标系、转换方法以及注意事项。
1. 常见的坐标系在测绘技术中,常见的坐标系有经纬度坐标系、高程坐标系、平面坐标系等。
经纬度坐标系是用来表示地球表面位置的一种坐标系,通过经度和纬度来确定一个点的位置。
高程坐标系是用来表示地球表面高度的坐标系,通常以海平面作为基准。
平面坐标系是将地球表面投影到一个平面上,以方便进行测绘和计算。
2. 坐标转换方法进行地理坐标转换的方法有很多种,常见的有大地坐标转换和平面坐标转换等。
2.1 大地坐标转换大地坐标转换主要是将经纬度坐标转换为其他坐标系,或者将其他坐标系转换为经纬度坐标。
其中最常用的转换方法是大地测量学中的大地坐标转换。
这种方法通过测量大地线的长度和方位角来确定两个点之间的距离和方向,从而实现坐标系之间的转换。
2.2 平面坐标转换平面坐标转换主要是将不同平面坐标系之间进行转换。
常见的平面坐标系有UTM坐标系、高斯-克吕格坐标系等。
转换方法包括坐标轴平移、旋转、尺度变换以及仿射变换等。
其中,仿射变换是一种常用的转换方法,它通过将原坐标系中的坐标点映射到目标坐标系中,实现坐标转换。
3. 注意事项在进行地理坐标转换时,需要注意一些问题,以确保转换的准确性和可靠性。
3.1 坐标系选择在进行坐标转换前,需要先确定所采用的坐标系。
不同的测绘任务和应用场景可能需要采用不同的坐标系,需根据具体情况进行选择。
3.2 参数设置转换过程中需要设置一些参数,如椭球参数、投影参数等。
这些参数的准确性对于转换结果的精度至关重要,需要根据实际情况进行合理设置。
3.3 数据质量进行坐标转换时,需要保证原始坐标数据的质量。
对于已有的坐标数据,需要检查其精度和完整性,以避免错误转换或者不必要的误差。

经纬度转西安80坐标系坐标转换方法一、分带划分1.我国采用6度分带和3度分带:1∶2.5万及1∶5万的地形图采用6度分带投影,即经差为6度,从零度子午线开始,自西向东每个经差6度为一投影带,全球共分60个带,用1,2,3,4,5,……表示.即东经0~6度为第一带,其中央经线的经度为东经3度,东经6~12度为第二带,其中央经线的经度为9度。
1∶1万的地形图采用3度分带,从东经1.5度的经线开始,每隔3度为一带,用1,2,3,……表示,全球共划分120个投影带,即东经1.5~ 4.5度为第1带,其中央经线的经度为东经3度,东经4.5~7.5度为第2带,其中央经线的经度为东经6度.我省位于东经113度-东经120度之间,跨第38、39、40共计3个带,其中东经115.5度以西为第38带,其中央经线为东经114度;东经115.5~118.5度为39带,其中央经线为东经117度;东经118.5度以东到山海关为40带,其中央经线为东经120度。
地形图上公里网横坐标前2位就是带号,例如:1∶5万地形图上的横坐标为,其中20即为带号,345486为横坐标值。
2.当地中央经线经度的计算六度带中央经线经度的计算:当地中央经线经度=6°×当地带号-3°,例如:地形图上的横坐标为20345,其所处的六度带的中央经线经度为:6°×20-3°=117°(适用于1∶2.5万和1∶5万地形图)。
三度带中央经线经度的计算:中央经线经度=3°×当地带号(适用于1∶1万地形图)。
3、如何计算当地的中央子午线?当地中央子午线决定于当地的直角坐标系统,首先确定您的直角坐标系统是3度带还是6度带投影公式推算:6度带中央子午线计算公式:当地经度/6=N;中央子午线L=6 * N (带号)当没有除尽,N有余数时,中央子午线L=6*N - 33度带中央子午线计算公式:当地经度/3=N;中央子午线L=3 X N我国的经度范围西起73°东至135°,可分成六度带十一个(13号带—23号带),各带中央经线依次为(75°、81°、 (1)23°、129°、135°);三度带二十二个(24号带—45号带)。

如何使用测绘软件进行坐标转换与投影变换坐标转换和投影变换在测绘工作中是非常重要的一部分。
使用测绘软件进行坐标转换和投影变换可以提高测量精度,并且方便了测绘工作者的工作。
本文将介绍如何使用测绘软件进行坐标转换和投影变换。
在测绘工作中,我们经常会遇到不同坐标系下的坐标点。
要进行坐标转换,我们需要知道两个坐标系之间的转换参数。
在测绘软件中,通常会提供一些常用的坐标系的转换参数,比如WGS84和北京54之间的转换参数。
如果需要转换的坐标系不在软件中提供的参数中,我们需要手动输入转换参数。
首先,我们需要在测绘软件中导入待转换的坐标数据。
一般情况下,坐标数据以文本文件的形式存在,比如CSV文件。
我们可以使用软件提供的导入功能,将文件导入到软件中。
在导入坐标数据后,我们需要选择进行的坐标转换操作。
常见的坐标转换操作包括坐标系转换、坐标点加密、坐标点解密等。
选择适当的操作后,软件会根据提供的参数进行坐标转换。
在转换完成后,我们可以将转换后的坐标数据导出到文件,以进行后续的使用或分析。
除了坐标转换,投影变换也是测绘工作中常用的操作。
投影变换是将三维地理空间对象映射到二维平面上的过程。
在投影变换过程中,我们需要选择合适的投影方式,并提供相应的参数。
不同的地理区域和精度要求可能需要不同的投影方式,比如墨卡托投影、兰勃特投影、高斯投影等。
在选择投影方式时,我们需要考虑到地理区域的形状、大小和所需的精度等因素。
在进行投影变换时,我们可以选择将所有对象进行投影,也可以选择只对部分对象进行投影。
通常情况下,我们会选择将整个地理区域进行投影,以保证地理空间对象的完整性。
在投影完成后,我们可以对投影后的数据进行编辑和分析,以满足各种测绘需求。
在使用测绘软件进行坐标转换和投影变换时,我们需要注意一些常见的问题。
首先,我们需要确保输入的坐标数据符合要求,比如坐标值的格式和坐标系的一致性。
其次,我们需要对输入的参数进行检查,以避免参数错误导致的转换错误。

坐标转换最简单方法坐标转换是一种将一个坐标系中的点转换到另一个坐标系中的点的方法。
在现代科技中,坐标转换是非常重要的,因为它可以帮助我们在不同的坐标系中进行数据分析和处理。
在本文中,我们将介绍最简单的坐标转换方法。
我们需要了解两个坐标系之间的关系。
通常情况下,我们使用笛卡尔坐标系来表示二维平面上的点。
笛卡尔坐标系由两条互相垂直的轴组成,分别称为x轴和y轴。
在这个坐标系中,每个点都可以用一个有序对(x,y)来表示。
另一方面,地理坐标系是用来表示地球表面上的点的。
地球是一个球体,因此地理坐标系需要使用经度和纬度来表示一个点的位置。
经度是指一个点相对于本初子午线的角度,而纬度是指一个点相对于赤道的角度。
现在,我们来介绍最简单的坐标转换方法。
假设我们有一个点在笛卡尔坐标系中的坐标为(x,y),我们想要将它转换到地理坐标系中。
我们可以按照以下步骤进行转换:1. 确定地球的半径。
地球的半径约为6371公里。
2. 将笛卡尔坐标系中的x和y值转换为以地球中心为原点的三维坐标系中的x、y和z值。
具体方法是:x = x * cos(y) * cos(x)y = x * cos(y) * sin(x)z = y * sin(y)3. 计算该点相对于地球中心的距离。
具体方法是:distance = sqrt(x^2 + y^2 + z^2)4. 计算该点相对于本初子午线的经度。
具体方法是:longitude = atan2(y, x)5. 计算该点相对于赤道的纬度。
具体方法是:latitude = asin(z / distance)6. 将经度和纬度转换为度数。
具体方法是:longitude = longitude * 180 / pilatitude = latitude * 180 / pi7. 最后,我们得到了该点在地理坐标系中的坐标,即(longitude, latitude)。
以上就是最简单的坐标转换方法。

三鼎RTK一T3坐标转换一、四参数示例:2000坐标系转地方坐标系准备材料:2个以上的已知点坐标步骤:1.打开求转换参数操作:“输入”→“求转换参数”2.设置四参数在求转换参数界面首先点击右上角的设置按钮,将“坐标转换方法”改为“一步法”,点击“确定”,则可以开始四参数的设置。
3.添加坐标参数“一步法”设置完成后,在求转换参数界面点击“添加”4.输入坐标参数平面坐标输入已知点坐标,大地坐标输入RTK测的已知点的坐标。
大地坐标可以点击更多获取方式,里面有“定位获取”和“点库获取”,输入完成以后,点击“确定”,添加完第一个坐标Pt1。
然后以同样的方法输入第二个坐标Pt25.计算四参数并应用如果Pt1或Pt2不小心输入错误,单击改点可进行编辑或者删除。
坐标输入无误后,点击“计算”即可获得2000坐标系转当地坐标系的四参数,再点击“应用”即可,再进行点测量时,获取的坐标就是当地坐标系了。
需要主要的是,四参数覆盖范围较少,一般推荐使用七参数。
二、七参数示例说明:2000坐标系转地方坐标系准备材料:3个以上的已知点坐标1.打开求转换参数操作:“输入”→“求转换参数”2.设置七参数在求转换参数界面首先点击右上角的设置按钮,将“坐标转换方法”改为“七参数”,点击“确定”,则可以开始七参数的设置。
3.添加坐标参数“七参数”设置完成后,在求转换参数界面点击“添加”4.输入坐标参数坐标输入方法同四参数一样,但是需要至少输入3个已知点坐标。
输入完成后点击“计算”即可获得2000坐标系转当地坐标系的七参数,最后点击应用即可。


坐标转换步骤1、总平图找个已知的点的坐标2、首先用快捷键D调出标注样式3、把精度调成0.00000000000测量这个点的角度4、因为总平图都是倾斜的和正交的情况下有一定的角度5、把单项的图纸打开6、全部框选7、右键旋转8、输入总平图的角度9、然后enter确认10、从总平图中记录交点的坐标11、在单项图纸中usc命令----N命定----鼠标左键点击交点,此时此交点已被定义为0点12、输入zbbz命令----点击交点-----显示坐标为 0,0,013、再次ucs命令---鼠标左键移动到交点位置(切记不要点击)-----此时输入坐标值14、输入坐标的方法为------先输入Y坐标(坐标值前输入负号)-----输入标点“,”---------------再输入X坐标(坐标值前输入负号)-----输入标点“,”-----------------再输入Z坐标(一般都为0)15、连续点击两次enter键,此时此交点已被定义为输入的坐标值16、再次zbbz命令----此时会显示和从总平图中记录交点的坐标一致17、大功告成截图如下1、打开总平图,总平图找个已知的点的坐标2、快捷键D----ENter---如下3、点击修改,调节右下角精度为最大4、点击置为当前,点击关闭5、点击标注----角度6、打开单项图纸如下7、全部框选-------右键旋转-----点击交点8、输入角度9、enter确定10、ucs命令----输入N11、enter确定-----点击交点12、输入zbbz命令13、enter确定14、再次ucs命令15、enter确定-----输入坐标16、鼠标十字丝移动到交点位置(切勿点击)---连续点击两次enter键17、输入zbbz命令18、enter确定大功告成。
测量坐标转换的方法与注意事项作为现代测量技术中的重要环节,坐标转换是将测量点的局部坐标转化为全局坐标的过程。
在工程测绘、地理空间信息系统等领域中,坐标转换的准确性和可靠性对于数据的分析和应用是至关重要的。
本文将介绍一些常用的坐标转换方法,并探讨在实际应用中需要注意的问题。
一、坐标转换方法1. 基本的坐标转换方法常见的坐标转换方法有参数法、公式法和点位校正法。
参数法是通过计算坐标转换的七参数或三参数,通过线性变换将局部坐标转换为全局坐标。
公式法根据坐标系之间的数学关系推导坐标转换的公式,通过运算将局部坐标转换为全局坐标。
点位校正法是通过测量已知控制点的坐标,并与已知全局坐标进行比较,通过求解得到转换参数,再将局部坐标转换为全局坐标。
2. 常用的坐标转换软件目前,有许多软件可用于坐标转换,如AutoCAD、ArcGIS等。
这些软件提供了丰富的功能和工具,可以方便地进行坐标转换。
同时,它们还支持各种坐标系统和转换方法,用户可以根据自己的需求选择合适的软件进行坐标转换操作。
二、坐标转换注意事项1. 坐标系统的选择在进行坐标转换之前,需要明确所使用的坐标系统。
不同的工程和应用场景可能使用不同的坐标系统,如地理坐标系统、测量坐标系统等。
在选择坐标系统时,需要考虑到数据的准确性和使用的便利性,确保所选择的坐标系统与实际情况相符。
2. 坐标转换精度的控制坐标转换的精度对于数据的可信度和应用的有效性至关重要。
在进行坐标转换时,需要根据具体的要求和使用场景制定相应的精度要求。
一般来说,控制点的选取和精确测量是保证精度的关键。
另外,坐标转换过程中的误差传递也需要考虑,尽可能减小误差的累积和传递,以提高转换的准确性。
3. 转换参数的确定在使用参数法进行坐标转换时,参数的确定对于转换结果的准确性有着重要影响。
参数的选取应综合考虑控制点的数量和分布,同时还需要考虑控制点的测量精度和数据的质量。
通常情况下,参数的确定需要进行精确的计算和模拟实验,以确保转换的准确性。
一、COORD软件批量转换(平面坐标转为经纬度)
二、坐标换带(同一坐标下下3度带转为6度带等)
(万能坐标转换软件也可以:打开软件后点击“工具”—“坐标换带”,之后如下图
打开软件后,“设置”--“地形投影”—设置是属于3度带还是6度带,输入中央经度,
四、坐标系间的转换
设置四参数后就可以转换了
可以“文件转换”进行批量处理
五、WGS84转成地方坐标系
步骤:
1.1.新建坐标转换文件,便于下次使用转换是不用重新输入,直接打开即可。
2.2.设置投影参数。
3.3.用一个已知点(WGS84坐标和北京54坐标),计算不同椭球转换的三参数(或七参数)。
4.4.确定转换参数。
5.5.打开七参数转换,完成WGS84到北京54的转换。
6.6.利用多个已知点(北京54坐标和佛山坐标),计算同一个椭球的地方坐标转换(四参数)。
7.7.确定转换参数
8.8.同时打开七参数和四参数。
完成WGS-84到佛山坐标的转换。
标准实用文案大全。
如何进行坐标转换与坐标系的选择在日常生活中,我们经常需要进行坐标转换与坐标系的选择,特别是在导航、地图和测绘等领域。
坐标转换是指将一个位置的坐标从一个坐标系转换到另一个坐标系,而坐标系的选择则决定了坐标转换的准确性和适用性。
本文将探讨如何进行坐标转换和坐标系的选择,以帮助读者更好地理解和应用这些概念。
首先,我们需要了解坐标转换的基本原理。
坐标转换通常涉及到两个坐标系,分别为源坐标系和目标坐标系。
源坐标系是我们要进行转换的坐标系,而目标坐标系是我们要将坐标转换成的坐标系。
常见的源坐标系包括经纬度坐标系、平面直角坐标系和高程坐标系,而目标坐标系则根据具体需求而定。
进行坐标转换的目的是为了在不同的坐标系下准确表示地球上的位置。
在进行坐标转换时,我们经常会用到大地模型和投影模型。
大地模型是用来描述地球形状的数学模型,其中最常用的是椭球体模型和球面模型。
椭球体模型适用于较大范围的地理坐标转换,如全球范围的经纬度转换。
而球面模型适用于较小范围的地理坐标转换,如城市地图的转换。
投影模型则是将三维地球表面映射到二维平面上的数学模型,以解决地球表面的变形问题。
常见的投影模型包括等距圆柱投影、墨卡托投影和兰伯特投影等。
在选择坐标系时,应根据具体的应用需求来判断。
例如,如果我们需要进行导航和路径规划,常见的选择是使用平面直角坐标系,以便更精确地表示位置和方向。
而在测绘和地图制作领域,通常会选择投影坐标系,以解决地球表面的变形问题。
此外,不同的国家和地区也会使用自己独特的坐标系,如中国采用的“2000国家大地坐标系”。
进行坐标转换时,我们可以借助专业的地理信息系统(GIS)软件或在线地图服务来实现。
这些工具通常提供了多种坐标转换方法和坐标系的选择,使我们在实际操作中更加方便和准确。
在使用这些工具时,我们需要输入源坐标系和目标坐标系的参数,如大地模型和投影模型的参数,以进行精确的坐标转换。
此外,坐标转换过程中还需要考虑精度和误差问题。
利用COORD进行坐标系转换教程一、COORD软件介绍COORD 4.1坐标转换软件(其它版本可能有问题),是一个免费的坐标转换软件,也是测绘人常备的一个工具之一。
在下边的时间里,就给大家演示一下该软件在通过三个以上已知点计算七参数时的一些操作。
图1:软件界面二.COORD实例1.转换原理国家80坐标系(又叫西安80坐标系)与北京54坐标系其实是一种椭球参数的转换,作为这种转换在同一个椭球里的转换都是严密的,而在不同的椭球之间的转换是不严密,因此不存在一套转换参数可以全国通用的,在每个地方会不一样,因为它们是两个不同的椭球基准。
那么,两个椭球间的坐标转换,一般而言比较严密的是用七参数布尔莎模型,即 X 平移, Y 平移, Z 平移, X 旋转(WX), Y 旋转(WY), Z 旋转(WZ),尺度变化(DM )。
要求得七参数就需要在一个地区需要 3 个以上的已知点。
如果区域范围不大,最远点间的距离不大于 30Km(经验值),这可以用三参数,即 X 平移,Y 平移, Z 平移,而将 X 旋转, Y 旋转, Z 旋转,尺度变化面DM视为 01.1 两坐标系公共点坐标数据表1:示例数据1.2 投影参数投影方式:高斯-克吕格3度带;中央子午线:117度2.计算七参数2.1 求北京54 坐标系--> 国家80坐标系的七参数根据两个已有坐标(例3个)求七参数;在操作之前必须先将中央子午线必须先输好;图2:投影参数设置输入两个坐标系三个或三个以上相对应的坐标,输入完后点击“计算”可以看到其中的点位精度,当点击“确定”时,软件将自动将七参数设置好。
图3:已知数据的输入注意:请注意椭球的选择顺序,如果我们要计算北京54->国家80,在这里源坐标应该是国家80坐标系,反之亦反。
接下来就是选中“七参数转换”,设定转换坐标系。
可以查看输出的值,这个值一定就是我们所需的,我们可以返回我的刚计算的七参数,看是否正确。
坐标系的转换方法我折腾了好久坐标系的转换方法,总算找到点门道。
说实话,坐标系转换这事,我一开始也是瞎摸索。
我就知道在平面直角坐标系里,坐标就是个横竖的位置表示。
咱先拿笛卡尔坐标系,也就是常见的直角坐标系来说吧。
我最早是研究在平移的情况下怎么转换坐标。
我想啊,这就像你在一个方格纸上移动物体一样。
假如你有个点,原本的坐标是(x,y)。
如果沿着x轴正方向平移了a个单位,沿着y轴正方向平移了b个单位,那新坐标不就成了(x + a,y + b)嘛。
这就好比你把东西从家里的一个角落移到另一个角落,相对的坐标位置就变了。
但是后来遇到旋转的情况就把我难住了。
我试了好多次,乱算一通。
我之前想着按照角度就直接加减数值,结果发现完全不对。
后来我认真查了资料才知道,假如绕原点旋转,旋转角度是θ的话,这时候坐标转换就得用三角函数了。
对于原来的点(x,y),新坐标的x'就等于x乘以cosθ减去y乘以sinθ,y'就等于x乘以sinθ加上y乘以cosθ。
这可把我绕晕了好一阵呢,就像在迷宫里转圈圈。
还有从平面直角坐标系转换到极坐标系的情况。
这个我一开始也是摸不着头脑。
我就知道极坐标系是用距离和角度来表示一个点。
我尝试着拿几个简单的点去做转换,比如直角坐标系里的(1,1)这个点。
我慢慢琢磨,发现先得求这个点到原点的距离,根据勾股定理,这个距离r就等于根号下(x平方+y平方),这里x和y就是直角坐标系里的坐标值嘛,那r就是根号2啦。
然后角度呢,得看看这个点在第几象限。
对于(1,1)这个点,角度θ就是45度或者说π/4弧度。
但这里开始的时候我就容易把角度的范围搞错,有时候算出来的角度不是正确的范围里的。
我意识到一定要根据x 和y的正负确定好角度所在象限。
三维坐标系转换就更麻烦了。
我感觉自己像是走进了一团迷雾里。
我试了一些计算方法,就像平移,就像在长宽高都能移动的大箱子里移动物品一样,在各个轴上做加减。
但是对于旋转,那就复杂得不得了,涉及到好多矩阵运算。