计算星期几
- 格式:doc
- 大小:62.50 KB
- 文档页数:3

计算某天是星期几(含六个例程)计算某天是星期几,最常见的公式: W = [Y-1] + [(Y-1)/4] - [(Y-1)/100] + [(Y-1)/400] + D Y是年份数,D是这一天在这一年中的累积天数,也就是这一天在这一年中是第几天。
计算某天是星期几,最常见的公式:W=[Y-1]+[(Y-1)/4]-[(Y-1)/100]+[(Y-1)/400]+DY是年份数,D是这一天在这一年中的累积天数,也就是这一天在这一年中是第几天。
最好用的是蔡勒公式:W=[C/4]-2C+y+[y/4]+[13*(M+1)/5]+d-1C是世纪数减一,y是年份后两位,M是月份,d是日数。
1月和2月要按上一年的13月和14月来算,这时C和y均按上一年取值。
两个公式中的[...]均指只取计算结果的整数部分。
算出来的W除以7,余数是几就是星期几。
如果余数是0,则为星期日。
星期制度是一种有古老传统的制度。
据说因为《圣经〃创世纪》中规定上帝用了六天时间创世纪,第七天休息,所以人们也就以七天为一个周期来安排自己的工作和生活,而星期日是休息日。
从实际的角度来讲,以七天为一个周期,长短也比较合适。
所以尽管中国的传统工作周期是十天(比如王勃《滕王阁序》中说的“十旬休暇”,即是指官员的工作每十日为一个周期,第十日休假),但后来也采取了西方的星期制度。
在日常生活中,我们常常遇到要知道某一天是星期几的问题。
有时候,我们还想知道历史上某一天是星期几。
通常,解决这个方法的有效办法是看日历,但是我们总不会随时随身带着日历,更不可能随时随身带着几千年的万年历。
假如是想在计算机编程中计算某一天是星期几,预先把一本万年历存进去就更不现实了。
这时候是不是有办法通过什么公式,从年月日推出这一天是星期几呢?答案是肯定的。
其实我们也常常在这样做。
我们先举一个简单的例子。
比如,知道了2004年5月1日是星期六,那么2004年5月31日“世界无烟日”是星期几就不难推算出来。

计算星期几的方法计算任何一个日期是星期几的方法蔡勒公式W = [C/4] - 2C + y + [y/4] + [13 X(M+1) / 5] + d - 1 C是世纪数减1 , y是年份后两位,M是月份(从3月开始,1月和2月要按上一年的13月和14月来算,这时C和y 均按上一年取值),d 是日数。
求出W的值,再除以7,余几就是星期几,余数为0,则是星期天。
注意:[…]表示只取整数部分注意:公式中如计算得出负数,不能按习惯的余数的概念求余数,只能按数论中的余数的定义求余。
为了方便计算,我们可以给它加上一个7的整数倍,使它变为一个正数,比如加上7、14、21、28等,得到一个整数后,再除以7,余几,说明这一天是星期几。
例1 : 2004年的9月1日是星期几?C=20 y=04 M=9 d=1W = [C/4] - 2C + y + [y/4] + [13 x(M+1) / 5] + d - 1 =[20/4] - 2 X20 + 04 + [04/4] + [13 X(9 + 1 ) /5] + 1=5 - 40 + 4 + 1 + [13 X2] + 1 - 1=5 - 40 + 4 + 1 + 26 + 1 - 1=—4W为负数不行,加7的倍数14,得10。
10除以7,余数为3 , 2004年的9月1日是星期三。
例2 : 2010年的7月15日是星期几?C=20 y=10 M=7 d=15W = [C/4] - 2C + y + [y/4] + [13 x(M+1) / 5] + d - 1 =[20/4] — 2 X20 + 10 + [10/4] + [13 X(7 + 1 ) /5] + 15 —1=5 —40 + 10 + 2 + [13 X8/5] + 14=—23 + 20 + 14=1111除以7余数为4, 2010年的7月15日是星期四。
链接:1世纪为100年2000年以后为21世纪,以此类推1个年代为10年90-99为90年代,以此类推!女口:1900年是19世纪、1901年是20世纪、2000年是20世纪、2001年是21世纪。

星期数的计算懂得公历日期变化规律的人都可以将一个日期的星期数计算出来,如果不知道正确的方法可能会很是麻烦。
现在我们给出一个方便的计算星期数的公式,为此首先规定:星期日=0,星期一=1,星期二=2,星期三=3,星期四=4,星期五=5,星期六=6另外注意闰年比平年多加的一天不是年头也不是年尾,而是在2月29日,所以为了计算方便,我们把3月作为一年的第一个月,4月作为一年的第二个月……而1月、2月则分别为去年的第十一个月和第十二个月。
作了这样的规定之后,1997年7月1日就要写为1997年“5月”1日,2000年1月2日就要写为1999年“11月”2日。
现在假定给出一个日期:N年m月d日(年份N=100c+y,其中c为世纪数,y为年代数),则该日期的星期数W=d+[ (13m-1)]+y+[ y]+[ c]-2c(mod7)其中方括号表示不超过这个数的最大整数,mod为数学符号,如a(modb)表示一个数,此数在0到b范围内(若b小于零,则在b到0范围内),若a∈[0,b),则a(modb) =a,若a不在0到b范围内,则a(modb)等于a加或减b的整数倍后处于0到b范围内的一个值。
这里值得注意的是,目前国际通用的公历是教皇格里高利十三实行的。
当时他召集了很多学者和僧侣讨论历法改革问题,决定采用业余天文学家利里奥的方案,没四百年去掉三个闰日。
公元1582年格里高利颁发改历的命令:(1)把1582年10月4日后的一天改为1582年10月25日;(2)那些世纪数不能被4整除的世纪年,如1700、1800、1900、2100、……不再作为闰年,仍算为平年。
这两条规定至为重要,第一条规定实质上把春分固定在3月21日左右,解决了日历与天时不符合的矛盾,第二条规定使历法的精度大大提高,保证了这种历法在相当长的时间里仍能实用。
根据这项规定,每400年中有97个闰年,总天数为365×400+97=146097(天)因此平均每年的长度为146097÷400=365.2425(天)这与回归年实际值365.2422天相差仅有0.0003天,换句话说,要经过3300多年,两者才有一天的相差。

知道公历日期计算星期:
黄远珦
随便给一个日期,就可以推算出是星期几。
计算方法如下:模拟数除以7的余数就是星期数(星期几) 模拟数= [世纪/4] - 2乘以世纪+ 年份+ [年份除以4] + [13 乘以(月份+1) / 5] + 当月天数- 1 可以用公示来表示; Q = [S/4] - 2S + N + [N/4] + [13 * (y+1) / 5] + t - 1 公式中的符号含义如下: Q:星期;(Q对7取模得:0-星期日,1-星期一,2-星期二,3-星期三,4-星期四,5-星期五,6-星期六)S:世纪(前两位数)N:年(后两位数)y:月(y大于等于3,小于等于14,即在本公式中,某年的1、2月要看作上一年的13、14月来计算,比如2018年1月1日要看作2017年的13月1日来计算)t:日[ ]代表取整,即只要整数部分。

口算星期几只要记住12个系数就行,这12个系数就是12个月的一号是星期几,再减1。
如7月1日是星期天,系数就是7-1=6,2月1日是星期四,系数就是3,口算时只要用该日期加该月系数,再除以7,如能整除,这一天就是星期天;如不能整除,余数是几就是星期几。
道理很简单,12个系数是必背的,当然每年都不同,就当是手机号码应该很容易背,背一次用一年,很值~在朋友面前露一手,说不定他们还称奇。
网上搜的,供参考。
历史上的某一天是星期几,未来的某一天是星期几,关于这个问题有这样的一种算法介绍如下:某年某月某日是星期几的推算公式:〔(χ,1),“(χ,1)/4”,“(χ,1)/100”,“(χ,1)/400”,y〕?7这个公式中的χ表示那一年的公历年份数,y表示某日在那一年的第几天,“”表示整数商。
计算所得的余数就是星期几(余数为0则是星期日)。
例1、 1980年6月1日是星期几,分析:χ,1,1980,1=1979,“(χ,1)/4”,494,“(χ,1)/100”,19,“(χ,1)/400”,4;y,31,29,31,30,31,1,153(天)。
解:(1979,494,19,4,153)?7,2611?7,373(余数为0)。
所以,1980年6月1日是星期日。
一、年码的计算(1)21世纪年码算法:mod(X+int(X/4),7)(X代表年份的后三位数字,如:2015年,这里X就代表15,int代表向下取整,mod代表取余)(2)其它世纪的年码算法:20世纪年码=21世纪年码+1,即 mod(X+int(X/4),7)+119世纪年码=21世纪年码+3,即 mod(X+int(X/4),7)+318世纪年码=22世纪年码=21世纪年码+5(或减2),即mod(X+int(X/4),7)+5二、牢记月码(1)任何世纪中的任何年份对应的月码都是相同的,十二个月分别对应的月码是:51(26)2503514624(括号内的数字代表闰年时1月、2月的月码)记忆方法:平年1、4、7月为5;2、8月为1;3、11月为2;5月为0;6月为3;9、12月为4;10月为6。

星期几的速算方法五篇范文第一篇:星期几的速算方法在学习了找规律以后,经常会出现一些求“某月某日”是星期几的问题。
例如:“今年一月一日是星期五,十月一日是星期几?”解这道题的一般方法是:(1)先求出一月一日到十月一日的天数和31+28+31+30+31+30+31+31+30+1=274(天)(2)再求出7除天数和的余数274÷7=39(组)……1(天)(3)最后求出十月一日是星期几从星期五算起,因余数是1,所以十月一日是星期五。
这种算法在求“天数和”及“余数”时,既麻烦又容易出错。
有一种求星期网几的简便速算法——“7余数”法。
“7余数”法是指一个数除以7,得到的余数。
(若一个数能被7除尽,余数为0。
)每年各月份按天数多少分组,分别列出它们的7余数如下:大月(31天的有:1月、3月、5月、7月、8月、10月、12月)的7余数是3。
小月(30天的有:4月、6月、9月、11月)的7余数是2。
平年二月(28天)的7余数是0。
闰年二月(29天)的7余数是1。
这样前面的题共经过五个大月三个小月和一个平月,再加网上十月一日这一天,共经过天数的7余数为:3×5+2×3+0+1=22(天),22的7余数是1。
所以今年十月一日与元旦同是星期五。
第二篇:16年教师节是哪一天?星期几?2016年教师节是哪一天?星期几?问:2016年教师节是哪一天?星期几?答:2016年教师节是2016年9月10日农历八月十七星期三中国教师节中国有悠久的尊师重道的传统,古代就有“人有三尊,君、父、师”的说法。
《吕氏春秋·尊师》云:“生则谨养,死则敬祭,此尊师之道也。
”《师说》中:“师者,所以传道授业解惑也。
”在中国几千年的灿烂历史中,“师”,总是受人尊敬,被人爱戴的。
老师,是人类文化得以传承的功臣,他们做的贡献是极其巨大的。
教师节的宗旨就是提高人们对教师为教育事业所做贡献的认识和评价。
1931年,教育家邰爽秋、程其保等在南京中央大学集会,发表要求“改善教师待遇,保障教师工作和增进教师修养”的宣言,并议定6月6日为教师节,也称双六节。
星期几的速算方法!
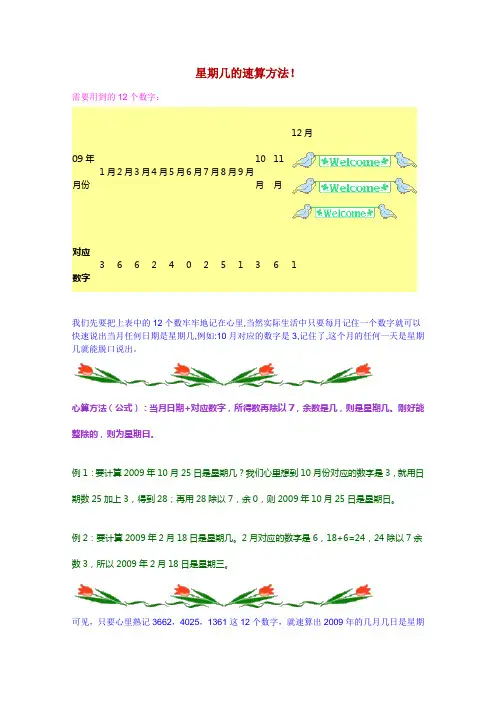
需要用到的12个数字:
我们先要把上表中的12个数牢牢地记在心里,当然实际生活中只要每月记住一个数字就可以快速说出当月任何日期是星期几,例如:10月对应的数字是3,记住了,这个月的任何一天是星期几就能脱口说出。
心算方法(公式):当月日期+对应数字,所得数再除以7,余数是几,则是星期几。
刚好能整除的,则为星期日。
例1:要计算2009年10月25日是星期几?我们心里想到10月份对应的数字是3,就用日期数25加上3,得到28;再用28除以7,余0,则2009年10月25日是星期日。
例2:要计算2009年2月18日是星期几。
2月对应的数字是6,18+6=24,24除以7余数3,所以2009年2月18日是星期三。
可见,只要心里熟记3662,4025,1361这12个数字,就速算出2009年的几月几日是星期几,是不是很酷?
那么3662,4025,1361这12个数字是从哪儿来的呢?它们就是分别所对应的月份的上一个月的最后一天的星期数。
例如,2009年9月30日是星期三,所以2009年10月份对应的数字就是3。
特别注意一下:2009年1月对应的数字,得去查2008年12月31日是星期几,用万年表容易查得是星期三,所以2009年1月对应的数字就是3。
以下是我用万年表查得2010-2012年各月所对应的数字,其他年份大家自已需要时再查。
1月2月3月4月5月6月7月8月9月10月11月12月
2010年400351362402 2011年511462403513
2012年62361462503
5
万年历。

计算星期几的常用公式
S =x -1+[41-x ]-[1001-x ]+[400
1-x ]+c 其中x 是公元的年数,c 是从这一年的元旦算起到这一天为止〔包括这一天在内〕的天数,方括号表示其中算式的整数部分,即在计算S 的值时,3个方括号中只要算出商数的整数部分,把余数略去不计、
按此算式求出的值后,除以7,余几确实是星期几,除尽了确实是星期日、 例1:西安事变发生在1936年12月12日,试计算当天是星期几? 解:x =1936,c =347
因此可得,
S =1936-1+[411936-]-[10011936-]+[400
11936-]+347 =1935+483-19+4+347
=2750
2750÷7=392 (6)
因此,西安事变发生在星期六、
例2:试计算1998年圣诞节是星期几?
解:圣诞节是12月25日,因此,x =1998,c =359
S =1998-1+[411998-]-[10011998-]+[400
11998-]+359 =1997+499-19+4+359
=2840
2840÷7=405 (5)
因此,1998年圣诞节是星期五、
那个计算方法依照的是每四年一闰、百年不闰、四百年再闰的历法,即格里历、格里历是从公元1582年开始实行的、因此,用那个方法能够计算公元1582年以后某年某月某日是星期几、。

根据年月日推算是星期几的公式有时候,想知道公元某年某月某日是星期几,可以用下面的公式算出来:这里的方括号表示只取商的整数部分。
式中:x :这一年是公元多少年。
y :这一天是这一年的第几天。
s :星期几。
不过要先除以7,再取余数。
没有余数是星期日,余数是1、2、3、4、5、6,分别是星期一、星期二、星期三、星期四、星期五、星期六。
比如,2010年国庆节(10月1日)是星期几?x =2010。
y =31+28+31+30+31+30+31+31+30+1=31×5+30×3+28+1=274。
s =2010-1+502-20+5+274=2770,2770÷7余5。
所以,2010年国庆节是星期五。
如果,你只想知道这个公式怎样用,到这儿就可以了。
而要想知道这个公式的道理是什么,那可就说来话长了。
“星期制”是公元321年3月7日,古罗马皇帝君士坦丁宣布开始实行的,并且规定这一天为星期一。
实际上,就是把公元元年元旦(公元1年1月1日)规定为星期一。
(相当于公式中的x =1,y =1,所以s =1。
)通常1年有365天,365÷7=52……1,就是说比52个星期多1天。
所以,同一个日期,下一年是星期几,就要比上一年向后推1天。
比如,上一年元旦是星期三,下一年元旦就是星期四。
“通常每过1年,把同一日期是星期几向后推1天”,是理解这个公式的关键。
要想知道某年某月某日是星期几,首先,要知道这一年元旦以公元元年元旦是星期一为起点,已经把星期几向后推了多少天,还要知道这一天是这一年的第几天。
而要知道这一年元旦已经把星期几向后推了多少天,可以从公元元年到这一年已经过了多少年算起,先按1年向后推1天计算,再根据闰年的规定进行调整。
闰年的规定是:年份是4的倍数的一般都是闰年,其中,年份是整百数的y x x x x s +⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡-+-=40011001411一般不是闰年,只有年份是400的倍数的才是闰年。

四种周几(星期几)推算法孙致平编辑一、周数法(主要用周数推算,最易理解的法)举例说明。
题:算2019年10月1日周几。
解:该日公元总天数=》离该日当年且小于当年的闰年数/4*1461+平年数*365+零天数=》2016/4*1461+2*365+273=》737347, 737347/7=》105335周(星期)余2天(737347-105335*7=2)。
答:该日是周二。
二、代码法(主要用月代码推算,适合推算近期的)公式:(日期数+月代码)/4,余几(余0表示周日)就是周几。
月代码:某月最后一天是周几,就是其下月的代码。
例如,2018年12月31日是周一,那么,2019年1月的代码就是1。
例题:算2019年1月31日周几。
解:因为该1月的代码是1,所以,(31+1)/7)=>余4。
答:该日周四。
很容易就推出一年12个月的代码(2019年是144725736146),把它记住了,很快就可算出该年某日是周几。
三、三码法(主要用年月日三码推算,适用年份有限)适用2000年至2099年公式:(日码+月码+年码)/7=》余几,余几就是周几,余0就是周日。
适用1901年至1999年公式:(日码+月码+年码)/7=》余几+1,余几+1的和就是周几,其和是0就是周日。
日码:需要推算的日期数。
月码:闰年512503514624,平年622503514624。
年码:(年后两位/4+年后两位)/7=》余数(年码)。
注:(年后两位)/4取整,后两位数小于4取0。
例1、2000年3月25日周几?解:年码=》(0/4+0)/7=》余0。
故(25+2+0)/7=》余6。
答:该日周六。
例2、2020年2月29日周几?解:年码=》(20/4+20)/7=》余4。
故(29+1+4)/7=》余6。
答:该日周六。
例3、1903年4月27日周几?解:年码=》(3/4+3)/7=》余3。
故(27+5+3)/7=》余0+1=1。
答:该日周一。

计算星期几的方法计算任何一个日期是星期几的方法蔡勒公式W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 C是世纪数减1,y是年份后两位,M是月份(从3月开始,1月和2月要按上一年的13月和14月来算,这时C和y 均按上一年取值),d是日数。
求出W的值,再除以7,余几就是星期几,余数为0,则是星期天。
注意:[...]表示只取整数部分注意:公式中如计算得出负数,不能按习惯的余数的概念求余数,只能按数论中的余数的定义求余。
为了方便计算,我们可以给它加上一个7的整数倍,使它变为一个正数,比如加上7、14、21、28等,得到一个整数后,再除以7,余几,说明这一天是星期几。
例1:2004年的9月1日是星期几?C=20 y=04 M=9 d=1W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 =[20/4]-2×20+04+[04/4]+[13×(9+1)/5]+1-1=5-40+4+1+[13×2]+1-1=5-40+4+1+26+1-1=-4W为负数不行,加7的倍数14,得10。
10除以7,余数为3,2004年的9月1日是星期三。
例2:2010年的7月15日是星期几?C=20 y=10 M=7 d=15W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 =[20/4]-2×20+10+[10/4]+[13×(7+1)/5]+15-1=5-40+10+2+[13×8/5]+14=-23+20+14=1111除以7余数为4,2010年的7月15日是星期四。
链接:1世纪为100年,2000年以后为21世纪,以此类推1个年代为10年,90-99为90年代,以此类推!如:1900年是19世纪、1901年是20世纪、2000年是20世纪、2001年是21世纪。
某年某月某日星期几的计算方法首先确定公历(阳歷)12个月,每个月的代码数即:每个月号前一天是星期几,本月代码数就是几,如果是星期天,代码数就是0。
那个月几号是星期几?就把几号加上本月代码数后被7除,餘几就是星期几,除尽就是星期天。
如:2006年从1月---12月以次代码数为:6、2、2、5、0、3、5、1、4、6、2、4。
如果计算10月1日星期几?就把1号加上10月代码6等於7,能被7除尽,10月1日就是星期天。
再如:7月21日星期几?就把21加上7月代码数5等於26,被7除后餘5,7月21日就是星期五(因为21本身就能被7除尽,就不用再加代码数了,代码数是几就是星期几)。
注:如果要计算下一年每月代码数,可在上一年每月代码数上加1即可。
阳歷一年中大月为31天,小月为30天,平月(2月)为28天,闰月年为29天。
闰月年就是,年数能被4除尽的为闰月年,闰月年就要在2月加1天(2月变成29天)。
闰月年每月的代码数除1月、2月在上一年同月代码数上加1外,其他月份都在上年同月代码数上加2即可;闰月年的下一年每月的代码数除1月、2月在上一年同月代码数上加2外,其他月份在上年同月代码数上加1即可。
想知道某年某月某日星期几的计算方法?年份代码数代码0123456公历年份1923(1924)192519261927(1928)192919301931(1932)1933 19341935(1936)193719381939(1940)194119421943(1944)194519461947(1948)194919501951(1952)195319541955(1956)195719581959(1960)196119621963(1964)196519661967(1968)196919701971(1972)197319741975(1976)197719781979(1980)198119821983(1984)198519861987(1988)198919901991(1992)199319941995(1996)199719981999(2000)200120022003(2004)200520062007(2008)200920102011(2012)2013201420152016201720182019(2020)202120222023月份代码数代码(6)0(2)33614上半年月份1月2月3月4月5月6月代码625035下半年月份7月8月9月10月11月12月日期代码数代码1234560 1234567日期8910111213141516171819202122232425262728293031注:你要想查某年、某月、某日、星期几?如查:(1)、1949年10月1日星期几?1、先查1949年代码数为5;2、再查10月代码数为0;3、后查1日代码数为1。
计算星期几的方法计算星期几的方法计算任何一个日期是星期几的方法蔡勒公式W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 C是世纪数减1,y是年份后两位,M是月份(从3月开始,1月和2月要按上一年的13月和14月来算,这时C和y 均按上一年取值),d是日数。
求出W的值,再除以7,余几就是星期几,余数为0,则是星期天。
注意:[...]表示只取整数部分注意:公式中如计算得出负数,不能按习惯的余数的概念求余数,只能按数论中的余数的定义求余。
为了方便计算,我们可以给它加上一个7的整数倍,使它变为一个正数,比如加上7、14、21、28等,得到一个整数后,再除以7,余几,说明这一天是星期几。
例1:2004年的9月1日是星期几?C=20 y=04 M=9 d=1W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 =[20/4]-2×20+04+[04/4]+[13×(9+1)/5]+1-1=5-40+4+1+[13×2]+1-1=5-40+4+1+26+1-1=-4W为负数不行,加7的倍数14,得10。
10除以7,余数为3,2004年的9月1日是星期三。
例2:2010年的7月15日是星期几?C=20 y=10 M=7 d=15W = [C/4] - 2C + y + [y/4] + [13×(M+1) / 5] + d - 1 =[20/4]-2×20+10+[10/4]+[13×(7+1)/5]+15-1=5-40+10+2+[13×8/5]+14=-23+20+14=1111除以7余数为4,2010年的7月15日是星期四。
链接:1世纪为100年,2000年以后为21世纪,以此类推1个年代为10年,90-99为90年代,以此类推!如:1900年是19世纪、1901年是20世纪、2000年是20世纪、2001年是21世纪。
星期的计算公式范文
1.按照日历周历法计算星期:
日历周历法是最常用的日期计算方法,以一周七天为周期,星期一为
起始点。
按照这种方法,星期的计算公式为:
星期=(日期的天数-1)÷7+1
其中,日期的天数是指从年的1月1日开始计算,到指定日期的天数。
例如,计算2024年5月15日是星期几:
所以,2024年5月15日是星期二
2.按照ISO周历法计算星期:
ISO周历法是按照国际标准化组织(ISO)制定的一种日期计算方法,以一周七天为周期,星期一为起始点。
按照这种方法,星期的计算公式为:星期=(日期的天数-星期减数)÷7+1
其中,星期减数是指离最接近的星期一的天数。
通常,星期减数为3
或4、如果星期减数为3,那么星期减数就是指距离最近的上一个星期一
的天数;如果星期减数为4,那么星期减数就是指距离最近的上一个星期
四的天数。
例如,计算2024年5月15日是星期几:
星期减数=3
所以,2024年5月15日是星期日。
需要注意的是,不同地区可能采用不同的计算方法来确定星期,所以上述公式仅适用于按照日历周历法或ISO周历法计算星期的情况。
总结起来,计算星期的公式可以分为按照日历周历法计算和按照ISO 周历法计算两种方式,根据具体的需求和地区的习惯来选择适合的公式。
计算给定日期的星期几是一个常见的问题。
虽然在日常生活中我们可以依赖手机和计算机来帮助我们解决这个问题,但了解背后的原理是很有意义的。
下面我将详细介绍计算星期几的方法。
1.基本概念在计算星期几之前,我们首先需要了解几个基本概念:-儒略日:是从公元前4713年1月1日中午12:00开始计算的连续日期。
它是一个连续计数的时间尺度,非常方便用于天文计算。
-基准日:通常是一个已知星期几的日期,用于计算其他日期的星期几。
常见的基准日是星期一-基准日与儒略日的关系:基准日的儒略日是已知的,通过将要计算的日期的儒略日减去基准日的儒略日,可以得到它们之间的天数差。
2.计算公式下面是一个用于计算星期几的常用公式:- 周几 = (天数差 mod 7 + 基准日的星期几) mod 7这个公式的意思是,首先计算出要计算的日期和基准日之间的天数差,然后将天数差 mod 7,再加上基准日的星期几,最后再对结果进行 mod 7 操作,得到的余数就是要计算的日期的星期几。
3.具体步骤根据上述公式,计算给定日期的星期几的具体步骤如下:1)确定基准日的星期几。
例如,如果基准日是星期一,则基准日的星期几为0。
2)将要计算的日期转换为儒略日。
通过公式:儒略日=(年份+4713)*365.25-13*月份+天数,其中要注意闰年的处理。
3)计算天数差。
将要计算的日期的儒略日减去基准日的儒略日,得到它们之间的天数差。
4) 使用上述公式计算星期几。
根据天数差 mod 7 + 基准日的星期几计算得到星期几。
4.示例下面是一个具体的示例来演示计算星期几的过程:基准日期:2024年11月1日(星期一)要计算的日期:2024年11月23日基准日的星期几:11)儒略日的转换:基准日的儒略日=(2024+4713)*365.25-13*11+1=2,459,544.75要计算的日期的儒略日=(2024+4713)*365.25-13*11+23=2,459,566.752)天数差的计算:天数差=2,459,566.75-2,459,544.75=223)使用公式计算星期几:星期几 = (22 mod 7 + 1) mod 7 = 3所以,2024年11月23日是星期三5.注意事项在使用上述方法计算星期几时,需要注意以下几点:-处理闰年:闰年的2月份有29天,需要特殊处理。
星期几的速算方法
在学习了找规律以后,经常会出现一些求“某月某日”是星期几的问题。
例如:“今年一月一日是星期五,十月一日是星期几?”解这道题的一般方法是:
(1)先求出一月一日到十月一日的天数和
31+28+31+30+31+30+31+31+30+1=274(天)
(2)再求出7除天数和的余数
274÷7=39(组)……1(天)
(3)最后求出十月一日是星期几
从星期五算起,因余数是1,所以十月一日是星期五。
这种算法在求“天数和”及“余数”时,既麻烦又容易出错。
有一种求星期网几的简便速算法——“7余数”法。
“7余数”法是指一个数除以7,得到的余数。
(若一个数能被7除尽,余数为0。
)
每年各月份按天数多少分组,分别列出它们的7余数如下:
大月(31天的有:1月、3月、5月、7月、8月、10月、12月)的7余数是3。
小月(30天的有:4月、6月、9月、11月)的7余数是2。
平年二月(28天)的7余数是0。
闰年二月(29天)的7余数是1。
这样前面的题共经过五个大月三个小月和一个平月,再加网上十月一日这一天,共经过天数的7余数为:3×5+2×3+0+1=22(天),22的7余数是1。
所以今年十月一日与元旦同是星期五。
感谢您的阅读,祝您生活愉快。
计算星期几
要知道几十天以后的某一天是星期几,这是不难的,因为只要计算一下被7除的余数就可以了。
但是,如果要知道几十年以后的某一天是星期几,那就比较困难了,因为在这段时间里有闰年,而且,每个月所含的天数也不一样。
在这一节,我们要给出一个公式,可以方便地解决这个问题。
按现行的公历历法,每年有365天,若这一年是闰年,则有366天,二月有二十九天。
闰年是这样确定的:公元年份数不被100整除但被4整除,或者年份数被400整除。
如果某一年是闰年,这一年的二月比正常年份的二月多一天,这样,从这一年的三月一日开始,星期数都受到这闰月的影响,同时,这一年的一月和二月里的星期数却不受影响。
这样,就使得同一年里的计算有些不方便。
所以,为了计算方便,我们把三月一日作为计算星期数的基点。
1600年以来,全世界大部分地区使用现行的公历历法。
因此,我们考虑一个从1600年起使用的计算星期几的公式。
以下,我们使用记号:
N = 100c + y 表示年份,其中0 ≤ y ≤ 99;
m 表示月份,m = 1表示三月,m = 2表示四月, ,m = 12表示二月; d N (m )表示第N 年m 月1日的星期数。
假设d 1600(1)是已知的,我们首先计算d N (1),即第N 年3月1日的星期数。
我们知道:如果没有闰月,一年有365天,因为
365 ≡ 1 (mod 7),
所以,每过一个正常年,星期数就增加1;每过一个闰年,星期数就增加2。
以r 表示从1600年到N 年的闰年数,我们得到
d N (1) ≡ d 1600(1) + N – 1600 + r (mod 7)。
(1)
由闰年的确定方法,我们有
][][][
400
1600
100100
1600
10041600
100-+
+-+
--+=y c y c y c r
4400
10016100
400
4
25][][
][-+++---+=y c y c y c。
388400
100100
244
][][
][-++-+=y c y c y (2)
设c = 4q + s ,0 ≤ s ≤ 3,那么,由于0 ≤ y ≤ 99,100s + y < 400,所以
][
][
400
1000100
y s y +=,= 0,
因此,由式(2)得到
388400
100400244
][][
-++++=y s q c y r
388244
][
-++=q c y
388]4
[244
][
-++=c c y , (3)
r N d d N +-+≡1600)1()1(1600
3884
244
1600100)1(][][1600-+++-++≡c
c y y c d。
)7(m o d 4
4
2)1(][][
1600c y y c d +++-≡ (4) 为了确定d 1600(1)的数值,我们把一个已知的数据代人式(4),例如,我们知
道1998年3月1日是星期日,即d 1998(1) ≡ 0 (mod 7),代人式(4),得到
0 ≡ d 1600(1) - 2⋅19 + 98 +][
][
4194
98+≡ d 1600(1) + 4 (mod 7),
所以d 1600(1) = 3,即1600年的3月1日是星期三。
将这个数值代人式(4),得到
d N (1) ≡ 3 - 2c + y +][][
44
c
y +(mod 7)。
(5)
现在,我们已经能够计算N 年的3月1日是星期几。
剩下的问题是如何计算这一年的m 月k 日是星期几。
我们先计算d N (m ),即N 年m 月1日的星期数。
容易知道:
3 月是31天,所以 d N (2) ≡ d N (1) + 3 (mod 7),
4 月是30天,所以 d N (3) ≡ d N (1) +
5 (mod 7), 5 月是31天,所以 d N (4) ≡ d N (1) + 8 (mod 7),
6 月是30天,所以 d N (5) ≡ d N (1) + 10 (mod 7),
7 月是31天,所以 d N (6) ≡ d N (1) + 13 (mod 7),
8 月是31天,所以 d N (7) ≡ d N (1) + 16 (mod 7),
9 月是30天,所以 d N (8) ≡ d N (1) + 18 (mod 7), 10月是31天,所以 d N (9) ≡ d N (1) + 21 (mod 7), 11月是30天,所以d N (10) ≡ d N (1) + 23 (mod 7), 12月是31天,所以d N (11) ≡ d N (1) + 26 (mod 7), 1 月是31天,所以d N (12) ≡ d N (1) + 29 (mod 7)。
现在,计算N 年m 月k 日的星期数已经是很容易的事了。
但是,我们希望找一个更简单的公式。
从上面的数字可以看出,从3月1日到2月1日的11个月中,星期数“增加”了29天,平均每月“增加”2.6天,因此,我们来找一个形如[2.6m - a ]的公式,其中m 是月份,a 是某个适当的数。
经过验证,发现函数
f (m ) = [2.6m - 0.2] - 2满足这些条件:
f (1) = 0,f (2) = 3,f (3) = 5,f (4) = 8, ,f (12) = 29。
利用这个函数,我们得到N 年m 月1日的星期数是
d N (m ) ≡ d N (1) + {[2.6m - 0.2] - 2 }(mod 7)。
因此,N 年m 月k 日的星期数W (N , m , k )是
W (N , m , k ) = d N (m ) + k - 1 ≡ d N (1) + [2.6m - 0.2] + k – 3 (mod 7),
由式(5),得到
W (N , m , k ) ≡ k - 2c + y +][][4
4
c y
++ [2.6m - 0.2] (mod 7)。
(6)
利用上式我们就能较容易地计算出任意给定的N 年m 月k 日的星期数的星期数W (N , m , k )了。
例1 问:1976年8月6日是星期几?
解 将N = 1976,c = 19,y = 76,m = 6,k = 6代入式(6),得到
W (1976, 6, 6) ≡ 6 – 38 + 76 +][
][
4
194
76++ [2.6⋅6 – 0.2] ≡ 5 (mod 7),
即1976年8月6日是星期五。
例2 问:1978年2月24日是星期几?
解 将N = 1977,c = 19,y = 77,m = 12,k = 24代入式(6),得到
W (1977,12,24) ≡ 24 – 38 + 77 +][
][
4
194
77++ [2.6⋅12 – 0.2] ≡ 5 (mod 7),
即1978年2月24日是星期五。
注意,由例2我们看到,一月和二月分别是作为上一年的十一月和十二月。
习 题 一
1. 问:1948年2月14日是星期几?
2. 问:1999年10月1日是星期几?。