不规则图形周长的计算

三年级上册不规则图形周长计算题学习目标：掌握计算不规则图形周长的方法，提高数学计算能力。

一、引言在数学学习中，我们学习了许多规则图形的性质和计算方法，如矩形、正方形、三角形等。

今天，我们将学习如何计算不规则图形的周长，这对于我们的数学能力提高非常重要。

二、什么是不规则图形不规则图形是指边长和角度都不相等的图形。

和规则图形相比，不规则图形形状较为复杂，没有规律可循，需要我们根据具体情况进行计算。

三、计算不规则图形周长的方法要计算不规则图形的周长，我们可以采用以下方法：1. 逐边计算法这种方法适用于不规则图形的边比较少的情况。

我们可以按顺序，逐条边地计算并相加。

首先，我们需要将不规则图形画在纸上，然后使用尺子测量每条边的长度，并将每条边的长度相加，得到最终的周长。

记住要使用相同的单位进行计算。

2. 使用近似法当不规则图形边较为复杂，无法准确测量时，可以采用使用近似法来计算周长。

这种方法的主要思想是将不规则图形分割成一些可以测量的规则图形，然后计算每个规则图形的周长，最后将它们相加得到总周长。

3. 利用已学知识我们在学习其他规则图形时，已经了解到了计算周长的方法。

对于一些不规则图形，我们可以将其分解成规则图形的组合，然后使用已学知识进行计算。

例如，我们可以将一个复杂的不规则图形分解成矩形和三角形，然后计算它们的周长，并将结果相加得到总周长。

四、例题演练现在，让我们通过一些例题来巩固所学的知识。

例题1：如图所示，计算不规则图形的周长。

[图1]解答：我们可以按照逐边计算法，依次计算每条边的长度，并将它们相加。

边AB的长度为2cm，边BC的长度为3cm，边CD的长度为4cm，边DA的长度为3cm。

因此，不规则图形的周长 = 2cm + 3cm + 4cm + 3cm = 12cm。

例题2：如图所示，计算不规则图形的周长。

[图2]解答：这个不规则图形边较为复杂，不易准确测量。

我们可以使用近似法来计算。

将图形分割为矩形ABC和三角形DEF。

不规则图形的周长怎么算
不规则图形的周长就是它有几条边，就把它所有的边加起来。

一般认为不规则图形是那些不能被定义、命名的图形，通俗的说，叫不出名字的图形就是不规则图形。

不规则图形怎么求周长，可以采用以下方法：
1.分段法，计算每一段较规则的部分，然后相加。

2.围绳法，用细绳贴着周边绕一圈，就得到与周长相等的绳长。

3.线积分法，对图形的边界线做线积分，很容易得到周长。

4.图形导入autocad，然后用cad的测量功能得到周长。

5.用测距仪，绕图形走一圈，就得到周长。

常见图形的面积和周长公式
一、周长公式
1、长方形的周长＝（长宽）×2。

2、正方形的周长＝边长×4。

3、（重点）圆的周长＝圆周率×直径=2×圆周率×半径。

1。

周长计算公式大全全文共四篇示例，供读者参考第一篇示例：周长是指封闭图形边缘上所有线段的总长度。

计算周长是数学中非常基础且常见的工作，对于几何图形的周长计算，我们可以利用一些公式来简化计算过程。

下面就让我们来看一下常见图形的周长计算公式大全。

1. 矩形的周长计算公式：矩形的周长等于两倍长加两倍宽，即周长=2*(长+宽)。

3. 圆的周长计算公式：圆的周长等于直径乘以π，即周长=π*直径，或者周长=2*π*半径。

4. 椭圆的周长计算公式：椭圆的周长没有简单的解析表达式，但可以使用数值积分等方法来计算。

9. 不规则图形的周长计算公式：对于不规则图形，可以将其分解成若干简单的几何图形，计算各部分周长后相加即可得到总周长。

周长计算是几何学中的基础工作，通过寻找几何图形的规律和特点，我们可以很方便地计算出各种图形的周长。

熟练掌握各种几何图形的周长计算公式，对于解决实际问题和加深对几何学的理解都有很大帮助。

希望以上内容对您有所帮助。

第二篇示例：周长是指物体边缘的总长度，通常用于描述封闭图形（如正方形、圆等）的大小。

周长的计算可以通过不同的公式来实现，针对不同的图形有不同的计算方法。

本文将介绍一些常见图形的周长计算公式，帮助读者更好地理解周长的概念和计算方法。

一、正方形的周长计算公式正方形是一种四边相等、四角均为直角的几何图形，其周长可以通过以下公式计算：周长= 4 × 边长在正方形中，四条边的长度都相等，所以只需将一条边的长度乘以4即可得到正方形的周长。

如果一个正方形的边长为5厘米，那么它的周长为4 × 5 = 20厘米。

在圆中，半径代表从圆心到圆周上的任意一点的距离，π代表圆周长与直径的比值，约等于3.14159。

圆的周长可以通过圆的直径和半径来计算。

如果一个圆的半径为5厘米，那么它的周长为2 × 3.14159 × 5 ≈ 31.42厘米。

周长= 边1 + 边2 + 边3在三角形中，边1、边2和边3分别代表三角形的三条边的长度，因此周长的计算方法是将三条边的长度相加即可。

三年级上册不规则图形周长计算练习题本文为三年级上册不规则图形周长计算练习题。

以下是五个不规则图形，计算它们的周长。

1. 图形一：- 边长：4cm, 5cm, 6cm, 5cm- 计算周长：4 + 5 + 6 + 5 = 20cm2. 图形二：- 边长：3cm, 7cm, 4cm, 6cm- 计算周长：3 + 7 + 4 + 6 = 20cm3. 图形三：- 边长：8cm, 9cm, 7cm, 10cm- 计算周长：8 + 9 + 7 + 10 = 34cm4. 图形四：- 边长：6cm, 4cm, 5cm, 7cm- 计算周长：6 + 4 + 5 + 7 = 22cm5. 图形五：- 边长：7cm, 9cm, 5cm, 8cm- 计算周长：7 + 9 + 5 + 8 = 29cm这些不规则图形的周长分别是20cm, 20cm, 34cm, 22cm和29cm。

同学们可以通过将每边的长度相加来计算出周长。

通过这些练习题，同学们能加深对不规则图形周长的理解，并提升他们的计算能力。

请同学们注意，不规则图形的计算周长与规则图形不同。

规则图形的周长可以通过公式直接计算，而不规则图形需要逐个边长相加得出。

这些练习题可以帮助同学们熟悉不规则图形周长的计算方法。

同时，可以通过画出这些图形并将每条边的长度标出来，以便更好地理解问题。

同学们可以按照上述格式解答这些练习题，并在练习册上进行练习。

通过不断的练习，同学们将更加熟练地计算不规则图形的周长，并在数学学习中取得更好的成绩。

这份练习题可以用于课堂练习、作业练习或课后复习。

老师可以根据学生的掌握情况，适当调整练习题的难度和数量，以满足不同学生的需求。

通过不规则图形周长计算的练习，同学们将培养出对图形的观察力和计算能力，并提升他们的数学解决问题的能力。

这对于他们未来的数学学习和生活中的实际应用都具有重要意义。

希望同学们能够积极参与这些练习，提升自己的数学水平。

祝愿同学们在学习中取得好成绩！。

不规则图形的算周长方法
一天,孙老师给我们出了一道题:
让我们算出这个图形的周长.同学们绞尽脑汁也不知道答案.但有几位同学却早已想到了答案,都争先恐后的举起手来.
我想这可不是老师以前教的,它要是个正方形和长方形就好了。

该怎么算呢?
老师叫我站起来回答,我想了一会儿，突然灵光一闪，说:”把凹进去的线段向外移动,就成了一个正方形了,再用4乘一下这图形的边长,就是这个正方形的周长了.”
孙老师说:“哇，莹莹同学，你真有眼力！”
这个图形是个不规则的图形,要想算出它的周长,用平时老师教的边长乘以2这种方法绝对是不行的,
这时就要移一下,把它变成正方形,就可以算了
同学们都恍然大悟，原来这要移一移，化一化，就可以解决了，自己怎么没有想到呢！。

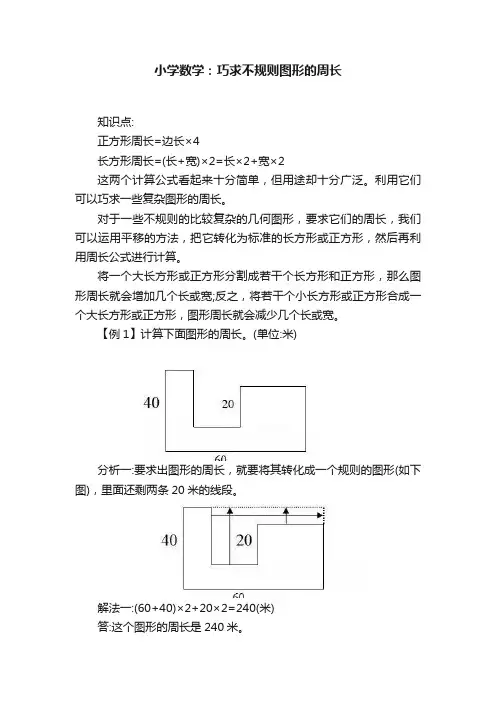
小学数学：巧求不规则图形的周长知识点:正方形周长=边长×4长方形周长=(长+宽)×2=长×2+宽×2这两个计算公式看起来十分简单，但用途却十分广泛。

利用它们可以巧求一些复杂图形的周长。

对于一些不规则的比较复杂的几何图形，要求它们的周长，我们可以运用平移的方法，把它转化为标准的长方形或正方形，然后再利用周长公式进行计算。

将一个大长方形或正方形分割成若干个长方形和正方形，那么图形周长就会增加几个长或宽;反之，将若干个小长方形或正方形合成一个大长方形或正方形，图形周长就会减少几个长或宽。

【例1】计算下面图形的周长。

(单位:米)分析一:要求出图形的周长，就要将其转化成一个规则的图形(如下图)，里面还剩两条20米的线段。

解法一:(60+40)×2+20×2=240(米)答:这个图形的周长是240米。

分析二:也可以把原图形转变成一个不封闭的图形，变成三对等长的线段(如图)。

解法二:(40+60+20)×2=240(米)答:这个图形的周长是240米。

【例2】下图是一个楼梯的侧面图，求此图形的周长。

思路导航:如果把每层台阶的宽度向上移到和最上层台阶同样高的地方，把每层台阶的高度向右移到和最下层的台阶长度一致的地方(如下图)，这样楼梯侧面图就转化为一个长方形，然后我们利用长方形周长计算公式求出此图形的周长。

(2+3)×2=10米。

【例3:进阶问题】ABCD是一个长方形，长5厘米，宽3厘米，沿对角线BD对折得到如图所示的几何图形，图中阴影部分的周长是多少厘米?解法:线段BE，DE，BC，CD的长度和就是阴影的周长。

CD=3，BC=5。

如何求BE和DE呢?长方形ABCD沿对角线BD对折后得到三角形EBD,三角形EBD就是把三角形ABD以BD为对称轴翻转之后得到的图形，(下图看的更清楚一些)即三角形ABD和三角形EBD是完全一样的。

所以BE=AB=3，DE=AD=5;所以BE+DE+BC+CD为:(5+3)×2=16(厘米)以上为极客数学整理小学数学:巧求不规则图形的周长。