2017年秋季新版北师大版九年级数学上学期4.7、相似三角形的性质导学案1

新北师大版九年级数学上册《相似三角形的性质（1）》导学案我的疑问 【合作探究】1、证明本节定理（对学、群学画出图形，写出已知、求证及证明过程并展示点评）[来源学+科+网Z+X+X+K][来源:Z 。

xx 。

][来源:]2、新知应用：课本p107例1（小组交流，全班点评展示）、【课堂小结】通过本节课学习，你有哪些收获【课后记】家长签字：【学习目标】理解并掌握相似三角形对应高的比、对应角平分线的比、和对应中线的比都等于相似比；并应用这些性质进行证明和计算。

【学习重难点】重点：利用相似三角形的性质解决计算问题。

难点：相似三角形的性质定理的证明。

【使用说明与学法指导】用8分钟左右的时间阅读课本p106-p108，认真完成导学案的问题，并把自己的疑问写出来，最后小组交流并解决。

【自主学习】 一、旧知链接：1、相似三角形的定义：三角 相等，三边 的两个三角形叫做相似三角形。

2、判定相似三角形的方法1 方法2 方法33、相似三角形的对应边 ，对应角 。

二、自主探究(仔细阅读课本p106-p107，认真填写)1、定理：相似三角形 、 、 都等于相似比。

2、如图，已知△ABC ∽△A ′B ′C ′，设△AB C 与△A ′B ′C ′的相似比为k ；点D ，E 在 BC 边上，点D ′，E ′在B ′C ′边上（1）若//////31,31C A B D A B BAC BAD ∠=∠∠=∠ 则//D A AD = 。

（2）若////31,31C B E B BC BE ==则//EA AE = （3）你还能提出哪些问题？（独学、对学）[来源学*科*网][来源:学.科.网Z.X.X.K]。

新北师大版九年级数学上册4.7.1相似三角形的性质（1）导学案学 习 目 标1、学会应用相似三角形的性质：对应高的比、对应中线的比、对应角平分线的比、周长比都等于相似比，而面积比等于相似比的平方。

2、能用来解决简单的实际问题。

重点：相似三角形的性质 难点：相似三角形性质的运用【学习过程】1、本节主要知识点：相似三角形的性质 （1） 相似三角形的对应角相等，对应边成比例；（2） 相似三角形的对应高的比、对应角平分线的比和对应中线的比都等于相似比； （3） 相似三角形周长比等于相似比；（4） 相似三角形面积比等于相似比的平方。

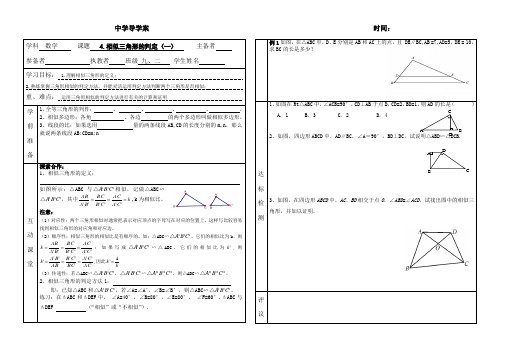
2、自主学习例1：钳工小王准备按照比例尺为3∶4的图纸制作三角形零件，如图1，图纸上的△ABC 表示该零件的横断面△A ′B ′C ′，CD 和C ′D ′分别是它们的高.（1）B A AB '',C B BC '',C A AC ''各等于多少？ （2）△ABC 与△A ′B ′C ′相似吗？如果相似，请说明理由，并指出它们的相似比.（3）请你在图1中再找出一对相似三角形.（4）DC CD''等于多少？你是怎么做的？与同伴交流解：（1）B A AB ''=C B BC ''=C A AC''=_________. （2）△ABC ∽△A ′B ′C ′ 备注（教师复备栏及学生笔记）备注（教师复备栏及学生笔记） ∵_______=_______=_______∴△ABC ∽△A ′B ′C ′( )，且相似比为___________. （3）△BCD ∽△B ′C ′D ′.（或△ADC ∽△A ′D ′C ′）∵由△ABC ∽△A ′B ′C ′得∠______=∠______ ∵∠________=∠________=_____°∴△BCD ∽△B ′C ′D ′( )（同理△ADC ∽△A ′D ′C ′） （4）∵△BDC ∽△B ′D ′C ′ ∴D C CD''= ________=________.小结1: 若△ABC ∽△A ′B ′C ′，CD 、C ′D ′是它们的__________，那么D C CD ''=CB BC''=k . 3．知识拓展： 求证1：如图2，△ABC ∽△A ′B ′C ′，CD 、C ′D ′分别是它们的对应角平分线，那么D C CD ''= C A AC ''=k . 图2求证2：如图3中，CD 、C ′D ′分别是它们的对应中线，则D C CD ''= C A AC''=k .备注（教师复备栏及学生笔装订线图3我们发现：相似三角形 的比， 的比， 的比都等于相似比例2：如图4所示，AD 是△ABC 的高，AD=h ,点R 在AC 边上，点S 在AB 边上，SR⊥AD,垂足为E .当SR=21BC 时，求DE 的长，如果SR =31BC 呢？三、达标测评：1．△ACD ∽△A ′C ′D ′，BD 和B ′D ′是它们的对应中线，已知23，，CA AC ，B ′D ′记备注（教师复备栏及学生笔记=4cm ，求BD 的长。

九年级数学（上）导学案姓名： 班级： 日期：§4.7相似三角形的性质（1）【学习内容】相似三角形的性质（P106-P108页）【学习目标】经历探索相似三角形中对应线段比值与相似比的关系的过程，理解相似三角形的性质。

利用相似三角形的性质解决一些实际问题.【自研课】定向导学 （15分钟） 对子间等级评定： ★（五星评定）对子间提出的问题： 【训练课】（时段：晚自习，时间20分钟）。

2的比例建造了模型房梁△A B C ，CD 和C D 分别是它E一填空：1、如果两个相似三角形对应边的比为3∶5 ，那么它们对应高之比是 、对应角平分线之比是 、对应中线之比是 。

2、在△ABC 中，AB=AC ，∠A=36°，∠B 的平分线交 AC 于D ， △BCD ∽△____。

3、△ABC ∽△A 1B 1C 1，，AB=4，A 1B 1=12，则它们对应边上的高的比是 ，若BC 边上的中线为1.5，则B 1C 1上的中线A 1D 1=_______ 。

4、在△ABC 中，BC=54cm ，CA=45cm ，AB=63cm ，若另一个与它相似的三角形的最短边长为15cm ，则最长边为_____5、在Rt △ABC 中，CD 是斜边AB 上的高，若BD=9，DC=4，则AD=_____，BC=_____ 二、解答题：6、△ABC ～△'''C B A ,AD 和''D A 是它们的对应角平分线，已知AD ＝8cm ，''D A ＝3cm ，求△ABC 与△'''C B A 对应高的比。

7、如图，小明自制了一个小孔成像装置，其中纸筒的长度为15cm 。

他准备了一支长为20cm 的蜡烛，想要得到高度为5cm 的像，蜡烛应放在距离纸筒多远的地方CDOBA8、如图，在△ABC 中，AB ＝5，D,E 分别是边AC 和AB 上的点，且∠ADE=∠B,DE ＝2，求BC AD •的值EDCBA9、如图，AD 是△ABC 的高，点P,Q 在BC 边上，点R 在AC 边上，点S 在AB 边上，BC ＝60CM,AD ＝40CM,四边形PQRS 是正方形 （1）△ASR 与△ABC 相似吗？为什么？（2）求正方形PQRS 的边长ED QP R SCBA今天我知道了：我发现了： 我学会了： 【教师寄语】《新课堂，我展示，我快乐，我成功》-------。

4.7.1相似三角形的性质教学设计在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1∶2的比例建造了模型房梁△A'B'C',CD和C'D'分别是它们的立柱.问题1:△ACD与△A'C'D'相似吗?为什么?如果相似,指出它们的相似比.问题2:如果CD=1.5 cm,那么模型房梁的立柱有多高?已知△ABC ∽△A ′B ′C ′， △ABC 与△A ′B ′C ′的相似比为k ，它们对应高的比是多少？对应角平分线的比是多少？对应中线的比呢？请证明你的结论.解:∵△ABC ∽△A'B'C',∴∠B=∠B'.∵AD ⊥BC ,A'D'⊥B'C',∴∠ADB=∠A'D'B'=90°. ∴△ABD ∽△A'B'D'. ∴AB ∶A'B'=AD ∶A'D'=k.师生共同总结:相似三角形对应高的比等于相似比.如图：已知△ABC ∽△A ′B ′C ′，相似比为k ，AD 平分∠BAC ，A ′D ′平分∠B ′A ′C ′; E 、E ′分别为BC 、B ′C ′的中点. 试探究AD :A ′D ′的比值关系，AE :A ′E ′呢？.,,.(1)..ABBAC B A C B B k A B AD BAC A D B A C BAD B A D BAD B A D AB BD AD k A B B AB D A D C A B C '''∴∠=∠'''∠=∠'=''∠''∠''⎡⎤'∴∠=∠'''∴'''∴===''''''⎣⎦∽，，平分平分∽两个角分别相等的两个三角形相小组解：△似△△△.,,11,22.,.,..AB BCB B k A B BC E E BC B C BE BC B E B C BE BC B E B C AB BCk A B B C AB BE k A B B E B B BAE B A E AB B ABC E AE k A B B E A E A B C '''∴∠=∠'=='''''''∴=''=''∴=''''==''''∴==''''∠=∠'∴'''∴===''''⎡⎦'⎣'⎤∽，，分别为的中点，，△∽△小组2解：△△ 小结：由此可知相似三角形还有以下性质. 相似三角形对应角平分线的比和对应中线的比都等于相似比.议一议：如图，已知△ABC ∽△A ′B ′C ′， △ABC 与△A ′B ′C ′的相似比为k ；点D 、E 在BC 边上，点D ′、E ′在B ′C ′边上.（1）若∠BAD =13∠BAC ，∠B ′A ′D ′=13∠B ′A ′C ′，则ADA ′D′等于多少?（2）若BE =13BC ， B ′E ′=13B ′C ′，则AE A ′E′等于多少？（3）你还能提出哪些问题？与同伴交流.(),,.11,,33.11()..ABBAC B A C B B k A B BAD BAC B A D B A C BAD B A D BAD B A D AB BD ADk A B B ABC A B C D A D '''∴∠=∠'''∠=∠'=''∠=∠∠'''=∠'''∴∠=∠'''∴'''∴===''''''⎡⎤⎣⎦∽，∽两个角分别相等的两个三角形相小解：△△似组△△().11,,33.,.,().2.AB BCB B k A B BC BE BC B E BE BC B E B C AB BCk A B B C AB BE k A B B E B B BAE B A E AB BE ABC A B C B C AE k A B B E A E '''∴∠=∠'==''''=''=''∴=''''==''''∴==''''⎡⎤⎣⎦∠=∠'∴'''∴===''''''∽，，∽两边成比例且夹角相等的两个三角形小组2解△△相似：△△典例精析：如图，AD 是△ABC 的高，AD =h ，点R 在AC 边上，点S 在AB 边上，SR ⊥AD ，垂足为E . 当SR =12BC 时，求DE 的长. 如果SR =13BC 呢？解：∵SR ⊥AD ，BC ⊥AD ∴SR//BC∴∠ASR=∠B ，∠ARS=∠C∴ΔASR ∽ΔABC ∴AE AD =SR BC 即AD −DE AD =SRBC. 当SR =12BC 时，得h −DE h =12.解得DE =12h.当SR =13BC 时，得h −DE h =13.解得DE =23h.归纳总结：通过类比的数学方法得到：1.两个相似三角形对应高之比为1：2，那么它们对应中线之比为（）A．1：2 B．1：3 C．1：4 D．1：8 2.在△ABC中，AB=24，AC=18，D是AC上一点，AD=12．在AB上取一点E．使A、D、E三点组成的三角形与△ABC相似，则AE的长为（）A．16 B．14 C．16或14 D．16或9 3.若两个相似三角形的相似比是2：3，则这两个三角形对应中线的比是．4.已知两个相似三角形的相似比为2：3，其中一个小三角形的最大边长为6，那么另一个三角形的最大边长为．5.如图是一个照相机成像的示意图，如果底片AB 宽40 mm，焦距是60 mm，求所拍摄的2m外景物的宽CD.。

课题：相似三角形的性质教学目标：1．经历探索相似三角形中对应线段比值与相似比的关系的过程，理解相似三角形的性质．2．培养学生的探索精神和合作意识；通过运用相似三角形的性质，增强学生的应用意识.在探索过程中发展学生类比的数学思想及全面思考的思维品质．3．利用相似三角形的性质解决一些实际问题，在探索过程中发展学生积极的情感、态度、价值观，体现解决问题策略的多样性．教学重点与难点：重点：相似三角形中对应线段比值的推导及运用相似三角形的性质解决实际问题．难点：相似三角形的性质的运用．教学过程：一、巧设情景，引入新课在前面我们学习了相似三角形的定义和判定条件，知道相似三角形的对应角相等，对应边成比例.那么，在两个相似三角形中是否只有对应角相等、对应边成比例这个性质呢？本节课我们将研究相似三角形的其他性质.活动内容：在生活中，我们经常利用相似的知识解决建筑类问题.如图，小王依据图纸上的△ABC，以1：2的比例建造了模型房梁△A′B′C′，CD和C′D′分别是它们的立柱.（1）试写出△ABC与△A′B′C′的对应边之间的关系，对应角之间的关系.（2）△ACD与△A′C′D′相似吗？为什么？如果相似，指出它们的相似比.（3）如果CD=1.5cm，那么模型房的房梁立柱有多高？（4）据此，你可以发现相似三角形怎样的性质？处理方式：以问题串的形式引导学生思考，学生讨论交流，在导学案上完成后再展示说明，学生之间互相补充，教师适时点评．设计意图：从,有利于激起学生的兴趣，感受了分类的必要性．二、提出问题，自主探索我们利用相似的判定与基本性质得到了相似三角形中一种特殊线段的关系，即对应高的比等于相似比，相似三角形中除了高是特殊线段，还有哪些特殊线段？它们也具有特殊关系吗？下面让我们一起探究活动内容1：如图：已知△ABC ∽△A ′B ′C ′，相似比为k ，AD 平分∠BAC ，A′D′平分∠B′A ′C ′；E 、E′分别为BC 、B′C′AD 与 A /D /的比值关系，AE 与A′E′呢？处理方式：通过学生小组合作探究，类比前面探究过程，在导学案上至少证明其中一个结论,完成后再展示说明，学生之间互相补充，教师适时点评．解：∵△ABC ∽△A ′B ′C ′，∴///BAC B A C ∠=∠ ，∠B =∠B ′，//AB A B=k ． ∵AD 平分∠BAC ，A ′D ′平分∠B ′A ′C ′，∴///BAD B A D ∠=∠．∴△BAD ∽△B ′A ′D ′（两个角分别相等的两个三角形相似） ∴AB BD AD k A B B D A D==='''''' ， 解：∵△ABC ∽△A ′B ′C ′，∴∠B =∠B ′，//AB BC k A B B C ==''． ∵E 、E′分别为BC 、B′C′的中点， ∴////11,22BE BC B E B C ==． ∴//BE BC B E B C =''． ∵//AB BC k A B B C ==''， ∴//AB BE k A B B E ==''． ∵∠B =∠B ′，∴△BAE ∽△B ′A ′E ′．（两边成比例且夹角相等的两个三角形相似）A B C D E A / B / C / D / E /∴//AB BE AE k A B B E A E ===''''． 设计意图：通过学生小组合作探究，类比前面探究过程，引发学生主动探究意识、培养合作交流能力，发展学生的类比的思维能力，与归纳总结能力.活动内容2：我们已经得到了相似三角形中特殊线段的关系，如果把角平分线、中线变为对应角的三等分线、四等分线、…n 等分线，对应边的三等分线、四等分线、…n 等分线，那么它们也具有特殊关系吗？下面请同学们独立探索以下问题：处理方式：学生能够根据二等分的证明过程很顺利地完成探究活动，并能够通过类比的思想总结出相关结论. 相似三角形对应角的n 等分线的比和对应边的n 等分线的比等于相似比.让学生在导学案上完成后再展示说明（1）解：∵△ABC ∽△A ′B ′C ，∴///BAC B A C ∠=∠，∠B =∠B ′， //AB A B=k ． ∵//////11,33BAD BAC B A D B A C ∠=∠∠=∠， ∴///BAD B A D ∠=∠．∴△BAD ∽△B ′A ′D ′（两个角分别相等的两个三角形相似）∴//AB A B =//BD B D =//AD A D =k ．（2）解：∵△ABC ∽△A ′B ′C ′，∴ ∠B =∠B ′，//AB A B =//BC B C =k ． ∵////11,33BE BC B E B C ==， ,;11,,3311(2),,33ABC A B C ABC A B C k D E BC D E B C AD BAD BAC B A D B A C A D AE BE BC B E B C A E''''''''''''''''∠=∠∠=∠''''''=='' 如图，已知∽与的相似比为、在边上，、在边上.(1)若则等于多少？若则等于多少？(3)你还能提出哪些问题，与同伴交流.∴//BE B E =//BC B C ． ∵//AB A B =//BC B C =k ， ∴//AB A B =//BE B E =k ． ∵∠B =∠B ′，∴△BAE ∽△B ′A ′E ′（两边成比例且夹角相等的两个三角形相似）∴//AB A B =//BE B E =//AE A E =k ． 设计意图：通过比较培养了学生观察、思考、类比、判断能力．亲身体会了数学与生活密切关系．有了前面探索的基础，学生完全有能力独立完成“变式问题”的探索，在探索过程中，发展学生类比探究的能力与独立解决问题的能力，培养学生全面思考的思维品质. 三、学以致用，尝试成功活动内容：多媒体展示如图4-32，AD 是△ABC 的高，AD=h ，点R 在AC 边上，点S 在AB 边上，SR ⊥AD ,垂足为E.当12SR BC =时，求DE 的长，如果13SR BC =呢？ 处理方式：找两名学生板演，其他同学在练习本上完成，教师巡视学生并辅导，做完后教师展示出答案先，由学生独立发现若有困难，可分组讨论交流．设计意图：运用前面所学解决问题，培养学生能发现问题和解决问题的能力.四、巩固提升，展示自我1. △ABC ∽△A ′B ′C ′， AD 和 A′D′是它们的对应角平分线．已知AD =8cm ，,,,.(().111222112333SR AD BC AD SR BC ASR B ARS C ASR ABC AE SR AD BCAD DE SR AD BC h DE SR BC DE h h h DE SR BC DE h h ⊥⊥∴∴∠=∠∠=∠∴∴=-=-==-==解：∽两角对应相等的两个三角形相似）相似三角形对应高的比等于相似比即当时，得=,解得.当时，得=,解得.A′D′=3cm求△ABC与△A′B′C对应高的比.2．如图，小强自制了一个小孔成像装置，其中纸筒的长度为15cm.他准备了一只长为20cm的蜡烛，想要得到高度为5cm的像，蜡烛应该放在距离纸筒多远的地方？3．如图，在△ABC 中，AB=5，D，E分别是边AC和AB上的点，且∠ADE=∠B，DE=2，求AD、BC的值.4．如图，在四边形ABCD中，对角线AC与BD相交于点E，且∠CAB=∠CBD，已知AB=4，AC=6，BC=5，BD=5.5，求DE的长.处理方式：学生做完后，教师出示答案，指导学生校对，并统计学生答题情况．学生根据答案进行纠错．设计意图：分层设练，使学生知识、技能螺旋式的上升，也是一种思维与能力的训练．要求学生能用相似三角形对应高的比等于相似比的性质来解决生活与生产中的实际问题.增强学生的应用意识.五、总结概括，整理知识教师指导学生总结本节课所学基本内容和存在疑惑点，建议学生积极发言，教师了解学生的掌握情况及存在问题.1.本节课有哪些收获？2.学习本节课后，还有哪些疑惑？处理方式：由学生进行课堂小结；⑴相似三角形的性质: 相似三角形对应高的比,对应角平分线的比,对应中线的比都等于相似比；⑵相似三角形对应角的n等分线的比,对应边的n等分线的比都等于相似比；设计意图：让学生梳理所学知识点，以形成完整知识结构，培养归纳概括能力和语言表达能力．评价自己的学习表现，有利于学生看到自己的优点和不足，以及今后改正的方向，同时也有助于学习习惯的培养．六、达标测试，反馈纠正A组：1．两个相似三角形的相似比为12，则对应高的比为______，则对应中线的比_____.∶3，那么对应角的角平分线的比为______.3．两个相似三角形对应中线的比为14，则对应高的比为______.B组：4．如图△ABC∽△A′B′C′，对应中线AD=6cm，A′D′=10cm，若BC=，求B′C′的长.处理方式：学生做完后，教师出示答案，指导学生校对，并统计学生答题情况．学生根据答案进行纠错．设计意图：分层设练，使学生知识、技能螺旋式的上升，也是一种思维与能力的训练．七、布置作业，落实目标课本P107 习题第1题．板书设计：§4.7 相似三角形的性质（1）定理例1：学生板演区。

4.7相似三角形的性质（一）导学案学习目标：1.探索相似三角形中对应线段的比值与相似比的关系2.能够正确地运用相似三角形的性质学习重点：相似三角形的性质一及应用。

学习难点：1.探索相似三角形性质一的过程.2.正确应用相似三角形的性质一解决问题.学习环节：学习准备—探究新知—应用新知—反思小结—达标检测—拓展延伸学习过程一、学习准备复习回顾：问题1 ：什么叫做相似三角形？问题2：我们要判别两个三角形是否相似除了用定义去判别，还有哪些方法呢？问题3：相似三角形的基本性质∵ △ABC ∽△A ′B ′C ′∴问题4 ：什么是相似比？二、探究新知探究活动一如图：△ ABC ∽△ A ′B ′C ′相似比为1：2，AD 是BC 上高， A ′D ′是B ′C ′上高。

问：''D A AD 是多少？思考：相似比为K ，AD:A'D'的值会是多少呢？证明：归纳：相似三角形的对应高之比等于探究活动二△ ABC ∽△ A'B'C'相似比为K ， △ ABC ∽△ A'B'C'相似比为K ，AD 是∠BAC 的角平分线， AE 是BC 边上的中线，A'D'是∠B'A'C'的角平分线。

A'E'是B'C' 边上的中线。

''D A AD 是多少？ ''E A AE 是多少？归纳：相似三角形的对应中线之比等于归纳：相似三角形对应角的角平分线之比归纳总结：相似三角形对应高的比、对应中线的比、对应角平分线的比都等于即时练习1．（2017•重庆）若△ABC ～△DEF ，相似比为3：2，则对应高的比为（ ）A ．3：2B ．3：5C ．9：4D ．4：92.（2016•兰州）已知△ABC ∽△DEF ，若△ABC 与△DEF 的相似比为，则△ABC 与△DEF 对应中线的比为（ ）A. B ． C ． D ．3.（2016•重庆模拟）已知△ABC ∽△DEF ，且AB=2,DE=3，则△ABC 与△DEF 对应的角平分线之比为（ ） A ．2：3 B ．3：2 C ．4：9 D ．9：4三、应用新知例1：如图4--32，AD 是△ABC 的高，AD=h,点R 在AC 边上，点S 在AB 边上，SR ⊥AD ，垂足为 E.当SR= BC 时，求DE 的长。

4.7 相似三角形性质第1课时相似三角形性质定理（一）理解相似三角形对应高比.对应角平分线比和对应中线比与相似比关系，会运用它求相关线段长.（重点）阅读教材P104107，自学“想一想” •“议一议”与“例1”，完成下列内容：（一）知识探究相似三角形对应高比•对应角平分线比.对应中线比都等于__________ .（二）自学反馈如图，已知△ ABB A A B‘ C,相似比为k, ADL BC于D, A D‘丄B‘ C 于D .（1）你能发现图中还有其他相似三角形吗？（2）△ ABC与厶A B C对应中线比.对应高比.对应角平分线比都等于________ .活动1小组讨论例如图，AD>A ABC高，AD= h,点R在AC边上，点S在AB边上,1 1SF L AD,垂足为E.当SR= 2BC时，求DE长，如果SR= 3BC呢？2 3解：T SRLAD BCL AD ••• SR/ BC.•••/ ASR=Z B,/ ARS=/ C.• △ ASR^A ABC （两角分别相等两个三角形相似）. AE SR • AD =SC 相似三角形对应高比等于相似比）,o AD- DE SR 即B€ 1 h -DE 11当SR =尹。

时,得〒=2.解得DE =尹 1h -DE 12当SR = 3BC 时,得〒=3.解得DE = 3h . 活动2跟踪训练 1. 如果两个相似三角形对应中线比为 8 : 9,贝卩它们相似比为（）A.8 : 9B.9 2 : 32.已知△ ABC^A DEF ,且相似比为 C.64 : 81D.22 : 3,则厶ABC W^ DEF 寸应高之比A.2 : 3B.3C.4 : 9D.93.如图，电灯 P 在横杆AB 正上方, AB 在灯光下影子为 CD AB// CD AB=2 m , CD= 5 m ,点P 至U CD 距离是 3 m ,则点P 到AB 距离是（ ）B.6 C. - m 5它们相似比为角平分线比为6.若厶 ABC^A A B‘ C , AD.A D 分别是△ ABC A A AD ： A D'= 3 : 4,A A B‘ C 一条中线 B‘ E '= 16 cm , 线BE=活动3课堂小结相似三角形性质定理1:相似三角形对应高比.对应角平分线比.对应中 线比都等于相似比.答案捉示【预习导学】 (一) 知识探究 相似比 (二) 自学反馈(1) △ ABD^A A B‘ □,△ AD3A A D C .(2)kD.10 空m4.如图，DE// BC 则厶 BC 交DE 于点G,则AG ： AF = .若 AD= 3, BD= 2, AF 丄,△ AGE^A5.若厶 ABB A A B‘ CB'= 13cm , 则它们对应B‘ C 高, 则厶ABC 中cm.【合作探究】 活动2跟踪训练 1.A 2.A 3.C 4.ADE ABC 3 5 AFC 3 : 5 5.3 : 26.12第2课时相似三角形性质定理（二）出示II 标理解相似三角形周长比.面积比与相似比关系，并会运用它解决相关问 题.（重点）備习出学阅读教材P10A110,自学“例2”，完成下列内容： （一） 知识探究相似三角形周长比等于 _______ ，面积比等于 ___________ . （二） 自学反馈如图，△ ABB A A B‘ C ,相似比为 k, ADL BC 于 D, A ' D 丄 B‘ C 于D .（1）你能发现图中还有其他相似三角形吗?ABC尬攻 在运用相似三角形性质时，要注意周长比与面积比之间区别, 不要混为一谈，另外面积比等于相似比平方，反过来相似比等于面积比 算术平方根.活动1小组讨论ABC (2) △ ABC W^ A B‘ C 中,例如图，将△ ABC沿BC方向平移得到△ DEF △ ABC与△ DEF重叠部分（图中阴影部分）面积是△ ABC面积一半，已知BC= 2,求厶ABC平移距离•解：根据题意，可知EG// AB.•••/ GEC=Z B,/ EGC=Z A.•••△GE OA ABC两角分别相等两个三角形相似）.S^ GEC EC E C（）2= 2（相似三角形面积比等于相似比平方），S^ ABC BC BC即2=專•E C= 2.•E C= ‘ 2.•B E= BC- EC= 2—“ 2,即厶ABC平移距离为2— 2.活动2跟踪训练AB 11. 已知△ ABB A A B‘ C，且=：,则S A ABC：S^A Z B z C =（）A B 2A.1 : 2B.2 : 1C.1 : 4D.4 : 12. 已知，△ ABC OA DEF △ ABC WA DEF面积之比为1 : 2,若BC= 1,则对应边EF长是（）A. 2B.2C.3D.423. 设两个相似多边形周长比是3 : 4,它们面积差为70,那么较小多边 形面积是( ) A.80 B.90 C.100D.1204. 若两个相似三角形周长比为2 : 3,贝卩它们面积比是 ________ .5. 如图，在正方形ABC 冲，F 是AD 中点，BF 与AC 交于点6则4 FGA 与厶BGC 面积之比是(1)求厶DEF 周长;⑵求厶DEF 面积.活动3课堂小结相似三角形性质定理2:相似三角形周长比等于相似比，面积比等于相 似比平方.答案捉示【预习导学】 (一) 知识探究 相似比相似比平方 (二) 自学反馈(1) △ ABD^A A B‘ □,△ ADC^A A D C .(2)k k 【合作探究】 活动2跟踪训练 1.C 2.A3.B4.4 : 95.1 : 46.已知△ ABB A DEFDEA B=DE 2 一 2 DE 26. (1) v AB= 3，「上DEF周长二12X3= 8(cm).(2) v矿空，.」DEF2 2 1 2面积=30X(3)2= 133(cm2).。