(完整版)18-19课时分层作业9定积分的概念

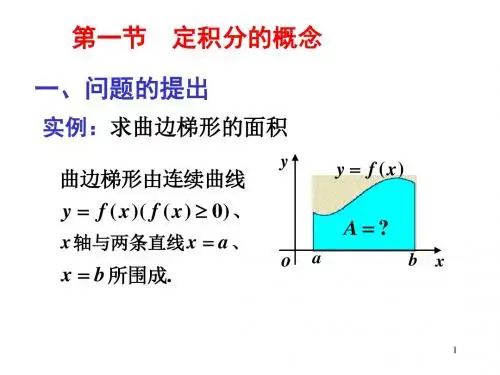
定积分的概念【知识要点】(1)定积分的定义及相关概念① 分割 如果函数f (x )在区间[a ，b ]上连续，用分点a ＝x 0<x 1<…x i －1<x i <…＜x n ＝b ，将区间[a ，b ]等分成n 个小区间，在每个小区间[x i －1，x i ]上任取一点ξi (i ＝1,2，…，n )，区间[x i －1，x i ] 的长度1i i i x x x -∆=-。

② 近似取代 “以直代取”，用矩形的面积近似代替小曲边梯形的面积，求出每个小曲边梯形面积的近似值．③ 求和 作和式i ＝1n f (ξi )Δx ＝∑i ＝1nb －anf (ξi )， ④ 取极限 当n →∞时，上述和式无限接近某个常数，这个常数叫做函数f (x )在区间[a ，b ]上的定积分，记作⎠⎛ab f (x )d x .即：()()1lim n i n i b b af x dx f a n ξ→∞=-=∑⎰ 注：在⎠⎛ab f (x )d x 中，a 与b 分别叫做积分下限与积分上限，区间[a ，b ]叫做积分区间，f (x )叫做被积函数，x 叫做积分变量，f (x )d x 叫做被积式． （2）定积分的几何意义从几何上看，如果在区间[a,b]上的函数()f x 连续且恒有()0f x ≥。

那么定积分()baf x dx ⎰表示由直线,x a x b ==（a b ≠），0y =和曲线()y f x =所围成的曲边梯形的面积。

(3 )定积分的性质 ①a b dx ba-=⎰1②⎠⎛a b kf (x )d x ＝k ⎠⎛ab f (x )d x (k 为常数)． （其中k 是不为0的常数） （定积分的线性性质）③⎠⎛a b [f 1(x )±f 2(x )]d x ＝⎠⎛a b f 1(x )d x ±⎠⎛abf 2(x )d x . （定积分的线性性质）④⎠⎛ab f (x )d x ＝⎠⎛ac f (x )d x ＋⎠⎛cb f (x )d x (其中a <c <b )． （定积分对积分区间的可加性）说明：①推广：1212[()()()]()()()bb bbm m aaaaf x f x f x dx f x dx f x dx f x ±±±=±±±⎰⎰⎰⎰②推广:121()()()()kbc c baac c f x dx f x dx f x dx f x dx =+++⎰⎰⎰⎰③性质解释：PCN M B AabOyxy=1yxOba【例题精讲】例1．计算定积分21(1)x dx +⎰分析：所求定积分即为如图阴影部分面积，面积为52。

定积分的含义和计算定积分是微积分中的一种重要概念，它表示在一定区间内的曲线与坐标轴之间的面积或者是一个变量随着另一个独立变量的变化而累积的结果。

在实际应用中，定积分可以用于求解曲线下面积、质量、体积、平均值等问题，具有广泛的应用价值。

一、定积分的定义设函数f(x)在区间[a,b]上有定义，将区间[a,b]划分成n个小区间，其中第i个小区间的长度为Δxi，区间[a,b]的分割记为P={x0,x1,…,xi,xi+1,…,xn}，则Δxi表示第i个小区间的长度。

选取小区间中任意一点ξi，构造n个函数值f(ξi)，则这些函数值的乘积f(ξi)·Δxi表示第i个小区间的面积，将这些小区间的面积加和即可得到整个区间[a,b]的面积。

当n趋于无穷大时，得到了定积分的定义：∫(a,b)f(x)dx=lim(n→∞)Σf(ξi)·Δxi其中f(ξi)表示小区间内其中一点的函数值，Δxi表示小区间的长度。

∫(a,b)f(x)dx表示在区间[a,b]上函数f(x)的定积分。

二、定积分的计算要计算一个函数的定积分，常用的方法有两种：几何方法和代数方法。

1.几何方法：利用几何图形的面积来计算函数的定积分。

将曲线与坐标轴围成的图形分为一些几何图形，计算这些图形的面积，然后将这些面积相加即可得到函数的定积分。

具体的步骤如下：（1）根据函数的特点，找到在区间[a,b]上函数的拐点，划分为多个子区间。

（2）对于每个子区间，确定曲线与坐标轴之间所构成的几何图形的公式。

（3）计算每个子区间的几何图形的面积。

（4）将各个子区间的面积相加，得到整个区间[a,b]上函数的定积分。

2.代数方法：利用微积分的基本公式和性质，将函数的定积分转化为求导或者函数原函数的问题，从而进行计算。

常用的方法有不定积分和定积分的基本性质以及换元积分法和分部积分法。

（1）基本性质：定积分具有线性性、界性、可加性、可换项性。

线性性：∫(a,b)(f(x)+g(x))dx=∫(a,b)f(x)dx+∫(a,b)g(x)dx界性：若f(x)≤g(x)，对于a≤x≤b，那么∫(a,b)f(x)dx≤∫(a,b)g(x)dx可加性：若f(x)在区间[a,b]上有定义，那么∫(a,c)f(x)dx+∫(c,b)f(x)dx=∫(a,b)f(x)dx可换项性：若f(x)在区间[a,b]上有定义，那么∫(a,b)f(x)dx=∫(a,c)f(x)dx+∫(c,b)f(x)dx（2）换元积分法：根据链式法则，将复杂的定积分转化为简单的定积分。

1.5 定积分的概念1．5.1 曲边梯形的面积1．5.2 汽车行驶的路程1．5.3 定积分的概念双基达标 (限时20分钟)1．函数f (x )＝x 2在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上， A ．f (x )的值变化很小B ．f (x )的值变化很大C ．f (x )的值不变化D ．当n 很大时，f (x )的值变化很小解析 当n 很大时，区间⎣⎢⎡⎦⎥⎤i －1n，i n 的长度1n 越来越小，f (x )的值变化很小，故选D.答案 D2．当n 很大时，函数f (x )＝x 2在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上的值可以用下列哪个值近似代替A ．f ⎝ ⎛⎭⎪⎫1nB ．f ⎝ ⎛⎭⎪⎫2nC ．f ⎝ ⎛⎭⎪⎫i n D ．f (0) 解析 当n 很大时，f (x )＝x 2在区间⎣⎢⎡⎦⎥⎤i －1n ，i n 上的值可用该区间上任何一点的函数值近似代替，也可以用左端点或右端点的函数值近似代替，故选C. 答案 C3．已知定积分∫60f (x )d x ＝8，且f (x )为偶函数，则∫6－6f (x )d x ＝A ．0B ．16C ．12D ．8解析 偶函数图象关于y 轴对称，故，故选B.答案 B 4．如图所示阴影部分的面积用定积分表示为________．答案5．若，则 lim n →∞ ∑i ＝1nf (ξi )b －a n ＝________. 解析 由定积分的定义可得．答案 66．利用定积分定义计算∫10x 3d x .解 (1)分割：0<1n <2n <…<n －1n <n n ＝1.(2)求和：⎝ ⎛⎭⎪⎫1n 3·1n ＋⎝ ⎛⎭⎪⎫2n 3·1n ＋…＋⎝ ⎛⎭⎪⎫n n 3·1n ＝∑i ＝1n ⎝ ⎛⎭⎪⎫i n 3·1n . (因为x 3连续，所以ξi 可随意取而不影响极限，故我们此处将ξi 取为[x i ，x i ＋1]的右端点也无妨)(3)取极限： lim n →∞∑i ＝1ni 3⎝ ⎛⎭⎪⎫i n 3·1n ＝ lim n →∞ 1n 4∑i ＝1n i 3＝ lim n →∞ 1n 4·⎣⎢⎡⎦⎥⎤n (n ＋1)22＝14. 此处用到了求和公式13＋23＋…＋n 3＝(1＋2＋…＋n )2＝⎣⎢⎡⎦⎥⎤n (n ＋1)22，因此∫10x 3d x ＝14. 综合提高 (限时25分钟)7．下列等式成立的是解析 由定积分的几何意义，选C.答案 C8．下列式子中不成立的是解析 分析被积函数f (x )＝sin x 和g (x )＝cos x 在各区间的图象，由定积分的几何意义，易得只有C 选项不成立，故选C.答案 C9．设f (x )是[a ，b ]上的连续函数，则的值为________． 解析 因为定积分与符号无关，所以.答案 010．利用定积分的几何意义计算⎠⎛13(x ＋2)d x 的值是________． 解析 由定积分的几何意义知⎠⎛13(x ＋2)d x 就是如图所示阴影部分的面积． 答案 811．已知汽车做变速直线运动，在时刻t 的速度为v (t )＝－t 2＋2t (单位：k m/h)，求它在1≤t ≤2这段时间行驶的路程是多少？解 将时间区间[1,2]等分成n 个小区间，则第i 个小区间为⎣⎢⎡⎦⎥⎤1＋i －1n ，1＋i n ，在第i 个时间段的路程近似为Δs i ＝v ⎝ ⎛⎭⎪⎫1＋i n Δt ＝⎣⎢⎡⎦⎥⎤－⎝ ⎛⎭⎪⎫1＋i n 2＋2⎝ ⎛⎭⎪⎫1＋i n ·1n，i ＝1,2，…，n .所以s n ＝∑i ＝1n Δs i ＝∑i ＝1n⎣⎢⎡⎦⎥⎤－⎝ ⎛⎭⎪⎫1＋i n 2＋2⎝ ⎛⎭⎪⎫1＋i n ·1n ＝－1n 3[(n ＋1)2＋(n ＋2)2＋(n ＋3)2＋…＋(2n )2]＋2n 2[(n ＋1)＋(n ＋2)＋…＋2n ] ＝－1n 3⎣⎢⎡⎦⎥⎤2n (2n ＋1)(4n ＋1)6－n (n ＋1)(2n ＋1)6＋ 2n 2·n (n ＋1＋2n )2＝－13⎝ ⎛⎭⎪⎫2＋1n ⎝ ⎛⎭⎪⎫4＋1n ＋ 16⎝ ⎛⎭⎪⎫1＋1n ⎝ ⎛⎭⎪⎫2＋1n ＋3＋1n ，s ＝S n ＝ －13⎝ ⎛⎭⎪⎫2＋1n ⎝ ⎛⎭⎪⎫4＋1n ＋161＋1n ⎝ ⎛⎭⎪⎫2＋1n ＋3＋1n ＝23， 所以这段时间行驶的路程为23 k m.12．(创新拓展)求直线x ＝0，x ＝2，y ＝0与二次函数曲线f (x )＝4x 2＋2x ＋1所围成的曲边梯形的面积．解 (1)分割：将[0,2] n 等分，则⎣⎢⎡⎦⎥⎤2(i －1)n ，2i n (i ＝1,2，…，n )的区间长度Δx ＝2n ，原曲边梯形分割成n 个小曲边梯形，如图所示．(2)用f ⎣⎢⎡⎦⎥⎤2(i －1)n 作为第i 个小曲边梯形的高作成小矩形，并用小矩形面积近似替代相应小曲边梯形面积．(3)n 个小矩形面积之和S n ＝∑i ＝1n f [2(i －1)n ]Δx ＝∑i ＝1n [16(i －1)2n 2＋4(i －1)n ＋1]2n＝⎣⎢⎡⎦⎥⎤16n 2[12＋22＋…＋(n －1)2]＋4n [1＋2＋…＋(n －1)]＋n 2n ＝32n 3·16n (n －1)(2n －1)＋8n 2·12n (n －1)＋2＝163⎝ ⎛⎭⎪⎫1－1n ⎝ ⎛⎭⎪⎫2－1n ＋4⎝ ⎛⎭⎪⎫1－1n ＋2 (4)所求曲边梯形面积S ＝ lim n →∞S n＝ ⎣⎢⎡⎦⎥⎤163⎝⎛⎭⎪⎫1－1n ⎝ ⎛⎭⎪⎫2－1n ＋4⎝ ⎛⎭⎪⎫1－1n ＋2 ＝163(1－0)(2－0)＋4(1－0)＋2＝323＋6＝503.。

课时分层作业(九) 定积分的概念(建议用时：40 分钟)[基础达标练]一、选择题1．下列结论中成立的个数是( )A．0 B．1C．2 D．3C [由定积分的概念可知②③正确，①错误，故选C.]2.关于定积分a＝ (－2)d x 的叙述正确的是( )A．被积函数为y＝2，a＝6B.被积函数为y＝－2，a＝6C.被积函数为y＝－2，a＝－6D.被积函数为y＝2，a＝－6C [由定积分的概念可知，被积函数为y＝－2，由定积分的几何意义可知a＝－6.故选C.]3.变速直线运动的物体的速度为v(t)≥0，初始t＝0 时所在位置为s0，则当t1秒末它所在的位置为( )B [由位移是速度的定积分，同时不可忽视t＝0 时物体所在的位置，故当t1秒末它所在的位置为s0＋∫t10v(t)d t.]4．若f(x)d x＝1，g(x)d x＝－3，则[2f(x)＋g(x)]d x＝( )【导学号：31062085】A．2 B．－3C．－1 D．4C [ [2f(x)＋g(x)]d x＝2 f(x)d x＋g(x)d x＝2×1－3＝－1.]5．若f(x)为偶函数，且f(x)d x＝8，则f(x)d x 等于( )A．0 B．4C．8 D．16D [∵被积函数f(x)为偶函数，∴在y 轴两侧的函数图象对称，从而对应的曲边梯形面积相等．]二、填空题6．若[f(x)＋g(x)]d x＝3，[f(x)－g(x)]d x＝1，则[2g(x)]d x＝.[解析] [2g(x)]d x＝[(f(x)＋g(x))－(f(x)－g(x))]d x＝[f(x)＋g(x)]d x－[f(x)－g(x)]d x＝3－1＝2.[答案] 27.曲线y 1y＝x，x＝2 所围成的图形面积用定积分可表示为＝与直线x.【导学号：31062086】[解析] 如图所示，阴影部分的面积可[答案]8.物体运动的速度和时间的函数关系式为v(t)＝2t(t 的单位：h，v 的单位：km/h)，近似计算在区间[2,8]内物体运动的路程时，把区间6 等分，则过剩近似值(每个ξi均取值为小区间的右端点)为km.[解析] 以小区间右端点时的速度作为小区间的平均速度，可得过剩近似值为s＝(2×3＋2×4＋2×5＋2×6＋2×7＋2×8)×1＝66(km)．[答案] 66三、解答题9.已知，求下列定积分的值．(1) (2x＋x2)d x；(2) (2x2－x＋1)d x.[解] (1) (2x＋x2)d x＝2 x d x＋x2d xe2 e32 e3＝2×＋＝e ＋.2 3 3(2) (2x2－x＋1)d x＝2x2d x－x d x＋ 1d x，因为已知，又由定积分的几何意义知： 1d x 等于直线x＝0，x＝e，y＝0，y＝1 所围成的图形的面积，所 以 1d x ＝1×e ＝e ，故(2x 2－x ＋1)d xe3 e 22 3 1 2＝2× － ＋e ＝ e － e ＋e.3 2 3 210.利用定积分的几何意义求下列定积分．(1)9－x 2d x ；(2) (2x ＋1)d x ；(3)(x 3＋3x )d x .[解] (1)曲线 y ＝ 【导学号：31062087】9－x 2表示的几何图形为以原点为圆心以 3 为半径的上半圆如图①所示．其面积为 S 1·π·32 9π.＝ ＝ 2 2由定积分的几何意义知9 9－x 2d x ＝ π.2(2) 曲线f (x )＝2x ＋1为一条直线.(2x ＋1)d x 表示直线f (x )＝2x ＋x ＝1，0，x ＝3 围成的直角梯形 OABC 的面积，如图②.1其面积为 S ＝ (1＋7)×3＝12.2 根据定积分的几何意义知(2x ＋1)d x ＝12.(3) ∵y ＝x 3＋3x 在区间[－1,1]上为奇函数，图象关于原点对称，∴曲边梯形在 x 轴上方部分面积与 x 轴下方部分面积相等．由定积分3π的几何意义知(x3＋3x)d x＝0.[能力提升练]1.已知f(x)＝x3－x＋sin x，则f(x)d x 的值为( )A．等于0 B．大于0C．小于0 D．不确定A [由题意知f(x)为奇函数，由奇函数的性质有f(x)d x＝－f(x)d x，而f(x)d x＝f(x)d x＋f(x)d x＝0.] 2.与定积分 |sin x|d x 相等的是( )C [当x∈(0，π]时，sin x≥0；当x∈(π，2 ]时，sin x＜0.∴由定积分的性质可得3.定积分x(2－x)d x 的值为. 【导学号：31062088】[解析] 因为y＝x(2－x)，2 2 2所以(x－1)2＋y2＝1，它表示以(1,0)为圆心，1 为半径的圆．定积分x(2－x)d x 就是该圆的面积的四分之一，所以定积分[答案] π4x(2－x)d x＝π.44.汽车以v＝(3t＋2)m/s 做变速直线运动时，第1 s 到第2 s 间的1 s 内经过的路程是m.[解析] 由题意知，所求路程为直线x＝1，x＝2，y＝0 与y＝3x＋21所围成的直角梯形的面积，故s＝×(5＋8)×1＝6.5(m)．2[答案] 6.55.如图1-5-5 所示，抛物线y 1＝x 将圆x ＋y ≤8 分成两部分，现在21 1向圆上均匀投点，这些点落在圆中阴影部分的概率为＋，4 6π求.【导学号：31062089】图1-5-5[解] 解方程组Error!得x＝±2.∴阴影部分的面积为.∵圆的面积为8π，4 6π∴由几何概型可得阴影部分的面积是 8π· 1 1 ＝2π 4.( ＋)＋由定积分的几何意义得，2 ＝π＋ .33。

课时分层作业(九)定积分的概念(建议用时：40分钟)[基础达标练]一、选择题1．下列结论中成立的个数是()A．0B．1C．2 D．3C[由定积分的概念可知②③正确，①错误，故选C.]2．关于定积分a＝(－2)d x的叙述正确的是()A．被积函数为y＝2，a＝6B．被积函数为y＝－2，a＝6C．被积函数为y＝－2，a＝－6D．被积函数为y＝2，a＝－6C[由定积分的概念可知，被积函数为y＝－2，由定积分的几何意义可知a＝－6.故选C.]3．变速直线运动的物体的速度为v(t)≥0，初始t＝0时所在位置为s0，则当t1秒末它所在的位置为()B[由位移是速度的定积分，同时不可忽视t＝0时物体所在的位置，故当t1秒末它所在的位置为s0＋∫t10v(t)d t.]4．若f(x)d x＝1，g(x)d x＝－3，则[2f(x)＋g(x)]d x＝()【导学号：31062085】A．2 B．－3C．－1 D．4C[[2f(x)＋g(x)]d x＝2f(x)d x＋g(x)d x＝2×1－3＝－1.]5．若f(x)为偶函数，且f(x)d x＝8，则f(x)d x等于()A．0 B．4C．8 D．16D[∵被积函数f(x)为偶函数，∴在y轴两侧的函数图象对称，从而对应的曲边梯形面积相等．]二、填空题6．若[f(x)＋g(x)]d x＝3，[f(x)－g(x)]d x＝1，则[2g(x)]d x＝________.[解析][2g(x)]d x＝[(f(x)＋g(x))－(f(x)－g(x))]d x＝[f(x)＋g(x)]d x－[f(x)－g(x)]d x＝3－1＝2.[答案] 27．曲线y＝1x与直线y＝x，x＝2所围成的图形面积用定积分可表示为________.【导学号：31062086】[解析]如图所示，阴影部分的面积可[答案]8．物体运动的速度和时间的函数关系式为v(t)＝2t(t的单位：h，v的单位：km/h)，近似计算在区间[2,8]内物体运动的路程时，把区间6等分，则过剩近似值(每个ξi均取值为小区间的右端点)为__________km.[解析]以小区间右端点时的速度作为小区间的平均速度，可得过剩近似值为s＝(2×3＋2×4＋2×5＋2×6＋2×7＋2×8)×1＝66(km)．[答案] 66 三、解答题 9．已知，求下列定积分的值．(1)(2x ＋x 2)d x ；(2)(2x 2－x ＋1)d x .[解] (1) (2x ＋x 2)d x＝2x d x ＋x 2d x＝2×e 22＋e 33＝e 2＋e 33.(2) (2x 2－x ＋1)d x ＝2x 2d x －x d x ＋1d x ，因为已知，又由定积分的几何意义知：1d x 等于直线x ＝0，x ＝e ，y ＝0，y ＝1所围成的图形的面积，所以1d x ＝1×e ＝e ， 故(2x 2－x ＋1)d x＝2×e 33－e 22＋e ＝23e 3－12e 2＋e.10．利用定积分的几何意义求下列定积分．(1) 9－x 2d x ；(2) (2x ＋1)d x ；(3)(x 3＋3x )d x .【导学号：31062087】[解] (1)曲线y ＝9－x 2表示的几何图形为以原点为圆心以3为半径的上半圆如图①所示．其面积为S ＝12·π·32＝92π.由定积分的几何意义知9－x 2d x ＝92π.(2)曲线f (x )＝2x ＋1为一条直线.(2x ＋1)d x 表示直线f (x )＝2x ＋1，x ＝0，x ＝3围成的直角梯形OABC 的面积，如图②.其面积为S ＝12(1＋7)×3＝12. 根据定积分的几何意义知(2x ＋1)d x ＝12.(3)∵y ＝x 3＋3x 在区间[－1,1]上为奇函数，图象关于原点对称， ∴曲边梯形在x 轴上方部分面积与x 轴下方部分面积相等．由定积分的几何意义知(x 3＋3x )d x ＝0.[能力提升练]1．已知f (x )＝x 3－x ＋sin x ，则f (x )d x 的值为( )A ．等于0B ．大于0C ．小于0D ．不确定A [由题意知f (x )为奇函数，由奇函数的性质有f (x )d x ＝－f (x )d x ，而f (x )d x ＝f (x )d x ＋f (x )d x ＝0.]2．与定积分|sin x |d x 相等的是( )C [当x ∈(0，π]时，sin x ≥0；当x ∈⎝ ⎛⎦⎥⎤π，3π2时，sin x ＜0.∴由定积分的性质可得 3．定积分x (2－x )d x 的值为________. 【导学号：31062088】[解析] 因为y ＝x (2－x )，所以(x －1)2＋y 2＝1，它表示以(1,0)为圆心，1为半径的圆．定积分x (2－x )d x 就是该圆的面积的四分之一，所以定积分x (2－x )d x＝π4.[答案] π44．汽车以v ＝(3t ＋2)m/s 做变速直线运动时，第1 s 到第2 s 间的1 s 内经过的路程是________m.[解析] 由题意知，所求路程为直线x ＝1，x ＝2，y ＝0与y ＝3x ＋2所围成的直角梯形的面积，故s ＝12×(5＋8)×1＝6.5(m)．[答案] 6.55．如图1-5-5所示，抛物线y ＝12x 2将圆x 2＋y 2≤8分成两部分，现在向圆上均匀投点，这些点落在圆中阴影部分的概率为14＋16π，求.【导学号：31062089】图1-5-5[解]解方程组⎩⎨⎧x 2＋y 2＝8，y ＝12x 2，得x ＝±2.∴阴影部分的面积为∵圆的面积为8π，∴由几何概型可得阴影部分的面积是8π·⎝ ⎛⎭⎪⎫14＋16π＝2π＋43.由定积分的几何意义得， ＝π＋23.。