微波实验与布拉格衍射
- 格式:docx
- 大小:247.99 KB
- 文档页数:14

微波布拉格(Bragg)衍射用微波代替X光波做布拉格衍射实验,使得了解晶格结构对波的衍射更为直观,而且对晶体的各个不同平面族赋予了几何直观性。
本实验仿照X射线通过晶体后的衍射,利用微波观察“放大了的晶体”——模拟晶体对波的衍射,并用这个装置可以测定模拟简单立方体晶体的晶格常数,并得到晶体平面族的衍射强度I随衍射角θ变化的分布曲线。
一、实验原理1.布拉格定律1912年,布拉格根据晶体内部原子平面族对入射波的反射,推导出说明X射线衍射效应的关系式。
(1)不论入射角取何种数值,在同一族中的由衍射中心阵列组成的每个单独的平面都起着平面镜的作用。
只有当反射角(即衍射角)等于入射角时,才有可能使反射波相互加强而产生最大强度。
在原子平面反射的情形下,角θ是入射束或反射束与该平面之间的夹角,不是通常光学中所指射线和平面法线之间的夹角。
(2)当一辐射束投向一族平面时,每一平面将反射一部分能量。
如图1所示,虚线相当于简单立方某一平面族,如果从O和Q发出反射波同相(相长干涉),则路程差θPQ=+QR2dsin必须等于波长的整数倍,即θ (1)2=ndλ=n,3,2,1sin路程长度NQT比MOS长了波长的整数倍,式中d是某一平面族相邻平行平面间的垂直距离。
图1 布拉格衍射示意图方程(1)就是布拉格定律,它决定晶体平行平面对波的衍射。
与对任何角度θ都能反射的平面镜不同,只有当θ取某些特殊数值时,才能满足布拉格定律,并产生相长干涉。
2、简立方晶体结构图2所示为一简单立方晶体的几族平面,可知在同一晶体中存在着不同d 值的平面族,当平面间距d 减小时,由于在平面单位面积上衍射中心数目的减小,使衍射波强度随着减小,即当d 减小时,反射变弱。
对于更复杂的晶体结构来说,这不是普遍正确的。
为了辨别不同的晶面,采用“晶面指数”(也称为密勒指数)表示。
设特定取向平面与三个坐标轴的截距分别为:z y x ,,(以三个方向上晶胞000,,c b a 为测量单位,对简单立方晶体000c b a ==),如图2(b )所示,2,4,3===z y x 的平面,求密勒指数时,取各值倒数,通分后,去掉分母,并加以括号(hkl )表示,具体做法如下:)436(126123124214131111===z y x 因此该平面的密勒指数(hkl )为(436)。

微波实验和布拉格衍射一、摘要本实验以布拉格衍射为研究对象,介绍了微波特性并简单介绍了实验原理和过程,对实验数据进行了处理,用一元线性回归和图示法进行分析并求不确定度,验证了布拉格衍射公式,加深了对实验原理的理解,并谈了实验的收获和体会。
二、实验目的1、了解微波特点,学习微波器件的使用。
2、了解布拉格衍射原理,验证布拉格公式并测量微波波长。
3、通过微波的单缝衍射和迈克尔逊干涉实验理解波动理论。
三、实验原理1、微波简介微波是一种特定波段的的电磁波,其波长在1mm~1m之间,频率为3⨯108 ~3⨯1011Hz,它波长短,频率高,穿透性强的特点,并且具有似光性-直线传播,反射和折射。
产生微波需要采用微波谐振腔和微波电子管或微波晶体管。
2、布拉格衍射原理在电磁波的照射下,晶体中每个格点上的原子或离子,其内部电子在外来电场的作用下做受迫振动,成为一个新的波源,向各方向发射电磁波,这些电磁波彼此相干,将在空间发生干涉。
干涉分为点间干涉和面间干涉N图5 布拉格衍射示意图从间距为d 的相邻两个晶面反射的两束波的波程差为2d θsin ,θ为入射波与镜面的夹角,由图知θsin 2d R Q Q P =+,当满足公式)3,2,1(s i n2 ==k k d λθ 时,形成干涉极大上面的式子称为布拉格条件布拉格公式的完整表述为:波长为λ的平面入射波入射到间距为d 的晶面族上,掠射角为θ,当满足条件)3,2,1(sin 2 ==k k d λθ时形成衍射极大,衍射线在所考虑的晶面反射方向上。
3、 单缝衍射微波的夫琅禾费衍射的强度分布可由公式I=220/sin u u I计算,其中a a u λθπ/sin =为狭缝宽度,λ为微波波长。
4、 微波的迈克尔逊干涉实验如图接收喇叭图4 微波干涉示意图在微波前进方向上反之一个与传播方向成45度的半透射半反射的分束板和A (固定反射板),B (移动反射板)两块反射板,分束板将入射波分成两列分别沿A,B 传播,两列波经分束板和并发生干涉,喇叭可给出干涉信号的强度指示。
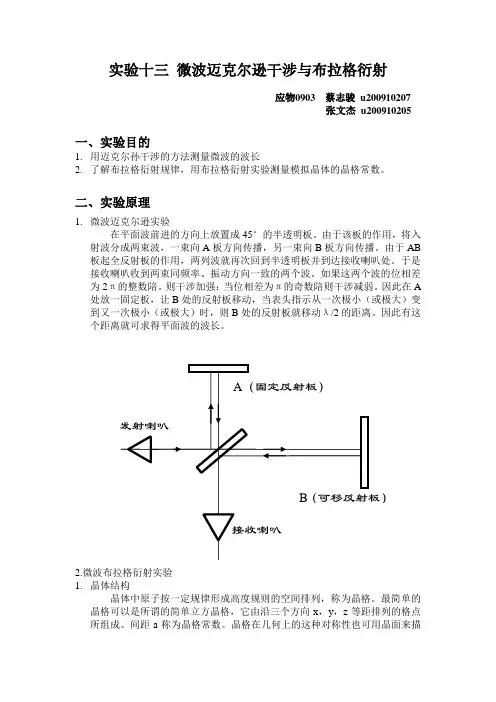
实验十三微波迈克尔逊干涉与布拉格衍射应物0903 蔡志骏u200910207张文杰u200910205一、实验目的1.用迈克尔孙干涉的方法测量微波的波长2.了解布拉格衍射规律,用布拉格衍射实验测量模拟晶体的晶格常数。
二、实验原理1.微波迈克尔逊实验在平面波前进的方向上放置成45°的半透明板。
由于该板的作用,将入射波分成两束波,一束向A板方向传播,另一束向B板方向传播。
由于AB 板起全反射板的作用,两列波就再次回到半透明板并到达接收喇叭处。
于是接收喇叭收到两束同频率、振动方向一致的两个波。
如果这两个波的位相差为2π的整数陪。
则干涉加强:当位相差为π的奇数陪则干涉减弱。
因此在A 处放一固定板,让B处的反射板移动,当表头指示从一次极小(或极大)变到又一次极小(或极大)时,则B处的反射板就移动λ/2的距离。
因此有这个距离就可求得平面波的波长。
2.微波布拉格衍射实验1.晶体结构晶体中原子按一定规律形成高度规则的空间排列,称为晶格。
最简单的晶格可以是所谓的简单立方晶格,它由沿三个方向x,y,z等距排列的格点所组成。
间距a称为晶格常数。
晶格在几何上的这种对称性也可用晶面来描述。
一个格点可以沿不同方向组成晶面,晶面取向不同,则晶面间距不同。
2.布拉格衍射晶体对电磁波的衍射是三维的衍射,处理三维衍射的办法是将其分解成两步走:第一步是处理一个晶面中多个格点之间的干涉(称为点间干涉);第二步是处理不同晶面间的干涉(称为面间干涉)。
研究衍射问题最关心的是衍射强度分布的极值位置。
在三维的晶格衍射中,这个任务是这样分解的:先找到晶面上点间干涉的0级主极大位置,再讨论各不同晶面的0级衍射线发生干涉极大的条件。
三、实验装置1. 微波迈克尔逊实验使两喇叭口方向互成90°。
半透射板与两喇叭轴线互成45,将移动版B 读书机构通过它本身上带有的两个螺钉旋入底座上,使其固定在底座上,再插上反射板A ,使固定反射板的法线与接收喇叭的轴线一致,可移动反射板B 的法线与发射喇叭轴线一致。

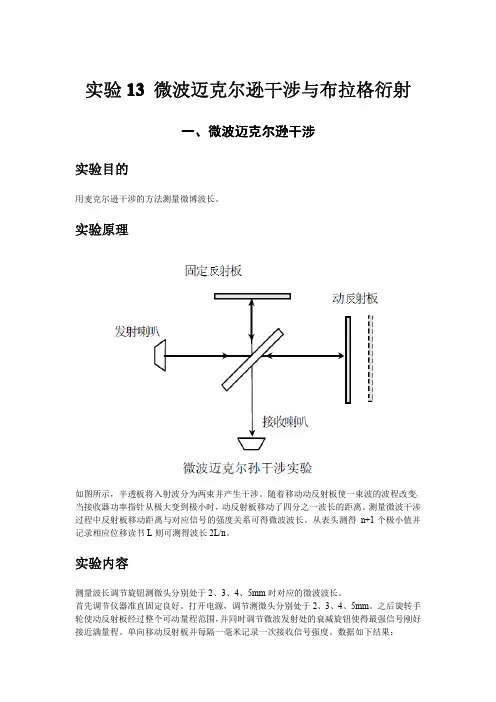
实验13 微波迈克尔孙干涉与布拉格衍射实验目的:1、用迈克尔孙干涉的方法测量微波波长;2、了解布拉格衍射规律,用布拉格衍射实验测量模拟晶体的晶格参数。
实验内容:1、测量微波迈克尔孙干涉过程中可动反射板每次移动的位移值及对应的接收信号强度。
利用不同级的干涉极大或极小的位置根据公式求微波波长。
2、对模拟晶体的100晶面、110晶面,在不同衍射角观测微波对模拟晶体的布拉格衍射信号强度,并作出衍射信号强度随角度的变化曲线图,再利用曲线图确定衍射峰的位置(角度),然后根据布拉格方程计算出模拟晶体的晶格常数。
实验原理:1、微波迈克尔孙干涉实验迈克尔孙干涉实验的基本原理如下图。
在平面波前进的方向上放置成的半透射板。
由于该板的作用,入射波将分成两束,一束向板方向传播,另一束向板方向传播。
由于这两板起全反射板的作用,两列波就再次回到半透射板并到达接收喇叭处。
于是接收喇叭收到两束同频率、振动方向一致的两个波。
如果这两个波的位相差为2π的整数倍,则干涉加强;如果位相差为π的奇数倍,则干涉减弱。
因此在板固定,板移动,当接收喇叭的表头从一次极大(或极小)变到又一次极大(或极小)时,板就移动的距离。
因此,有了这个距离,就可求得平面波的波长。
2、微波布拉格衍射实验晶格常数:晶体内的离子、原子或分子占据着点阵的结构,两相邻结点的距离就叫晶体的晶格常数。
在晶体衍射实验中,晶体是起着衍射光栅的作用。
我们可利用X射线在晶体点阵上的衍射现象来研究晶体点阵的间距和位置的排列。
常用的X射线晶体衍射方法是布拉格衍射(如下图):用波长λ的X射线射到间距为d的晶面上入射线与晶面的夹角(掠射角)为а,考虑到对称角度的散射线,则上下两相邻晶面散射X射线的光程差为。
显然使相邻晶面散射X射线发生干涉加强的条件是=nλ(n为整数)上述方程即是布拉格方程。
晶体模型图如下:实验装置:1、微波迈克尔孙干涉实验两喇叭口方向互成。
半透射板与两喇叭轴线互成,将移动板读数机构通过它本身上带有的两个螺钉旋入底座上,使其固定在底座上,再插上反射板,使固定反射板的法线与接收喇叭的轴线一致,可移动反射板的法线与发射喇叭轴线一致。

基于微波光学和布拉格衍射测量衍射角1. 引言1.1 微波光学的基本概念微波光学是光学的一个分支,研究微波波段的光学现象及其应用。
微波是一种电磁波,其波长范围通常为1mm到1m。
与可见光波长相比,微波波长更长,频率更低。
微波光学的研究对象主要是微波在各种介质中的传播和相互作用规律。
微波光学的基本概念包括折射、衍射、干涉、透射等现象。
折射是指光波从一种介质传播到另一种介质时,波的传播方向发生改变的现象。
衍射是电磁波遇到障碍物或通过狭缝时波的传播方式发生变化的现象。
干涉是两个或多个波相互叠加产生明暗条纹的现象。
透射是光波穿过物体或介质后继续传播的现象。
微波光学在科学研究和工程应用中具有重要意义,如通信、雷达、天文观测等领域都有微波光学的应用。
对微波光学的研究有助于深入了解光学原理,并为技术发展和创新提供支持。
在衍射角度测量中,微波光学的应用可以帮助准确测量物体的形状和结构,为实验结果的分析和应用提供可靠数据基础。
1.2 布拉格衍射原理简介布拉格衍射原理是由爱德华·布拉格和威廉·劳伦斯·布拉格于1913年提出的。
该原理描述了当X射线或其他波长的电磁波穿过晶体时,反射在晶体内部原子晶格结构上后,波会与自身的反射波相互干涉形成衍射图样。
这种现象导致了X射线衍射技术的发展,并在确定晶体结构中起着关键作用。
布拉格衍射原理建立在波的相位相干性和布拉格反射定律的基础上。
根据布拉格反射定律,当入射波对应的波矢K与反射波对应的波矢−K之和等于晶格的倒格矢G时,会发生构成相干的衍射峰。
这样的衍射峰对应着晶体中晶胞间距的特定数值。
布拉格衍射原理可以应用于各种波长的电磁波,包括微波光学中的微波。
通过利用布拉格衍射原理,可以实现对微波的精确测量和分析,进而用于衍射角度的测量。
在微波光学和布拉格衍射相结合的研究中,布拉格衍射原理的应用是非常重要和有效的。
2. 正文2.1 微波光学在衍射角度测量中的应用微波光学在衍射角度测量中的应用是通过微波的传播和衍射现象来测量物体的衍射角度。

实验时间:2023年3月15日实验地点:微波光学实验室实验人员:张三、李四、王五一、实验目的1. 了解微波分光仪的结构、原理及操作方法。
2. 掌握微波干涉、衍射等光学现象的基本原理。
3. 通过实验验证反射规律、单缝衍射规律以及微波的布拉格衍射规律。
4. 利用模拟晶体考察微波的布拉格衍射并测量晶格数。
二、实验原理1. 反射实验:当电磁波遇到反射板时,会发生反射现象。
反射角等于入射角,反射波与入射波同频率、同相位。
2. 单缝衍射实验:当电磁波通过一个狭缝时,会发生衍射现象。
衍射条纹间距与狭缝宽度、入射波波长有关。
3. 布拉格衍射实验:当微波入射到晶格结构中时,会发生布拉格衍射现象。
衍射角与晶格间距、入射波波长有关。
三、实验仪器1. 微波分光仪2. 反射用金属板3. 玻璃板4. 单缝衍射板5. 模拟晶体6. 频率计7. 光电探测器四、实验步骤1. 将微波分光仪连接好,打开电源,预热10分钟。
2. 将反射用金属板放置在分光仪的入射端,调整角度,观察反射现象,记录反射角度。
3. 将单缝衍射板放置在分光仪的入射端,调整狭缝宽度,观察衍射现象,记录衍射条纹间距。
4. 将模拟晶体放置在分光仪的入射端,调整入射角度,观察布拉格衍射现象,记录衍射角。
5. 使用频率计测量入射波频率,并记录数据。
6. 使用光电探测器测量衍射光强,并记录数据。
五、实验数据及结果分析1. 反射实验:入射角为θ1,反射角为θ2,θ1=θ2。
2. 单缝衍射实验:狭缝宽度为a,入射波波长为λ,衍射条纹间距为Δx,Δx=λa/d,其中d为狭缝间距。
3. 布拉格衍射实验:晶格间距为d,入射波波长为λ,衍射角为θ,θ=2arcsin(λ/2d)。
4. 通过实验验证反射规律、单缝衍射规律以及微波的布拉格衍射规律。
六、实验总结本次实验成功完成了微波分光仪的使用、反射实验、单缝衍射实验以及布拉格衍射实验。
通过实验,我们了解了微波光学的基本原理,掌握了微波干涉、衍射等光学现象的基本规律,并验证了相关理论。
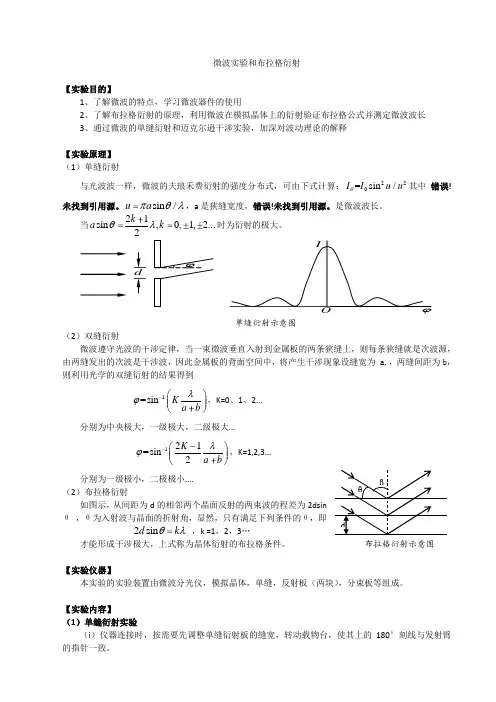
微波实验和布拉格衍射【实验目的】1、了解微波的特点,学习微波器件的使用2、了解布拉格衍射的原理,利用微波在模拟晶体上的衍射验证布拉格公式并测定微波波长3、通过微波的单缝衍射和迈克尔逊干涉实验,加深对波动理论的解释【实验原理】 (1)单缝衍射与光波波一样,微波的夫琅禾费衍射的强度分布式,可由下式计算:220=sin /I I u u θ其中 错误!未找到引用源。
sin /ua πθλ,a 是狭缝宽度,错误!未找到引用源。
是微波波长。
当21sin ,0,1, 2 (2)k a k θλ时为衍射的极大。
单缝衍射示意图(2)双缝衍射微波遵守光波的干涉定律,当一束微波垂直入射到金属板的两条狭缝上,则每条狭缝就是次波源,由两缝发出的次波是干涉波,因此金属板的背面空间中,将产生干涉现象设缝宽为 a,,两缝间距为b ,则利用光学的双缝衍射的结果得到1=sinKa bλϕ,K=0、1、2...分别为中央极大,一级极大,二级极大...121=sin2K a bλϕ,K=1,2,3...分别为一级极小,二极极小....(2)布拉格衍射如图示,从间距为d 的相邻两个晶面反射的两束波的程差为2dsin θ ,θ为入射波与晶面的折射角,显然,只有满足下列条件的θ,即2sin d k θλ ,k =1,2,3…才能形成干涉极大,上式称为晶体衍射的布拉格条件。
布拉格衍射示意图【实验仪器】本实验的实验装置由微波分光仪,模拟晶体,单缝,反射板(两块),分束板等组成。
【实验内容】(1)单缝衍射实验(i )仪器连接时,按需要先调整单缝衍射板的缝宽,转动载物台,使其上的180°刻线与发射臂的指针一致。
IOϕ(ii )把单缝衍射板放到载物台,并使狭缝所在平面与入射方向垂直,把单缝的底座固定在载物台上。
(iii )转动接收臂使其指针指向载物台的0°刻线,打开振荡器的电源,并调节衰减器,使接收电表的指示接近90μA ,记下衰减器和电表的读数。

微波光学特性和布拉格衍射实验中国海洋大学 10级海洋科学类张钰摘要用微波分光仪进行微波光学特性实验和布拉格衍射实验,验证反射定律、马吕斯定律和布拉格公式。
并在布拉格衍射实验中,提出了改进实验仪器的措施。
关键词微波光学特性,布拉格衍射实验1 引言微波有和光相似的特性,用可见光和X光所观察到的反射、干涉和衍射现象,都可以用微波再现出来。
由于微波是波长为0.01m数量级的电磁波,因此用微波设备作波动实验要显得形象、直观,更容易理解。
2 实验原理1. 微波反射实验微波是一种电磁波,遵从反射定律。
微波以入射角i入射向金属板,反射后接收到的功率最大,即反射角等于入射角。
实验时,入射角最好取30º至60º之间。
因为入射角太大接收喇叭有可能直接接受入射波。
2. 单缝衍射实验当一平面波入射到一宽度和波长可比拟的狭缝时,就要发生衍射的现象。
缝后出现的衍射波强度并不是均匀的,中央最强,同时也最宽。
在中央两侧的衍射波强度迅速减小,直至出现衍射波强度的最小值,即一级极小,此时衍射角为,其中是波长,a是狭缝宽度。
随着衍射角增大,衍射波强度又逐渐增大,直至出现一级极大值,角度为:。
原理如图1。
图1 单缝衍射原理图实验仪器布置如图2:图2 单缝衍射实验的仪器布置3. 双缝干涉实验当一平面波垂直入射到一金属板的两条狭线上,则每一条狭缝就是次级波波源。
由两缝发出的次级波是相干波。
当然,光通过每个缝也有衍射现象。
为了只研究主要是由于来自双缝的两束中央衍射波相互干涉的结果,实验中令缝宽a接近。
干涉加强的角度为,其中K=1,2,...,干涉减弱角度为:,其中K=0,1,2,...。
实验仪器布置与图2相同,只是将单缝换成双缝。
原理如图3.图3 双缝干涉实验原理图4. 迈克尔逊干涉实验图4 迈克尔逊干涉实验原理图迈克尔逊干涉实验的基本原理见上图4,在平面波前进的方向上放置成45º的半透射板。
由于该板的作用,将入射波分成两束波,一束向A方向传播,另一束向B方向传播。

物理实验报告S07微波实验和布拉格衍射作者:班级:学号:指导老师:地点:日期:六、实验数据处理(a )布拉格衍射(1)估算理论值(2)实验数据 (100)面(110)面分析实验数据可以得到以下结果 (100面):k=1(100)面:k=2(110)面:k=1(3)实验数据处理 1>验证布拉格衍射公式 根据公式sin λθ=k d100面:k=1时1θ=66.4°,k=2时2θ=36.8°; 110面: k=1时3θ=55.5°故1β误差:1∆=(68°-66.4°)/66.4°=2.4%,2β误差:2∆=(38°-36.8°)/36.8°=3.3%,3β误差:3∆=(55.5°-53°)=4.7%,误差均在允许范围内 2>计算波长及晶格常数 ①利用110面测定波长 根据公式sin λθ=k d 和晶距值求出波长值为3.40cm又()3βa u,()3βb u ∆°,故()3βu=0.289°,又()λβ=u =0.02cm ,故利用110面所测的波长为()λλ±u =(3.40±0.02)cm②利用加权平均法以及100面测定晶格常数 由公式k=1时,2cos λβ=a 得晶格常数a=4.2cm ;k=2时,co .06s 4λβ==a cm而()1β=a u=0.5°,()1β∆=b u =0.289°,故()1β=u °;同理()2β=a u=1.384°,()2β∆=b u =0.289°,故()2β=u =1.413°;故()()()1121sin 2cos ββλβ=a u u =0.106cm , ()()()2221sin 2cos ββλβ=a u u =0.079cm 故根据加权平均值()()221=∑∑i i iX X X ua u=4.503cm ,()()23214101-==⨯∑i a X u cm u故得()()4.0530.004±=±a a u cm 。

基于微波光学和布拉格衍射测量衍射角微波光学和布拉格衍射是物理学中非常重要的原理和技术,它们在材料科学、无线通信、天文学等领域都有广泛的应用。
在本文中,我们将探讨基于微波光学和布拉格衍射测量衍射角的原理和方法。
微波是一种电磁波,它的频率范围在300MHz到300GHz之间。
微波光学是将光学原理应用到微波领域的一门学科,它研究微波在各种介质中的传播、反射和衍射现象。
微波光学在通信、雷达、遥感等领域有着广泛的应用,而衍射现象则是微波光学中的重要课题之一。
布拉格衍射是指光线或波的衍射经布拉格晶格后,由布拉格晶格的衍射光程产生不同方向的干涉现象。
布拉格衍射是由法国物理学家布拉格发现的一种光的干涉现象,它在晶体学和光学中有着重要的应用。
在微波光学中,布拉格衍射也是一种常见的衍射现象,可以用来测量微波的波长和频率。
在实际的实验中,我们可以通过布拉格衍射来测量微波的波长和频率。
布拉格衍射实验通常需要使用一束微波作为入射光线,通过一个布拉格晶格后,得到衍射光谱。
根据衍射光谱的特征,我们可以计算出微波的波长和频率。
我们需要准备一个布拉格晶格,它通常由一个或多个周期性结构组成。
布拉格晶格的周期性结构可以是金属条、金属网格、薄膜或介质等。
当微波入射到布拉格晶格上时,它会经过衍射,产生不同方向的衍射光谱。
这些衍射光谱的特征可以告诉我们微波的波长和频率。
我们需要进行数据处理和分析。
通过对衍射光谱的特征进行分析,我们可以得到微波的波长和频率。
这些数据可以帮助我们更好地理解微波在布拉格晶格中的衍射现象,也可以为微波光学和通信技术的研究提供有价值的参考。
基于微波光学和布拉格衍射测量衍射角是一种常见的实验方法,它可以帮助我们测量微波的波长和频率。
通过对布拉格衍射的角度和衍射光谱的特征进行测量和分析,我们可以得到微波的波长和频率。
这些数据对于微波光学和通信技术的研究都有着重要的意义。
希望本文可以为读者对基于微波光学和布拉格衍射测量衍射角有更清晰的认识提供帮助。
基于微波光学和布拉格衍射测量衍射角全文共四篇示例,供读者参考第一篇示例:基于微波光学和布拉格衍射测量衍射角引言微波光学和布拉格衍射是现代物理学中重要的实验技术,它们被广泛应用于材料科学、光电子学和通信领域。
微波光学是研究利用微波波长进行光学实验的一门学科,它有着与可见光光学类似的原理和方法,但所使用的波长范围更大,频率更低。
布拉格衍射则是指当X射线、中子、电子或者其他波长较小的波进行衍射时,会产生布拉格衍射现象。
而衡量衍射现象的一个重要参数就是衍射角,本文将从微波光学和布拉格衍射两个方面来介绍如何测量衍射角。
微波光学测量衍射角在微波光学领域中,测量衍射角是一项重要的实验技术。
微波的波长相对较长,这就要求我们使用更大的装置来进行测量,同时要对装置进行更精密的校准和调试。
常见的微波光学实验室装置包括微波源、衍射光栅、检测器等。
我们需要确定微波的波长。
这可以通过使用微波源并将微波传输到一定距离的接收端,然后通过测量接收端接收到的微波的电磁场强度来确定波长。
一般来说,我们可以利用最小衍射原理来确定微波的波长。
在实验中,我们可以改变衍射光栅的间距或者角度,利用其中的衍射公式来计算微波的波长。
然后,我们需要构建一个合适的实验装置来测量微波的衍射角。
典型的实验装置包括微波源、平行光栅或者圆形衍射板、以及检测器。
微波源产生平行入射的微波,这些微波通过光栅或者衍射板的作用形成衍射光束,最终被检测器检测到。
我们可以通过改变衍射板的几何参数或者微波源的不同参数,来研究衍射角的变化规律。
我们需要利用适当的数据处理方法来分析实验结果。
一般来说,我们可以使用计算机来处理实验数据,例如通过拍摄衍射光斑的图像,并利用图像处理软件来测量衍射角。
我们也可以通过改变衍射板的参数,利用检测器测量出不同的衍射角,然后通过拟合方法来得到衍射角与参数之间的关系。
布拉格衍射测量衍射角布拉格衍射是材料科学和晶体学领域中重要的实验方法。
它利用晶体表面的原子排列规律对入射的波进行衍射,形成衍射现象。
微波布拉格(Bragg)衍射用微波代替X光波做布拉格衍射实验,使得了解晶格结构对波的衍射更为直观,而且对晶体的各个不同平面族赋予了几何直观性。
本实验仿照X射线通过晶体后的衍射,利用微波观察“放大了的晶体”——模拟晶体对波的衍射,并用这个装置可以测定模拟简单立方体晶体的晶格常数,并得到晶体平面族的衍射强度I随衍射角θ变化的分布曲线。
一、实验原理1.布拉格定律1912年,布拉格根据晶体内部原子平面族对入射波的反射,推导出说明X射线衍射效应的关系式。
(1)不论入射角取何种数值,在同一族中的由衍射中心阵列组成的每个单独的平面都起着平面镜的作用。
只有当反射角(即衍射角)等于入射角时,才有可能使反射波相互加强而产生最大强度。
在原子平面反射的情形下,角θ是入射束或反射束与该平面之间的夹角,不是通常光学中所指射线和平面法线之间的夹角。
(2)当一辐射束投向一族平面时,每一平面将反射一部分能量。
如图1所示,虚线相当于简单立方某一平面族,如果从O和Q发出反射波同相(相长干涉),则路程差θPQ=+QR2dsin必须等于波长的整数倍,即θ (1)2=ndλ=n,3,2,1sin路程长度NQT比MOS长了波长的整数倍,式中d是某一平面族相邻平行平面间的垂直距离。
图1 布拉格衍射示意图方程(1)就是布拉格定律,它决定晶体平行平面对波的衍射。
与对任何角度θ都能反射的平面镜不同,只有当θ取某些特殊数值时,才能满足布拉格定律,并产生相长干涉。
2、简立方晶体结构图2所示为一简单立方晶体的几族平面,可知在同一晶体中存在着不同d 值的平面族,当平面间距d 减小时,由于在平面单位面积上衍射中心数目的减小,使衍射波强度随着减小,即当d 减小时,反射变弱。
对于更复杂的晶体结构来说,这不是普遍正确的。
为了辨别不同的晶面,采用“晶面指数”(也称为密勒指数)表示。
设特定取向平面与三个坐标轴的截距分别为:z y x ,,(以三个方向上晶胞000,,c b a 为测量单位,对简单立方晶体000c b a ==),如图2(b )所示,2,4,3===z y x 的平面,求密勒指数时,取各值倒数,通分后,去掉分母,并加以括号(hkl )表示,具体做法如下:)436(126123124214131111===z y x 因此该平面的密勒指数(hkl )为(436)。
微波实验和布拉格衍射一、摘要本实验以布拉格衍射为研究对象,介绍了微波特性并简单介绍了实验原理和过程,对实验数据进行了处理,用一元线性回归和图示法进行分析并求不确定度,验证了布拉格衍射公式,加深了对实验原理的理解,并谈了实验的收获和体会。
二、实验目的1、了解微波特点,学习微波器件的使用。
2、了解布拉格衍射原理,验证布拉格公式并测量微波波长。
3、通过微波的单缝衍射和迈克尔逊干涉实验理解波动理论。
三、实验原理1、微波简介微波是一种特定波段的的电磁波,其波长在1mm~1m之间,频率为3⨯108 ~3⨯1011Hz,它波长短,频率高,穿透性强的特点,并且具有似光性-直线传播,反射和折射。
产生微波需要采用微波谐振腔和微波电子管或微波晶体管。
2、布拉格衍射原理在电磁波的照射下,晶体中每个格点上的原子或离子,其内部电子在外来电场的作用下做受迫振动,成为一个新的波源,向各方向发射电磁波,这些电磁波彼此相干,将在空间发生干涉。
干涉分为点间干涉和面间干涉N图5 布拉格衍射示意图从间距为d 的相邻两个晶面反射的两束波的波程差为2d θsin ,θ为入射波与镜面的夹角,由图知θsin 2d R Q Q P =+,当满足公式)3,2,1(s i n2 ==k k d λθ 时,形成干涉极大上面的式子称为布拉格条件布拉格公式的完整表述为:波长为λ的平面入射波入射到间距为d 的晶面族上,掠射角为θ,当满足条件)3,2,1(sin 2 ==k k d λθ时形成衍射极大,衍射线在所考虑的晶面反射方向上。
3、 单缝衍射微波的夫琅禾费衍射的强度分布可由公式I=220/sin u u I计算,其中a a u λθπ/sin =为狭缝宽度,λ为微波波长。
4、 微波的迈克尔逊干涉实验如图接收喇叭图4 微波干涉示意图在微波前进方向上反之一个与传播方向成45度的半透射半反射的分束板和A (固定反射板),B (移动反射板)两块反射板,分束板将入射波分成两列分别沿A,B 传播,两列波经分束板和并发生干涉,喇叭可给出干涉信号的强度指示。
竭诚为您提供优质文档/双击可除布拉格衍射实验报告篇一:微波布拉格衍射实验报告班级____________组别____________姓名_______学号---————日期_____________指导教师__________【实验题目】微波的布拉格衍射【实验目的】1.了解布拉格衍射原理和晶体结构知识,利用微波在模拟晶体上的衍射验证布拉格公式;2.了解并学习微波分光仪的结构和微波器件的使用。
【实验仪器】微波分光仪,模拟晶体,梳片;【实验原理】晶体对x射线的衍射实质是晶体每个格点上的原子产生的散射波的相干叠加:同一晶面上各个原子发出的散射波相干叠加,形成晶面的衍射波;同一晶面族的不同晶面的衍射波之间相干叠加。
对于同一晶面,各原子散射波相干叠加的结果遵从反射定律,即反射角等于入射角,如图2所示。
由于晶面间距为d的相邻晶面之间反射波的光程差为2dsin?,则形成干涉极大的条件为:2dsin?=k?k=1,2,3…(2)(2)式即为晶体衍射的布拉格条件。
改用入射角?表示,则(2)式可写为:2dcos?=k?k=1,2,3 (3)布拉格公式给出衍射波极大的入射角与衍射角方向,由I的极大值所对应的?,可求出晶面间距d;或已知晶面间距d,来计算I极大所对应的?。
【实验内容】1.估算理论值由已知的晶格常数a和微波波长λ,根据式2dcosβ=kλ估算出(100)面和(110)面衍射极大的入射角β2.分别测量(100)和(110)两个晶面的衍射波强度(I)和衍射角(b),绘制b~I曲线;3.衍射角(入射角)测量范围:15-80o,每隔3-5o测一个;在衍射极大附近每隔1o测一个;4..重复操作2.要求角度从小到大和从大到小测量2次;5.验证布拉格衍射公式,即将测量量与理论计算结果进行比较验证。
【原始数据及数据处理】n=(1,0,0)I1/μI2/μβ/°AA152120XX10255530403832282934505235606236616138343 840121045 895098552860346214156431306536386632326838387099100 757280801217I/μA1.51053928.551616136118.58.553.514.530.537323899.57 614.5n=(1,1,0)β/°152025303540455052545658606570758085μA111222212468678622241220XX0μA112222211508280622232210100μA111.5222211.548847962223.51.5215100I1/I2/Io/【理论值】n=(1,0,0)面d=a=4cmλ=3.3cm2dcos?=k?k=1,2(k为其它值时无意义)当k=1时cos?=0.4125β=65.7°当k=2时cos?=0.825β=34.4°n=(1,1,0)面d=a/√2=2.829cmλ=3.3cm2dcos?=k?k=1(k为其它值时无意义)当k=1时cos?=0.583β=54.4°【实验数据分析总结】由以上数据及图像可知蓝线为n=(1,0,0)面的I--?关系曲线,可知峰值有五个对应的?为20、30、35、66、70度,与理论计算所得的两个峰值位置34.465.7在误差允许范围内对应。
【关键字】实验微波干涉和布拉格衍射无线电波、光波、X光波等都是电磁波。
波长在到范围的电磁波称为微波,其频率范围从300MHz~3000GHz,是无线电波中波长最短的电磁波。
微波波长介于一般无线电波与光波之间,因此微波有似光性,它不仅具有无线电波的性质,还具有光波的性质,即具有光的直线传播、反射、折射、衍射、干涉等现象。
由于微波的波长比光波的波长在量级上大10000倍左右,因此用微波进行波动实验将比光学方法更简便和直观。
本实验就是利用波长左右的微波代替X射线对模拟晶体进行布拉格衍射,并用干涉法测量它的波长。
一、实验目的1. 了解与学习微波产生的基本原理以及传播和接收等基本特性;2. 观测微波干涉、衍射、偏振等实验现象;3. 观测模拟晶体的微波布拉格衍射现象;4. 通过迈克耳逊实验测量微波波长。
二、实验仪器DHMS-1型微波光学综合实验仪一套,包括:X波段微波信号源、微波发生器、发射喇叭、接收喇叭、微波检波器、检波信号数字显示器、可旋转载物平台和支架,以及实验用附件(反射板、分束板、单缝板、双缝板、晶体模型、读数机构等)。
三、实验原理1. 微波的产生和接收图微波产生的原理框图实验使用的微波发生器是采用电调制方法实现的,优点是应用灵活,参数调配方便,适用于多种微波实验,其工作原理框图见图。
微波发生器内部有一个电压可调控制的VCO,用于产生一个4.4GHz-5.2GHz的信号,它的输出频率可以随输入电压的不同作相应改变,经过滤波器后取二次谐波8.8GHz-9.8GHz,经过衰减器作适当的衰减后,再放大,经过隔离器后,通过探针输出至波导口,再通过E面天线发射出去。
接收部分采用检波/数显一体化设计。
由E面喇叭天线接收微波信号,传给高灵敏度的检波管后转化为电信号,通过穿心电容送出检波电压,再通过A/D转换,由液晶显示器显示微波相对强度。
2. 微波光学实验微波是一种电磁波,它和其他电磁波如光波、X射线一样,在均匀介质中沿直线传播,都具有反射、折射、衍射、干涉和偏振等现象。
北航基础物理实验研究性报告微波实验和布拉格衍射的改进自动化科学与电气工程学院第一作者:第二作者:目录摘要 (2)一、实验背景 (2)二、实验原理 (3)2.1 晶体结构 (3)2.2 布拉格衍射 (3)2.2.1 点间干涉 (3)2.2.2 面间干涉 (4)2.3 单缝衍射 (5)2.4 微波迈克尔逊干涉实验 (5)三、实验仪器 (5)四、误差分析及解决方法 (6)五、实验的改进 (6)六、实验数据的误差分析 (11)七、实验总结与反思 (12)摘要微波实验和布拉格衍射的实验,验证了布拉格公式,测定了晶格常数和微波波长。
由于实验的误差比较大,所以对实验的仪器和条件进行了一系列的改进,对误差的来源进行了更细致的分析,可以得到更加准确的结果。
一、实验背景微波是指频率为300MHz-300GHz的电磁波,是一种无线电波,即波长在1mm——1m的电磁波。
微波频率比一般的无线电波频率高,通常也称为“超高频电磁波”。
微波作为一种电磁波也具有波粒二象性。
微波与普通的电磁波一样,也存在反射,折射,衍射和偏振等现象。
因为微波的波长比普通的电磁波要短得多,又比X射线和光波长得多,所以可以用微波来仿真“晶格”衍射,“晶格”可以放大到宏观尺度,这样就方便了我们进行实验。
本实验用一束波长3cm的微波代替X射线,观察微波照射到人工制作的晶体模型时的衍射现象,模拟发生在真实晶体上的布拉格衍射,验证布拉格公式。
通过实验,人们对晶格衍射有直观的物理图像,了解三维衍射的特点和研究方法,学习有关微波器件和微波技术的知识,同时通过微波单缝衍射和迈克尔逊干涉实验,加深对场和波动概念的认识。
但由于实验仪器的限制,实验有存在着较大的误差,所以,我们可以想些方法尽可能的减小实验的误差。
二、实验原理2.1 晶体结构晶体中的原子按一定规律形成高度规则的空间排列,称为晶格。
最简单的晶格为立方晶格,它由沿三个垂直方向x 、y 、z 等距排列的格点组成。
间距a 为晶格常数,格点排列的平面称为晶面(如图 1所示)。
最常用的晶面为(100)面、(110)面、(111)面,如图。
晶面取法不同,则晶面间距不同。
相邻两个(100)面的间距等于晶格常数a ,相邻两个(110)面的间距为a √2⁄,相邻两个(111)面的间距为a √3⁄。
图 1 晶体的晶格结构和晶面2.2 布拉格衍射在电磁波的照射下,晶体中每个格点上的原子或离子,其内部的电子在外来电场的作用下做受迫振动,成为一个新的波源,向各个方向发射电磁波,这些由新波源发射的电磁波是彼此相干的,将在空间发生干涉。
这同多缝光栅的衍射很相似,晶格的格点与狭缝相当,都是衍射单元,而与光栅常数d 相当的则是晶体的晶格常数a 。
它们都反映了衍射层的空间周期,两者的区别主要在于多缝光栅是一维的,而晶体点阵是三维的,所以晶体对电磁波的衍射是三维衍射。
研究衍射问题最关心的是衍射强度分布的极值位置。
对一维光栅的衍射,极大位置由光栅方程给出:dsinθ=kλ。
在三维的晶格衍射中,这个任务是这样分解的:先找到晶面上点间干涉的0级主极大位置在讨论各不同晶面的0级衍射线发生干涉的极大条件。
2.2.1 点间干涉电磁波入射到晶面上,如图 2所示。
考虑到多个格点A1A2…B1B2…C1C2…发出的子波间的相干叠加。
这个二位点阵衍射0级主极强方向,应该符合沿此方向上所有的衍射线之间无程差。
不难想见,无程差的田间应该是:入射线与衍射线所在的平面与晶面A 1A 2…B 1B 2…C 1C 2…垂直,且衍射角等于入射角;换言之,二位点阵0级主极强方向是以晶面为镜面的反射线方向。
图 2 晶格的点间干射2.2.2 面间干涉如图 3所示,从间距为d 的相邻两个晶面反射的两束波的程差为2dsinθ,θ为入射波与晶面的掠射角。
显然,只有满足下列条件的θ,即2dsinθ=kλ (k =1,2,3,…)才能形成干涉极大。
上式称为晶体衍射的布拉格条件。
如果按照习惯使用的入射角β表示,则布拉格条件可写为 2dcosβ=kλ (k =1,2,3,…)为了观测到尽可能多的衍射极大已获得尽可能多的关于晶体结构的信息,在实际研究工作中,可以采用不同的方法。
在本实验中,入图 3 面间干涉射方向固定、波长单一的微波和“单晶”模型,采用转动晶体模型和接收喇叭的方法来研究布拉格衍射。
2.3单缝衍射和声波、光波一样,微波的夫琅禾费单缝衍射的强度分布可由下式计算,即⁄Iθ=(I0sin2u)u2⁄,a是狭缝的宽度,λ是微波的波长。
如果求式中u=(πasinθ)λ出例如±1级的强度为零处所对应的角度θ,则λ可按下式算出,即λ=a∙sinθ2.4微波迈克尔逊干涉实验如图4所示,在微博前进方向上放置一个与传播方向成45°角的半透射、半反射的分束板和A、B两块反射板。
分束板将入射波分成两列,分别沿A、B方向传播。
由于A、B板的反射,两列波又经分束板汇合并发生干涉。
接收喇叭可给出干涉信号的强度指示。
如果A板固定,当B移动过程中喇叭接收信号从一次极小变到另一次极小时,B移动的距⁄,因此测量B移动的距离也可求出微博的波长。
离为λ2图 4 微波迈克尔逊干涉仪三、实验仪器微波分光仪(如图5所示)、三厘米固态振荡器、模拟晶体、单缝板、反射板、分束板等。
四、误差分析及解决方法1、小球不等距,使a的值误差偏大——改善模型构造;2、人眼误差,观察极小值出现时,判断不准确,导致读数误差偏大;3、微波分光仪不稳定,无法保持转角在某一固定值——增加雨伞结构;4、微波迈克尔逊干涉实验中,两反射镜面不相互垂直——增加垂直导槽。
五、实验的改进布拉格衍射实验1、实验改进(1)微波分光仪机构改进针对布拉格衍射的公式验证实验,在实验中,需要转动载物台和接收臂,使实验的效率较低,操作性差,需要两人协助完成(一个人转动载物台,另一个人转动接收臂,观察电表,进行读数)如图-6。
.所以设想将微波分光仪装置进行改进,只转动接收臂,带动发射臂转动,接收臂转动多少度就带动发射臂转动多少度,使入射角和出射角始终保持相同,模型不动。
为提高实验的效率以及精确度可对微波分光仪进行如下改进(如图-7):接收臂发射臂载物台图-6 改进前的微波分光仪装置简图附加装置接收臂发射臂载物台图-7改进后的微波分光仪装置简图通过一个附加的类似于雨伞结构的的装置,可以保证接收臂在转动的同时带动发射臂转动相同的角度,而无需转动载物台,从而达到入射角和出射角相同的目的。
这样就可以一边转动发射臂,一边进行读数,找到使电流表读数最大的位置,提高了实验的效率和精确度。
(2)微波分光仪读数装置的改进由于分光仪指针读数时存在着比较大的误差,很难准确定位示数最大的点。
所以,用电子读数系统代替指针读数,可以大大提高实验的准确性。
(3)在验证布拉格衍射公式的实验中用图-9的结构来代替图-8的晶体的晶格结构,图-8图-9存在的问题:○1由于实体结构本身的精度限制,对实验的准确性会造成一定能够的误差。
每个“原子”位置并不是很精确,高低,左右都存在着误差,而且随环境条件的变化会有些变形等等,会造成比较大的误差。
○2固定在支座上也会出现一些角度的偏差,没有使所需要的(1 0 0或(1 1 0)面的法线与0刻度线重合(如图-8)图-10改进的方案:○1将模型的底座安装在穿过圆珠的尼龙线穿过的面,就可以克服中部的圆珠由于重力下坠产生的误差(如图-11)。
改装前图-11 改装后○2可以用密度较小的圆珠代替现有的圆珠以减小误差。
○3用抗变形能力强的材料来代替木质框架结构,这样可以尽可能的使晶格结构更加精密。
微波的迈克尔逊干涉实验1、实验改进1、由于A,B两板固定在仪器上时是用肉眼观测其是否垂直,这样就会产生比较大的误差,所以可以对A,B两板的固定方式进行改进,使两板的固定位置更准确。
改进方式如下:将A,B两板固定于如图示的导槽A,B两个位置,由于导槽是相互严格垂直的,这样就保证了A,B的相互垂直,再将导槽固定在载物台上,调整导槽到合适位置,这样A板就固定在导槽上,B板可以沿着其法线方向前后移动,就达到了实验的要求,而且降低了实验的误差。
(如图-13)AB图-132、读数装置改进实验中,要求准确找到极大值或极小值的位置,现有的实验仪器基础上会产生很大的误差,如果对实验的读数装置进行改进,提高精度,就可提高实验的准确率。
改进方法同布拉格衍射的读数装置改进。
3、外部环境的改进在实验室中进行实验,由于各组发出的信号之间有干扰,所以的各组实验应该隔离开来来做,以免发出的信号互相影响,这样可以提高实验的准确性。
六、实验数据的误差分析布拉格衍射实验数据如下:误差:β1平均-β1理论=2.565°相对误差:3.9%β2平均-β2理论=1.08° 3.0%β3平均-β3理论=0.42° 1.1%根据实验结果以及相对误差给分析可知,在误差允许范围内,能够验证布拉格衍射公式。
但是,实验中由于实验仪器精度和读数误差,实验结果仍存在较大误差,下面针对由晶格常数求波长的数据处理进行定量的误差分析:已知:a=4.00cm;(1 0 0)面k=1;β=68.975°。
∴d=a/√2=2.83cm∴λ=2dcosβ=3.202cm误差定量分析:实验操作中,由于人眼读书时存在误差,理论上人言分辨率的误差为0.2div,但实际上,由于需要读载物台分读盘和电流表的读数,实验中积累的人眼读数的误差将近0.5°,此误差构成A类不确定度,而在之前的实验数据处理中,忽略了这一误差认为A类不确定度为0。
电表读数的误差为 =a%·Nm=0.5°,构成B类不确定度。
∴u a=0.5°;u b=0.5°/√3=0.289°∴u(β)=√u a2+u b2=0.5773°=0.0101rad∵λ=2dcosβ;∴dλ=-2dsinβdβ;∴u(λ)=2dsinβu(β) ;∴u(λ)= 0.0478cm∴λ±u(λ)=(32.0+0.5)mm.经过对误差的定量分析,实验的结果更精确了一些。
七、实验总结与反思本实验不仅让我们对微波的特点有了一定的了解,验证了布拉格衍射原理,加深了对波动理论的理解。
同时也增强了我们的动手能力,拓展了我们的思维。
通过写研究性报告,我们对实验进行了进一步的分析,对实验的原理充分的理解后,提出了自己的一些实验改进意见,对误差的来源进行了定量的分析,整个过程下来使我们掌握了一些物理实验的研究方法,大大启发了我们的物理思维,使我们的思维更加严谨,对待科学的态度更加认真,对我们今后的学习和科研起到了十分积极的作用。
学习物理实验这门课程,不仅仅是完成学科任务,掌握科学知识,更重要的是对我们个人能力的一种锻炼。