模态分析理论基础
- 格式:pdf
- 大小:119.41 KB
- 文档页数:6

模态分析中的几个基本概念物体按照某一阶固有频率振动时,物体上各个点偏离平衡位置的位移是满足一定的比例关系的,可以用一个向量表示,这个就称之为模态。
模态这个概念一般是在振动领域所用,你可以初步的理解为振动状态,我们都知道每个物体都具有自己的固有频率,在外力的激励作用下,物体会表现出不同的振动特性。
一阶模态是外力的激励频率与物体固有频率相等的时候出现的,此时物体的振动形态叫做一阶振型或主振型;二阶模态是外力的激励频率是物体固有频率的两倍时候出现,此时的振动外形叫做二阶振型,以依次类推。
一般来讲,外界激励的频率非常复杂,物体在这种复杂的外界激励下的振动反应是各阶振型的复合。
模态是结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。
这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。
有限元中模态分析的本质是求矩阵的特征值问题,所以“阶数”就是指特征值的个数。
将特征值从小到大排列就是阶次。
实际的分析对象是无限维的,所以其模态具有无穷阶。
但是对于运动起主导作用的只是前面的几阶模态,所以计算时根据需要计算前几阶的。
一个物体有很多个固有振动频率(理论上无穷多个),按照从小到大顺序,第一个就叫第一阶固有频率,依次类推。
所以模态的阶数就是对应的固有频率的阶数。
振型是指体系的一种固有的特性。
它与固有频率相对应,即为对应固有频率体系自身振动的形态。
每一阶固有频率都对应一种振型。
振型与体系实际的振动形态不一定相同。
振型对应于频率而言,一个固有频率对应于一个振型。
按照频率从低到高的排列,来说第一振型,第二振型等等。
此处的振型就是指在该固有频率下结构的振动形态,频率越高则振动周期越小。
在实验中,我们就是通过用一定的频率对结构进行激振,观测相应点的位移状况,当观测点的位移达到最大时,此时频率即为固有频率。
实际结构的振动形态并不是一个规则的形状,而是各阶振型相叠加的结果。
固有频率也称为自然频率( natural frequency)。

模态分析的基础理论模态分析是一种研究系统中不同模式的分布、生成和演化规律的方法。
在这个理论中,模态是指系统中不同状态或形式的存在形式,例如质量分数、温度、湿度等。
模态分析的基础理论包括概率论、统计学和模态分析技术等。
概率论是模态分析的基础之一、它研究随机事件的发生概率和规律。
在模态分析中,我们可以利用概率论来描述不同模态出现的概率分布,并通过分析系统中的模式,得出不同模态的生成规律。
通过概率论的方法,我们可以预测不同模态的变化趋势,从而指导系统的优化设计和运行管理。
统计学也是模态分析的基础理论之一、统计学研究如何收集、处理、分析和解释数据,通过对大量数据的统计分析,揭示数据背后的规律和趋势。
模态分析中,统计学的方法可以用于分析模态数据的分布情况,寻找模态之间的相关性和影响因素,并建立相应的模型来预测和优化系统的运行情况。
在模态分析技术方面,主要包括聚类分析、主成分分析和模态分析方法等。
聚类分析是一种将相似的对象分组的方法,通过对模态数据进行聚类分析,我们可以将相似的模态归为一类,从而描述系统中的不同模态分布情况。
主成分分析是一种降维技术,它可以将高维的模态数据降低到低维,并保留大部分信息。
这可以帮助我们更好地理解系统模态之间的关系和重要性。
模态分析方法包括有限元模态分析、频响函数法和模态参数识别等。
通过这些方法,我们可以对系统的模态进行分析,包括振型、频率和阻尼等,并找出模态的摄动源和分布规律。
模态分析的基础理论对于理解和优化系统具有重要意义。
通过对模态的分析和研究,我们可以了解系统的特性和不同模态之间的关系,从而指导系统的设计和运行。
同时,模态分析也可以帮助我们发现和解决系统中存在的问题,提高系统的稳定性和可靠性。
因此,深入理解和应用模态分析的基础理论对于各个领域的研究和实践具有重要价值。

实验模态分析第三章:实验模态分析的基本理论振动系统的特性可以用模态来描述:固有频率、固有振型(主振型)、模态质量、模态刚度和模态阻尼等。
建立用模态参数表示的振动系统的运动方程并确定其模态参数的过程使称为模态分析。
—种理解可以认为,振动系统的物理模型、物理参数和以物理参数表示的运动方程都是已知的,引入模态参数、建立模态方程的目的是为了简化计算,解除方程耦合,缩减自由度。
另一种理解可以认为,通过对实际结构的振动测试,识别振动系统的模态参数,从而建立起系统的以模态参数表示的运动方程,供各种工程计算应用。
试验模态分析指的是后一种过程,即通过振动测试(称模态试验),识别模态参数,建立以模态参数表示的运动方程这样一个过程。
1 多自由度系统振动基础回顾&&&++=M x C x K x f t []{}[]{}[]{}{()} 2实模态理论一个n 自由度线性定常振动系统,其运动方程可以如下表示:现对两端作付氏变换得:[]{}[]{}[]{}{()}M x C xK x f t ++=&&&2([][][]){()}{()}M j C K X F ωωωω−++=式中和分别是x(t)和F(t)的付氏变换,并有()X ω()F ω()()j t X x t e dt ωω+∞−−∞=∫()()j t F f t e dtωω+∞−−∞=∫(){()}{()}Z X F ωωω=111212122212()()()()()()()()()()n n n n nn Z Z Z Z Z Z Z Z Z Z ωωωωωωωωωω⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦L L L L L L L 1()[()]{()}{()}{()}X Z F H F ωωωωω−==2[][][]K M j C ωω=−+阻抗矩阵中各元素值无法在实际振动测试中获得,因为人们不可能在实际结构上固定其它坐标,令其不动,仪留下J坐标,待其作出响应;也不可能仅使某个坐标运动,在其余坐标上测量力。




点,有图可知节点并不唯一,而且修改前后节点的位置未变。
对应尽可能避开结构振动的节点,以免给测量带来误差。
4.4试验模态分析试验模态分析的目的是为了验证理论模态分析的正确性的基础上进行深入研究奠定基础。
4.4.1试验模态分析的理论基础阻1所以在进行模态实验为在理论模态分析在物理坐标下,描述N自由度离散振动系统的运动微分方程为阻】耕+【c】扛}+医】M=沙}(4.2)式中:【M]——质量矩阵(对称且正定),M∈R~,【C】——阻尼矩阵,C∈R“”,晖】——刚度矩阵(对称且正定或半正定),K∈R“”,{x),{卦,{封——N维位移、速度和加速度响应向量,{厂(r))——_N维激振力向量。
设系统的初始状态为零,对式(4.2)两边进行拉普拉斯变换可得([Mls2“C]s+【K]){X0))=【Z(s)]{工0))={F0))式中的矩阵【Z(s)]-([M]s2+[c]s+[K】)反映了系统的动态特性,称为系统动态矩阵或广义阻抗矩阵,其逆阵[日(5)】=[Z(s)】~=(【M]s2+【C]s+[K])。
1称为广义导纳矩阵,也就是传递函数矩阵。
由式(2.2)可知{x(J))_【日0)】(F(J)}在上式中.令S=joJ,即可得到系统在频域内输出和输入的关系式{并(国)}=【日(脚)】(F(国))(4.3)(4.4)(4.5)(4.6)(4.7)式中[H(co)】为频率响应函数矩阵。
[H(∞)】矩阵中第f行_,列的元素%(叻2篇(48)表示仅在』坐标激振(其余坐标激振力为零)时,i坐标的响应与激振力之比。
在式(4.4)中令S=_,∞,可得阻抗矩阵[z(∞)】=([K]一曲2【吖])+jco[C](4.9)它和导纳矩阵有类似式(4.5)的关系[日(珊)]=[z(国)】~={(【置卜。
2[^卅)+jco[C】}1(4.10)对于一般机械、结构,假设矩阵[c]也对称,这样矩阵【z(∞)】对称,频率响应函数矩阵[日@)]也对称,故有q(脚)=HⅣ(03)(4.11)上式反映了机械、结构频率响应有互易性,可作为频率响应测试精度的一项重要检验手段。



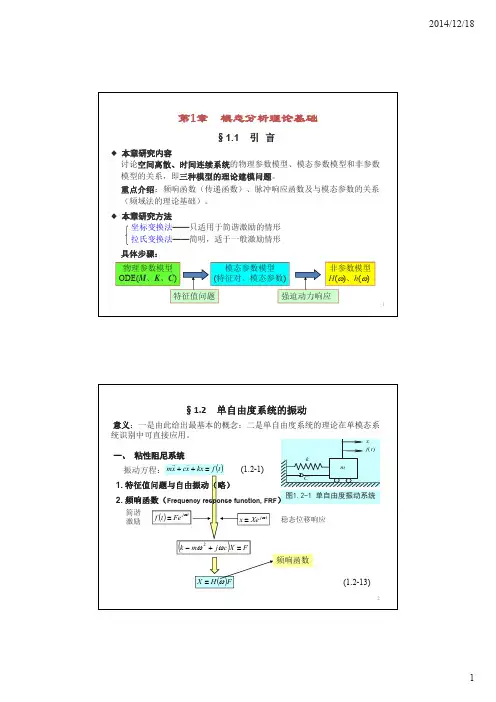
精心整理模态分析指的是以振动理论为基础、以模态参数为目标的分析方法。
首先建立结构的物理参数模型,即以质量、阻尼、刚度为参数的关于位移的振动微分方程;其次是研究其特征值问题,求得特征对(特征值和特征矢量),进而得到模态参数模型,即系统的模态频率、模态22¨330m 0z k 2k k z 000m 0k k z 0z +--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦(9) 定义主振型由于是无阻尼系统,因此系统守恒,系统存在振动主振型。
主振型意味着各物理坐标振动的相位角不是同相(相差0o )就是反相位(相差180o ),即同时达到平衡位置和最大位置。
主振型定义如下:()i i j ωt+i i sin ωt+=Im(e )φφi mi mi z =z z (10)其中为第i 阶频率下,各自有度的位移矢量,为第i 个特征矢量,表示第i 阶固有频率下的振型,i ω为第i 阶频率下的第i 个特征值,i φ为(去除项化简得以矩阵的形式展开得:2i 2i mi 2i k-ωm -k 0-k 2k-ωm -k z =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(15)有非零解,则2i 2i 2i k-ωm -k 0-k 2k-ωm -k =00-k k-ωm ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦(16)即()234222ω-m ω+4km ω-3k m =0(17)阶固有频率,每一个特征根对应一个特征矢量,表示对应模态下该由式3i i 21=z k 如果设定了1z 值,则就可以求出三个特征根值下,2z 和3z 相对于1z 的位移。
假设m=k=1, 一阶模态,1ω=0:21z =1z ,31z =1z ,即;二阶模态,223kω=m :21z=0z,31z=-1z,即;三阶模态,23kω=m :21z=-2z,31z=1z,即。
运动方程的解耦图错误!未指定顺序。
运动方程解耦过程在进行坐标变换之前需对刚度矩阵和质量矩阵进行归一化。
模态分析指的是以振动理论为基础、以模态参数为目标的分析方法。
首先建立结构的物理参数模型,即以质量、阻尼、刚度为参数的关于位移的振动微分方程;其次是研究其特征值问题,求得特征对(特征值和特征矢量),进而得到模态参数模型,即系统的模态频率、模态矢量、模态阻尼比、模态质量、模态刚度等参数。
特征根问题以图3所示的三自由度无阻尼系统为例,设123m =m =m =m ,123k =k =k =k ,图 1 三自由度系统其齐次运动方程为:(8)其中分别为系统的质量矩阵和刚度矩阵,123m 00m 00m=0m 0=0m 000m 00m ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,11212221k -k 0k -k 0k=-k k +k -k =-k 2k -k 0-k k 0-k k ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦,则运动方程展开式为: ¨11¨22¨33z m 00k k 0z 00m 0z k 2k k z 000m 0k k z 0z ⎡⎤⎢⎥-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥+--=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦(9)定义主振型由于是无阻尼系统,因此系统守恒,系统存在振动主振型。
主振型意味着各物理坐标振动的相位角不是同相(相差0o )就是反相位(相差180o ),即同时达到平衡位置和最大位置。
主振型定义如下:()i ij ωt+i i sin ωt+=Im(e)φφi mi mi z =z z (10)其中为第i 阶频率下,各自有度的位移矢量,为第i 个特征矢量,表示第i 阶固有频率下的振型,i ω为第i 阶频率下的第i 个特征值,i φ为初始相位。
对于三自由度系统,在第i 阶频率下,等式可以写成1m1i 2m2i i i 3m3i z z z =z sin(ωt+)z z φ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦(11)mki z 表示第k 个自由度在第i 阶模态下的模态矩阵。
点,有图可知节点并不唯一,而且修改前后节点的位置未变。
对应尽可能避开结构振动的节点,以免给测量带来误差。
4.4试验模态分析
试验模态分析的目的是为了验证理论模态分析的正确性的基础上进行深入研究奠定基础。
4.4.1试验模态分析的理论基础阻1所以在进行模态实验为在理论模态分析
在物理坐标下,描述N自由度离散振动系统的运动微分方程为
阻】耕+【c】扛}+医】M=沙}(4.2)式中:【M]——质量矩阵(对称且正定),M∈R~,
【C】——阻尼矩阵,C∈R“”,
晖】——刚度矩阵(对称且正定或半正定),K∈R“”,
{x),{卦,{封——N维位移、速度和加速度响应向量,
{厂(r))——_N维激振力向量。
设系统的初始状态为零,对式(4.2)两边进行拉普拉斯变换可得
([Mls2“C]s+【K]){X0))=【Z(s)]{工0))={F0))式中的矩阵
【Z(s)]-([M]s2+[c]s+[K】)
反映了系统的动态特性,称为系统动态矩阵或广义阻抗矩阵,其逆阵
[日(5)】=[Z(s)】~=(【M]s2+【C]s+[K])。
1称为广义导纳矩阵,也就是传递函数矩阵。
由式(2.2)可知
{x(J))_【日0)】(F(J)}
在上式中.令S=joJ,即可得到系统在频域内输出和输入的关系式
{并(国)}=【日(脚)】(F(国))(4.3)(4.4)(4.5)(4.6)(4.7)
式中[H(co)】为频率响应函数矩阵。
[H(∞)】矩阵中第f行_,列的元素
%(叻2篇(48)表示仅在』坐标激振(其余坐标激振力为零)时,i坐标的响应与激振力之比。
在式(4.4)中令S=_,∞,可得阻抗矩阵
[z(∞)】=([K]一曲2【吖])+jco[C](4.9)它和导纳矩阵有类似式(4.5)的关系
[日(珊)]=[z(国)】~={(【置卜。
2[^卅)+jco[C】}1(4.10)对于一般机械、结构,假设矩阵[c]也对称,这样矩阵【z(∞)】对称,频率响应函数矩阵[日@)]也对称,故有
q(脚)=HⅣ(03)(4.11)上式反映了机械、结构频率响应有互易性,可作为频率响应测试精度的一项重要检验手段。
利用振型矩阵的加权正交条件,即
蛾n圳¨:{o,H9蛾n州。
,)-{?’H9(4.12)12
{中。
}7【^卅{中,)={’1{m。
}。
【置】{o,)={,’1(4.。
【“,,,2q1I疗,,r29
式中:{o。
)、砷,)_一第g、,阶特征向量(固有振型),
m.、kr——第,阶模态质量和模态刚度。
并设矩阵【C】也可由振型矩阵【叫对角化,那么可以对阻抗矩阵进行如下变换
=[中]。
【o]7“[置卜出2[盯】)+_,珊[C])【∞]【中】-1
=c。
,4Ⅱ、七一、]一∞2[、m,、]+-,国[、c一、]}c西,~。
.。
,,
『\]
=【中】。
lo|【叫“
式中:z,=(七,一∞2m,)+,珊c,,c,是第r阶模态阻尼。
由(4.9)、(4.10)式可以得到用模态参数表示的频率响应函数矩阵为
江苏大学硕士学位论文
[H(珊)】矩阵中第i行,列的元素为(4.14)
吲妒喜而暑‰㈣式中:功::生——第,阶模态频率,
m.
善,==_三L——第r阶模态阻尼比
2m,∞,
{中,}——第r阶模态振型。
不难发现,N自由度系统的频率响应等于N个单自由度系统的频率响应的线性迭加。
为了确定全部模态参数曲,、善,、{中,)p=l…2..N),实际上只需测量频率响应函数矩阵的一列或一行就行了。
4.4.2模态参数识别
由f4.15)式可知,当珊趋近于某阶模态的固有频率时,该模态起主导作用,称为主模态。
在主模态附近,其它模态影响较小。
若模态密度不很大,各阶模态比较远离,其余模态的频率响应函数值在该主模态附近很小,且曲线比较平坦,即几乎不随频率而变化,因此其余模态的影响可用一复常数,t来表示,对第,阶模态(4.15)式可近似表示成
日”(珊)。
而弭i1再丽丽+日c
=去[矿豢‰一,矿考‰J(4峋
2而I五【矿万话历F叫瓦‘再丐蕊万矛j¨’”’+H:+jH2
H,@)的实部和虚部可表示如下
蹦咖去l矿≤岳]+彬
㈣。
去[矿耘卜根据上面两式可以作出实频图4.19和虚频图4.20。
O
O
图4.19第,阶模态频率响应函数的实频图
图4.20第r阶模态频率响应函数的复频图下面就可进行模态参数的确定口],[3H。
1)固有频率的确定(4.17)(4.18)
从实频图可以看出,固有频率就是实频曲线与剩余惯性直线日?@)=Hf的交点所对应的09值。
另外一种方法是从虚频图来确定,此时珊=∞,,正好对应虚频曲线的峰值,因为峰值较尖,所以更容易确定固有频率。
2)阻尼比的确定
阻尼比系数可以由半功率带宽Aco来确定,由图4.19的实频曲线对69求导可得
ACa=钆一09。
(4.19)对于模态阻尼系统,其阻尼比系数为
善,:.竺:掣(4.20)
¨
2珊,2∞,、
3)确定模态振型
由(4.18)式知,对主模态而言(不计剩余模态),当∞=珊,时,
H:‘甜2q’2霸--1‘4’21’
分别测出车身上各点的日:∞)t『-1…2..161)值,则可得到第,阶摸态的振型系数向量:
{中,)_扣:洄=(Or)}
=归j(出=q)日二(珊=(-Or)’・・日js,(c02啡)j
一南‰%…‰}
H.22)对于第,阶模态,当采用逐点激励,单点响应时,一—乓为常数。
因此
2m,鲁山,
p,}=溉(co=(Or)}即可代表模态振型。
因为振型只反映振动形式,与振动大小无关。
故常取归一化后的振型向量,在此归一化的方法是对响应点归一化,即取中。
=1・那么
p,)=砩洄=cot)}
=一去‰中n…叫@23’
41模态质量和刚度的确定
当09=q时,考虑,点激励,i点响应的频率响应函数,其虚部可以由(4.21)式近似表示
37—————————_-__l-———————_———__——_——————__-__--————一一
咸‘m2q’2丽ml㈣1
中。
中。
‘
2m,毒q2
若取响应点i的频率响应函数,且对响应点归一化,则车架结构阻尼系统的第r阶模态质量m,可以表示为
卅r2币丽耘一25’应该指出,模态质量的数值与归一化的方法有关,不同的归一化方法将得到不同的模态质量。
第,阶模态刚度可由下式求出
k,=m,co;(4.26)至此已求出全部的模态参数。
4.4.3白车身模态试验
由上可知,传递函数矩阵的一列或一行都含有模态向量.通过传递函数的一列或一行识别复模态矢量和极点位置,进而可以确定模态参数。
本文采用锤击法依次单点激励、单点测响应的试验方案.对NJ6400轿车的白车身进行了模态试验分析。
在试验过程中,输入信号由型号为5210的力锤产生,力传感器的型号为YDL.12.5,响应信号由型号为BK4321的三向加速度传感器拾取,激励和响应信号经电荷放大器放大后输入SD380动态分析仪,输出频率响应函数和相干函数曲线。
这些曲线可以硬拷贝输出,也可经计算机系统中的STAR5.7结构分析软件分析后,得出车身结构的各阶固有频率和振型。
由于汽车所受边界非完全自由而受弱约束,但它所受的约束相对结构自身的刚度来说仍小得多,因此采用自由支撑也是适当的。
本试验采用气垫支撑,相当于给结构增加了柔软约束,刚体模态频率不再是零。
经测量,气垫支撑的固有频率为5Hz左右,远低于白车身的第一阶固有频率。
所以它对车身模态分析的影响很小,
可以忽略不计。
1.测试系统框图如图4.2l所示。
在测试过程中,由于车身上有些点不方便固定三向加速度传感器,因此采用拾振的加速度传感器固定不动.激励的力锤移动的方法进行测量。