第7章函数练习题(含答案)

1、已知某完全竞争行业中的单个厂商的短期成本函数为STC=0.1Q 3-2Q 2+15Q+10。

试求：（1）当市场上产品的价格为P=55时，厂商的短期均衡产量和利润；（2）当市场价格下降为多少时，厂商必须停产？（3）厂商的短期供给函数。

解答：（1）因为STC=0.1Q 3-2Q 2+15Q+10所以SMC=dQdSTC =0.3Q 3-4Q+15 根据完全竞争厂商实现利润最大化原则P=SMC ，且已知P=55，于是有：0.3Q 2-4Q+15=55整理得：0.3Q 2-4Q-40=0解得利润最大化的产量Q *=20（负值舍去了）以Q *=20代入利润等式有：=TR-STC=PQ-STC=（55×20）-（0.1×203-2×202+15×20+10）=1100-310=790即厂商短期均衡的产量Q *=20，利润л=790（2）当市场价格下降为P 小于平均可变成本AVC 即P ≤AVC 时，厂商必须停产。

而此时的价格P 必定小于最小的可变平均成本AVC 。

根据题意，有： AVC=QQ Q Q Q TVC 1521.023+-==0.1Q 2-2Q+15 令即有,0=dQ dAVC ：022.0=-=Q dQdAVC 解得 Q=10 且02.022 =dQAVC d 故Q=10时，AVC （Q ）达最小值。

以Q=10代入AVC （Q ）有：最小的可变平均成本AVC=0.1×102-2×10+15=5于是，当市场价格P5时，厂商必须停产。

（3）根据完全厂商短期实现利润最大化原则P=SMC ，有：0.3Q 2-4Q+15=p整理得 0.3Q 2-4Q+（15-P ）=0 解得6.0)15(2.1164P Q --±= 根据利润最大化的二阶条件C M R M '' 的要求，取解为： Q=6.022.14-+P考虑到该厂商在短期只有在P 时5≥才生产，而P ＜5时必定会停产，所以，该厂商的短期供给函数Q=f （P ）为： Q=6.022.14-+P ，P 5≥ Q=0 P ＜52、已知某完全竞争的成本不变行业中的单个厂商的长期总成本函数LTC=Q 3-12Q 2+40Q 。

第7章复习与思考题求f (X )= 0的零点就等价于求(x )的不动点，选择一个初始近似值X 0，将它代入X =「(X ) 的右端，可求得X 1 h%X °)，如此反复迭代有 X k 1 二(X k ), k =0,1,2,..., (X)称为迭代函数，如果对任何X 。

• [a,b]，由x k 卜h%x k ),k =0,1,2,...得到的序列〈X k 1有极限则称迭代方程收敛，且X* =®(x*)为®(X )的不动点 故称X k q 二(X k ), k =0,1,2,...为不动点迭代法。

5•什么是迭代法的收敛阶？如何衡量迭代法收敛的快慢？如何确定X k 1 二「(X k )(k =0,1,2,...)的收敛阶P219设迭代过程X k 1'h%X k )收敛于 (X)的根X*，如果当k > 时，迭代误差e k = x k - x *满足渐近关系式—t C,C =const 式 0 e/则称该迭代过程是 p 阶收敛的，特别点，当 p=1时称为线性收敛，P>1时称为超线性收敛， p=2时称为平方收敛。

以收敛阶的大小衡量收敛速度的快慢。

6•什么是求解f(x)=0的牛顿法？它是否总是收敛的？若 f(X*) =0，X*是单根，f 是光 滑，证明牛顿法是局部二阶收敛的。

牛顿法:当| f (X k )卜J 时收敛。

7•什么是弦截法？试从收敛阶及每步迭代计算量与牛顿法比较其差别。

在牛顿法的基础上使用 2点的的斜率代替一点的倒数求法。

就是弦截法。

收敛阶弦截法1.618小于牛顿法2 计算量弦截法 <牛顿法(减少了倒数的计算量)8•什么是解方程的抛物线法？在求多项式全部零点中是否优于牛顿法？ P229X-mX k 1 =X kf (X k ) f (X k )设已知方程f （x） = 0的三个近似根，X k，X k^，X k^2，以这三点为节点构造二次插值多项式p（x），并适当选取p2（x）的一个零点X k卅作为新近似根，这样确定的迭代过程称为抛物线法。

[7.5 第2课时 解直角三角形的应用]一、选择题1．在Rt △ABC 中，∠C ＝90°，∠B ＝35°，AB ＝7，则BC 的长为( ) A ．7sin35° B.7cos35°C ．7cos35°D ．7tan35°2．如图K －31－1，点A (3，t )在第一象限，OA 与x 轴所夹的锐角为α，tan α＝32，则t 等于( )图K －31－1A ．0.5B ．1.5C ．4.5D ．23．等腰三角形的顶角为120°，腰长为2 cm ，则它的底边长为链接听课例2归纳总结( )A. 3 cmB.4 33cmC ．2 cmD ．2 3 cm 4．如图K －31－2，⊙O 的直径AB ＝2，弦AC ＝1，点D 在⊙O 上，则∠D 的度数为( )图K－31－2A．30° B．45° C．60° D．75°5．如图K－31－3，在△ABC中，∠BAC＝90°，AB＝AC，D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为( )图K－31－3A.13B.2－1 C．2－ 3 D.14二、填空题6．如图K－31－4，在平面直角坐标系xOy中，O为坐标原点，点P的坐标为(5，12)，那么OP与x轴正半轴所夹的锐角为________．(精确到0.1°)图K－31－47．如图K－31－5，在菱形ABCD中，AC＝6，BD＝8，则sin∠ABC＝________．图K－31－58．如图K－31－6，在△ABC中，∠A＝30°，∠B＝45°，AC＝2 3，则AB的长为________．图K－31－69．2018·安徽四模如图K－31－7，在△ABC中，AB＝AC，AH⊥BC，垂足为H，如果AH ＝BC，那么tan∠BAH的值是________．图K －31－710．2017·黑龙江在△ABC 中，AB ＝12，AC ＝39，∠B ＝30°，则△ABC 的面积是________． 三、解答题11．2018·淮南模拟如图K －31－8，在△ABC 中，∠A ＝30°，cos B ＝45，AC ＝6 3.求AB 的长.链接听课例2归纳总结图K －31－812．如图K －31－9，在平面直角坐标系内，O 为原点，点A 的坐标为(10，0)，点B 在第一象限内，BO ＝5，sin ∠BOA ＝35.求：(1)点B 的坐标； (2)cos ∠BAO 的值．图K －31－913．2018·广安改编如图K －31－10，已知AB 是⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，连接AC ，CG 是⊙O 的弦，CG ⊥AB ，垂足为D .(1)求证：∠PCA ＝∠ABC ；(2)过点A 作AE ∥PC 交⊙O 于点E ，连接BE .若cos P ＝45，PC ＝10，求BE 的长．图K －31－10阅读理解在锐角三角形ABC 中，∠A ，∠B ，∠ACB 的对边分别是a ，b ，c .如图K －31－11所示，过点C 作CD ⊥AB 于点D ，则cos A ＝AD b，即AD ＝b cos A ，图K －31－11∴BD ＝c －AD ＝c －b cos A .在Rt △ADC 和Rt △BDC 中，有CD 2＝AC 2－AD 2＝BC 2－BD 2， ∴b 2－b 2cos 2A ＝a 2－(c －b cos A )2，整理，得a 2＝b 2＋c 2－2bc cos A ，(1)同理可得b 2＝a 2＋c 2－2ac cos B ，(2) c 2＝a 2＋b 2－2ab cos ∠ACB . (3)这个结论就是著名的余弦定理，在以上三个等式中有六个元素a ，b ，c ，∠A ，∠B ，∠ACB ，若已知其中的任意三个元素，可求出其余的另外三个元素．如：在锐角三角形ABC 中，∠A ，∠B ，∠C 的对边分别是a ，b ，c ，已知∠A ＝60°，b ＝3，c ＝6，则由(1)式可得a 2＝32＋62－2×3×6cos60°＝27， ∴a ＝3 3，则∠B ，∠C 可由式子(2)，(3)分别求出，在此略． 根据以上阅读理解，请你试着解决如下问题：已知锐角三角形ABC 的三边a ，b ，c (a ，b ，c 分别是∠A ，∠B ，∠C 的对边)分别是7，8，9，求∠A ，∠B ，∠C 的度数．(结果精确到1°)详解详析[课堂达标]1．[解析] C 在Rt △ABC 中，cos B ＝BCAB ，所以BC ＝AB ·cos B ＝7cos 35°.故选C .2．[解析] C 如图，过点A 作AB ⊥x 轴于点B.∵点A(3，t)在第一象限， ∴AB ＝t ，OB ＝3. 又∵tan α＝AB OB ＝t 3＝32，∴t ＝4.5. 故选C .3．[解析] D 如图，过点A 作AD ⊥BC 于点D ，则∠BAD ＝∠CAD ＝60°，BD ＝DC.∵AD ⊥BC ，∴∠B ＝30°.∵AB ＝2 cm ， ∴AD ＝1 cm ，BD ＝ 3 cm ， ∴BC ＝2 3 cm .故选D .4．[解析] C ∵AB 是⊙O 的直径，∴∠ACB ＝90°.∵AC ＝1，AB ＝2，∴sin ∠ABC ＝ACAB ＝12，∴∠ABC ＝30°，∠A ＝60°，∴∠D ＝60°，故选C . 5．[解析] A ∵在△ABC 中，∠BAC ＝90°，AB ＝AC ， ∴∠ABC ＝∠C ＝45°，BC ＝2AC. 又∵D 为边AC 的中点， ∴AD ＝DC ＝12AC.∵DE ⊥BC 于点E ， ∴∠CDE ＝∠C ＝45°， ∴DE ＝EC ＝22DC ＝24AC ， ∴tan ∠DBC ＝DEBE ＝24AC 2AC －24AC ＝13. 故选A .6．[答案] 67.4°[解析] 如图，过点P 作PA ⊥x 轴，垂足为A.由勾股定理，得OP ＝122＋52＝13，∴cos ∠POA ＝513，∴∠POA ≈67.4°.7．[答案] 2425[解析] 过点A 作AE ⊥BC ，垂足为E ，由AC ＝6，BD ＝8，根据勾股定理得AB ＝32＋42＝5，菱形ABCD 的面积＝12AC·BD＝BC·AE，即12×6×8＝5×AE ，得AE ＝245，所以sin ∠ABC＝AE AB ＝2455＝2425. 8．[答案] 3＋ 3[解析] 如图，过点C 作CD ⊥AB 于点D ，则∠ADC ＝∠BDC ＝90°. ∵∠B ＝45°，∴∠BCD ＝∠B ＝45°， ∴CD ＝BD.∵∠A ＝30°，AC ＝2 3， ∴CD ＝3， ∴BD ＝CD ＝ 3.由勾股定理，得AD ＝AC 2－CD 2＝3， ∴AB ＝AD ＋BD ＝3＋ 3.9．[答案] 12[解析] 设AH ＝BC ＝2x.∵AB ＝AC ，AH ⊥BC ，∴BH ＝CH ＝12BC ＝x ，∴tan ∠BAH ＝BH AH ＝x 2x ＝12.10．[答案] 21 3或15 3[解析] (1)当∠ACB 为锐角时，如图①，过点A 作AD ⊥BC ，垂足为D.在Rt △ABD 中，∵AB ＝12，∠B ＝30°， ∴AD ＝12AB ＝6，BD ＝AB·cos B ＝12×32＝6 3.在Rt △ACD 中，CD ＝AC 2－AD 2＝（39）2－62＝3， ∴BC ＝BD ＋CD ＝6 3＋3＝7 3， 则S △ABC ＝12BC·AD＝12×7 3×6＝21 3；(2)当∠ACB 为钝角时，如图②，过点A 作AD ⊥BC ，交BC 的延长线于点D.由(1)知，AD ＝6，BD ＝6 3，CD ＝3，则BC ＝BD －CD ＝5 3，∴S △ABC ＝12BC·AD＝12×5 3×6＝15 3.故答案为21 3或15 3.11．解：如图，过点C 作CD ⊥AB 于点D.∵∠A ＝30°，∴CD ＝12AC ＝3 3，AD ＝AC ·cos A ＝9.∵cos B ＝45，∴设BD ＝4x ，则BC ＝5x.由勾股定理，得CD ＝3x.由题意，得3x ＝3 3，解得x ＝3， ∴BD ＝4 3，∴AB ＝AD ＋BD ＝9＋4 3.12．解：(1)如图，过点B 作BH ⊥OA ，垂足为H.在Rt △OHB 中，∵BO ＝5，sin ∠BOA ＝35，∴BH ＝BO·sin ∠BOA ＝5×35＝3，∴OH ＝BO 2－BH 2＝4， ∴点B 的坐标为(4，3)．(2)∵OA ＝10，OH ＝4，∴AH ＝6. 在Rt △AHB 中， ∵BH ＝3，AH ＝6， ∴AB ＝BH 2＋AH 2＝3 5， ∴cos ∠BAO ＝AH AB ＝2 55.13．解：(1)证明：连接OC.∵PC 与⊙O 相切于点C ，∴∠PCO ＝90°，∴∠PCA ＋∠OCA ＝90°. ∵AB 是⊙O 的直径，∴∠ACB ＝90°， ∴∠OCB ＋∠OCA ＝90°， ∴∠PCA ＝∠OCB.∵OC ＝OB ，∴∠OCB ＝∠ABC ， ∴∠PCA ＝∠ABC.(2)∵cos P ＝PC OP ＝45，PC ＝10，∴OP ＝252，∴OC ＝OP 2－CP 2＝152，∴AB ＝15.∵AE ∥PC ，∴∠BAE ＝∠P.∵AB 是⊙O 的直径，∴∠E ＝90°， ∴AE ＝AB·cos ∠BAE ＝15×45＝12，∴BE ＝AB 2－AE 2＝9. [素养提升][解析] 此题只要把三边长代入余弦定理公式即可求出三角的余弦值，从而求出三角．解：由(1)得72＝82＋92－2×8×9cos A ， 则cos A ＝23，∠A ≈48°.由(2)得82＝72＋92－2×7×9cos B ， 则cos B ＝1121，∠B ≈58°，∴∠C ＝180°－∠A －∠B ≈74°.。

第一章函数与极限一、选择题：1．函数的定义域是（）(A； (B； (C；(D.2.函数的定义域是（）(A；(B;(C;(D.3、函数是（）(A偶函数； (B奇函数；(C非奇非偶函数；(D奇偶函数.4、函数的最小正周期是（）(A2； (B； (C 4 ； (D .5、函数在定义域为（）(A有上界无下界； (B有下界无上界；(C有界，且；(D有界，且.6、与等价的函数是（）(A ； (B ； (C ； (D .7、当时，下列函数哪一个是其它三个的高阶无穷小（）（A）；（B）；（C）；（D）.8、设则当（）时有.(A； (B；(C； (D任意取 .9、设,则((A-1 ； (B1 ； (C0 ； (D不存在 .10、（）(A1； (B-1；(C0； (D不存在.二、求下列函数的定义域：2、 .三、设（1）试确定的值使；（2）求的表达式 .四、求的反函数.五、求极限：1、；2、；3、；4、；5、当时，；6、 .六、设有函数试确定的值使在连续 .七、讨论函数的连续性，并判断其间断点的类型 .八、证明奇次多项式：至少存在一个实根 .第二章导数与微分一、选择题：1、函数在点的导数定义为（）（A）；（B）；（C）；（D）；2、若函数在点处的导数，则曲线在点(处的法线（）（A）与轴相平行；（B）与轴垂直；（C）与轴相垂直；（D）与轴即不平行也不垂直：3、若函数在点不连续，则在 (（A）必不可导；（B）必定可导；（C）不一定可导；（D）必无定义.4、如果=（），那么.(A ；(B ；(C ；(D .5、如果处处可导，那末（）（A）；（B）；（C）；（D）.6、已知函数具有任意阶导数，且,则当为大于2的正整数时，的n阶导数是（）（A）；（B）；（C）；（D）.7、若函数,对可导且,又的反函数存在且可导，则=（）（A）；（B）；（C）；（D）.8、若函数为可微函数，则（）（A）与无关；（B）为的线性函数；（C）当时为的高阶无穷小；（D）与为等价无穷小.9、设函数在点处可导，当自变量由增加到时，记为的增量，为的微分，等于（）（A）-1；（B）0；（C）1；（D）.10、设函数在点处可导，且，则等于（）.（A）0；（B）-1；（C）1；（D） .二、求下列函数的导数：1、；2、（）；3、；4、；5、设为的函数是由方程确定的；6、设，，求.三、证明，满足方程.四、已知其中有二阶连续导数，且，1、确定的值，使在点连续；2、求五、设求.六、计算的近似值 .七、一人走过一桥之速率为4公里/小时，同时一船在此人底下以8公里/小时之速率划过，此桥比船高200米，问3分钟后人与船相离之速率为多少？第三章微分中值定理一、选择题：1、一元函数微分学的三个中值定理的结论都有一个共同点，即（）（A）它们都给出了ξ点的求法 .（B）它们都肯定了ξ点一定存在，且给出了求ξ的方法。

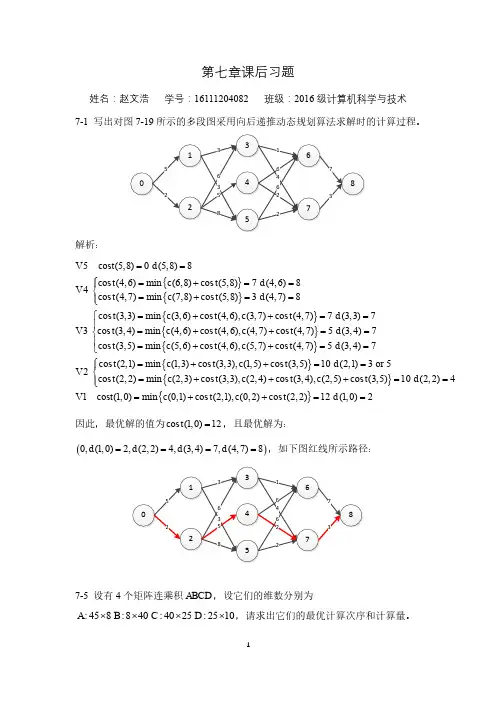
7-1.字典方法。

哪个字典方法可以用来把两个字典合并到一起。

答案：dict.update(dict2)将字典dict2的键-值对添加到字典dict中7-2.字典的键。

我们知道字典的值可以是任意的Python对象，那字典的键又如何呢？请试着将除数字和字符串意外的其他不同类型的对象作为字典的键，看看哪些类型可以，哪些不行。

对那些不能作为字典的键的对象类型，你认为是什么原因呢？答案：键必须是可哈希的。

所有不可变的类型都是可哈希的，因此他们都可以作为字典的键。

一个要说明的问题是：值相等的数字表示相同的键。

换句话说，整型数字1和浮点型1.0的哈希值是相同的，即它们是相同的键。

同时，也有一些可变对象(很少)是可哈希的，它们可以作为字典的键，但很少见。

用元组做有效的键，必须要加限制：元组中只包括像数字和字符串这样的不可变参数，才可以作为字典中有效的键。

内建函数hash()可以判断某个对象是否可以做一个字典的键，如果非可哈希类型作为参数传递给hash()方法，会产生TypeError错误，否则会产生hash值，整数。

>>> hash(1)1>>> hash('a')-468864544>>> hash([1,2])Traceback (most recent call last):File "<pyshell#2>", line 1, in <module>hash([1,2])TypeError: unhashable type: 'list'>>> hash({1:2,})Traceback (most recent call last):File "<pyshell#3>", line 1, in <module>hash({1:2,})TypeError: unhashable type: 'dict'>>> hash(set('abc'))Traceback (most recent call last):File "<pyshell#4>", line 1, in <module>hash(set('abc'))TypeError: unhashable type: 'set'>>> hash(('abc'))-1600925533>>> hash(1.0)1>>> hash(frozenset('abc'))-114069471>>> hash(((1,3,9)))1140186820>>> hash(((1,3,9),(1,2)))340745663>>> hash(((1,3,'9'),(1,2)))1944127872>>> hash(((1,3,'9'),[1,2],(1,2)))Traceback (most recent call last):File "<pyshell#11>", line 1, in <module>hash(((1,3,'9'),[1,2],(1,2)))TypeError: unhashable type: 'list'>>>7-3.字典和列表的方法。

第7章习题：1.设A={0,1}，试给出半群<A A,︒>的运算表，其中︒为函数的复合运算。

2.S={a,b,c}，*是S上的二元运算，且∀x,y∈S, x *y = x(1) 证明S关于*运算构成半群；(2) 试通过增加最少的元素使得S扩张成一个独异点。

3.给定代数结构〈R,∗〉，其中R是实数集合，对R中任意元a和b，∗定义如下：a∗b=a+b+ab试证：〈R,∗〉是独异点。

4.给定半群〈S,∗〉,a∈S,对于S中的任意元x和y,定义二元运算如下：x⊕y=x∗a∗y试证：〈R,⊕〉是半群。

5.指出下述各代数系统哪些是半群，并说明理由。

（1）[Z;−]。

（2）[C;×]。

（3）[M m,n(Q);+]。

（4）[Z n;⊕]，⊕为同余类的加法运算。

6.设V=<{a,b},*>是半群，且a*a=b，证明：(1) a*b=b*a(2) b*b=b7.S={a,b,c},∗是S上的二元运算，且∀x ,y∈S,x∗y=x.（1）证明S关于∗运算构成半群。

（2）试通过增加最少的元素使得S扩张成一个独异点。

8.设Z为整数集合，在Z上定义二元运算︒如下：∀x,y∈Z，x︒y=x+y-2问Z关于︒运算能否构成群？为什么？9.设A={x|x∈R∧x≠0,1} ，在A上定义6个函数如下：f1(x)=x; f2(x)=x-1; f3(x)=1-x;f4(x)=(1-x)-1; f5(x)=(x-1)x-1; f6(x)=x(x-1)-1令F为这6个函数构成的集合，︒运算为函数的复合运算，(1) 给出︒运算的运算表(2) 验证<F, ︒>是一个群10.判断下列集合关于指定的运算是否构成半群，独异点和群。

（1）a是正实数，G={a n|n∈Z}，运算是普通乘法。

（2）Q+为正有理数，运算是普通乘法。

（3）Q+为正有理数，运算是普通加法。

（4）一元实系数多项式的集合关于多项式的乘法。

第七章线性变换1．判别下面所定义的变换那些是线性的，那些不是：1）在线性空间V中，A,其中V是一固定的向量；2）在线性空间V中，A其中V是一固定的向量；3）在P 322 中，A(,,)(,,)x1xxxxxx；2312334）在P 3中，A(,,)(2,,)x1xxxxxxx2312231；5）在P[x]中，A f(x)f(x1)；6）在P[x]中，A()(),fxfx其中0 x P是一固定的数；07）把复数域上看作复数域上的线性空间，A。

nn中，A X=BXC其中B,CP 8）在P解1)当0时,是;当0时,不是。

nn是两个固定的矩阵.2)当0时,是;当0时,不是。

3)不是.例如当(1,0,0),k2时,k A()(2,0,0),A(k)(4,0,0), A(k)k A()。

4)是.因取(x1,x2,x3),(y1,y2,y3),有A()=A(x1y1,x2y2,x3y3)=(2x12y1x2y2,x2y2x3y3,x1y1)=(2x1x2,x2x3,x1)(2y1y2,y2y3,y1)=A+A，A(k)A(kx1,kx2,kx3)(2kx1 k x2,k x2k x,3k x)1(2kx1 k x2,k x2k x,3k x)1=k A()，3故A是P上的线性变换。

5)是.因任取f(x)P[x],g(x)P[x],并令u(x)f(x)g(x)则A(f(x)g(x))=A u(x)=u(x1)=f(x1)g(x1)=A f(x)+A(g(x))，再令v(x)kf(x)则A(kf(x))A(v(x))v(x1)kf(x1)k A(f(x))，故A为P[x]上的线性变换。

6)是.因任取f(x)P[x],g(x)P[x]则.A(f(x)g(x))=f(x0)g(x0)A(f(x))A(g(x))，A(kf(x))kf(x0)k A(f(x))。

7)不是，例如取a=1,k=I，则A(ka)=-i,k(A a)=i,A(ka)k A(a)。

第7章综合素质评价一、选择题(每题3分，共24分)1．sin 30°的值等于()A．12B．22C．32D．332．【母题：教材P 102例3】如图，在Rt△ABC 中，∠C ＝90°，BC ＝4，AB ＝5，则sin A 的值为()A．35B．53C．45D．343．【2023·益阳一中月考】已知α为锐角，且sin α＝32，则α的度数为()A．30°B．60°C．45°D．75°4．【2023·苏州中学月考】化简(sin 28°－cos 28°)2等于()A．sin 28°－cos 28°B．0C．cos 28°－sin 28°D．以上都不对5．【2023·长春】学校开放日即将来临，负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB 到地面，如图所示，已知彩旗绳与地面形成25°角(即∠BAC ＝25°)，彩旗绳固定在地面的位置与图书馆相距32m(即AC ＝32m)，则彩旗绳AB 的长度为()A．32sin 25°mB．32cos 25°mC．32sin 25°mD．32cos 25°m6．【2022·贵港】如图，某数学兴趣小组测量一棵树CD 的高度，在点A 处测得树顶C 的仰角为45°，在点B 处测得树顶C 的仰角为60°，且A ，B ，D 三点在同一直线上，若AB ＝16m，则这棵树CD 的高度是()A．8(3－3)m B．8(3＋3)m C．6(3－3)m D．6(3＋3)m 7．【2023·连云港新区新海实验中学月考】如图，E 是菱形ABCD 的边BC 上的点，连接AE .将菱形ABCD 沿AE 翻折，点B 恰好落在CD 的中点F 处，则tan∠ABE 的值是()A．4B．5C．13D．158．【2023·扬州仪征一模】如图，△ABC 中，∠B ＝90°，tan A ＝12，点D 是AB 的中点，点E 在线段AC 上运动(不与点A ，C 重合)，若AD AB ＝DE BC ，则AEAC的值为()A．12或310B．12C．12或14D．12或58二、填空题(每题3分，共30分)9．如图，在Rt△ABC 中，∠C ＝90°，AB ＝13，AC ＝5，则cos A 的值是________．10．如图，点A (3，t )在第一象限，OA 与x 轴所夹的锐角为α，tan α＝32，则t的值是________．11．【2022·柳州】如图，某水库堤坝横断面迎水坡的坡角为α，sin α＝35，堤坝高BC ＝30m，则迎水坡坡面AB 的长度为________m.12．【2023·永州四中月考】如图，已知正方形ABCD 的边长为2，如果将线段BD 绕着点B 旋转后，点D 落在CB 延长线上的D ′处，那么tan∠BAD ′＝________.13．【2023·常州实验中学一模】如图，在矩形ABCD 中，E 为AD 上的点，AE ＝AB ，BE ＝DE ，则tan∠BDE ＝________.14．【母题：教材P 112习题T 4】如图，在菱形ABCD 中，对角线AC ，BD 相交于点O ，BD ＝8，tan∠ABD ＝34，则线段AB 的长为________．15．如图，由小正方形组成的网格中，点A ，B ，C 都在格点上，点D 不在格点上，以AB 为直径的圆经过点C 和点D ，则∠BDC 的正切值是________．16．【2023·广西】如图，焊接一个钢架，包括底角为37°的等腰三角形外框和3m 高的支柱，则共需钢材约________m(结果取整数)．(参考数据：sin 37°≈0.60，cos 37°≈0.80，tan 37°≈0.75)17．【2023·枣庄】如图所示，桔槔是一种原始的汲水工具，它是在一根竖立的架子上加上一根细长的杠杆，末端悬挂一重物，前端悬挂水桶，当人把水桶放入水中打满水以后，由于杠杆末端的重力作用，便能轻易把水提升至所需处，若已知：杠杆AB ＝6米，AO ：OB ＝2：1，支架OM ⊥EF ，OM ＝3米，AB 可以绕着点O 自由旋转，当点A 旋转到如图所示位置时∠AOM ＝45°，此时点B 到水平地面EF 的距离为________米．(结果保留根号)18.如图，将Rt△ABC 沿斜边AB 翻折得到△ABD ，O 为斜边AB 的中点，连接DO 并延长DO 使DO ＝OE ，连接AE ，已知AC ＝9，BC ＝3，则cos∠CAE ＝________.三、解答题(19～22题每题6分，23题8分，24题10分，25～26题每题12分，共66分)19．【母题：教材P 106习题T 1】计算：(1)2cos 30°－tan 60°＋sin 45°cos 45°；(2)3－(π－3)0－10sin 30°＋12－2.20．【母题：教材P119复习题T5】在△ABC中，∠C＝90°，∠A，∠B，∠C所对的边分别为a，b，c.(1)已知c＝2，∠A＝60°，求∠B，a，b；(2)已知a＝2，∠A＝45°，求∠B，b，c.21．【2023·邵阳五中月考】如图，△ABC中，∠A＝30°，AC＝23，tan B＝32，求AB的长．22．【2023·无锡锡山高级中学月考】如图，矩形ABCD中，AB＝4，BC＝5，E是CD边上的一点，点P在BC边上，且满足∠PEC＝∠DAP.(1)请用不带刻度的直尺和圆规，在所给的图中作出符合条件的点P；(不要求写作法，但保留作图痕迹)(2)若CE＝1，试确定tan∠EPC的值．23．【2023·内蒙古】为了增强学生体质、锤炼学生意志，某校组织一次定向越野拉练活动．如图，A点为出发点，途中设置两个检查点，分别为B点和C点，行进路线为A→B→C→A，B点在A点的南偏东25°方向32km处，C点在A点的北偏东80°方向，行进路线AB和BC所在直线的夹角∠ABC为45°.(1)求行进路线BC和CA所在直线的夹角∠BCA的度数；(2)求检查点B和C之间的距离(结果保留根号)．24．【2023·扬州】如图，在△ABC中，∠ACB＝90°，点D是AB上一点，且∠BCD＝1 2∠A，点O在BC上，以点O为圆心的圆经过C，D两点．(1)试判断直线AB与⊙O的位置关系，并说明理由；(2)若sin B＝35，⊙O的半径为3，求AC的长．25.多边形面积的求解有多种方法，通过不同方法的应用，可以求解某些边和角．【基础掌握】(1)在▱ABCD中，∠A＝60°，AB＝8，AD＝6.求▱ABCD的面积；【灵活运用】(2)在△ABC中，AB＝20，AC＝15，sin B＝35，求△ABC的面积．【迁移提升】(3)如图，△ABC的顶点都在边长为1的正方形的顶点上，请直接写出sin B的值．26.如图，在平面直角坐标系中，直线y＝－43x＋4与x轴，y轴分别交于B，C两点，抛物线y＝ax2＋bx＋c经过B，C两点，与x轴负半轴交于点A，连接AC，且cos∠CAB＝17 17.(1)求抛物线表达式；(2)点P是抛物线上的一点．当点P在第一象限时，过点P作PD∥y轴交BC于点D，过点D作DE⊥y轴于点E，连接EP，当△PDE和△BOC相似时，求点P的坐标．答案一、1．A 2．C【点拨】由题意可知，∠C ＝90°，因为AB ＝5，BC ＝4，所以sin A ＝BC AB ＝45.3．B 4．C5．D 【点拨】如图，由题意得，AC ＝32m，∠BAC ＝25°，BC ⊥AC .在Rt△ABC 中，∵cos∠BAC ＝AC AB ，∴AB ＝AC cos∠BAC ＝32cos 25°m，故选D.6．A【点拨】设CD ＝x m，在Rt△ADC 中，∠A ＝45°，∴CD ＝AD ＝x m．∴BD ＝(16－x )m.在Rt△BCD 中，∠B ＝60°，∴tan B ＝CD BD ，即x16－x ＝3，解得x ＝8(3－3)．故选A.7．D【点拨】过点A 作AN ⊥DF 于点N ，如图．∵四边形ABCD 是菱形，∴AB ＝CD ＝AD ，∠ABE ＝∠D .设AD ＝4.∵F 是CD 的中点，∴DF ＝FC ＝2.根据翻折的性质可知AB ＝AF ，∴△AFD 是等腰三角形．∵AN ⊥DF ，∴DN ＝NF ＝1.∴在Rt△AND 中，AN ＝AD 2－DN 2＝42－12＝15.∴tan D ＝AN ND ＝151＝15.∴tan∠ABE ＝15.故选D.8．A【点拨】∵D 为AB 的中点，AD AB ＝DE BC ＝12，∴DE ＝12BC .如图，取AC 的中点E 1，连接DE 1，则DE 1是△ABC 的中位线，此时DE 1∥BC ，DE 1＝12BC ，∴AE 1AC ＝12.如图，在AC 上取一点E 2，使得DE 1＝DE 2，则△DE 1E 2是等腰三角形，过点D 作DM ⊥AC ，则ME 1＝ME 2，∠MDE 1＋∠ME 1D ＝90°.∵∠B ＝90°，DE 1∥BC ，∴∠ADE 1＝90°.∴∠A ＋∠AE 1D ＝90°.∴∠A ＝∠MDE 1.∵tan A ＝12，∴tan∠MDE 1＝12.设ME 1＝ME 2＝x ，则DM ＝2x ，∴DE 1＝DE 2＝5x ，E 1E 2＝2x .∵DE 1＝12BC ，∴BC ＝25x .∵tan A ＝12，∴AB ＝45x .∴AC ＝10x .∵AE 1AC ＝12，∴AE 1＝5x .∴AE 2＝AE 1－E 1E 2＝5x －2x ＝3x .∴AE 2AC ＝3x 10x ＝310.综上，AE AC 的值为12或310.故选A.1111二、9．51310．92【点拨】如图，过点A 作AB ⊥x 轴于点B .∵点A (3，t )在第一象限，∴AB ＝t ，OB ＝3.∴tan α＝AB OB ＝t 3＝32.∴t ＝92.11．50【点拨】根据题意得∠ACB ＝90°，sin α＝35，∴BC AB ＝35.∵BC ＝30m，∴30AB＝35，解得AB ＝50m，即迎水坡坡面AB 的长度为50m.12．213．2－1【点拨】设AB ＝1，∵在矩形ABCD 中，E 为AD 上的点，AE ＝AB ，BE ＝DE ，∴ED ＝BE ＝AE 2＋AB 2＝ 2.∴AD ＝AE ＋ED ＝1＋ 2.∴tan∠BDE ＝AB AD ＝11＋2＝2－1.故答案为2－1.14．5【点拨】∵四边形ABCD 是菱形，∴AC ⊥BD ，OB ＝OD .∴∠AOB ＝90°.∵BD ＝8，∴OB ＝4.∵tan∠ABD ＝34＝AO OB ，∴AO ＝3.在Rt△AOB 中，由勾股定理得AB ＝AO 2＋OB 2＝32＋42＝5.15．23【点拨】∵AB 为圆的直径，∴∠ACB ＝90°.∵∠BDC ＝∠BAC ，∴tan∠BDC ＝tan∠BAC .∵在Rt△ACB 中，tan∠BAC ＝BC AC ＝23，1212∴tan∠BDC ＝23.16．21【点拨】∵CA ＝CB ，CD ⊥AB ，∴AD ＝BD ＝12AB .在Rt△ACD 中，∠CAD ＝37°，CD ＝3m，∴AC ＝CDsin 37°≈30.6＝5(m)，AD ＝CDtan 37°≈30.75＝4(m)，∴CA ＝CB ≈5m，AB ＝2AD ≈8(m)，∴AC ＋CB ＋AB ＋CD ≈5＋5＋8＋3＝21(m)．∴共需钢材约21m.17．(3＋2)【点拨】如图，过点O 作OC⊥BT ，垂足为C .由题意得BC ∥OM ，∴∠AOM ＝∠OBC ＝45°.∵AB ＝6米，AO ：OB ＝2：1，∴AO ＝4米，OB ＝2米，在Rt△OBC 中，BC ＝OB ·cos 45°＝2×22＝2(米)．∵OM ＝3米，∴此时点B 到水平地面EF 的距离为BC ＋OM ＝(3＋2)米．18．35【点拨】如图，连接BE 交AC 于点F ，在四边形ADBE 中，∵O 为AB 的中点，DO ＝OE ，1313∴四边形ADBE 是平行四边形．又∵Rt△ABC 沿斜边AB 翻折得到△ABD ，∴∠ADB ＝∠C ＝90°.∴四边形ADBE 是矩形．∴∠AEF ＝90°，AE ＝BD .又∵Rt△ABC 沿斜边AB 翻折得到△ABD ，∴AE ＝BD ＝BC ＝3.∵∠AEF ＝∠C ＝90°，∠AFE ＝∠BFC ，AE ＝BC ，∴△AEF ≌△BCF (AAS)，∴AF ＝BF .设AF ＝BF ＝x ，则CF ＝9－x ，在Rt△FBC 中，FB 2＝CF 2＋BC 2，∴x 2＝(9－x )2＋32，解得x ＝5.∴AF ＝5.∴cos∠CAE ＝AE AF ＝35.故答案为35.三、19．【解】(1)原式＝2×32－3＋22×22＝3－3＋12＝12.(2)原式＝3－1－10×12＋4＝3－1－5＋4＝3－2.20．【解】(1)∠B ＝90°－∠A ＝30°.∵sin B ＝bc ，∴b ＝c ·sin B ＝2·sin 30°＝1.∵cos B ＝ac ，∴a ＝c ·cos B ＝2·cos 30°＝ 3.(2)∠B ＝90°－∠A ＝45°.∵tan A ＝ab ，∴b ＝atan A ＝2tan 45°＝ 2.∵sin A ＝ac ，∴c ＝a sin A ＝2sin 45°＝222＝2.21．【解】过C 点作CD ⊥AB 于D ，如图．在Rt△ACD 中，∵sin A ＝CDAC ，cos A ＝ADAC ，∴sin 30°＝CD 23，cos 30°＝AD23.1414∴CD ＝12×23＝3，AD ＝32×23＝3.在Rt△BCD 中，∵tan B ＝CD BD，∴BD ＝CD tan B ＝332＝2.∴AB ＝AD ＋BD ＝3＋2＝5.22．【解】(1)如图，连接AE ，作AE 的垂直平分线，以AE 为直径画圆，交BC 于点P′和P ″，则∠AP ′E ＝∠AP ″E ＝90°.∵∠P ′EC ＋∠P ′ED ＝180°，∠P ′AD ＋∠P ′ED ＝360°－90°－90°＝180°，∴∠P ′EC ＝∠DAP ′.同理可得∠P ″EC ＝∠DAP ″.则点P ′和P ″即为所求．(2)∵在矩形ABCD 中，AD ∥BC ，∴∠DAP ＝∠APB .∵∠PEC ＝∠DAP ，∴∠APB ＝∠PEC .∵∠B ＝∠C ＝90°，∴△ABP ∽△PCE .∴BPCE ＝ABPC .设PC ＝x ，∵BC ＝5，∴BP ＝5－x .∴5－x 1＝4x ，解得x 1＝1，x 2＝4，∴PC 的长为1或4.当PC ＝1时，tan∠EPC ＝CE CP ＝11＝1，当PC ＝4时，tan∠EPC ＝CE CP ＝14.23．【解】(1)由题意得∠NAC ＝80°，∠BAS ＝25°，∴∠CAB ＝180°－∠NAC －∠BAS ＝75°.∵∠ABC ＝45°，∴∠BCA ＝180°－∠CAB －∠ABC ＝60°，1515∴行进路线BC 和CA 所在直线的夹角∠BCA 的度数为60°.(2)如图，过点A 作AD ⊥BC ，垂足为D，在Rt△ABD 中，AB ＝32km，∠ABC ＝45°，∴AD ＝AB ·sin 45°＝32×22＝3(km)，BD ＝AB ·cos 45°＝32×22＝3(km)，在Rt△ADC 中，∠BCA ＝60°，∴CD ＝AD tan 60°＝33＝3(km)，∴BC ＝BD ＋CD＝(3＋3)km，∴检查点B 和C 之间的距离为(3＋3)km.24．【解】(1)直线AB 与⊙O 相切．理由：如图，连接OD .∵OC ＝OD ，∴∠OCD ＝∠ODC ，∴∠DOB ＝∠OCD ＋∠ODC ＝2∠BCD ，∴∠BCD ＝12∠BOD .∵∠BCD ＝12∠A ，∴∠BOD ＝∠A .∵∠ACB ＝90°，∴∠A ＋∠B ＝90°，∴∠BOD ＋∠B ＝90°，∴∠BDO ＝90°，∴OD ⊥AB .又∵OD 是⊙O 的半径，∴直线AB 与⊙O 相切．1616(2)∵sin B ＝OD OB ＝35，OD ＝3，∴OB ＝5，∴BC ＝OB ＋OC ＝8.在Rt△ACB 中，∵sin B ＝AC AB ＝35，∴设AC ＝3x ，则AB ＝5x ，∴BC ＝AB 2－AC 2＝4x ＝8，∴x ＝2，∴AC ＝3x ＝6.25．【解】(1)如图①.过点B 作BE ⊥AD 于点E ，∵∠A ＝60°，AB ＝8，∴BE ＝AB ·sin A ＝8×32＝4 3.∵AD ＝6，∴▱ABCD 的面积＝AD ·BE ＝6×43＝24 3.(2)如图②，过点A 作AD ⊥BC 于点D ，则AD ＝AB ·sin B ＝20×35＝12.∴BD ＝AB 2－AD 2＝202－122＝16，CD ＝AC 2－AD 2＝152－122＝9.∴BC ＝BD ＋CD ＝16＋9＝25.∴△ABC 的面积＝12BC ·AD ＝12×25×12＝150.(3)sin B ＝78585.【点拨】设△ABC 底边BC 上的高为h ，则h ＝AB ·sin B ，1717∴S △ABC ＝12·h ·BC ＝12·AB ·BC ·sin B .由题意知，AB ＝22＋42＝25，BC ＝12＋42＝17.∵S △ABC ＝4×4－12×2×4－12×2×3－12×1×4＝7.∴sin B ＝2×725×17＝78585.26．【解】(1)∵直线y ＝－43x ＋4与x 轴，y 轴分别交于B ，C 两点，当x ＝0时，y ＝－43×0＋4＝4，当y ＝0时，－43x ＋4＝0，解得x ＝3，∴C (0，4)，OC ＝4，B (3，0)，OB ＝3.在Rt△AOC 中，cos∠CAB ＝OAAC ＝1717，设OA ＝17k ，则AC ＝17k .∵AC 2＝OA 2＋OC 2，∴(17k )2＝(17k )2＋42，解得k 1＝1717，k 2＝－1717(舍去)，∴OA ＝17k ＝1，∴A (－1，0)．∵抛物线y ＝ax2＋bx ＋c 经过B ，C 两点，与x 轴负半轴交于点A ，－b ＋c ＝0，a ＋3b ＋c ＝0，＝4，＝－43，＝83，＝4.∴抛物线的表达式为y ＝－43x 2＋83x ＋4.(2)设P，－43m 2＋83m∵PD ∥y 轴交BC 于点D ，DE ⊥y轴于点E ，∴，－43m ∴PD ＝－43m 2＋83m －43m ＝－43m 2＋4m ，DE ＝m .∴tan∠PED ＝PDDE ＝－43m ＋4.∵∠PDE ＝∠BOC ＝90°，∴△PDE 和△BOC 相似分以下两种情况：当∠PED ＝∠CBO 时，tan∠PED＝tan∠CBO＝CO BO ，∴－43m＋4＝43，解得m＝2.∴－43m2＋83m＋4＝－43×22＋83×2＋4＝4.∴P(2，4)；当∠PED＝∠BCO时，tan∠PED＝tan∠BCO＝BO CO ，∴－43m＋4＝34，解得m＝3916.∴－43m2＋83m＋4＝－43×＋83×3916＋4＝16564.∴综上所述，当△PDE和△BOC相似时，点P1818。

复习与思考题1.什么是方程的有根区间？它与求根有何关系?P213，若f(x)€C［a,b］且f(a)f(b) c O，根据连续函数性质可知f(x) = O在［a,b］内至少有一个实根，这时称［a,b］为f(x)=O的有根区间。

2.什么是二分法？用二分法求f(x)=O的根，f要满足什么条件?P213般地，对于函数f(x)=O如果存在实数C,当x=c时，若f(c)=O,那么把x=c叫做函数f(x)=O的零点。

解方程即要求f(X)=0的所有零点。

假定f(X)=0在区间(X, y)上连续, 先找到a、b属于区间(x，y)，使f(a)f(b) cO，说明在区间(a,b)内一定有零点，然后求f((a + b)/2)，现在假设f(a) <O, f(b) AO,acb果f((a + b)/2)=O，该点就是零点，如果f((a + b)/2)< O则在区间［(a + b)/2),b］内有零点，从①开始继续使用中点函数值判断。

如果f((a + b)/2) AO，则在区间［a,(a+b)/2)］内有零点，从①开始继续使用中点函数值判断。

这样就可以不断接近零点。

通过每次把f(x)的零点所在小区间收缩一半的方法，使区间的两个端点逐步迫近函数的零点，以求得零点的近似值，这种方法叫做二分法。

从以上可以看出，每次运算后，区间长度减少一半，是线形收敛。

3.什么是函数W(x) =O的不动点？如何确定®(x)使它的不动点等价于f(x)的零点P 215.将方程f(x)=O改写成等价的形式x=W(x)，若要求X*满足f(x*) = O,贝y x*=W(x*)；反之亦然，称x*为函数申(x)的一个不动点。

4.什么是不动点迭代法？申(X)满足什么条件才能保证不动点存在和不动点迭代序列收敛于④(X)的不动点P 215求f(x)=0的零点就等价于求W (x)的不动点，选择一个初始近似值x0，将它代入x N (x) 的右端，可求得X i =9(X 0)，如此反复迭代有 Xk+ =^(X k ),k =0,1,2,..., ®(x)称为迭代函数，如果对任何x^<^[a,b]，由兀屮=w (x k ),k =0,1,2,...得到的序列 {xk }有极限kim X k =x* ，则称迭代方程收敛，且X* =^(x*)为甲(X)的不动点，故称Xk+ =®(X k ),k =0,1,2,...为不动点迭代法。

p317第七章习题(一) [ 2, 5, 6, 9, 15, 17, 19 ]2. 利用保域定理证明：若函数f(z)在区域D内解析，(1) 若| f(z) |在D内为常数，则f(z)在D内为常数；(2) 若Re( f(z))或Im( f(z))在D内为常数，则f(z)在D内为常数．【解】由保域定理，假若f(z)在区域D内不恒为常数，则f(D)是区域．(1) 若| f(z) |在D内为常数，则存在r ≥ 0，使得f(D) ⊆C r= { z∈ | | z | = r }．但int(C r) = ∅，故int( f(D)) = ∅，因此f(D)不是开集，因此不是区域，矛盾．(2) 若Re( f(z))在D内为常数，则存在a∈ ，使得f(D) ⊆L a= { z∈ | Re(z) = a }．但int(L a) = ∅，故int( f(D)) = ∅，因此f(D)不是开集，因此不是区域，矛盾．同理，若Im( f(z))在D内为常数，f(D)也不是区域，矛盾．故不论如何，f(z)在区域D内必恒为常数．[保区域性定理：设f(z)在区域D内解析且不恒为常数，则f(D)是区域．]5. z平面上有三个互相外切的圆周，切点之一在原点，函数w = 1/z将此三个圆周所围成的区域变成w平面上的什么区域？【解】设圆周A, B外切于原点，圆周C分别外切圆周A, B于z1, z2．由分式线性映射的保圆性，以及f(0) = ∞，知f(A), f(B)为w平面中的直线．并且因f(A), f(B)在有限z平面内无交点，f(A), f(B)为一对平行直线．因C不过原点，故f(C)为w平面中的圆周；并且，由分式线性映射的保角性，f(C)与f(A), f(B)都相切，切点分别为f(z1), f(z2)．下面的图(用sketchpad和photoshop做出，本质上是尺规作图的结果，累！)，指出圆周A, B, C的象f(A), f(B), f(C)，以及圆周A, B, C所围的区域D的象f(D)．[上面的图，我是把z平面和w平面作为一个平面来画的．因为用的是sketchpad，所以图形应该还是比较精确的．同学们可以思考：f(z) = 1/z将那三个圆所围的那个无界的(但在 ∞中是单连通的)区域变成哪个区域？]6. 如w = (az + b)/(cz + d)将单位圆周变成直线，其系数应满足什么条件？【解】首先应满足ad–bc≠ 0，以保证映射不是常值映射．其次，单位圆周上存在点α使得w(α) = ∞，这意味着cα + d = 0，因此| d | = | –cα| = | c | · | α| = | c |．反过来，若ad–bc≠ 0，| d | = | c |，则w = (az + b)/(cz + d)是分式线性映射，具有保圆性．因| –d/c | = 1，故–d/c在单位圆周上，而且w(–d/c) = ∞，故单位圆周在此映射的下的象为直线．9. 求出将圆| z – 4 i | < 2变成半平面v > u的共形映射，使得圆心变到– 4，而圆周上的点2 i变到w = 0．【解】注意到4 i和∞关于圆周| z – 4 i | = 2对称，– 4和– 4 i关于直线v = u对称；因此若分式线性映射f(z)满足f(4 i) = – 4，f(∞) = – 4 i，则f(z)将圆周| z – 4 i | = 2变成直线v = u．根据题目要求，又应有f(2 i) = 0；故可用分式线性映射的保角比性来确定共形映射w = f(z)．(w- (– 4))/(w- 0) : (– 4 i- (– 4))/(– 4 i- 0) = (z- 4 i)/(z- 2 i) : (∞- 4 i)/(∞- 2 i)；即(w- (– 4))/(w- 0) : (1 –i)/(–i) = (z- 4 i)/(z- 2 i)；所以，w = – 4i ( z– 2i)/(z- (4i + 2))．[或者，直接设f(z) = (– 4i) (z– 2i)/(z–d)，将f(4 i) = – 4代入，则– 4 = (– 4i) (4 i– 2i)/(4 i–d)，即d = 4 i +2．所以w = – 4i ( z– 2i)/(z- (4i + 2))．] 15. 求出将上半单位圆变成上半平面的共形映射，使z = 1, -1, 0分别变成w = -1, 1, ∞．【解】因f1(z) = - (z + 1)/(z- 1)把正向实轴变成正向实轴，上半平面映成上半平面，且f1(- 1) = 0，f1(0) = 1，f1(1) = ∞，故f1将实轴上的区间(0, 1)变成正实轴．由保角性，f1将上半单位圆周变成正虚轴．所以，f1将上半单位圆共形地变成第一象限．而f2(z) = z2将第一象限共形地变成上半平面．所以，f2 ◦f1将上半单位圆共形映射成上半平面，且(f2 ◦f1)(1) = ∞，(f2 ◦f1)(- 1) = 0，(f2 ◦f1)(0) = 1．注意到f1(∞) = - 1，f1(0) = 1，f1(1) = ∞；故(f1 ◦f2 ◦f1)(1) = - 1，(f1 ◦f2 ◦f1)(- 1) = 1，(f1 ◦f2 ◦f1)(0) = ∞．所以，f = f1 ◦f2 ◦f1即满足题目要求．f(z) = (f1 ◦f2 ◦f1)(z) = - ( (f2 ◦f1)(z) + 1)/( (f2 ◦f1)(z) - 1)= - ( ( f1(z)2 + 1)/( ( f1(z)2- 1)= - ( ( (- (z + 1)/(z- 1))2 + 1)/( ((- (z + 1)/(z- 1))2- 1)= - ((z + 1)2 + (z- 1)2)/( (z + 1)2 - (z- 1)2)= - 2(z2 + 1)/(4z) = (- 1/2)(z + 1/z)．17. 将扩充z平面割去1 + i到2 + 2 i的线段后剩下的区域共形映射成上半平面．【解】设割去的线段的端点分别为α, β，先做分式线性映射使得此线段变成一条以0为端点的射线(在 ∞中看成是一条以0, ∞为端点的线段)．例如可取ξ= k (z-α)/(z-β)．下面选取使当的k，使得映射将给定的线段映射成(带端点的)正实轴．为此，我们要求ξ((α + β)/2) > 0．即k (α + β)/2 -α)/(α + β)/2 -β) > 0，因此k < 0．所以，当k < 0时，ξ(z)将给定的区域映射成割去正实轴的复平面(不是扩充的)．因此，w = (k (z-α)/(z-β))1/2即为满足要求的共形映射．19. 将一个从中心起沿正实轴上的半径割开了的单位圆共形映射成单位圆，使符合条件：割缝上岸的1变成1，割缝上岸的1变成-1，0变成-i．【解】设给定的区域为D．则ξ= z1/2将D共形映射成上半单位圆 +．按第15题的论证，η = (ξ + 1)2/(ξ- 1)2将 +共形映射成上半平面 +．那么，ϕ(z) = (z1/2 + 1)2/(z1/2- 1)2将D共形映射成 +．并且，割缝上岸的1变成∞，割缝上岸的1变成0，0变成1．下面作一个分式线性映射ψ将 +共形映射成单位圆 ，并且使得ψ(∞) = 1，ψ(0) = -1，ψ(1) = -i．为满足ψ(∞) = 1，ψ(0) = -1，只要取ψ(z) = (z-α)/(z + α)；将ψ(1) = -i代入，得-i = (1 -α)/(1 + α)，即α = (1 + i)/(1 -i) = i．故ψ(z) = (z-i)/(z + i)；令f = ψ◦ϕ，则f即为满足要求的共形映射．f(z) = (ϕ(z) -i)/(ϕ(z) + i) = ((z1/2 + 1)2/(z1/2- 1)2-i)/((z1/2 + 1)2/(z1/2- 1)2 + i)= ((z1/2 + 1)2-i(z1/2- 1)2)/((z1/2 + 1)2 + i (z1/2- 1)2)= ((z + 2z1/2 + 1) -i(z - 2z1/2 + 1))/((z + 2z1/2 + 1) + i (z - 2z1/2 + 1))= ((1 -i)(z + 1) + 2(1 + i)z1/2)/((1 + i)(z + 1)+ 2(1 -i) z1/2 )= (-i) · ((z + 1) + 2i z1/2)/( (z + 1)- 2i z1/2 )．[在第17题和第19题中，我们使用了多值函数z1/2而未指明是它的哪个单值解析分支．实际上，我们是遵从了一个一般的约定：倘若未指出具体的分支，则z1/n 表示的是它的主值分支．]1. 至此，只有第六章和第七章的第二组习题尚未做完，同学们不要着急，容我慢慢做之．2. 如果还有题目，是我没有做但是同学们希望我做的，可以发Email给我，写清楚页码和题号，我将尽量满足同学们的要求．如果题目不是来自我们的教材的，一方面要打清楚，另一方面请给出题目来源：若来自书，则指明书名和作者，出版社，版次，年份；若来自互联网，则给出url；若是考研题，则指明学校，年份，最好附整个试题．3. 答疑时间定在考试前一天，上午10点开始．∀∃∅-⨯±≠≥·◦≤≡⊕⊗≅αβχδεφγηιϕκλμνοπθρστυϖωξψζ∞•︒ℵℜ℘∇∏∑⎰⊥∠ √§ψ∈∉⊆⊂⊃⊇⊄⊄∠⇒♣♦♥♠§ #↔→←↑↓⌝∨∧⋃⋂⇔⇒⇐∆∑ΓΦΛΩ∂∀m∈ +，★z∈ ∞α1, α2, ...αn lim n→∞，+n→∞∀ε > 0，∑u n，∑n≥ 1u n，m∈ ，∀ε > 0，∃δ> 0，【解】z⎰[0, 2π]l 2 dx，f(x) = (-∞, +∞)[-π, π]∑1 ≤k≤n u n，[0, 2π]。

《锐角三角函数》综合能力检测题一．选择题1．在Rt△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、∠C的对边，下列等式中，正确的是（）A．B．C．D．2．若∠A为锐角，且2cos A＜，则∠A（）A．小于30°B．大于30°C．大于45°且小于60°D．大于60°3．在Rt△ABC中，∠C＝90°，已知tan A＝，那么cos A的值是（）A．B．C．D．4．在Rt△ABC中，∠C＝90°，若m＝sin A+sin B，则（）A．0＜m＜1B．0＜m≤1C．m≥1D．1＜m＜25. 已知为锐角，，则＝（）A. B. C. D.6. 在中，，下列式子中不一定成立的是( )A. B.C. D.7. 已知：在中，，，则的值为（）A. B. C. D.8. 如图是一台54英寸的大背投彩电放置在墙角的俯视图．设∠DAO=α，彩电后背AD平行于前沿BC，且与BC的距离为60cm，若AO=100cm，则墙角O到前沿BC的距离OE是（）A．（60+100sinα）cm B．（60+100cosα）cmC．（60+100tanα）cm D．以上答案都不对9. 如图，在△ABC 中，AB=AC ，BC=12，E 为AC 边的中点，线段BE 的垂直平分线交边BC 于点D ．设BD = x ，tan ∠ACB = y ，则（ ）A. 32=-y xB. 922=-y xC. 1532=-y xD. 2142=-y x10. 如图，△ABC 中，AB=AC=10，tan A=2，BE ⊥AC 于点E ，D 是线段BE 上的一个动点，则CD +55BD 的最小值是（ ） A. 52 B. 54 C. 35 D. 1二．填空题 11．如图，△ABC 的顶点是正方形网格的格点，则tan A 的值为 ．12. 在中， ，若，则________.13. 如果为锐角，且，那么的范围是________.14. 如图，斜靠在墙上的梯子的底端到墙脚距离米，，则梯子长为________米．15．如图，若点A 的坐标为（1，），则∠1＝ ，sin ∠1＝ ．16. 如图，在Rt △ABC 中，∠ACB=90°，BC=3，AC=15，AB 的垂直平分线ED 交BC 的延长线于D 点，垂足为E ，则sin ∠CAD =________17. 设∠A 为锐角，且sin A = 93-k ，则k 的取值范围是________18. 如图，在边长相同的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，AB ，CD 相交于点P ，则=PBAP ________，tan ∠APD 的值等于_________20．如图，在热气球C 上测得两建筑物A 、B 底部的俯角分别为30°和60°．如果这时气球的垂直高度CD 为90米．且点A 、D 、B 在同一直线上，则建筑物A 、B 间的距离为 ．米．21．如图，一艘轮船在小岛A 的北偏东60°方向且距小岛80海里的B 处，沿正西方向航行一定时间后到达小岛的北偏西45°的C 处，则该船航行的路程为 海里．三．解答题22．如图，河流的两岸MN、PQ互相平行，河岸PQ上有一排间隔为50m的电线杆C、D、E…．某人在河岸MN的A 处测得∠DAN＝38°，然后沿河岸走了120m到达B处，测得∠CBN＝70°．求河流的宽度CF．（结果精确到0.1m，参考数据：sin38°≈0.62，cos38°≈0.79，tan38°≈0.78，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）23．如图，在直角坐标系中，P是第一象限的点，其坐标是（3，y），且OP与x轴的正半轴的夹角α的正切值是．求：（1）y的值；（2）角α的正弦值．24．计算：（1）﹣tan45°（2）sin30°﹣cos245°+cot260°+sin260°25．如图，在Rt△ABC中，∠B＝90°，AB＝10，sin A＝，求BC的长．26．小明家的脚踏式垃圾桶如图，当脚踩踏板时垃圾桶盖打开最大张角∠ABC＝45°，为节省家里空间小明想把垃圾桶放到桌下，经测量桌子下沿离地面高55cm，垃圾桶高BD＝33.1cm，桶盖直径BC＝28.2cm，问垃圾桶放到桌下踩踏板时，桶盖完全打开有没有碰到桌子下沿？（≈1.41 ）参考答案1. C2. B3.D4.D5.D6. D7.B8. A9. B 10. B11．． 12..13..14. 15．60°、． 16. 41 17. 3103<<k 18. 3 219．30°．20．120．21．（40+40）海里． 22．解：过点C 作CG ∥DA 交AB 于点G ．∵MN ∥PQ ，CG ∥DA ，∴四边形AGCD 是平行四边形．∴AG ＝CD ＝50m ，∠CGB ＝38°．∴GB ＝AB ﹣AG ＝120﹣50＝70（m ）．∴tan38°＝＝0.78，在Rt △BFC 中，tan70°＝＝2.75， ∴BF ＝， ∴＝＝0.78，解得：CF ≈76.2（m ）．答：河流的宽是76.2米．23．解：作PC⊥x轴于C．∵tanα＝，OC＝3，∴PC＝4，即y＝4．则OP＝5．则sinα＝．24．解：（1）原式＝﹣1＝﹣1，（2）原式＝++＝．25．解：如图，∵在Rt△ABC中，∠B＝90°，AB＝10，sin A＝，∴＝，则AC＝BC．又由勾股定理得到：AB2+BC2＝AC2，即102+BC2＝BC2，∴BC＝7.5．26解：过点C作CG⊥DE交AB于H．由题意得：四边形ABDE是矩形，∴AB∥DE，∴∠CHB＝90°，CH＝BD＝33.1，在Rt△CBH中，sin∠CBH＝，∴CH＝BC•sin∠CBH＝28.2×≈20，∴CG＝CH+HG＝33.1+20＝53.1＜55，答：桶盖完全打开时没有碰到碰到子下沿．。

第七章函数一、选择题1.以下函数声明正确的是： C 。

(02~03第一学期试题)A) double fun(int x, int y) B) double fun(int x; int y)C) double fun(int x, int y) ; D) double fun(int x , y)2.C语言规定，简单变量作实参，它与对应形参之间的数据传递方式是： B 。

（0级）A）地址传递；B）单向值传递；C）双向值传递；D）由用户指定传递方式3.以下关于Ｃ语言程序中函数的说法正确的是： B 。

（0级）Ａ）函数的定义可以嵌套，但函数的调用不可以嵌套；Ｂ）函数的定义不可以嵌套，但函数的调用可以嵌套；Ｃ）函数的定义和调用均不可以嵌套；Ｄ）函数的定义和点用都可以嵌套。

4.以下正确的函数形式是： D 。

（1级）A）double fun(int x,int y) B)fun (int x,y){z=x+y;return z;} {int z;return z;}C)fun(x,y) D)double fun(int x,int y){int x,y ; double z; {double z;z=x+y; return z;} z=x+y; return z;}5.以下说法不正确的是： B 。

（1级）C 语言规定A）实参可以是常量、变量或表达式B）形参可以是常量、变量或表达式C）实参可以是任意类型D）形参应与其对应的实参类型一致6.C语言允许函数值类型缺省定义，此时该函数值隐含的类型是 B 。

（0级）A) float型B) int 型C）long 型D）double 型7.以下错误的描述是 D 。

（0级）函数调用可以A)出现在执行语句中B)出现在一个表达式中C)做为一个函数的实参D）做为一个函数的形参8.若用数组名作为函数调用的实参，传递给形参的是 A 。

（0级）A）数组的首地址B）数组第一个元素的值C）数组中全部元素的值D）数组元素的个数9.以下正确的说法是 A 。

习题7-1下面的微分方程代表了线性定常系统，请写出它们对应的状态空间表达（a ）)(5)()(4)(22t r t c dtt dc dt t c d =++（b ）)()()()(4)(5)(02233t r d c t c dtt dc dt t c d dt t c d t =++++⎰ττ （c ）dtt dr t r t c dt t c d dt t c d )(4)()()(2)(2233+=++ 7-2 已知线性定常系统的状态方程为：Ax x =.，其中（1）⎥⎦⎤⎢⎣⎡-=2010A (2) ⎥⎦⎤⎢⎣⎡-=0110A (3)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010100010A 试求系统统的状态转移矩阵At e答案：（1）⎥⎦⎤⎢⎣⎡-=--tt Ate e e2205.05.01 （2）⎥⎦⎤⎢⎣⎡-=t t t t e Atcos sin sin cos （3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--+-+-=------)(5.0)(5.00)(5.0)(5.001)(5.0)(5.01t t t t t t t t t t t t Ate e e e e e e e e e e e e 7-3 已知系统的状态方程为：u x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=103210.，初始条件为⎥⎦⎤⎢⎣⎡=10)0(x ，试求单位阶跃收入时系统的时间响应x(t)答案：（1）求状态转移矩阵 先求出预解矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++-+++-+-+++-++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++++-+++++=⎥⎦⎤⎢⎣⎡+-=---)2(2)1(1)2(2)1(2)2(1)1(1)2(1)1(2)2)(1()2)(1(2)2)(1(1)2)(1()3(321)(11s s s s s s s s s s s s s s s s s s s s A sI对上式进行拉式反变换，即可定出：⎥⎦⎤⎢⎣⎡+-+---=--------t t t t t t t t At2222e 2e e 2e 2e e e e 2e（2）求系统的时间响应()0022()2()()2()22()2()()2()022()e e ()d 002e e e e 2e e e e d 112e 2e e 2e 2e 2e e 2e 0.50.5tAt A t t t t t t t t t t t t t t t t t t t tx t x Bu e e ττττττττττττ---------------------------=+⎡⎤⎡⎤----⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎢⎥-+-+-+-+⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤-=⎢⎥⎣⎦⎰⎰7-4 已知矩阵：（1）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=t t t t t sin cos 0cos sin 0001)(ϕ （2）⎥⎦⎤⎢⎣⎡--+=-t t t t t t t e e e e e e e t 222222)(ϕ 试问：它们可能是某个系统的状态转移矩阵吗？为什么？答案：I =)0(ϕ时才是状态转移矩阵，所以上述两个矩阵均不是某个系统的状态转移矩阵。

（完整版）答案第七章函数..第七章函数一、选择题1.以下函数声明正确的是： C 。

(02~03第一学期试题)A) double fun(int x, int y) B) double fun(int x; int y)C) double fun(int x, int y) ; D) double fun(int x , y)2.C语言规定，简单变量作实参，它与对应形参之间的数据传递方式是： B 。

（0级）A）地址传递；B）单向值传递；C）双向值传递；D）由用户指定传递方式3.以下关于Ｃ语言程序中函数的说法正确的是： B 。

（0级）Ａ）函数的定义可以嵌套，但函数的调用不可以嵌套；Ｂ）函数的定义不可以嵌套，但函数的调用可以嵌套；Ｃ）函数的定义和调用均不可以嵌套；Ｄ）函数的定义和点用都可以嵌套。

4.以下正确的函数形式是： D 。

（1级）A）double fun(int x,int y) B)fun (int x,y){z=x+y;return z;} {int z;return z;}C)fun(x,y) D)double fun(int x,int y){int x,y ; double z; {double z;z=x+y; return z;} z=x+y; return z;}5.以下说法不正确的是： B 。

（1级）C 语言规定A）实参可以是常量、变量或表达式B）形参可以是常量、变量或表达式C）实参可以是任意类型D）形参应与其对应的实参类型一致6.C语言允许函数值类型缺省定义，此时该函数值隐含的类型是 B 。

（0级）A) float型B) int 型C）long 型D）double 型7.以下错误的描述是 D 。

（0级）函数调用可以A)出现在执行语句中B)出现在一个表达式中C)做为一个函数的实参D）做为一个函数的形参8.若用数组名作为函数调用的实参，传递给形参的是 A 。

（0级）A）数组的首地址B）数组第一个元素的值C）数组中全部元素的值D）数组元素的个数9.以下正确的说法是 A 。

第七章思考与练习参考答案1 •答：函数关系是两变量之间的确定性关系，即当一个变量取一定数值时，另一个变量有确定值与之相对应；而相关关系表示的是两变量之间的一种不确定性关系，具体表示为当一个变量取一定数值时，与之相对应的另一变量的数值虽然不确定，但它仍按某种规律在定的范围内变化。

2•答：相关和回归都是研究现象及变量之间相互关系的方法。

相关分析研究变量之间相关的方向和相关的程度，但不能确定变量间相互关系的具体形式，也无法从一个变量的变化来推测另一个变量的变化情况；回归分析则可以找到研究变量之间相互关系的具体形式，并可变量之间的数量联系进行测定，确定一个回归方程，并根据这个回归方程从已知量推测未知量。

3•答：单相关系数是度量两个变量之间线性相关程度的指标，其计算公式为：总体相关系数二样本相关系数，「一】。

复相关系数是多元线性回归分析中度量因变量与其它多个自变量之间的线性相关程度的指标，它是方程的判定系数R2的正的平方根。

偏相关系数是多元线性回归分析中度量在其它变量不变的情况下两个变量之间真实相关程度的指标，它反映了在消除其他变量影响的条件下两个变量之间的线性相关程度。

4.答：回归模型假定总体上因变量Y与自变量X之间存在着近似的线性函数关系，可表示为Y^ 11X t u t，这就是总体回归函数，其中u t是随机误差项，可以反映未考虑的其他各种因素对Y的影响。

根据样本数据拟合的方程，就是样本回归函数，以一元线性回归模型的样本回归函数为例可表示为：Y?=耳+弭x t。

总体回归函数事实上是未知的，需要利用样本的信息对其进行估计，样本回归函数是对总体回归函数的近似反映。

两者的区别主要包括：第一，总体回归直线是未知的，它只有一条；而样本回归直线则是根据样本数据拟合的，每抽取一组样本，便可以拟合一条样本回归直线。

第二，总体回归函数中的-0和-1是未知的参数，表现为常数；而样本回归直线中的'?Q和?i是随机变量，其具体数值随所抽取的样本观测值不同而变动。

第7章习题答案1．f（x）=2|x|+1是从整数集合到正整数集合的函数，它的值域是什么？解：它的值域是正奇数集合。

2．试问下列关系中哪个能构成函数？（1）{〈x，y〉|x，y∈N，x+y<10}（2）{〈x，y〉|x，y∈R，y=x2}（3）{〈x，y〉|x，y∈R，y2=x}解；（1）、（3）不满足函数的定义，只有（2）是函数。

3．下列集合能够定义函数吗？如果能，求出它们的定义域和值域。

（1）{〈1,〈2,3〉〉,〈2,〈3,4〉〉,〈3,〈1,4〉〉,〈4,〈1,4〉〉}（2）{〈1,〈2,3〉〉,〈2,〈3,4〉〉,〈3,〈3,2〉〉}（3）{〈1,〈2,3〉〉,〈2,〈3,4〉〉,〈1,〈2,4〉〉}（4）{〈1,〈2,3〉〉,〈2,〈2,3〉〉,〈3,〈2,3〉〉}解：(1)、(2)、(4)定义的是函数。

(1)的定义域是{1,2,3,4},值域是{〈2,3〉,〈3,4〉,〈1,4〉}(2)的定义域是{1,2,3},值域是{〈2,3〉,〈3,4〉,〈3,2〉}(4)的定义域是{1,2,3},值域是{〈2,3〉}4．设f，g都是函数，并且有f⊆g和dom（g）=dom（f），证明f=g证明：假设f≠g，因为f⊆g和dom（g）=dom（f），则存在x1∈dom（g）和dom（f），使得〈x1,y1〉∈g但〈x1,y1〉∉f，因为f是函数，在定义域上处处有定义，所以必存在y2，使得〈x1,y2〉∈f，由f⊆g得〈x1,y2〉∈g，这与g是函数满足单值性矛盾。

故假设错误，必有f=g。

6．设X={0，1，2}，求出X X中的如下函数（1） f2（x）=f（x）（2） f2（x）=x（3） f3（x）=x解：（1）有10个函数，分别是：f1（x）={〈0,0〉,〈1,0〉,〈2,0〉}f2（x）={〈0,1〉,〈1,1〉,〈2,1〉}f3（x）={〈0,2〉,〈1,2〉,〈2,2〉}f4（x）={〈0,1〉,〈1,1〉,〈2,2〉}f5（x）={〈0,2〉,〈1,1〉,〈2,2〉}f6（x）={〈0,0〉,〈1,0〉,〈2,2〉}f7（x）={〈0,0〉,〈1,2〉,〈2,2〉}f8（x）={〈0,0〉,〈1,1〉,〈2,0〉}f9（x）={〈0,0〉,〈1,1〉,〈2,1〉}f10（x）={〈0,0〉,〈1,1〉,〈2,2〉}（2）有4个函数，分别是：f1（x）={〈0,0〉,〈1,1〉,〈2,2〉}f2（x）={〈0,0〉,〈1,2〉,〈2,1〉}f3（x）={〈0,2〉,〈1,1〉,〈2,0〉}f4（x）={〈0,1〉,〈1,0〉,〈2,2〉}（3）有3个函数，分别是：f 1（x ）={〈0,0〉,〈1,1〉,〈2,2〉}f 2（x ）={〈0,1〉,〈1,2〉,〈2,0〉}f 3（x ）={〈0,2〉,〈1,0〉,〈2,1〉}8．设f,g,h 是N → N 的函数, 其中N 是自然数集合，f(n)＝n ＋1, g(n)＝2n,⎩⎨⎧=是奇数若是偶数若n n n h 10)(试确定：f f ，f g ，g h ，h g 及(f g) h 。