第十八届北京高中数学知识应用竞赛决赛试题解答_

北京第十八中学2018年高一数学文联考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 函数f（x）=Asin（ωx+φ）的部分图象如图所示，则函数的解析式可以是（）A．f（x）=2cos（3x+）B．f（x）=2sin（）C．f（x）=2sin（3x﹣）D．f（x）=2sin（3x﹣）或f（x）=2sin（）参考答案：D【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由图形可以求出A，根据图象过（0，﹣1），（，0），把点的坐标代入求出ω，φ，从而可得函数解析式．【解答】解：由图象知A=2，点（0，﹣1），（，0）在函数图象上，∵2sinφ=﹣1，∴可得sinφ=﹣，可得：φ=2kπ+，或φ=2kπ+，k∈Z∵2sin（ω+2kπ+）=0，或2sin（ω+2kπ+）=0，∴ω+=kπ，k∈Z，或ω+=kπ，k∈Z，解得：ω=﹣3，或ω=﹣，k∈Z，∴当k=2，ω=，φ=4π+，可得函数的解析式可以是f（x）=2sin（x+4π+）=2sin（）．当k=3，ω=3，φ=6π+，可得函数的解析式可以是f（x）=2sin（3x﹣）．故选：D．【点评】本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查分析问题解决问题的能力，解题的关键是初相的求法要注意，属于中档题．2. 如图所示的纸篓，观察其几何结构，可以看出是由许多条直线围成的旋转体，该几何体的正视图为参考答案：C3. 下列四组函数中，表示同一个函数的是（）A. B.C. D.参考答案：D4. 已知圆：+=1，圆与圆关于直线对称，则圆的方程为（）A. +=1B. +=1C.+=1D.+=1参考答案：A设圆的圆心（-1,1）关于直线的对称点为，则，解得，所以圆的方程为+=1。

5. 若函数在上有零点，则的取值范围为（）A. B. C. D.参考答案：D6. 已知P为直线上的点，过点P作圆O:的切线，切点为M、N，若，则这样的点P有（）A. 0个B. 1个C. 2个 D. 无数个参考答案：B7. 设集合，，则（）A．{1} B．{0} C．{1,2} D．{0,1}参考答案：C，故选C.8. 若表示圆，则的取值范围是（）A． B．C． D．R参考答案：C9. 在正方体AC1中，AA1与B1D所成角的余弦值是（）A. B. C. D.参考答案：A10. （5分）已知向量=（cosθ，sinθ），=（1，﹣2），若∥，则代数式的值是（）A．B．C． 5 D．参考答案：C考点：三角函数的化简求值；平面向量共线（平行）的坐标表示；同角三角函数间的基本关系．专题：三角函数的求值．分析：利用共线向量的关系，求出正弦函数与余弦函数的关系，代入所求表达式求解即可．解答：向量=（cosθ，sinθ），=（1，﹣2），若∥，可得：sinθ=﹣2cosθ．==5．故选：C．点评：本题考查三角函数的化简求值，向量共线定理的应用，考查计算能力．二、填空题:本大题共7小题,每小题4分,共28分11. 将函数的图象向左平移个单位,得到的图象对应的函数为,若为奇函数,则的最小值为______参考答案：12. 求值：= ．参考答案：19【考点】对数的运算性质；有理数指数幂的化简求值．【专题】计算题．【分析】根据式子的特点需要把底数和真数表示成幂的形式，把对数前的系数放到真数的指数位置，利用恒等式，进行化简求值．【解答】解：原式=9﹣3×（﹣3）+=18+1=19，故答案为：19．【点评】本题的考点是对数和指数的运算性质的应用，常用的方法是把（底数）真数表示出幂的形式，或是把真数分成两个数的积（商）形式，根据对应的运算法则和“”进行化简求值．13. 若直线过点(1,2)，则的最小值为___________．参考答案：814. 经过点，且在轴上的截距等于在轴上的截距的倍的直线的方程是___________．参考答案：略15. 如果角α是第二象限角，则点P（tanα，secα）位于第象限．参考答案：三【考点】任意角的三角函数的定义．【分析】由于角α是第二象限角可得tanα＜0，secα＜0，从而可得答案．【解答】解：∵角α是第二象限角，∴tanα＜0，secα＜0，即点P（tanα，secα）位于第三象限．故答案为三．16. 已知函数,若时，恒成立，求的取值范围_________________________参考答案：[-7，2]17. ．如图，在正方体ABCD—A1B1C1D1中，E，F分别是正方形A1B1C1D1和ADD1A1的中心，则EF和BD所成的角是。

2016年全国高中数学联赛（B 卷）一试一、选择题：（每小题8分，共64分）1.等比数列{}n a 的各项均为正数，且213263236,a a a a a ++=则24a a +的值为 ．2.设{}|12A a a =-≤≤，则平面点集(){},|,,0B x y x y A x y =∈+≥的面积为 ．3.已知复数z 满足22z z z z +=≠（z 表示z 的共轭复数），则z 的所有可能值的积为 ．4.已知()(),f x g x 均为定义在R 上的函数，()f x 的图像关于直线1x =对称，()g x 的图像关于点()1,2-中心对称，且()()391x f x g x x +=++，则()()22f g 的值为 ．5.将红、黄、蓝3个球随机放入5个不同的盒子,,,,A B C D E 中，恰有两个球放在同一盒子的概率为 ．6.在平面直角坐标系xOy 中，圆221:0C x y a +-=关于直线l 对称的圆为222:2230,C x y x ay ++-+=则直线l 的方程为 ．7.已知正四棱锥V -ABCD 的高等于AB 长度的一半，M 是侧棱VB 的中点，N 是侧棱VD 上点，满足2DN VN =，则异面直线,AM BN 所成角的余弦值为 ．8.设正整数n 满足2016n ≤，且324612n n n n ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭．这样的n 的个数为 ．这里{}[]x x x =-，其中[]x 表示不超过x 的最大整数．二、解答题：（共3小题，共56分）9.（16分）已知{}n a 是各项均为正数的等比数列，且5051,a a 是方程()2100l g l g 100x x =的两个不同的解，求12100a a a 的值．10.（20分）在ABC 中，已知23.AB AC BA BC CA CB ⋅+⋅=⋅（1）将,,BC CA AB 的长分别记为,,a b c ，证明：22223a b c +=； （2）求cos C 的最小值．11.（20分）在平面直角坐标系xOy 中，双曲线C 的方程为221x y -=．求符合以下要求的所有大于1的实数a ：过点(),0a 任意作两条互相垂直的直线1l 与2l ，若1l 与双曲线C 交于,P Q 两点，2l 与C 交于,R S 两点，则总有PQ RS =成立．加试一、（40分）非负实数122016,,,x x x 和实数122016,,,y y y 满足： （1）221,1,2,,2016k k x y k +==； （2）122016y y y +++是奇数．求122016x x x +++的最小值．二、（40分）设,n k 是正整数，且n 是奇数．已知2n 的不超过k 的正约数的个数为奇数，证明：2n 有一个约数d ，满足2.k d k <≤三、（50分）如图所示，ABCD 是平行四边形，G 是ABD 的重心，点,P Q 在直线BD 上，使得,.GP PC GQ QC ⊥⊥证明：AG 平分.PAQ ∠QGPD CBA四、（50分）设A 是任意一个11元实数集合．令集合{}|,,.B uv u v A u v =∈≠求B 的元素个数的最小值．2016年全国高中数学联赛（B 卷）试题及答案一试一、选择题：（每小题8分，共64分）1.等比数列{}n a 的各项均为正数，且213263236,a a a a a ++=则24a a +的值为 ．答案：6．解：由于()2222132632424243622,a a a a a a a a a a a =++=++=+且240,aa +>故24 6.a a +=另解：设等比数列的公比为q ，则52611.a a a q a q +=+又因()()()()()22252132********2223331111112436222,a a a a a a a q a q a q a q a q a q a q a q a q a q aa =++=⋅+⋅+=+⋅⋅+=+=+而240a a +>，从而24 6.a a +=2.设{}|12A a a =-≤≤，则平面点集(){},|,,0B x y x y A x y =∈+≥的面积为 ． 答案：7．解：点集B 如图中阴影部分所示，其面积为133227.2MRSMNPQ S S-=⨯-⨯⨯=正方形3.已知复数z 满足22z z z z +=≠（z 表示z 的共轭复数），则z 的所有可能值的积为 ．答案：3．解：设()i ,.z a b a b R =+∈由22z z z +=知，222i 22i i,a b ab a b a b -+++=-比较虚、实部得220,230.a b a ab b -+=+=又由z z ≠知0b ≠，从而有230,a +=即32a =-，进而23b a a =±+于是，满足条件的复数z 的积为33 3.22⎛⎫⎛⎫-+-= ⎪⎪⎪⎪⎝⎭⎝⎭4.已知()(),f x g x 均为定义在R 上的函数，()f x 的图像关于直线1x =对称，()g x 的图像关于点()1,2-中心对称，且()()391x f x g x x +=++，则()()22f g 的值为 ．答案：2016. 解：由条件知()()002,f g +=①()()22818190.f g +=++=②由()(),f x g x 图像的对称性，可得()()()()02,024,f f g g =+=-结合①知，()()()()22400 2.f g f g --=+=③由②、③解得()()248,242,f g ==从而()()2248422016.f g =⨯=另解：因为()()391x f x g x x +=++，①所以()()2290.f g +=②因为()f x 的图像关于直线1x =对称，所以()()2.f x f x =-③又因为()g x 的图像关于点()1,2-中心对称，所以函数()()12h x g x =++是奇函数，()()h x h x -=-，()()1212g x g x ⎡⎤-++=-++⎣⎦，从而()()2 4.g x g x =---④将③、④代入①，再移项，得()()3229 5.x f x g x x ---=++⑤在⑤式中令0x =，得()()22 6.f g -=⑥由②、⑥解得()()248,246.f g ==于是()()222016.f g =5.将红、黄、蓝3个球随机放入5个不同的盒子,,,,A B C D E 中，恰有两个球放在同一盒子的概率为 ．解：样本空间中有35125=个元素．而满足恰有两个球放在同一盒子的元素个数为223560.C P ⨯=过所求的概率为6012.12525p == 6.在平面直角坐标系xOy 中，圆221:0C x y a +-=关于直线l 对称的圆为222:2230,C x y x ay ++-+=则直线l 的方程为 ．答案：2450.x y -+= 解：12,C C 的标准方程分别为()()2222212:1,:1 2.C x y C x y a a +=++-=-2故12,C C 12O O 7.是侧棱 xA建立空间直角坐标系．不妨设2,AB =此时高1,VO =从而()()()()1,1,0,1,1,0,1,1,0,0,0,1.A B D V ----由条件知111112,,,,,222333M N ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭，因此311442,,,,,.222333AM BN ⎛⎫⎛⎫==- ⎪ ⎪⎝⎭⎝⎭设异面直线,AM BN 所成的角为θ，则cos 11AM BN AM BNθ⋅-===⋅ 8.设正整数n 满足2016n ≤，且324612n n n n ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭．这样的n 的个数为 ．这里{}[]x x x =-，其中[]x 表示不超过x 的最大整数．解：由于对任意整数n ，有135113,2461224612n n n n ⎧⎫⎧⎫⎧⎫⎧⎫+++≤+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭ 等号成立的充分必要条件是()1mod12n ≡-，结合12016n ≤≤知，满足条件的所有正整数为()1211,2,,168,n k k =-=共有168个．另解：首先注意到，若m 为正整数，则对任意整数,x y ，若()mod x y m ≡，则.x y m m ⎧⎫⎧⎫=⎨⎬⎨⎬⎩⎭⎩⎭这是因为，当()mod x y m ≡时，x y mt =+，这里t 是一个整数，故 .x x x y mt y mt y y y y y t t m m m m m m m m m m ++⎧⎫⎡⎤⎡⎤⎡⎤⎡⎤⎧⎫=-=-=+-+=-=⎨⎬⎨⎬⎢⎥⎢⎥⎢⎥⎢⎥⎩⎭⎣⎦⎣⎦⎣⎦⎣⎦⎩⎭因此，当整数12,n n 满足()12mod12n n ≡时，11112222.2461224612n n n n n n n n ⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫⎧⎫+++=+++⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭⎩⎭容易验证，当正整数满足112n ≤≤时，只有当11n =时，等式324612n n n n ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭才成立．而201612168=⨯，故当12016n ≤≤时，满足324612n n n n ⎧⎫⎧⎫⎧⎫⎧⎫+++=⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭正整数n 的个数为168. 二、解答题：（共3小题，共56分）9.（16分）已知{}n a 是各项均为正数的等比数列，且5051,a a 是方程()2100lg lg 100x x =的两个不同的解，求12100a a a 的值．解对50,51k =，有()2100lg lg 1002lg ,k k k a a a ==+即()2100lg lg 20.k k a a --=因此，5051lg ,lg a a 是一元二次方程210020t t --=的两个不同实根，从而()505150511lg lg lg ,100a a a a =+=即1100505110.a a =由等比数列的性质知，()5015010012100505110a a a a a ⎛⎫=== ⎪⎝⎭10.（20分）在ABC 中，已知23.AB AC BA BC CA CB ⋅+⋅=⋅ （1）将,,BC CA AB 的长分别记为,,a b c ，证明：22223a b c +=； （2）求cos C 的最小值．解（1）由数量积的定义及余弦定理知，222cos .2b c a AB AC cb A +-⋅==同理得，222222,.22a cb a b cBA BC CA CB +-+-⋅=⋅=故已知条件化为()()22222222223,b c a a c b a b c +-++-=+-即22223.a b c +=（2）由余弦定理及基本不等式，得()2222222123cos 2236a b a ba b c C ab ab a b b a+-++-===+≥ 等号成立当且仅当因此cos C 11.（20分）在平面直角坐标系xOy 中，双曲线C 的方程为221x y -=．求符合以下要求的所有大于1的实数a ：过点(),0a 任意作两条互相垂直的直线1l 与2l ，若1l 与双曲线C 交于,PQ 两点，2l 与C 交于,R S 两点，则总有PQ RS =成立．解过点(),0a 作两条互相垂直的直线1:l x a =与2:0.l y =易知，1l 与C 交于点((00,,P a Q a （注意这里1a >），2l 与C 交于点()()001,0,1,0,R S -由条件知00002PQ R S ===，解得a这意味着符合条件的a 下面验证a =事实上，当12,l l中有某条直线斜率不存在时，则可设12:,:0l x a l y ==，就是前面所讨论的12,l l 的情况，这时有.PQ RS =若12,l l 的斜率都存在，不妨设((()121:,:0,l y k x l y x k k==-≠ 注意这里1k ≠±（否则1l 将与C 的渐近线平行，从而1l 与C 只有一个交点）．联立1l 与C 的方程知，(22210,x k x ---=即()22221210,k xx k ----=这是一个二次方程式，其判别式为2440k ∆=+>．故1l 与C 有两个不同的交点,P Q ．同样，2l 与C 也有两个不同的交点,.R S 由弦长公式知，2212.1k PQ k +==⋅-用1k -代替k ，同理可得()()22221122.11k k RS k k --+-+=⋅=---于是.PQ RS= 综上所述，a =加试一、（40分）非负实数122016,,,x x x 和实数122016,,,y y y 满足： （1）221,1,2,,2016k k x y k +==； （2）122016y y y +++是奇数．求122016x x x +++的最小值．解：由已知条件（1）可得：1,1,1,2,,2016,k k x y k ≤≤=于是（注意0i x ≥）()2016201620162016201622211111120162016.kkkkk k k k k k x xy yy =====≥=-=-≥-∑∑∑∑∑①不妨设112016,,0,,,0,02016,m m y y y y m +>≤≤≤则201611,2016.m kk k k m ym y m ==+≤-≤-∑∑若11m k k y m =>-∑，并且201612015,k k m y m =+->-∑令2016111,2015,m kk k k m ym a y m b ==+=-+-=-+∑∑则0,1,a b <<于是()201620161111201522016,m kkk k k k m y yy m a m b m a b ===+=+=-+--+=-+-∑∑∑由条件（2）知，20161k k y =∑是奇数，所以a b -是奇数，这与0,1a b <<矛盾．因此必有11m k k y m =≤-∑，或者201612015,k k m y m =+-≤-∑则201620161112015.m kk k k k k m yy y ===+=-≤∑∑∑于是结合①得201611.k k x =≥∑又当122015201612201520160,1,1,0x x x x y y y y ==========时满足题设条件，且使得不等式等号成立，所以122016x x x +++的最小值为1．二、（40分）设,n k 是正整数，且n 是奇数．已知2n 的不超过k 的正约数的个数为奇数，证明：2n 有一个约数d ，满足2.k d k <≤证明：记{}||2,0,A d d n d k d =<≤是奇数，{}||2,0,B d d n d k d =<≤是偶数，则,2A B n =∅的不超过k 的正约数的集合是.A B若结论不成立，我们证明.A B =对d A ∈，因为d 是奇数，故2|2d n ，又22d k ≤，而2n 没有在区间(],2k k 中的约数，故2d k ≤，即2d B ∈，故.A B ≤反过来，对d B ∈，设2d d '=，则|d n '，d '是奇数，又2kd k '≤<，故,d A '∈从而B ≤ABD 直线.PAQCB此，点G 在线段AC 上．由于90GPC GQC ∠=∠=，所以,,,P G Q C 四点共圆，并且其外接圆是以GC 为直径的圆．由相交弦定理知.PM MQ GM MC ⋅=⋅①取GC 的中点.O 注意到::2:1:3,AG GM MC =故有1,2OC GC AG ==因此,G O 关于点M 对称．于是.GM MC AM MO ⋅=⋅②结合①、②，有PM MQ AM MO ⋅=⋅，因此,,,A P O Q 四点共圆． 又1,2OP OQ GC ==所以PAO QAO ∠=∠，即AG 平分.PAQ ∠四、（50分）设A 是任意一个11元实数集合．令集合{}|,,.B uv u v A u v =∈≠求B 的元素个数的最小值．解：先证明17.B ≥考虑到将A 中的所有元素均变为原来的相反数时，集合B 不变，故不妨设A 中正数个数不少于负数个数．下面分类讨论：情况一：A 中没有负数． 设1211a a a <<<是A 中的全部元素，这里120,0,a a ≥>于是1223242113111011,a a a a a a a a a a a a <<<<<<<上式从小到大共有19818++=个数，它们均是B 的元素，这表明18.B ≥情况二：A 中至少有一个负数．设12,,,k b b b 是A 中的全部非负元素，12,,,l c c c 是A 中的全部负元素．不妨设110,l k c c b b <<<≤<<其中,k l 为正整数，11k l +=，而k l ≥，故 6.k ≥于是有111212,k k l k c b c b c b c b c b >>>>>>它们是B 中的110k l +-=个元素，且非正数；又有23242526364656,b b b b b b b b b b b b b b <<<<<<它们是B 中的7个元素，且为正数．故10717.B ≥+=由此可知，17.B ≥另一方面，令{}2340,1,2,2,2,2,A =±±±±±则{}236780,1,2,2,2,,2,2,2B =-±±±±±-是个17元集合．。

第十八届北京高中数学知识应用竞赛初赛参考解答一、（满分20分）一片枫叶紧紧地嵌在一个矩形框内部，即矩形的各边上都有枫叶边缘上的点，如右图．假设这个矩形框的每一条边都可以伸缩，令枫叶不动，矩形框转动，依靠框的伸缩始终保持这片枫叶紧紧地嵌在它的内部，而框始终是矩形．请说明，存在一个转动位置，这时的这片枫叶恰紧紧地嵌在一个正方形的内部．解：设转动前的矩形的长和宽的长度分别为a 和b ．若a −b =0，这个矩形就是正方形．若a −b ≠0，不妨设a −b ＜0．在矩形转动时，a −b 的值也会随之变化．当旋转90º后，得到的矩形和最初的矩形重合，但a −b ＞0了．即a −b 的值是在[0,90º]上的转动角θ的连续函数，设a −b =f (θ)，于是，f (0)＜0，f (90º)＞0，由函数的零点存在定理可知，在上述转动中，一定有一个位置θ0，使f (θ0)=0，即a −b =0，这时的矩形框就是正方形框．从而这片枫叶恰紧紧地嵌在一个正方形框内部．二、（满分20分）野外失火，火势以失火点为中心，匀速的向四周呈圆形蔓延．在火情发生t 0时间后，消防队员发现火情，随即迅速开始修建防火带．（1）消防队员修建的防火带是以失火点为圆心的圆，从该圆上的某一点同时向这点的两侧分别以火蔓延的速度的4倍修建防火带，求防火带围成的最小面积S ．（2）再给出一个修建防火带的方案？使防火带围成的面积比S 小．解：（1）设修建防火带的时间为t ，火势的蔓延速度为v ，修建的圆形防火带的半径R 不小于火势蔓延的圆的半径r ．因为πR =4vt ，r =v (t 0+t )，当面积取S 时，R =r ，即04()vt v t t π=+，得04t t ππ=−，所以，S =πR 2=24()vt ππ=22216(4)v t ππ−．（2）因为04t t ππ=−≈3.65t 0，不难得出，如果（1）的方案是从A 处开始修建，那么，向失火点方向靠近一点儿取点B （比如AB =1.5t 0，如右图），从这一点向垂直于AB 的两边修建，至C 、D 后，再修建圆弧形，即整个防火带围成的形状比圆少了一个弓形，面积缩小了．（缩小面积的方案很多，只要计算无误即算正确）三、（满分20分）广发银行推出一款理财产品“广发银行薪满益足140925版网银专属版”，42天，投资起点50,000元，高于投资起点金额部分应为1000元份整数倍．销售费率0.10%—0.30%，托管费率0.03%．年化收益率预计为5.35%，发售期为2014年9月24日至2014年10月7日，收益起始日期为10月8日，收益终止日期为11月19日，单利计算利息．理财产品中途若取出，则按银行活期利率计算利息．收益公式：理财收益=申购本金×理财产品实际年化收益率×365实际理财天数其中，实际年化收益率=年化收益率−销售费率−托管费率．BA CD示例：理财本金为5万元，实际理财天数为197天，理财产品到期实际年化收益率为5.70%，则投资者的理财收益=50000×5.7%×197365=1538.22元．华夏基金公司推出一款货币型基金“华夏财富宝”，该基金的收益分配是按日结转份额的，每日收益支付方式只采用红利再投资（即红利转基金份额）方式．该货币型基金除去法定休息日外，随时可以申购和赎回，没有时间的限制．一般规定在交易日的15:00前赎回，资金到帐为2个交易日（T+2日）．日每万份基金净收益和7日年化收益率的计算方法如下：日每万份基金净收益=当日基金份额的已实现收益当日基金份额总额×100007日年化收益率（%）=365717111100% 1000010000R R⎧⎫⎡⎤⎪⎪⎛⎞⎛⎞+××+−×⎨⎬⎜⎟⎜⎟⎢⎥⎝⎠⎝⎠⎣⎦⎪⎪⎩⎭⋯其中，R i为最近第i个自然日（包括计算当日）的每万份基金净收益．每万份基金净收益采用四舍五入保留至小数点后第4位，7日年化收益率采用四舍五入保留至百分号内小数点后第2位．表1为2014年10月8日至11月18日“华夏财富宝”的日每万份基金净收益和7日年化收益率．投资人手上恰有10万块钱，10月8日至11月19日期间想进行投资，请问：（1）为了获得最大收益，投资人是投资“广发银行薪满益足140925版网银专属版”还是“华夏财富宝”？两种投资的差额为多少？（2）投资人想尽可能地保持资金的流动性（保证尽可能多的资金随时可用），那么10万块对两种产品如何配置，能使得获得的收益介于两者中最高收益的95%与最小收益的110%之间？解：（1）“广发银行薪满益足140925版网银专属版”单利计算利息，投资42天，当销售费率为0.30%时，收益为42100000 5.35%0.3%0.03%577.64365×−−×=（）．“华夏财富宝”复利计算利息，投资42天，收益为12421000001111496.57100001000010000R R R ⎡⎤⎛⎞⎛⎞⎛⎞×+⋅+⋅⋅+−=⎜⎟⎜⎟⎜⎟⎢⎥⎝⎠⎝⎠⎝⎠⎣⎦⋯．因此投资“广发银行薪满益足140925版网银专属版”收益高．二者比较，差额为81.07元．（2）获得的收益介于两者中最高收益的95%和最小收益的110%之间，即为收益小于577.64×0.95=548.758元，大于496.57×1.1=546.227元．设分别投资“广发银行薪满益足140925版网银专属版”和“华夏财富宝”x 1、x 2元，列方程为1124221242546.227(5.35%0.3%0.03%)3651111548.758100001000010000100000x R R R x x x ⎧<⋅−−×⎪⎪⎪⎡⎤⎛⎞⎛⎞⎛⎞⎨+⋅+⋅+⋅⋅+−<⎜⎟⎜⎟⎜⎟⎢⎥⎪⎝⎠⎝⎠⎝⎠⎣⎦⎪+=⎪⎩⋯解得1612465.43.726740x <<，但由于高于投资起点金额部分应为1000元份整数倍，因此分别投资“广发银行薪满益足140925版网银专属版”和“华夏财富宝”62000元和38000元，或63000元和37000元．四、（满分20分）储药柜的结构类似于书橱，从上到下有若干层横向隔板，每一层称为一个储药槽．每个储药槽内用竖向隔板隔开，形成若干个存放药盒的储药格．一个储药槽内只能摆放同一种药品．右图为并排的三个储药柜．为保证药品从储药格内顺利取出，要求放入药盒后，储药格内留有不小于2mm 的横向间隙，同时还要求药盒在储药格内放置时不会出现并排重叠（一个格内不能放两个药盒）、药盒不能在格内侧翻或水平旋转．假设药盒的长度＞宽度＞厚度，并且药盒在格内放置时要求（长×宽）面在左右，（宽×厚）面在前后，（长×厚）面在上下．为方便储药柜的制造，储药格的宽度类型越少越好．不同尺寸的药盒种类有成百上千种．表2所列的仅仅是20个不同的样品．请你就这20种药盒尺寸规格，给出能够存放这些药盒，且满足上述要求的储药格宽度类型最少的设计方案（无需考虑存放药盒的数量多少）．表2（度量单位：mm ）药盒编号长度宽度厚度药盒编号长度宽度厚度112076241195553321257220121086218312576211395553349171151413476205125722115955533612085201685464671173726171257533878652018116761691175656191001001010744740201317738解：药盒的长，宽，厚分别为记为a ,b ,c ．则有a ＞b ＞c ．假设用d 表示出药槽内竖隔板之间的宽度．欲使药盒在格内放置时不会出现并排重叠，必须有c ＜d ＜2c （1）欲使药盒不能在格内侧翻，必须有d（2）欲使药盒不能在格内水平旋转，必须有d（3）由（1）、（2）、（3），隔板之间的宽度必须满足c ＜d ＜min{2c,,（4）由于a ≥b ，再由（4），得c ＜d ＜min{2c,}（*）当b时，有2c ．由（*），隔板之间的宽度应取2c ．当c ≤b≤时，有2c=．由（*），隔板之间的宽度应．综上，隔板之间的宽度应取．这表明，在满足不会出现并排重叠和侧翻、或0+2的储药格内可以存放的药盒厚度c 的范围是c 0≤c0．由表2可知，药盒的厚度分布在10mm 至56mm 之间，于是，最少需要五种间隔，见表（2）．为了寻找S 与A 的关系，先将A =4×10k 变形为4A =10k ，两边取对数，得k =lg 4A，又2=10lg2,于是S =5×2k =5(10lg2)lg 4A =5(10lg 4A )lg2=5(4A )lg2=(lg 254)A lg2=3.29A lg2=3.29A 0.301．即物种的数量是岛屿的面积的函数，其表达式是S =3.29A 0.301．表（2）度量单位：mm 储药格宽度存储药盒的厚度14.1+210.0—14.120.0+214.1—20.028.2+220.0—28.240.0+228.2—40.056.4+240.0—56.4。

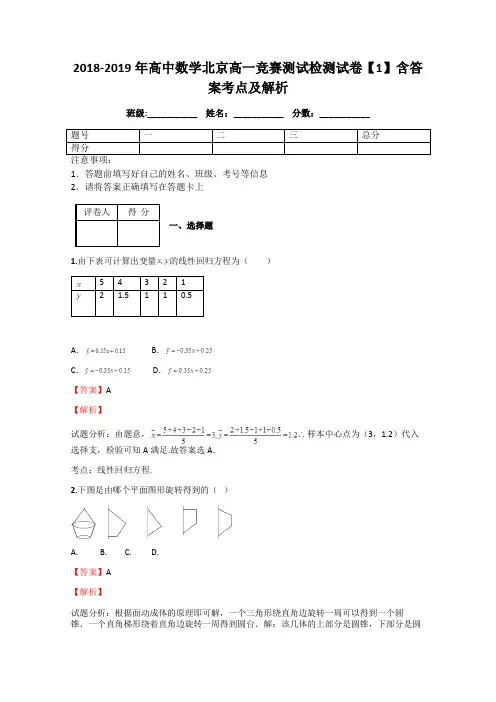
2018-2019年高中数学北京高一竞赛测试检测试卷【1】含答案考点及解析班级:___________ 姓名：___________ 分数：___________1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、选择题1.由下表可计算出变量的线性回归方程为（）543212A． B．C． D．【答案】A【解析】试题分析：由题意，∴样本中心点为（3，1.2）代入选择支，检验可知A满足.故答案选A．考点：线性回归方程.2.下图是由哪个平面图形旋转得到的（）A. B. C. D.【答案】A【解析】试题分析：根据面动成体的原理即可解，一个三角形绕直角边旋转一周可以得到一个圆锥．一个直角梯形绕着直角边旋转一周得到圆台．解：该几体的上部分是圆锥，下部分是圆台，圆锥的轴截面是直角三角形，圆台的轴截面是直角梯形，∴这个几何图形是由直角三角形和直角梯形围绕直角边所在的直线为轴旋转一周得到．故选A考点：旋转体点评：本题主要考查空间感知能力，难度不大，学生应注意培养空间想象能力．3.cos300°＝ ()A．－B．－C．D．【答案】C【解析】试题分析：利用诱导公式把要求的式子化为 cos（360°-60°）=cos60°，由此求得结果．解：cos300°=cos（360°-60°）=cos60°=，故选C考点：诱导公式和特殊角的三角函数值点评：本题主要考查应用诱导公式化简三角函数式，要特别注意符号的选取，这是解题的易错点．4.下列函数中，在区间上是增函数的是（）A．B．C．D．【答案】C【解析】试题分析：根据基本初等函数的单调性知，在上单调递减；在上单调递减；在上单调递增；在上单调递减.考点：本小题主要考查基本初等函数的单调性.点评：考查函数的单调性，要记住基本初等函数的单调性，结合图象解决问题.5.若角和角的终边关于轴对称，则（）A．，B．，C．，D．，【答案】A【解析】试题分析：因为α，β角的终边关于y轴对称，所以，即α+β=π+2kπ，（k∈z），考点：终边相同的角。

路漫漫其修远兮2018 年全国高中数学联合竞赛加试（A 卷）参考答案及评分标准说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10 分为一个档次，不得增加其他中间档次．一、（本题满分40 分）设n是正整数，1, 2, , n, 1, 2, , n, ,a a ab b b A B均为正b b b B实数，满足, , 1, 2, , ≤a≤b a≤A i=n，且1 2 n．a a a Ai i i1 2 n(b+1)(b+1) (b+1) ≤B+1证明： 1 2 ．n(a+1)(a+1) (a+1) A+11 2 nb B b b b B证明：由条件知，i1, 1, 2, , ≤化为k i n=K，则 1 2 n=≥=．记ia A a a a Ai 1 2 nk k k≤K．要证明1 2 nn k a+≤KA+1 1∏．①i ia+1A+1 i=1 i对i=1, 2,, n，由于 1k≥及0 <a≤A知，i ik a+1 =−k−1 ≤−k−1 =k A+1i i k i k i i．a 1a 1A 1A 1 + i+ i++ii结合K ≥ k kk 知，为证明①，仅需证明当 A > 0, k ≥ 1(i = 1, 2,, n ) 时，有1 2ni∏nk Ak k k A+1 ≤+1 in．②1 2A +1 A +1 i =1…………………20 分对n 进行归纳．当n =1时，结论显然成立． 当n = 2时，由 A > 0, k , k ≥1 可知12k A 1 k A 1 k k A 1A (k 1)(k 1) + ⋅+ −+ = − −− ≤121 212 A +1 A +1 A +1 (A +1)2， ③ 因此n = 2时结论成立． …………………30 分设n = m 时结论成立，则当n = m +1时，利用归纳假设知，∏∏mk A +1m k A+1⋅ k A +1 ≤ k kk A +1⋅ k A +1+1ii m +11 2mm +1A+1A+1A +1 A +1A +1 i =1i =1k kk + A + 1 211≤m，A +1最后一步是在③中用 12m , m 1 1 2m 1,m 111, 2k k k k + （注意 k k k ≥ k + ≥ ）分别代替从而n = m +1时结论成立．k k ．由数学归纳法可知，②对所有正整数n 成立，故命题得证．…………………40 分1吾将上下而求索路漫漫其修远兮二、（本题满分40分）如图，ABC为锐角三角形，AB AC，M为BC边的中点，点D和E分别为ABC的外接圆B AC和B C的中点，F为ABC的内切圆在AB边上的切点，G为AE与BC的交点，N在线段EF上，满足NB AB．证明：若BN EM，则DF FG．（答题时请将图画在答卷纸上）DAFB CGMNE证明：由条件知，DE为ABC外接圆的直径，DE BC于M，AE AD．记I为ABC的内心，则I在AE上，IF AB．由NB AB可知NBE ABE ABN(180 ADE) 90．①…………………10 分90 ADE MEI又根据内心的性质，有EAB ABI EIB，EBI EBC CBI EAC ABI从而BE EI．结合BN EM及①知，NBE≌MEI．…………………20 分DAFIB CGMNE于是EMI BNE90BFE180EFI，故E, F, I, M四点共圆．进而可知AFM90IFM90IEM AGM，从而A, F, G, M四点共圆．…………………30 分再由DAG DMG90知，A, G, M, D四点共圆，所以A, F, G, M, D五点共圆．从而DFG DAG90，即DF FG．…………………40 分2吾将上下而求索路漫漫其修远兮2k −1三、（本题满分 50 分）设n , k , m 是正整数，满足 k ≥ 2 ，且 ≤ < ．n m nkn设 A 是{1,2,,m }的 n 元子集．证明：区间 0,中的每个整数均可表示为−k1a − a ′ ，其中a , a ′∈ A ．n证明：用反证法．假设存在整数0, −x不可表示为 a − a ′ ，a , a ′∈ A ．作k 1带余除法m = xq + r ，其中0 ≤ r < x ．将1, 2,, m 按模 x 的同余类划分成 x 个公差为 x 的等差数列，其中 r 个等差数列有 q +1项， x − r 个等差数列有 q 项．由于 A 中没有两数之差为 x ，故 A 不能包含以 x 为公差的等差数列的相邻两项．从而⋅ q 1 + x , 2 q,+1()2qqn = A ≤ r+ x − r=①22⋅ q +x r , 2 | q ,2这里α表示不小于α 的最小整数．…………………20 分由条件，我们有k kn > m = (xq + r ) 2k −1 2k −1．②n 又 x0, −k 1 ，故n > (k −1)x ．③情形一： q 是奇数．则由①知，q +1 n ≤ x ⋅．④2q+1 k k结合②，④可知，x⋅≥n>(xq+r) ≥xq，从而q<2k−1．再由q2 2k−1 2k−1是奇数可知，q≤2k−3，于是q+1n≤x⋅≤(k−1)x，2与③矛盾．情形二：q是偶数．则由①知，qn≤x⋅+r．⑤2q k xq k−1 (k−1)x结合②，⑤可知，x⋅+r≥n>(xq+r) <r<，从而，2 2k−1 2(2k−1) 2k−1 2k−1故q<2(k−1) ．再由q是偶数可知，q≤2k−4 ，于是qn≤x⋅+r≤(k−2)x+r<(k−1)x，2与③矛盾．综上可知，反证法假设不成立，结论获证．…………………50 分3吾将上下而求索路漫漫其修远兮四、（本题满分50分）数列{a}定义如下：a是任意正整数，对整数n≥1，n 1n∑互素，且不等于a+是与an 1 ii=1 a a的最小正整数．证明：每个正整数均在数1, , n a a的最小正整数．证明：每个正整数均在数列{a}中出现．n证明：显然 1 1 2 1a=或a=．下面考虑整数m>1，设m有k个不同素因子，我们对k归纳证明m在{a}中出现．记S=a ++a，n≥1．n n 1 nk=时，m是素数方幂，设m=pα，其中α>0 ，p是素数．假设m不在{ }1 an中出现．由于{a}各项互不相同，因此存在正整数N，当n≥N时，都有a>pα．若n n对某个n≥N，p S，那么pα与a a中无一项是pS互素，又1, , nα，故由数列n n定义知a+≤pα，但是a+>pα，矛盾！n1 n 1因此对每个n≥N，都有p| S．但由p| S+及p| S n知p| a n+1，从而a n+1 与S nn n1不互素，这与a+的定义矛盾．…………………10 分n 1假设k≥2 ，且结论对k−1成立．设m的标准分解为=．假设mm p p pααα1 2 k1 2 k不在{a}中出现，于是存在正整数N′，当n≥N′时，都有a>m．取充分大的正n n整数−，使得ββ1,, k1M=pβpβ>a．max1 k−11 k−1 ≤≤′n1 n N我们证明，对n≥N′，有a+≠M．…………………20 分n 1对任意n≥N′，若p p p互素，则m与a a中均S与S互素，又m在1, , nn 1 2 k n未出现，而a+>m，这与数列的定义矛盾．因此我们推出：n 1对任意n≥N′，p p p不互素．(∗)S与n 1 2 k情形1．若存在i(1≤i≤k−1) ，使得p| S，因+，从而(a+, S) =1，故p ai n n1 n i n1a+≠M（因|p M）．…………………30 分n 1 i情形2．若对每个i(1≤i≤k−1) ，均有p S．于是p S，则由(∗) 知必有|i n k np a+，进而p S a p S+，即+．故由(∗) 知，存在0 (1 0 1)i≤i≤k−，使得k n 1 k n n+1 k n 1p0 | S+1，再由S n+1 =S n+a n+1 及前面的假设p S(1≤i≤k−1)，可知p ai n i n0 1i n+，故a+≠M． (40)分n 1因此对n≥N′+1，均有a≠M，而>，故M不在{ }M max a a中出现，这与n n n1≤i≤N′归纳假设矛盾．因此，若m有k个不同素因子，则m一定在{a}中出现．n由数学归纳法知，所有正整数均在{a}中出现．…………………50 分n4吾将上下而求索。

第十八届北京市大学生数学竞赛本科甲、乙组试题解答（2007年10月14日 下午2：30--5：00）注意：本考卷共九题. 甲组九题全做, 乙组只做前七题一、填空题（每小题2分，共20分） 1. 设当1→x 时，111-+++-m x x m是1-x 的等价无穷小，则=m ．解 3=m ． 2. 设)()2)(1()()2)(1()(n x x x n x x x x f +++---=，则=')1(f ．解 )1()1()1(1+-='-n n f n ．3. 已知曲线)(x f y =在点)0,1(处的切线在y 轴上的截距为1-，则=++∞→n n nf )]11(1[lim ． 解 e n f nn =++∞→)]11(1lim[．4. =+∑=∞→nk nk n kn e11lim．解 原式1-=e ．5.=++⎰-x x xx d )cos 1(sin 2222ππ．解 原式4-=π．6. 设函数),(y x f z =在点)1,0(的某邻域内可微，且)(321)1,(ρo y x y x f +++=+，其中22y x +=ρ，则曲面),(y x f z =在点)1,0(处的切平面方程为．解 切平面方程为0232=--+z y x ． 7. 直线111101-=-=-z y x 绕z 轴旋转的旋转曲面方程为．解 旋转曲面方程为1222=-+z y x ．8. 设L 为封闭曲线1||||=++y x x 的正向一周，则⎰=+-Ly y x x y x d )cos(d 22．解 原式0=．9. 设向量场k j i A 222232yz x z y x yz x --=，则其散度A div 在点)2,1,1(M 处沿方向}1,2,2{-=l 的方向导数=∂∂M |)(div A l．解 原式322=． 10. 设x x e x e y )1(2++=是二阶常系数线性微分方程x e y y y γβα=+'+''的一个特解，则=++222γβα．解14222=++γβα．二、（10分）设二元函数),(||),(y x y x y x f ϕ-=，其中),(y x ϕ在点)0,0(的一个邻域内连续．试证明函数),(y x f 在)0,0(点处可微的充分必要条件是0)0,0(=ϕ． .)0,0(),(.0),(||lim ,2||||||,),(||)0,0()0,0()0,0(),(.0)0,0(,0)0,0(,0)0,0()(.0)0,0(),0,0()0,(||lim ),0,0()0,(||lim ,)0,(||lim )0,0()0,(lim )0,0(.)0,0(),0,0(,)0,0(),()(220022222222220000点处可微在由定义所以又因为则可知若充分性故有且由于存在则点处可微在设必要性证y x f y x y x y x yx y y x x y x y x y x y x y x y x y f x f f y x f f f xx x x x x xx x x f x f f f f y x f y x y x y x x x x x x y x =+-≤+++≤+-+-=+'-'--='='==-===-='''→→→→→→-+ϕϕϕϕϕϕϕϕϕ三、（10分）设)(x f 在区间]1,1[-上三次可微，证明存在实数)1,1(-∈ξ，使得)0(2)1()1(6)(f f f f '---='''ξ．.)0(2)1()1(6)()].()([21)(),,()].()([61)0(2)1()1(,!3)(!2)0()0()0()1(,!3)(!2)0()0()0()1(21212121f f f f f f f f f f f f f f f f f f f f f f '---=''''''+'''='''∈'''+'''+'=--'''-''+'-=-'''+''+'+=ξξξξξξξξξξξ于是使得实数由导数的介值性知存在证四、（10分）设函数),(y x u ，),(y x v 在闭区域1:22≤+y x D 上有一阶连续偏导数，又=),(y x f i ),(y x v j ),(y x u +，=),(y x g i ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂y u x u j ⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+y v x v ，且在D 的边界上有1),(≡y x u ，y y x v ≡),(，求⎰⎰⋅Dσd g f ．.,1:π,d )cos sin sin (d d d d d )()(d ,)()(22π202正向解=+-=+-=+=+=⎪⎪⎭⎫⎝⎛∂∂-∂∂=∴∂∂-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-∂∂+∂∂=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=⎰⎰⎰⎰⎰⎰⎰∙∙y x L yy x y y uv x uv y uv x uv y uv x uv y v u y u v x v u x u v y v x v u y u x u v L L D Dθθθθσσg f g f 五、（10分）计算y x z x z y z y x d d d d d d 222++⎰⎰∑，其中14)1()1(:222=+-+-∑z y x )1(≥y ，取外侧．π.325π2π319π,319d )sin 32sin sin 41sin cos 41(d 4d sin )2sin sin sin cos 2(d d 2d )(2d )(2π,2d d .,14)1(:,,1:π022π0102π0π0220000=+=∴=++=++=+=++=-=-=-=≤+-=∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∑+∑∑∑∑+∑原式则原式左侧设解ϕϕϕθϕθθϕϕθϕθϕθrr r r v y x v z y x x z z x D y VVDπ.325π2π311π38,24)1(:π,611d )2(2πd d d d ,1,24)1(:π,34d )2(πd d d d π.2d )(2,d )(2π,2d d .,14)1(:,,1:2222221222202202200=++=∴-≤+-=-⋅⋅==≥-≤+-=-==+++=++=-=-=-=≤+-=∑⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰∑+∑∑∑∑+∑原式故原式则原式左侧设另解y y z x D y y y y x z x y v y y x x zy D x x x x z y xx v x v z y x v z y x x z z x D y y D Vx D V V VDyx六、（10分）设正项级数∑∞=1n na收敛，且和为S ．试求：（1）n na a a n n +++∞→ 212lim ；（2）∑∞=++++121)1(2n nn n na a a ．.1)1(22122)1(2)2(;02lim ,112)1(1121212121212112112112121++→∞---+++++++-+++=++++-+++=++++=-=+++∴-⋅-+++-=+++-=-++-+-+=+++n n n n n n n n n n n n n n n n n n n a n a n na a a n na a a n na a a n na a a n n na a a S S nna a a nn n S S S S n S S S S nS S S S S S S n na a a 解.)1(2)1(2,21111121112121S a a b n n na a a a b b n n na a a n na a a b n n n n n nn n n nn n ==+=++++∴+-=+++++++=∑∑∑∞=∞=+∞=++ 则记七、（10分）飞机在机场开始滑行着陆．在着陆时刻已失去垂直速度，水平速度为0v 米／秒．飞机与地面的摩擦系数为μ，且飞机运动时所受空气的阻力与速度的平方成正比，在水平方向的比例系数为x k 千克⋅秒2／米2，在垂直方向的比例系数为y k 千克⋅秒2／米2．设飞机的质量为m 千克，求飞机从着陆到停止所需的时间．).(arctan )()arctan(10).arctan(1)arctan(1).arctan(1,,0.)arctan(1,d d .0d d ,0)d d (d d .0,,.0)d d (d d ).(,,000002222222222秒时，当得代入初始条件积分得分离变量得即于是有根据题意知记由牛顿第二定律，有摩擦力垂直方向的阻力水平方向的阻力解v gm k k g k k mv BAABt v v BA ABv B AABt v BA ABC v v t C t v BAAB t BAv vB Av t vB t s A ts A g B mk k A g t s m k k t s R m g W v k R v k R y x y x yx y x y y x y x μμ-μμ-===-=∴===+-=-=+=++=++>μ=μ-==μ+μ-+-μ===以下两题乙组考生不做 八、（10分）证明1sin 是无理数．.1sin .,)12(2cos )1(,12,1|cos |).(cos )12(2)1(cos )12(2)1(])!12()1(!71!51!311[)!12()!12().12(cos )!12()1()!12()1(!71!51!311sin .,,1sin 1sin 11是无理数所以矛盾不可能是整数故然而两个整数之差仍是整数是整数知，由的展开式有根据是互素的正整数是有理数，则设证+->≤+-+-+--++-+--=->-+-+--++-+-==--n n n n n n n n n q p n q n n n q p x q p qpn n nn nn ξξξξξ九、（10分）在区间)2,0(π内，试比较函数)tan(sin x 与)sin(tan x 的大小，并证明你的结论．。

最新-2018年全国⾼中数学联赛试题及参考答案精品2018年全国⾼中数学联赛试题及参考答案试题⼀、选择题（本题满分36分，每⼩题6分）1、函数f (x)=log1/2(x2-2x-3)的单调递增区间是（）。

（A）（－∞,－1）（B）（－∞,1）（C）（1,＋∞）（D）（3, ＋∞）2、若实数x，y满⾜(x+5)2+(y-12)2=142，则x2+y2的最⼩值为（）。

（A）2 （B）1 （C）√3（D）√23、函数f(x)=x/1-2x-x/2（）（A）是偶函数但不是奇函数（B）是奇函数但不是偶函数（C）既是偶函数⼜是奇函数（D）既不是偶函数也不是奇函数4、直线x/4+y/3=1与椭圆x2/16+y2/9=1相交于A，B两点，该椭圆上点P，使得ΔPAB⾯积等于3，这样的点P共有（）。

（A）1个（B）2个（C）3个（D）4个5、已知两个实数集合A＝｛a1,a2,…,a100｝与B＝｛b1,b2,…,b50｝，若从A到B的映射f使得B中每个元素都有原象，且f(a1)≤f(a2)≤…≤f(a100)则这样的映射共有（）。

（A）C50100（B）C4899（C）C49100（D）C49996、由曲线x2=4y,x2=-4y,x=4,x=-4围成的图形绕y轴旋转⼀周所得旋转体的体积为V1；满⾜x2+y2≤16,x2+(y-2)2≥4,x2+(y+2)2≥4的点（x,y）组成的图形绕y轴旋转⼀周所得旋转体的体积为V2，则（）。

（A）V1=（1/2）V2 (B)V1=（2/3）V2 (C)V1=V2 (D)V1=2V2⼆、填空题（本题满分54分，每⼩题9分）7、已知复数Z1,Z2满⾜∣Z1∣＝2,∣Z2∣＝3,若它们所对应向量的夹⾓为60°,则∣(Z1＋Z2)/(Z1＋Z2)∣=。

8、将⼆项式（√x+1/（24√x））n的展开式按x的降幂排列，若前三项系数成等差数列，则该展开式中x的幂指数是整数的项共有个。

十八届数学竞赛试题及答案一、选择题（每题3分，共30分）1. 已知函数\( f(x) = 2x^2 - 3x + 1 \)，求\( f(2) \)的值。

A. 5B. 3C. 1D. -1答案：A2. 一个圆的半径为5，求其面积。

A. 25πB. 50πC. 75πD. 100π答案：B3. 以下哪个数是无理数？A. 0.33333...B. πC. √2D. 1/3答案：C4. 一个等差数列的首项是2，公差是3，求第10项的值。

A. 25B. 29C. 32D. 35答案：B5. 已知三角形ABC的三边长分别为3, 4, 5，求其面积。

A. 6B. 9C. 10D. 12答案：A6. 一个正方体的体积是27立方厘米，求其边长。

A. 3厘米B. 4厘米C. 5厘米D. 6厘米答案：A7. 以下哪个是二次方程的根？A. x = 2B. x = -2C. x = 3D. x = -3答案：C8. 一个直角三角形的两条直角边分别为3和4，求斜边的长度。

A. 5B. 6C. 7D. 8答案：A9. 已知\( \sin(30^\circ) = \frac{1}{2} \)，求\( \cos(30^\circ) \)的值。

A. √3/2B. √2/2C. 1/√2D. 1/2答案：A10. 一个数的平方根是4，求这个数。

A. 16B. 8C. 12D. 20答案：A二、填空题（每题2分，共20分）1. 圆的周长公式是 \( C = \pi d \)，其中 \( d \) 是直径。

如果\( d = 10 \)，则周长是 \( 30\pi \) 。

2. 一个数的立方根是 \( a \)，那么这个数是 \( a^3 \)。

3. 正弦函数在第一象限是正值。

4. 如果一个数列是等比数列，且首项 \( a = 2 \)，公比 \( r = 3 \)，那么第5项是 \( 162 \)。

5. 一个二次方程 \( ax^2 + bx + c = 0 \) 的判别式是 \( b^2 -4ac \)。